Artículo
Recibido: 13 de febrero de 2016/Aceptado: 29 de febrero de 2016
ENTORNOS, Vol. 29, No. 1, Junio 2016
Conflictos epistémicos al hacer transformaciones en las representaciones de una función
Fabián Meza Sarmiento
Universidad de Sucre, Colombia
famesa16051@hotmail.com [Link]
Tulio R. Amaya De Armas
Institución Educativa San Vicente de Paul &
Universidad de Sucre, Colombia
tuama1@hotmail.com [Link]
Resumen
En este trabajo se tuvo como objetivo analizar los conflictos epistémicos que tienen los estudiantes del grado once al realizar transformaciones con los elementos de una función. La muestra la constituyeron 85 estudiantes del grado once, con edades entre 16 y 18 años. La investigación se desarrolló en cuatro etapas: revisión documental, diseño, validación y aplicación de instrumentos y análisis e interpretación de resultados. Los resultados evidencian serias dificultades relacionadas con: el reconocimiento de los elementos de una función y sobre cómo éstos se relacionan y en el establecimiento de congruencias entre los elementos de dos o más representaciones. Los principales conflictos epistémicos que se han encontrado se relacionan con el reconocimiento de la función en contextos académicos, no reconocen las representaciones gráficas ni tabulares como representaciones de una función y por tanto pocos las usan como apoyo para dar sus respuestas, el uso indistinto de la letra como magnitud y como variable generalizada, la construcción de intervalos inapropiado donde se tenían en cuenta sólo uno de los límites de éstos, la construcción de gráficos apropiados, pero no convencionales, en los cuales se tomó al revés, la orientación del eje X y el reconocimiento sólo de la representación analítico aritmética y la analítico algebraica, como representaciones de una función.
Palabras clave: Conflictos epistémicos, registro figural, registro analítico, representación semiótica, función, conversión entre registros.
Epistemic conflicts when making transformations in the representations of a function
Abstract
This research was aimed to analyze epistemic conflicts that students have from eleventh grade to perform transformations with elements of a function. The sample comprised 85 eleventh grade students, aged between 16 and 18 years. The research was conducted in four stages: document review, design, validation and application of instruments and analysis and interpretation of results. The results show serious difficulties related with: The recognition of the elements of a function and how these relate and the establishment of congruences between the elements of two or more representations. The main epistemic conflicts that have been found are related to the recognition of the role in academic contexts, do not recognize the graphical representations neither tabular as representations of a function and therefore few use them as support to give their answers, the indistinct use of the letter as magnitude and as widespread Variable, the construction of appropriate graphics, but unconventional, where was taken reversely, the X axis orientation and the recognition alone of the arithmetic analytical representation and the algebraic, as representations of a function.
Introducción
En el área de matemáticas es común que los estudiantes presenten dificultades de comprensión en los procesos de aprendizaje de los conceptos estudiados. Estas dificultades se deben en parte, a que a diferencia de otras ciencias, el modo de acceso a los objetos matemáticos se hace únicamente por medio semiótico (Duval 2012), por lo que en la enseñanza y aprendizaje de las matemáticas se requiere necesariamente de mediadores semióticos, es decir, de acudir a las representaciones semióticas de un objeto matemático y estudiarlo analizando las congruencias e incongruencias entre los elementos de sus representaciones. En este sentido se acude a un sistema de signos como mediadores entre la mente y el concepto, lo que resulta ser determinante en la producción del conocimiento (Amaya, 2016). Proceso de adquisición del conocimiento denominado por Peirce (1974) noesis: objetivo fundamental de la semiótica. Noesis es todo acto cognitivo que facilite o permita la conceptualización de un objeto. Al respecto Duval (1999) considera que la noesis no es posible sin la semiosis, de donde puede inferirse que no es posible acceder a los objetos matemáticos sino es a través de sus representaciones semióticas; aspecto determinante de la importancia de estudiar las representaciones semióticas como único medio de acceso al conocimiento matemático.
Teniendo en cuenta lo anterior, para que se comprenda globalmente un concepto matemático, es necesario estudiarlo acudiendo a sus diferentes representaciones, ya que según Duval (2004), la comprensión integradora de un objeto matemático se basa en la coordinación de al menos dos de sus representaciones. Coordinación que se manifiesta por la rapidez y la espontaneidad con que se realicen transformaciones tipo conversión y/o tipo tratamiento entre dichas representaciones. Una transformación tipo conversión es el resultado de hacer un cambio de registro con los elementos de una representación de un objeto, es decir, es decodificar la representación en un registro de partida y recodificarla en otro registro, llamado registro auxiliar o de llegada. Una transformación tipo tratamiento es decodificar los elementos de una representación en un registro de partida y recodificarlo en el mismo registro.
El estudio de congruencias e incongruencias entre representaciones de un objeto matemático devela las homogeneidades y en algunos casos, serias heterogeneidades entre las representaciones en los registros que las contienen, es decir, hay elementos de las representaciones de un objeto que son ostensibles en varias de estas representaciones, cuando esto sucede los elementos presentes tanto en una como en otra representación se pueden comparar, a lo que se le llama establecer congruencias entre representaciones. Cuando existen estas congruencias se dice que las representaciones son homogéneas, en caso contrario las representaciones son heterogéneas. Esto condiciona la relación entre el objeto representado y su representante, ya que una representación en matemáticas no es posible hacerla al margen de un registro semiótico de representación, es decir, un tratamiento matemático solamente es posible realizarlo “utilizando las representaciones semióticas y no las representaciones mentales, por lo que de la conciencia de su uso, por parte de quien orienta los procesos de enseñanza y aprendizajes, va a depender en gran medida la comprensión conceptual” (Amaya, 2016, p. 30) en matemáticas.
Una de las grandes ventajas de usar conscientemente las representaciones semióticas es que se pueden reproducir en diferentes registros semióticos de representación. Asimismo, la forma de aproximación y “el tratamiento de los objetos matemáticos depende directamente del sistema de representación semiótico utilizado (…) Si se produce un cambio de registro semiótico también se modifica la representación semiótica, en cambio si se produce un cambio de representación semiótica no necesariamente cambia el registro” (Oviedo, Kanashiro, Bnzaquen y Gorrochategui, 2012, p.32). En lo anterior se pone de manifiesto que se pueden reproducir representaciones de un mismo objeto en dos o más registros semióticos: en cuyo caso, se cambia de registro y se transforma la representación; o hacer diferentes representaciones del objeto en un mismo registro: en este caso sólo se transforma la representación, conservándose el registro.
Uno de los grandes problemas en los procesos de enseñanza y aprendizaje de las matemáticas, en conceptos como funciones, es que generalmente los profesores se restringen a la utilización y manipulación de representaciones como la algebraica, y esto según Hitt (2003) produce limitaciones en la comprensión del concepto estudiado. Además, en general actividades como conectar diferentes representaciones de un objeto matemático no son considerada como fundamentales, por muchos profesores en la construcción del concepto (Amaya, Pino y Medina, 2016). Muchos de los conflictos que suelen surgir en el aprendizaje de conceptos matemáticos como el de función, se deben quizás a que no se tienen en cuenta estos detalles en sus procesos de enseñanza y aprendizaje. Lo cual lleva a pensar, que al estudiar la noción de función, enfatizando el aprendizaje en el análisis de un sólo registro de representación, puede llevar a la aparición de algunos conflictos epistémicos, los cuales según Godino (2009) son aquellos desajustes que se presentan en un proceso de instrucción que no es idóneo, y se da cuando el significado institucional implementado del objeto matemático que se estudia, no guarda fidelidad, ni con el significado institucional pretendido, ni con el de referencia. El significado de referencia corresponde a las convenciones establecidas sobre un objeto en las instituciones y comunidades matemáticas, y entre investigadores y educadores matemáticos.
El objeto matemático función ha sido estudiado por grandes pensadores que a través de grandes esfuerzos han logrado un desarrollo histórico de más de 2000 años, a través de los cuales ha sido objeto de diversas acepciones y generalizaciones (Parra y Pino-Fan, 2016). Entre las configuraciones epistémicas de una función y de las relaciones funcionales consideradas a través de su desarrollo histórico están:
La función como correspondencia
En las antiguas civilizaciones de Egipto, Mesopotamia, China e India se encontraron evidencias como marcas sencillas en restos óseos que conllevaron a la idea de contar, generando una correspondencia entre un conjunto dado de objetos y una secuencia de números para contar, es decir, se establecía una correspondencia entre objetos físicos con la cantidad de estos objetos. Teniendo en cuenta este planteamiento, la noción de función tiene sus raíces en el desarrollo del concepto de número (Sastre, Rey y Boubée, 2008). En esta configuración de la noción función también se registraron tablas y papiros con información relevante sobre los conocimientos matemáticos de los pueblos.
La función como relación entre magnitudes
En civilizaciones como la griega y la babilónica se asociaban elementos de dos conjuntos. Se establecían relaciones entre elementos de dichos conjuntos, registrados en tablas de cálculo, donde se evidencian serios intentos por aritmetizar observaciones muy difíciles de medir, y además, no se limitaban a una simple tabulación de datos empíricos, sino que usaron interpolaciones y extrapolaciones como buscando patrones de regularidad y de crecimiento (Ruiz, 1994). Y aunque no lograron concebir el objeto función, estos estudios sobre relaciones entre magnitudes variables, si pueden considerarse como los primeros antecedentes aportados por las culturas griega y la babilónica al desarrollo del objeto matemático función (Sastre, Rey y Boubée, 2008).
La función como representación gráfica
Desde la edad media, los árabes produjeron importantes aportaciones, entre ellas la introducción de la aritmética y fueron ellos quienes sentaron las bases del álgebra, estudiaron fenómenos naturales como: luz, calor, densidad, distancia, velocidad y movimientos uniformemente acelerados (Parra y Pino-Fan, 2016). Basados en estos estudios asociaron la noción de función al cambio y al movimiento, o mediante representaciones gráficas, y establecieron implícitamente, nociones como cantidades, variables dependientes e independientes. Pero todavía no lograron asociar el objeto matemático función a una expresión algebraica.
La función como expresión analítica
El desarrollo de esta parte de la teoría de las funciones se fundamenta en tres aspectos: 1) el marcado crecimiento de los cálculos matemáticos, 2) la aparición y uso de la letra como variable, esto es, la creación del álgebra simbólico-literal, y 3) la extensión del concepto de número al de números reales. Con los estudios de Fermat y de Descartes se dio paso al descubrimiento y uso de representaciones analíticas y comenzó a formalizarse la geometría analítica y se empieza a consolidar la idea de variable algebraica (Ruiz, 1994).
La función como correspondencia arbitraria
Es Dirichlet el primero en dar a conocer un ejemplo explícito de una función sin acudir a su representación analítica ni a su representación gráfica. Fue el primer matemático en considerar a una función como una correspondencia arbitraria (Parra y Pino-Fan, 2016), y además, dio un ejemplo de una función que es discontinua en todas partes, considerándola en el mismo sentido que se le da actualmente. Fue a partir de los trabajos de Dirichlet que al concepto matemático función se le asocian significados sin considerar su representación algebraica (Sastre, Rey y Boubée, 2008). A partir de entonces, se comienzan a dar definiciones muy parecidas a las conocidas actualmente; se pone como ejemplo una dada por Riemann en el año 1858: “Se dirá que y es función de x si a todo valor bien determinado de x corresponde un valor bien determinado de y cualquiera que sea la forma de la relación que una a x y a y” (Ruiz, 1994, p. 183).
La función a partir de la Teoría de Conjuntos
En su desarrollo histórico, puede apreciarse que a medida que se consolida el concepto de función -al igual que la matemática en generalse va haciendo cada vez más abstracto, dando origen a definiciones muy teóricas de tipo conjuntistas, que nacieron en el seno del álgebra abstracta y de la topología. Un ejemplo de estas definiciones es la dada por el grupo Bourbaki:
Sean E y F dos conjuntos, que pueden o no ser distintos. Una relación entre un elemento variable x de E y un elemento variable y de F, se llama relación funcional en y, si para todo x en E, existe un único y en F el cual está en la relación dada con x. Damos el nombre de función a la operación que, de esta forma, asocia cada elemento x en E con el elemento y en F que está en relación con x, se dice que y es el valor de la función en el elemento x, y se dice que la función está definida por la relación dada. Dos relaciones funcionales equivalentes determinan la misma función (Sastre, Rey y Boubée, 2008, p. 152).
Esta definición guarda muchos elementos de la dada por Dirichlet, es decir, el tratamiento que se da a la función es como una correspondencia entre dos conjuntos, pero incorpora otra tipología de signos: 𝐹 (gráfica de la función), 𝑓 (la función) y (𝑥) (la imagen de la función). Bourbaki establece relaciones de los signos 𝑓(𝑥) y 𝑥 con elementos del plano cartesiano, donde 𝑥 corresponde a las unidades sobre el eje horizontal y 𝑓(𝑥) su imagen siendo ésta una expresión numérica o algebraica y (𝑥, 𝑓(𝑥)) puntos del plano, entendidos como el valor o posición que puede ir tomando el punto.
“El surgimiento de 𝑓 volcó a entender a 𝑓(𝑥) como un objeto con el cual se puede operar, analizar, manipular, pero principalmente con el que se podrá determinar a la función, es decir 𝑓, ya que estudiando estas imágenes es que se puede caracterizar a la función” (Parra y Pino-Fan, 2016, p. 22).
El objeto matemático función es uno de los que muestra mayor facilidad en la producción de sus representaciones, por la cantidad de registros en los que es posible producirlos (Hitt y Morasse, 2009). Entre los registros más usuales para representar funciones están:
El del lenguaje materno o coloquial el cual es muy adecuado para la presentación de relaciones funcionales, a través de las que se describen situaciones del contexto sociocultural, que involucra el uso de una función, permitiendo el tránsito a otros registros semióticos de representación. Es ideal para enunciar situaciones funcionales, como la siguiente: una persona trabaja en un lavadero de autos y tiene un sueldo compuesto por un salario básico mensual de 40 pesos, más un salario adicional de 5 pesos por cada auto que lave. El registro de representación analítica, el cual está relacionado con la modelación y con el pensamiento variacional y las estructuras algebraicas. Para el ejemplo presentado en el registro coloquial, una representación algebraica sería f(x) = 5x + 40, o un polinomio aritmético resultado de indagar el salario del trabajador cuando lava 352 autos en el mes, el polinomio aritmético sería f(352) = 5(352) + 40, o como una ecuación (5x + 40 = 1800), al conocer el salario mensual del trabajador en un mes determinado y a partir de ahí encontrar el número de autos lavados por él en el mes; también se puede representar como una secuencia (40, 80, 120, 160,…). El registro de representación gráfico que consiste en la representación en un plano cartesiano de una información específica correspondiente a un conjunto de puntos que determinan la gráfica. La graficación está muy relacionada con la capacidad de visualización y con el pensamiento geométrico; en ella se conjuga la interacción de dos estructuras en mutua dependencia: el fondo y la forma (Acuña, 2001). El registro de representación figural que es una representación icónica correspondiente a una figura o dibujo de una situación real, en la que se involucra el concepto de función y la que además permite el tránsito a otros registros de representación de esa función. El registro sagital corresponde a una relación de correspondencia entre dos conjuntos. Cada conjunto está representado en un óvalo o conjunto inicial (conjunto de partida) y cada uno de sus elementos se hace corresponder con un solo elemento del conjunto de llegada. El registro de representación tabular se parte de una tabla, en la que se ubican las entradas ya sean en las filas o en las columnas, de tal forma que el número de columnas (o filas según sea el orden), corresponda al total de cantidades que intervienen en la situación, que vienen a ser los elementos que constituyen la función. Y el registro de representación fenomenológico propuesto por Amaya y Medina (2013), conformado por factores sociales y culturales ajustados a la clase de matemáticas. En el intervienen tanto factores endógenos como exógenos, que permiten contextualizar elementos de la disciplina hasta bajarlos a un lugar asequible para el aprendiz.
Son las representaciones producidas en el registro fenomenológico las que permiten asignar significado y sentido a los conceptos matemáticos estudiados, al comparar sus elementos con los de otras representaciones del mismo objeto. Y todas las representaciones en su conjunto, permiten un estudio a profundidad de las funciones, permitiendo que el estudiante tenga un mejor acercamiento y apropiación de dicho concepto.
Para ilustrar lo anterior, considérese el caso en que se cortan cuadraditos de lado l de las esquinas de una hoja de papel tamaño carta de dimensiones 27.8 cm por 21,7 cm aproximadamente, para formar una caja sin tapa, de la cual se pide obtener su área lateral. El enunciado anterior corresponde a una situación funcional, dada en un registro coloquial, que corresponde a la situación utilizada en el cuestionario del que aquí se reportan los resultados. Al hacer una conversión al registro algebraico, se obtiene la representación algebraica A(l) = 603.26 - 4l2, si se hace una nueva conversión al registro gráfico, se puede obtener algunas de las representaciones mostradas en la figura 1 (de la figura 1a, la parte que está en rojo), si se hace una conversión al registro tabular, se obtiene la tabla mostrada en la figura 2a y al registro figural se obtiene la cajita mostrada en la figura 2b. En todas las conversiones se cambió de registro y la representación automáticamente también cambió. Las gráficas de las figuras 1b y 1c se obtuvieron por transformaciones tipo tratamiento, en este caso sólo se modificó la representación, el registro siguió siendo el gráfico. Sin embargo, sólo las gráficas mostradas en las figuras 1a (la parte que está en rojo), 1b y 1c, son representaciones de A(l), ya que la figura 1a en su totalidad representa es la función f(x) = 603.26 - 4x2. Hay una diferencia bien marcada entre A(l) y f(x), el dominio de A(l) son los valores de ℓ entre 0 y 10.9, mientras que el dominio de f(x) es el conjunto de los números reales. De forma similar, el rango de A(l) son los valores de A entre 0 y 603.26, mientras que el rango de f(x) es el conjunto de números reales desde - ∞ a 603.26. Por otro lado, la gráfica mostrada en la figura 1c es una construcción apropiada, no convencional, para esta representación, donde los valores del eje de las abscisas se tomaron en sentido contrario a lo convencionalmente aceptado, es decir, corresponde a lo convencionalmente aceptado como A(-l). Estos desajustes son los que en la mayoría de los casos, producen los conflictos epistémicos.
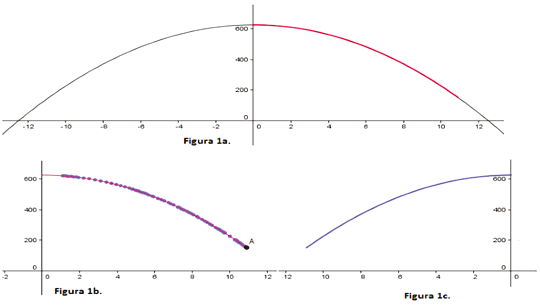
El establecimiento de congruencias entre los elementos de las representaciones de una función se logra al emparejar los elementos ostensibles tanto en una, como en otras representaciones. Para el caso, el punto P(4, 561.66), que es un elemento de una representación cartesiana, es equivalente a la segunda entrada que se muestra en la tabla (Figura 2a), pero también es equivalente al punto, que en la gráfica, marca estas coordenadas y a la caja formada cuando se recortaron cuadraditos de lado 4 cm en las esquinas de la hoja, y en general, cada caja con sus elementos corresponde a un punto de la gráfica. En la representación algebraica del área lateral: A(l)=603.26-4l2, se puede interpretar, que el área lateral de la caja es equivalente al área total de la hoja quitándole los cuatro cuadraditos de las esquinas de la hoja. También se evidencian incongruencias entre estas representaciones, por ejemplo, la concavidad ostensible en la representación gráfica, no es apreciable en ninguna otra representación. Estos aspectos determinan la homogeneidad o heterogeneidad entre las representaciones.

Ante este hecho, se planteó la necesidad de analizar la presencia de algunos conflictos epistémicos en el aprendizaje de las funciones en estudiantes del grado once, por lo cual surge la siguiente pregunta ¿qué conflictos epistémicos presentan los estudiantes del grado once al hacer transformaciones tipo conversión o tipo tratamiento entre registros de representación de una función? Para responder dicho interrogante, se estableció como objetivo general de investigación, “analizar los conflictos epistémicos que tienen los estudiantes del grado once al realizar transformaciones con los elementos de una función”, buscando así identificar y clasificar dichos conflictos, para luego buscar las posibles causas que favorecen de alguna forma la existencia de los mismos.
Metodología
Este trabajo de investigación es de tipo cualitativo, se hizo un estudio descriptivo de casos (Servan y Servan, 2010). Se hace un abordaje de las funciones desde la teoría de Duval (1999, 2004, 2012). El trabajo fue realizado durante el primer semestre del 2016. Se aplicaron tres cuestionarios, pero en este artículo se comparten los resultados de sólo uno de ellos. Se establecieron como unidades de análisis los resultados de las resoluciones por parte de 85 estudiantes del grado once a un cuestionario, al que se les enfrentó, con situaciones del contexto sociocultural, que involucran funciones. En el cuestionario se les pide hacer transformaciones tipo conversión y tipo tratamiento con los elementos de las funciones involucradas. Se les pide además, asociar cada elemento que identifiquen en una representación con su equivalente en otras representaciones y relacionarlo con los elementos correspondientes del contexto sociocultural.
Las categorías de análisis que se establecieron en los tres instrumentos aplicados son los siguientes: identificación y uso de los elementos de una función, identificación y uso de los intervalos de variación de una función, determinación de los máximos y mínimos de una función, modelación matemática de una situación funcional e identificación y uso de un patrón de regularidad y de crecimiento de una función.
El instrumento que se le aplicó a los estudiantes consistió en lo siguiente: se les entregó una hoja de papel tamaño carta (de dimensiones aproximadas de 21.7 cm×27.8 cm) con la instrucción de construir una caja sin tapa, al quitar en las esquinas cuadraditos de lado l. Luego responder las cuestiones que se pueden apreciar en la siguiente tabla 1:
Tabla 1. Categorías de análisis y cuestiones planteadas a los estudiantes en el cuestionario.
| N° | Categorías de análisis | Cuestiones planteadas |
| 1 | Identificación y uso de los elementos de una función | ¿En qué intervalos es cóncava hacia arriba y hacia abajo cada
una de las dos funciones? ¿Qué cantidades intervienen en la situación, cuales varían y cuales permanecen fijas? |
| 2 | Identificación y uso de los intervalos de variación de una función | ¿Cuál es el dominio y cuál es el rango de la función volumen y área lateral? |
| 3 | Determinación de los máximos y mínimos de una función | ¿Cuáles son los puntos máximos y cuáles son los puntos mínimos de la función volumen y área lateral? |
| 4 | Modelación matemáticamente de una situación funcional | - Encuentra una expresión matemática que permita modelar la
situación tanto para el área lateral y el volumen. - Realiza la gráfica tanto para el área lateral como para el volumen de todas las cajas. |
| 5 | Identificación y uso de un patrón de regularidad y de crecimiento de una función | ¿En qué intervalos crece y en qué intervalo decrecen la función volumen y la función área lateral? |
En cada ítem estaba inmerso algún elemento de la función, con el propósito de que el estudiante lo identificara en uno u otro registro haciendo la conversión y/o el tratamiento y pusiera en paralelo los elementos que identificara en cada representación. Por ejemplo, el estudiante debía deducir que al modelar la situación por medio de una representación algebraica o una gráfica, para establecer congruencias entre las representaciones se debía restringir el dominio, correspondiente a las magnitudes presentes en la situación, en lugar de utilizar la letra como variable generalizada.
Se utilizaron tres tipos de técnicas de recolección de datos: cuestionarios escritos con preguntas abiertas, entrevistas semiestructuradas y observación participante. Mientras los estudiantes desarrollaban el cuestionario se observaba minuciosamente lo que hacían y se resolvía al instante cualquier duda con respecto a la prueba. La entrevista estaba centrada en las preguntas del cuestionario, las cuales sólo se les hizo a aquellos estudiantes cuyas respuestas planteadas resultaron interesantes o aquellos cuyas respuestas generaban ciertas dudas al ser interpretadas.
Para el análisis de las respuestas dadas por los estudiantes, se siguieron técnicas de análisis de contenido (Bernárdez, 1995). Los resultados fueron agrupados de acuerdo al conflicto epistémico identificado, con las principales dificultades asociadas y en algunos casos fueron ilustrados con manuscritos de los estudiantes al resolver las cuestiones por las que se les indagaron, y finalmente la descripción cualitativa detallada de las características de cada conflicto.
Resultados y discusión
El no reconocimiento de la función en contextos académicos
El primer conflicto que presentaron los estudiantes al enfrentárseles a la actividad fue no reconocer lo matemático de ésta, es decir, identificar y usar el concepto de función, en la situación funcional, para responder las cuestiones por las que se les indagaron. El conflicto se manifestó desde el primer momento que se les pidió construir la caja y encontrar, tanto su área lateral, como su volumen: seguían desarrollando la actividad pero desde el punto de vista artístico, les costó relacionar volumen y área lateral de la caja con el objeto matemático función. Una de las principales causas de esta dificultad fue poder relacionar la dimensión del lado del cuadradito y volumen de su caja, con un punto específico (l, V(l)), porque no lo veían como un punto que podían ir variando para construir una tabla, hacer una secuencia o realizar una gráfica. Confundían crecimiento/decrecimiento con concavidad, lo que pudo ocasionar que no identificaran el punto de inflexión en la representación gráfica del volumen de la caja; en el manuscrito del estudiante E22 se ponen de manifiesto algunos de estos aspectos.

Entre las principales dificultades originadas por este conflicto se pueden destacar:
Incluían valores en la tabla que no corresponden a la situación funcional. Cuando se les preguntó por las cantidades que intervienen en la situación el 61,7% sólo reconocen tres cantidades: el largo, el ancho y el valor del cuadrito. Desconociendo otras cantidades como el área lateral y el volumen de la caja. El 81,2% reconocen algunas de las cantidades que intervienen en la situación como son el largo, el ancho y el valor de “x”, y afirman que permanecen fijas, pero parece que hacen referencia es al largo y al ancho de la hoja, no al largo y ancho de la caja, como se muestra en la solución dada por el estudiante E22 mostrada en la figura 3. El 8,3% afirma que en la función volumen todas las cantidades varían y ninguna se mantiene fija, sin especificar cuáles son. El 8,3% afirma que la cantidad que se mantiene fija en la función área lateral es el lado del cuadrito cuando toma ciertos valores, como si variar y mantenerse fijo fuera lo mismo. El 8,3% no reconoce el largo, el ancho de la caja como cantidades que varían. El 8,3% afirma que el tamaño de la hoja permanece fija, cuando para formar la caja se necesita cortar los cuadritos de las esquinas. Se evidencia en estos estudiantes una descompensación al identificar y luego relacionar los elementos de una representación en uno o varios registros y relacionarlos con elementos del contexto sociocultural, lo que podría impedir en ellos el desarrollo del pensamiento variacional que según Hitt (2003) es indispensable para el acceso al cálculo.
Lo interesante de este asunto es que en contextos sociales no académicos se les ven usar con naturalidad las funciones, es decir, usan secuencias y con ellas pueden predecir resultados. Lo complicado según ellos es “matematizar los resultados”, queriendo decir –algebrizarlos, porque como se muestra más adelante, la representación algebraica es la única que reconocen como representación de una función.
Reconocer sólo la representación analítico aritmética y algebraica, como representación de una función
El conflicto de reconocer sólo la representación algebraica como representación de una función, consiste en que para los estudiantes solamente se habla de función al utilizar su representación algebraica y aunque hubieran producido otras representaciones para las funciones involucradas, no las usaron como apoyo para dar sus respuestas, reforzando lo reportado por Amaya y Medina (2013) al trabajar con situaciones similares a las aquí presentadas y al indagar por cuestiones muy afines a las planteadas en este trabajo.
Este conflicto se manifestó al indagárseles a los estudiantes por el crecimiento o decrecimiento de las funciones área lateral y volumen de la caja, éstos debían tomar valores del dominio de la función escogida y resolver sucesivos polinomios aritméticos para analizar la secuencia de puntos, de donde derivaban sus respuestas, sin tener en cuenta que ya habían realizado un registro tabular y otro gráfico, de donde hubiera sido mucho más fácil deducir respuestas apropiadas. Sin embargo en esta práctica, los estudiantes reprodujeron representaciones como la tabular, la gráfica, la analítico aritmética (polinomios aritméticos, secuencias y pares ordenados) y la analítico algebraica, sin embargo, en concordancia con lo reportado por Parra y Pino-Fan (2016), solo reconocen y usan representaciones como la analítico algebraica y la analítico aritmética para apoyar sus respuestas.
Uso indistinto de la letra como magnitud y como variable generalizada
El uso indistinto de la letra como magnitud o como variable generalizada (Font, 2011) es un conflicto consistente en utilizar en lugar de A(l) o V(ℓ), g(x) y f(x) respectivamente. Hay que hacer claridad en que no son funciones equivalentes, mientras que A(ℓ) y V(ℓ) representan las relaciones funcionales correspondientes al área lateral y al volumen de la caja, planteadas en la situación, y cuyos respectivos dominios van desde 0 hasta 10.9, las funciones g(x) y f(x) representan cualquier función matemática con esas características, cuyos dominios van desde - ∞ hasta + ∞, y sus respectivos rangos también son diferentes, por lo tanto no son funciones equivalentes.
El conflicto se hizo evidente en los estudiantes al expresar los intervalos de variación de las dos funciones: no pusieron restricciones en el dominio ni en el rango de las dos funciones, el cual corresponde según el contexto de la situación, tanto para la función área lateral como para la función volumen a {x ∈ R / 0 <x <10.9}; realizaron las representaciones gráficas con valores mayores a 10.9 para el dominio. En la figura 4 se muestran las representaciones gráficas tanto para el área (figura 4a), como para el volumen (figura 4b). La parte de cada gráfica que aparece en rojo, corresponde a la representación de la situación funcional planteada en la situación, mientras que las representaciones gráficas mostradas en las figuras 4a y 4b en su totalidad, representan las funciones matemáticas con variables generalizadas g(x) y f(x) respectivamente.
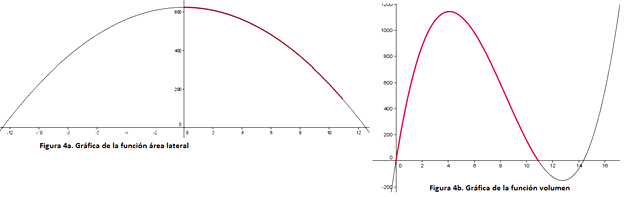
El que se use la letra, indistintamente como magnitud y como variable generalizada es algo que no sorprende, ya que al observar a los docentes de matemáticas y los de física, estos en sus orientaciones no hacen ninguna referencia a la letra como magnitud, al trabajar con relaciones funcionales (Font, 2011). Los docente en el mejor de los casos, mencionan las restricciones del dominio y del rango para las relaciones funcionales, sin analizarlas frente al correspondiente dominio y rango de la función generalizada correspondiente.
Construcción de gráficas no convencionales
Construyeron gráficas apropiadas pero no convencionales para modelar gráficamente la situación funcional, tanto para el área lateral A(l), como para el volumen V(l) de la caja. En este sentido, los significados institucionales y locales entran en conflicto con otros significados institucionales de referencia porque las convenciones establecidas en las comunidades de matemáticos y de educadores matemáticos entran a chocar con las creencias o conocimientos previos de los estudiantes. Una vez detectado, por los propios estudiantes, este tipo de conflicto funcionó como detonador epistémico, en el sentido de Hernández (1996), pues logró comprometer la voluntad de los estudiantes, estimulándolos a resolver la situación. En la figura 5 se muestra la gráfica realizada por el estudiante E5, quien al construir V(l) terminó realizando la representación gráfica de V(-l).

Pasó algo bien interesante, cuando en los grupos de discusión E5 mostró su gráfica, los demás compañeros estuvieron de acuerdo en que estaba mala, sin embargo, cuando se les pidió explicar por qué estaba mala, no pudieron dar razones de peso que justificaran su decisión. Luego de un conversatorio bastante prolongado E12 manifestó que “está mala porque el eje X está al revés de como normalmente se hace”. En el argumento presentado por E12 se evidencia su reconocimiento de convenciones institucionalizadas respecto de la graficación de funciones, lo que puso en evidencia el conflicto y mandó a E5 y a sus otros seis compañeros que dieron la misma respuesta, a reconstruir su gráfica. Otra dificultad que se presentó en esta situación fue al pedírseles a los estudiantes la representación algebraica que debió haber utilizado E5 y sus otros compañeros que dieron esta respuesta, para construir su gráfica; los estudiantes no pudieron dar con esta respuesta.
Construcción de intervalos inapropiados
La construcción de intervalos inapropiados consistió en una combinación del uso indistinto de la letra como magnitud o como variable generalizada y una inadecuada construcción de los intervalos de variación de las funciones área lateral y volumen de la caja. Por ejemplo expresaban el domino de las funciones área lateral y volumen de la caja mediante intervalos por comprensión, cerrados donde incluían el cero sin tener presente el contexto de la situación; decían “la función volumen crece de cero a 1143.08, sin utilizar la abscisa al determinar cada punto. La letra que utiliza como abscisa para expresar el dominio de ambas funciones, es la misma que usa para expresar el rango.
Al expresar el rango de la función área lateral, el intervalo lo expresa usando como límite inferior la abscisa, y como límite superior la ordenada. Sin tener en cuenta que si se está hablando del rango, tanto el límite inferior como el superior del intervalo deben ser ordenadas. No incluyen todos los valores que pertenecen al dominio de la función área lateral y la función volumen en el contexto de la situación. En términos generales, al referirse a un punto específico sólo mencionan la ordenada, como se muestra en la figura 6. Estos hallazgos refuerzan lo reportado por Amaya (2016), quien manifiesta que algunos aspectos de este tipo de conflictos no había sido reportado antes y que parecen ser bien comunes entre los estudiantes al trabajar con funciones.

Conclusiones
Los resultados preliminares de esta investigación permiten concluir que, aunque los estudiantes participantes ya habían trabajado funciones en varios cursos anteriores, se observaron serios conflictos al hacer conversiones y tratamientos entre los registros que se les pidió hacer. Los principales conflictos epistémicos que se han encontrado se relacionan con el reconocimiento de la función en contextos académicos, es decir, las funciones que se les plantean en las situaciones no son reconocidas como tal por los participantes en el estudio, no reconocen las representaciones gráficas ni tabulares como representaciones de una función y por tanto pocos las usan como apoyo para dar sus respuestas (Amaya y Medina, 2013), utilizan indistintamente la letra como magnitud y como variable generalizada, construyeron intervalos inapropiados donde se tenían en cuenta sólo uno de los límites de éstos, construcción de gráficos apropiados, pero no convencionales, en los cuales se tomó al revés, la orientación del eje X y reconocían sólo la representación analítico aritmética y la analítico algebraica, como representaciones de una función.
Referencias
Acuña, C. (2001). Concepciones en graficación, el orden entre las coordenadas de los puntos del plano cartesiano. Revista Latinoamericana de Investigación en Matemática Educativa. Vol 4. México. Pp. 203-217.
Amaya, T. (2016). Evaluación de la faceta epistémica de los conocimientos didáctico-matemáticos de futuros profesores de matemáticas al hacer transformaciones de las representaciones de una función. (Tesis doctoral). Madrid: Uned.
Amaya, T., Pino-Fan, L. & Medina, A. (2016). Evaluación del conocimiento de futuros profesores de matemáticas sobre las transformaciones de las representaciones de una función. Revista Educación Matemática, (Artículo en revisión).
Bernárdez, E. (1995). El papel del léxico en la organización textual. Madrid: Universidad Complutense de Madrid.
Duval, R. (1999). Semiosis y pensamiento humano. Cali, Colombia: Universidad del Valle.
Duval, R. (2004). Los problemas fundamentales en el aprendizaje de las matemáticas y las formas superiores del conocimiento. Cali, Colombia: Universidad del Valle.
Duval, R. (2012). Lo esencial de los procesos cognitivos de comprensión en matemáticas: los registros de representación semiótica. En U. Malaspina (Coord.). Resúmenes del VI Coloquio Internacional de Didáctica de las Matemáticas: avances y desafíos actuales (pp.14-17). Lima: Pontificia Universidad Católica del Perú.
Gatica, N., A. Maz-Machado, G. May, C. Cosci, G. Echevarría y J. Renaudo (2010), “Un acercamiento a la idea de continuidad de funciones en estudiantes de Ciencias Económicas”, Unión, Revista Iberoamericana de Educación Matemática, núm. 22, pp. 121- 131.
Godino, J. (2009). Categorías de Análisis de los conocimientos del Profesor de Matemáticas. Revista iberoamericana de educación matemática, (20), 13-31.
Font, V. (2011). Las funciones y la competencia disciplinar en la formación docente matemática. UNO. Revista de Didáctica de las Matemáticas, 56, 86-94.
Hernández, V. (1996). Algunas conjeturas sobre la noción de problema, lingüística y educación matemática y las perspectivas del uso de tecnología. Recuperado el 20 de junio de 2016, del sitio web. http://fractus.uson.mx/Papers/Varios/Cap1.html [Link]
Hitt, F. (2003). Una Reflexión Sobre la Construcción de Conceptos Matemáticos en Ambientes con Tecnología. Boletín de la Asociación Matemática Venezolana, 10(2), 213-223.
Hitt, F. & Morasse, C. (2009). “Pensamiento numérico-algebraico avanzado: construyendo el concepto de covariación como preludio al concepto de función”, Electronic Journal of Research in Educational Psychology, vol. 7, núm. 17, pp. 243-260.
Oviedo, L. Kanashiro, A. Bnzaquen, M. & Gorrochategui, M. (2012). Los registros semióticos de representación en matemática. Revista Aula Universitaria (13), 29-36.
Parra, Y., & Pino-Fan, L. (2016). Significados pretendidos por el currículo de matemáticas chileno sobre la noción de función. Artículo en revisión.
Peirce, Ch. (1974). La ciencia de la semiótica. Buenos Aires: Ediciones Nueva Visión.
Ruiz, L. (1994). Concepciones de los alumnos de secundaria sobre la noción de función. Análisis epistemológico y didáctico. Tesis doctoral. Granada: Universidad de Granada.
Sastre, P., Rey, G., & Boubée, C. (2008). El concepto de función a través de la historia. Revista Iberoamericana de Educación Matemática, 16, 141-155. doi: 1815-0640.