Artículo
Recibido el 15 de septiembre de 2017/ Aprobado el 31 de octubre de 2017
ENTORNOS, Vol. 30, No. 2, Noviembre 2017
Construcción del conjunto ternario de cantor a través de la dinámica simbólica
Luis Arturo Polania Quiza
Universidad Surcolombiana, Colombia
lapola@usco.edu.co [Link]
Anderson Penagos Rojas
anderfelep_44@hotmail.com [Link]
Resumen
Se presenta y utiliza en el siguiente artículo, un grupo de propiedades que contribuyen a la construcción del Conjunto Ternario de Cantor acudiendo a la dinámica simbólica, cuya función es caracterizar las estructuras de las órbitas de un sistema dinámico dado por medio de una sucesión de símbolos. Siendo el Conjunto Ternario de Cantor, en términos topológicos, un conjunto compacto, infinito y perfecto, no denso en cualquier intervalo.
Palabras clave: Compacto, topología, órbitas, Conjunto Ternario de Cantor sucesión.
Construction of the Cantor ternary set through symbolic dynamics
Abstract
It is presented and used in the following article, a group of properties that contribute to the construction of the Cantor Terrestrial Assembly by resorting to symbolic dynamics, whose function is to characterize the structures of the orbits of a given dynamic system by means of a succession of symbols. Being the Terrestrial Set of Cantor, in topological terms, a compact, infinite and perfect set, not dense in any interval.
Keywords: Compact, topology, orbits, Terrestrial Set of Cantor succession.
Introducción
La teoría de los sistemas dinámicos consiste en descubrir y describir las características de la acción de una transformación sobre un espacio. Dado un espacio de puntos y una transformación del espacio en sí mismo, a la dinámica le concierne averiguar cómo se mueven los puntos al aplicar sucesivamente la transformación y, en resumidas cuentas, cuál es el destina que esta les depara. Por tanto, la dinámica simbólica, que nace con la teoría de los sistemas dinámicos topológicos, desarrollada por Morse y Hedlung (1938), es una herramienta muy útil en el estudio de los sistemas dinámicos, especialmente en el estudio del comportamiento caótico, describiendo las órbitas de esta dinámica. Su ventaja reside en el hecho de que esta técnica reduce, un complicado sistema dinámico, en un conjunto de secuencias de símbolos; lo cual simplifica el trabajo para resultados posteriores de dicho sistema.
Por otra parte, el Conjunto de Cantor, en particular, no fue construido por primera vez por Georg Cantor, sin embargo, fue él quien lo describió de tal manera que resolvió algunos problemas que se habían planteado en el marco de la naciente topología. Durante los años 1879-1884, Cantor escribió una serie de ensayos, donde introduce el conjunto que viene a ser conocido como el Conjunto Ternario de Cantor. Él, en estos ensayos, hace notar que este conjunto es infinito y perfecto, con la propiedad de que no es denso en cualquier intervalo, a pesar de qué tan pequeño se tome el intervalo. Este conjunto, aparece como contraejemplo en diversas áreas de las matemáticas, como es el caso de Análisis Numéricos, Ecuaciones Diferenciales, Sistemas Dinámicos y hasta en Estadística. Sería muy difícil que un solo artículo, abarcara todos estos tópicos, pues como es posible notar, corresponden a áreas muy diferentes de las matemáticas.
En particular, el siguiente escrito, se enfocó más hacia el estudio de los Sistemas Dinámicos, a través de la utilidad de la dinámica simbólica, en el estudio de esta área. Por lo cual, se construirá el Conjunto Ternario de Cantor, por medio de sucesiones de símbolos, donde su construcción clásica, se basa en suprimir los tercios medios de los intervalos que van quedando, a partir del intervalo [0,1].
Dinámica Simbólica
La dinámica simbólica, es de las herramientas más útiles para el análisis del comportamiento caótico de los sistemas dinámicos. Consiste en caracterizar la estructura de las órbitas de un sistema dinámico, por medio de una sucesión de símbolos.
Ejemplo 1, el sistema dinámico asociado a la función tienda campaña
,
definida en el intervalo [0,1]. Como se verá, el comportamiento de las órbitas que no se escapan de este intervalo, es exactamente el conjunto de Cantor. Se denota a Λ, el conjunto de los puntos en I. En el ejemplo 1, I = [0,1] y Λ= C, donde C es el conjunto de Cantor.
Para entender la dinámica de f en I, dado x0 ∈ C, toda órbita de x0 se encuentra en I. Es posible asociar una sucesión infinita S(x0)=(0.s1s2s3…), como se verá más adelante, que consiste de 0, 1, y 2. La sucesión S(x0) es llamada el itinerario de x0.
Ahora, el conjunto ∑ (el espacio sucesión), consiste en todas las sucesiones posibles de símbolos, como 0 y 1, es decir, que los elementos de ⅀ son sucesiones, no números. Por ejemplo, (0000…), (010101…), (101010…) y (1111…), todos serían elementos distintos de ∑.
En el ejemplo 1, como se verá más adelante,
∑ = {(0.s1s2 ...): si = 0,1,o,2}.
Para determinar, que tan lejos se encuentran los puntos en sumatoria. Sean s = (s0s1s2…) y t = (t0t1t2…) dos puntos arbitrarios en ∑. Una función distancia en ∑, dada por
.
Esta función d, es llamada una métrica en ∑, si para cualesquiera s,t,u ∈ ∑, cumplen las siguientes tres propiedades:
- d[s,t] ≥ 0, y d[s,t] = 0, si y solo si t = s.
- d[s,t] = d[t,s].
- d[s,t] ≤ d[s,u]+d[u,t].
En efecto,
1. d[s,t] ≥ 0, siempre se tiene, por como esta definida la función d.
d[s,t] = 0, si y solo si s = t. Si d[s,t] = 0, entonces por definición de d, d[s,t] = , lo que implica |si - ti| = 0, para cada i, con i = 1,2,…, lo que significa s = t, por igualdad de elementos. Análogamente, si s = t, entonces d[s,t] = 0.
2.
3. , luego, por ser ℝ, con el valor absoluto un espacio métrico, se tiene
Por consiguiente, d[s,t] ≤ d[s,u] + d[u,t].
El par (∑, d) es llamado un espacio métrico.
El Conjunto de Cantor
Aquí, definiremos el conjunto de Cantor de dos maneras diferentes: una que es bastante intuitiva y que se podría clasificar de tipo geométrico, y otra de manera más formal en el sentido de la dinámica simbólica. En otras palabras, caracterizaremos a los elementos de este conjunto, como aquellos puntos de intervalo [0,1] ⊂ ℝ, cuya expansión ternaria sólo aparecen las cifras 0 y 2, lo cual simplificará el trabajo para resultados posteriores.
Construcción del Conjunto Ternario de Cantor
Consideremos el intervalo I = [0,1] ⊂ ℝ y el sistema dinámico asociado a una función de tipo tienda campaña, esta función es
.
En el espacio de fase de los números reales, es decir, el sistema dinámico ( ℝ, f). Cuya representación gráfica se presenta en la Figura 1.
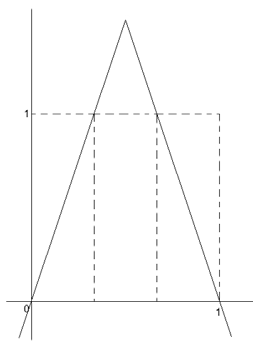
Figura 1.
El objetivo que aquí nos planteamos, es el de determinar cuál es conjunto de C ⊂ ℝ, de todos los puntos cuya órbita no diverge a infinito, es decir
pues si alguna órbita diverge a infinito ha de ser, obviamente a, -∞, puesto que
f(x) ≤ f(1 ⁄ 2) = 3 ⁄ 2,
para todo x ∈ ℝ.
Para determinar este conjunto, vemos gráficamente, el análisis de las órbitas de todos los puntos que están fuera del intervalo [0,1], que divergen a menos infinito, ver Figura 2.
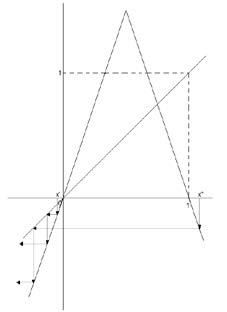
Figura 2.
Luego, el conjunto de puntos cuya órbita no diverge a menos infinito, ha de estar contenido en el intervalo [0,1], es decir
C ⊂ [0,1].
Ahora, si consideramos un punto x ∈ [0,1], cuya órbita se sale del cuadrado unidad, [0,1] × [0,1], en algún instante de su recorrido, esto es fk (x) > 1, para algún k ≥ 1. Entonces su órbita diverge a menos infinito, considerando el análisis gráfico hecho anteriormente, se tiene (ver Figura 3).
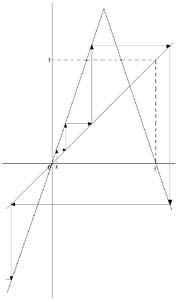
Figura 3.
Además, si la órbita de x, no sale del cuadrado unidad en ningún instante de su recorrido, es claro que su órbita está acotada y por tanto x ∈ C.
Por consiguiente, el conjunto C de los puntos x ∈ ℝ, cuya órbita permanece acotada, es el conjunto de los puntos del intervalo [0,1], cuya órbita no se sale nunca del cuadrado unidad. Además, es evidente que si x ∈ [0,1], su órbita se sale del cuadrado unidad cuando, para algún k > 1, fk (x) > 1.
Ahora, si llamamos A1 el conjunto de puntos x ∈ [0,1], cuya órbita se sale del cuadrado unidad en el primer paso, esto es,
A1={x ∈ [0,1] : f(x)>1}.
Análogamente, si A2 es el conjunto de puntos x ∈ [0,1], cuya órbita se sale del cuadrado unidad, por primera vez, en el segundo paso
A2={x ∈ [0,1] : 0 ≤ f (x) ≤ 1, y f2 (x) > 1},
y así reiteradamente, se obtiene de manera general para An, el conjunto de los puntos x ∈ [0,1] cuya órbita se sale del cuadrado unidad, por primera vez, en el paso n-ésimo
An={x ∈ [0,1] : 0 ≤ f (x), f2 (x),…,f(n-1) (x) ≤ 1 ; fn (x) > 1}.
Entonces, se tiene que
,
Siendo los conjuntos , disjuntos dos a dos
Ahora, determinemos cada uno de estos conjuntos; observando la Figura 4, se puede ver que A1, está formado por el intervalo abierto cuyos extremos son las abscisas de los puntos de cortes de f con la recta y = 1, y dichos cortes, son las raíces de las ecuaciones
3x = 1 y 3 (1 - x) = 1
que son x = 1/3 y x = 2/3. Luego,
por lo cual
,
donde son dos intervalos cerrados de longitud 3-1, cada uno de ellos, de esta forma
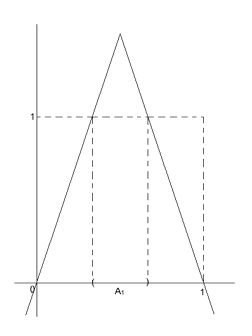
Figura 4.
Para determinar A2 ⊂ [0,1] - A1, convine observar que, f aplica en I, e en I, luego, habrá dos intervalos abiertos, uno dentro de y otro dentro de , a los que f2 aplicará fuera del cuadrado unidad. Estos intervalos estarán formados por aquellos puntos de x ∈ [0,1]\A1 tales que f(x)∈A1
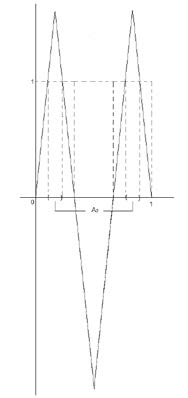
Figura 5.
Luego, por geometría elemental, se puede ver que A2 está formado por los intervalos abiertos centrados dentro de e , y de longitud 1 ⁄ 3, de las longitudes de , i = 1,2. Esto es,
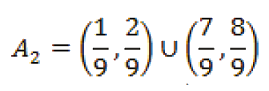
Así, C estará contenido en los 22 intervalos cerrados, de longitud 3-2 cada uno de ellos, esto son, los que quedan al extraer de [0,1] - A1 el conjunto A2, ver Figura 5. Es decir,
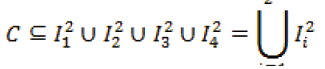
donde
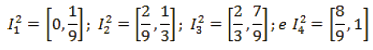
Para determinar A3, basta con repetir el razonamiento anterior y observar que f aplica cada subintervalo , i = 1,2,3,4, en todo el intervalo [0,1]. Luego, f3 aplicará fuera del cuadrado unidad a aquellos puntos x ∈ tales que f2 (x) ∈ A1 y que son, por geometría elemental, los puntos del intervalo abierto centrado en , de longitud 1⁄3 de su longitud, es decir, de longitud 3-3, ver Figura 6.
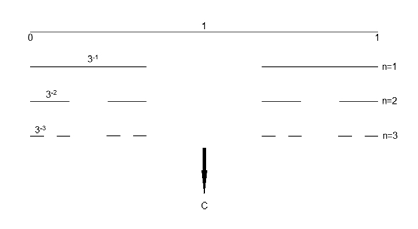
Figura 6.
Por lo tanto, A3 estará formado por 22 intervalos abiertos de longitud 3-3, y centrados en cada uno de los intervalos , i = 1,2,3,4. Luego, C estará contenido en los 23 intervalos cerrados, de longitud 3-3 cada uno de ellos; siendo los que quedan al quitar de [0,1] - (A1 ∪ A2) el conjunto A3, ver Figura 6. Es decir
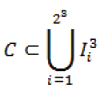 ,
,
donde
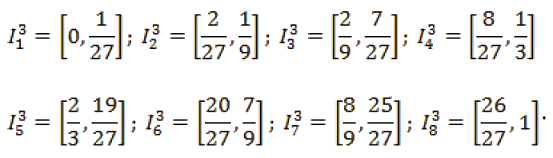
Y así sucesivamente. En el límite de este proceso infinito nos quedará el conjunto C, que estamos buscando; cuya órbita de los puntos de éste conjunto permanecen acotado, y que se es conocido como el conjunto clásico de Cantor. Este conjunto, se puede expresar en términos de los intervalos cerrados, que van quedando en cada paso, como
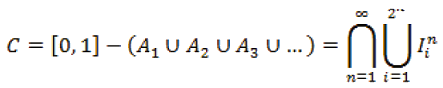
por consiguiente, se puede concluir que es un conjunto cerrado. Además, si para cada n ≥ 1, C está contenido en 2n intervalos cerrados, de longitud 3-n cada uno de ellos, entonces la longitud de C, será menor o igual que
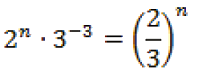 ,
,
Para cualquier n > 1, y puesto que 2/3 < 1, se cumplirá que
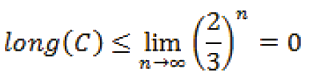 ,
,
es decir, que C es un conjunto de longitud cero.
Ahora, como bien se sabe, todo número real se puede expresar en diferentes bases; en particular si x ∈ [0,1] ⊂ ℝ, entonces podemos expresarlos en base 3, de la forma
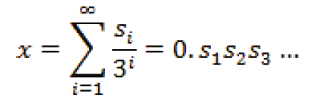 ,
,
donde si ∈ {0,1,2}. Esta expresión es llamada la expansión ternaria de x y nos servirá para dar una caracterización de los elementos de C.
Caracterización de los Elementos del conjunto de Cantor
Para hablar de la caracterización de estos elementos, es necesario recordar un poco sobre la serie geométrica:
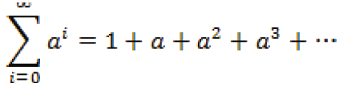
Converge absolutamente si |a|<1, esto es,
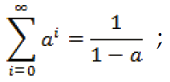
más generalmente,
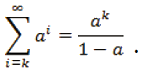
Por ejemplo, consideramos ,
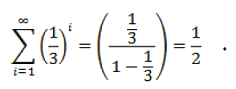
Ahora, supongamos que para cada entero positivo i, si es 0, 1, o 2. Entonces la serie
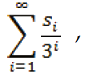
es dominada por la serie convergente
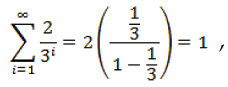
en el sentido que
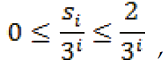
para cada i. Por lo anterior, esta serie converge y se tiene,
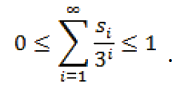
Definición. La sucesión de enteros 0.s1s2 s3…, donde cada si ∈ {0,1,2}, es llamado la expansión ternaria de x, si
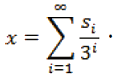
Ahora, veamos que ciertos valores de x en [0,1], puede tener dos expansiones ternarias diferentes. Por ejemplo, 1/3 tiene expansión 0.1000… y 0.0222…, pues
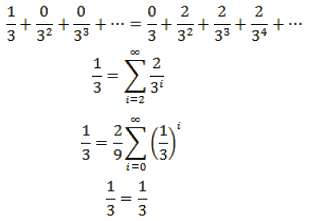
De esta manera, es fácil comprobar que la sucesión de la forma 0.s1 ...sn10 y 0.s1 ...sn02, representan el mismo número. Del mismo modo, las dos sucesiones de la forma 0.s1 ...sn20 y 0.s1 ...sn12, corresponden al mismo número. Notemos que, los números para los cuales ocurre esta ambigüedad, son precisamente los números que tienen una expansión ternaria finita, es decir, 0.s1 ...sk0, para algún k; estos son precisamente, los números racionales que pueden ser escritos de la forma p/3k , para algún entero p, con 0 ≤ p ≤ 3k.
Observemos, que si x tiene una expansión ternaria 0.s1s2…, entonces la cifra s1, determina en qué tercera parte del intervalo [0,1], x se encuentra. Si s1 = 0, entonces ; si s1 = 1, entonces ; y si s1 = 2, entonces . La razón de esto, es que la cola de la serie representa x, es decir,
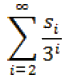
no es más grande que
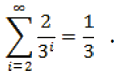
Tengamos en cuenta que los valores ambiguos de x, son exactamente aquellos que comparten dos representaciones ternarias. Así que, dada la cifra s1, sabemos en que tercera parte del intervalo unidad, x se encuentra: la parte izquierda s1 = 0, la parte media (A1 ), si s1 = 1, y la parte derecha , si s1 = 2.
Argumentando exactamente del mismo modo, vemos que el segundo dígito s2, nos dice en que tercera parte de estos subintervalos, x se encuentra. Es decir, s2 determina la tercera parte izquierda, media o derecha de los intervalos determinados en el previo párrafo. La razón de lo anterior, es que la serie
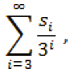
que representa la cola de la expansión ternaria, es en este caso, no más grande que 1/9. Continuando de esta manera, vemos que la expansión ternaria tiene una relación directa con los puntos del conjunto de Cantor. En particular, si x tiene una expansión ternaria y de entrada para algún s1 = 1, entonces x se encuentra en unas de las terceras partes medias de los intervalos que serán removidos durante la construcción de C. La única excepción a esto es, si x es un punto final de uno de los intervalos que forman a C, entonces, x tiene una expansión ternaria alternativa, que no tiene 1 alguno.
Conclusión
En la construcción del conjunto ternario de cantor, se hizo evidente, como se esta relacionada las diferentes áreas de las matemáticas, para la solución de un problema. Pues, este conjunto, como se mostró, no solo se puede construir de forma geométrica, sino también, por medio de la dinámica simbólica, es decir, por medio de sucesiones de cifras de 0 y 2; que nos facilitó, para la obtención de resultados como, que este conjunto es un espacio métrico, entre otros.
Referencias Bibliográficas
Martín, M.A., Morán, M. Reyes, M. (1995). Iniciación al caos. Madrid: Editorial Síntesis.
Robert L. Devaney. 1992. A first course in chaotic dynamical systems. NY: Perseus Books Publishing, L.L.C. USA.
Morris W. Hirsch, Stephen Smale y Robert L. Devaney. (2004). Diferential Equations. Dynamical Systems, and an Introduction to Chaos. San Diego California: Academic Press is an imprint of Elsevier. USA.
Robinson, C. (2000). Dynamical Systems. Boca Raton: CRC Press. USA.
Elon L. Lima. (1982). Curso de Análise. Projeto Euclides Brasil.
Simmons, G.F. (1963). Introduction to Topology and Modern Analysis. NY: McGraw-Hill Inc. International Student Edition. USA.