Artículo
Recibido el 31 de octubre de 2017/Aceptado el 30 de noviembre de 2017
ENTORNOS, Vol. 30, No. 2, Noviembre 2017
Modelo matemático que explica mejor la afectación e identifica el patrón relevante en la difusión para el dengue en la zona urbana del municipio de Neiva
Yineth Medina Arce
yineth.medina@usco.edu.co [Link]
Jeferson Antonio Ramos Tapias
jartd94@gmail.com [Link]
Resumen
El grupo de investigación BioEsMath de la universidad Surcolombiana, teniendo en cuenta la situación actual del dengue en el departamento del Huila y la manera como se expande por las comunas del municipio de Neiva, adapto el modelo matemático H SIR de (Sebastián, 2010) para explicar la afectación e identificar el patrón relevante de difusión del dengue en la zona urbana del municipio de Neiva. Esta herramienta puede ser tenida en cuenta por el SIVIGIHUILA (Ospina), para apoyar en forma científica la toma de decisiones en los programas de vigilancia y control contra la epidemia del dengue que afecta la capital huilense.
Las componentes que rigen esta investigación, es el uso de técnicas computacionales (simulación) y métodos de la matemática clásica, método numérico de Runge-Kutta de cuarto orden. El modelo costa de tres ecuaciones diferenciales ordinarias, que, aplicado a los datos reales de los infectados, 4 años y 23 semanas, se simulo la epidemia del dengue en el periodo comprendido 2013 hasta el mes de mayo del 2017, el cual afecta la salud de los pobladores y por tanto la economía y bienestar de éste municipio.
Palabras clave: Dengue; epidemiologia; Simulación; dinámica poblacional; modelos matemáticos.
Mathematical model that better explains the affectation and identifies the relevant pattern in the diffusion for dengue in the urban area of the municipality of Neiva
Abstract
The research group BioEsMath of the Surcolombiana University, taking into account the current situation of dengue in the department of Huila and the way it is expanded by the communes of the municipality of Neiva, adapted the mathematical model H SIR of (Sebastián, 2010) for explaining the affectation and identify the relevant pattern of diffusion of dengue in the urban area of the municipality of Neiva. This tool can be taken into account by the SIVIGIHUILA (Ospina), to scientifically support decision-making in surveillance and control programs against the dengue epidemic affecting the capital of Huila.
The components that govern this research, is the use of computational techniques (simulation) and methods of classical mathematics, numerical method of Runge-Kutta fourth order. The coastal model of three ordinary differential equations, which, applied to the actual data of the infected, 4 years and 23 weeks, simulated the dengue epidemic in the period from 2013 to May 2017, which affects the health of the inhabitants and therefore the economy and welfare of this municipality.
Key words: Dengue; epidemiology; Simulation; population dynamics; mathematical models.
Introducción
El dengue es hoy la más importante arbovirosis, por su gran carga de enfermedad e implicaciones sociales. Se distinguen tres formas específicas de este virus: Dengue Clásico (DC), Dengue Hemorrágico (DH), y Síndrome de choque por dengue (SCD). El mosquito Aedes aegypti, su principal transmisor con vive con el hombre en su habitad doméstico y peridoméstico, las zonas tropicales y subtropicales por debajo de los 2200 metros sobre el nivel del mar.
La revista Biomédica del Instituto Nacional de Salud (INS) de Colombia, en su edición 16, publico dos estudios de los costos del dengue para Colombia. El primero de ellos estimo que para el 2011, el promedio del costo directo era 76,1 dólares de casos ambulatorios, 70,5 dólares en pacientes hospitalizados con dengue, y de 1.115,9 en pacientes graves. El segundo estudio estimo que para el año 2012, el costo promedio de los costos directos e indirectos ascendían a 202,3 dólares, para la atención ambulatoria por dengue, para pacientes hospitalizados o caso de dengue grave los costos fueron 497, 9 y 2306,7 dólares respectivamente.
En tanto, el estudio sobre el impacto en salud pública del costo del dengue en Colombia, realizado por Raúl Castro R., docente de la facultad de Economía de la Universidad de los Andes (Bogotá- Colombia), estimo que para los años 2010 a 2012, el dengue le costó al país, 1.086,269 millones de dólares.
En el departamento del Huila, según notificación del SIVIGIHUILA (Ospina), la incidencia del dengue hasta el periodo 13 de 2013 estaba en 577,56 casos por 100.000 habitantes, superando la incidencia nacional de 426,3 por 100.000 habitantes de zona urbana; siendo el municipio de Neiva el que más casos aportaba.
El impacto económico del dengue es enorme, porque genera un incremento en los costos a todo nivel, siendo urgente el desarrollo e implementación de programas y estrategias para el control de vectores, para mejorar el conocimiento de cómo prestar servicios relacionados con el dengue, mediante enfoques integrales, que incluyan el enfoque ecológico, biológico y social. Igualmente se requiere los aportes de las Ciencias Sociales, para ayuden a entender por las personas a pesar de conocer los beneficios y peligros que supone un comportamiento dado, actúan de una manera, como si a ellos, no los fuera afectar el problema. En fin, se hace necesario actividades que apoyen: la innovación en la investigación y el desarrollo de medicamentos de investigación, conocida como la innovación empresarial social e iniciativas sociales contra el dengue, la prestación de servicios de salud y el control comunitario de vectores y tecnologías como las cortinas tratadas con insecticidas.
En la actualidad, las matemáticas están siendo utilizadas en un amplio repertorio de campos del conocimiento. De esta manera, el uso de las matemáticas aplicadas está consiguiendo combinar distintas disciplinas científicas. Uno de dichos campos en los que la matemática juega un papel fundamental es la epidemiología, la disciplina encargada del estudio de las enfermedades que afectan a humanos o animales.
Se han realizados modelos matemáticos determinísticos y estocásticos para representar la dinámica de la transmisión del dengue; los primeros son relativamente sencillos, resultan de representar un fenómeno biológico a través de la presentación y resolución de ecuaciones diferenciales ordinarias. Los modelos estocásticos involucran el término aleatorio de diversas formas, (Digiano Francis A., 1996), (Leah-Keshet, 1988).
Los modelos matemáticos aplicados a la epidemiologia tienen como objetivo proporcionar información útil en la toma de decisiones para establecer estrategias operativas en el control y/o erradicación de una enfermedad infecciosa.
Ronald Ross se conoce como el padre de los modelos epidemiológicos ya que, en 1912, con el objetivo de modelar la transmisión de la malaria realizo el primer acercamiento entre los modelos matemáticos y los fenómenos epidemiológicos. Gracias a los estudios realizados señal o acertadamente al mosquito Anopheles como el agente mediador de la transmisión de la malaria, ocho años antes de su descubrimiento. A pesar de los importantes resultados obtenidos, el modelo propuesto por Ross no se tomó en cuenta sino hasta que George McDonald retomo su trabajo, y en 1956 propuso una extensión al modelo construido que se conoce en la literatura como el modelo de Ross-McDonald (Rodrıguez, 2004).
El modelo Ross-McDonald describe el proceso de infección de la malaria a través de las interacciones entre mosquitos y humanos. Para ello utiliza un modelo compartimental que divide el estado de salud de las poblaciones de personas y mosquitos en susceptibles he infectados, empleando un sistema de ecuaciones diferenciales ordinarias.
Los modelos matemáticos basados en el modelo general de Kermack y McKendrick, 1927, que se utilizan para describir el comportamiento dinámico de la propagación de enfermedades biológicas, se definen como sistemas dinámicos, pues al ser razones de cambio con respecto al tiempo de tres niveles de estado posibles: el estado Susceptible (S), el estado Infeccioso (I) y el estado Recuperado (R), pueden ser representados con ecuaciones diferenciales (Carlos Castillo- Chaves, 2015).
El grupo de investigación BioEsMath con líneas de investigación la modelación matemática y la dinámica poblacional, conocedor de los modelos epidemiológicos compartimentales, del papel importante desempeñado de estos en el desarrollo de una mejor comprensión del mecanismo de transmisión de la epidemia y de las diversas estrategias preventivas utilizadas contra ella; además, preocupado por la manera como la enfermedad del dengue se ha expandido por el municipio de Neiva, afectando la salud de sus pobladores, y la economía general de la región, adapto el modelo matemático de H SIR de Sebastián Diego Perea (2010). Esta herramienta matemática, permite evaluar la eficacia de las estrategias desarrolladas por salud pública del departamento del Huila y el municipio de Neiva, para la prevención y control de brotes epidémicos del dengue. Y es el resultado de un proyecto, de desarrollo e innovación, de menor cuantía, en la modalidad de financiación dirigida a los grupos de investigación de la universidad Surcolombiana.
El modelo matemático adaptado HSIR, consiste en un sistema de tres ecuaciones diferenciales ordinarias, representa los estados de salud de los pobladores de Neiva: susceptible (S), infeccioso (I) y recuperado(R); describe los cambios en el número de los individuos de cada uno de los estados, permite realizar el análisis cualitativo que contiene el análisis local del único equilibrio endémico positivo y se puede establecer las condiciones suficientes para la estabilidad global este equilibrio positivo único. También, se estimó los parámetros del modelo, con los cuales se realizaron las simulaciones; finalmente el modelo fue contrastado con el caso real del municipio de Neiva, se tomaron los datos suministrados por los boletines departamentales epidemiológicos, para el periodo comprendidos desde el 2013 hasta las primeras 23 semanas del 2017.
Metodología
Antecedentes
Una enfermedad transmitida por un vector es aquella en que un organismo patógeno, responsable de la enfermedad, no se puede transmitir directamente entre humanos. El responsable de la transmisión de la enfermedad se denomina vector. Los vectores pueden ser mamíferos, pájaros, artrópodos e insectos. Las enfermedades para las cuales un mosquito es el encargado de la transmisión de la enfermedad, como el dengue, la fiebre amarilla, el Chikunguña y la malaria; constituyen uno de los problemas más grandes y de mayor impacto en la salud pública a nivel mundial. Se calcula que sólo la infección del Dengue cobra 25 mil vidas al año, según la Organización Mundial de la Salud (OMS) y afecta negativamente a las economías nacionales de la región.
El virus del dengue es un flavivirus del género Togaviridae, que ocurre con cuatro serotipos distintos, estos son biológicamente transmitidos de un humano infectado a un susceptible, a través de la picadura del mosquito hembra vector Aedes aegypti (artrópodo); este virus se propaga en zonas tropicales y subtropicales por debajo de los 2.200 metros sobre el nivel del mar. Se distinguen tres formas específicas: Dengue Clásico (DC), Dengue Hemorrágico (DH) y Síndrome de Choque por Dengue (SCD), cada una con diversos tipos de gravedad (Juan, 2004), (F.G., 2002).
La Carga mundial de dengue. Según informe de la organización mundial de salud, en las últimas décadas ha aumentado enormemente la incidencia de dengue en el mundo. El número real de casos de dengue está insuficientemente notificado y muchos casos están mal clasificados. Según una estimación reciente, se producen 390 millones de infecciones por dengue cada año (intervalo creíble del 95%: 284 a 528 millones), de los cuales 96 millones (67 a 136 millones) se manifiestan clínicamente (cualquiera que sea la gravedad de la enfermedad).1 En otro estudio sobre la prevalencia del dengue se estima que 3900 millones de personas, de 128 países, están en riesgo de infección por los virus del dengue (Brady Oj, 2012).
Los Estados Miembros de tres regiones de la OMS notifican sistemáticamente el número anual de casos. El número de casos notificados pasó de 2,2 millones en 2010 a 3,2 millones en 2015. Aunque la carga total de la enfermedad a nivel mundial es incierta, el comienzo de las actividades para registrar todos los casos de dengue explica en parte el pronunciado aumento del número de casos notificados en los últimos años. Otra característica de la enfermedad son sus modalidades epidemiológicas, en particular la hiperendemicidad de los múltiples serotipos del virus del dengue en muchos países y la alarmante repercusión en la salud humana y en las economías nacional y mundial.
El dengue grave (conocido anteriormente como dengue hemorrágico) fue identificado por vez primera en los años cincuenta del siglo pasado durante una epidemia de la enfermedad en Filipinas y Tailandia. Hoy en día, afecta a la mayor parte de los países de Asia y América Latina y se ha convertido en una de las causas principales de hospitalización y muerte en los niños y adultos de dichas regiones.
Hasta la semana epidemiológica 11 de 2017, la Región de las Américas había notificado 50 172 casos, cifra inferior a la registrada en el mismo periodo en años anteriores. En la Región del Pacífico Occidental se han notificado brotes de dengue en varios Estados Miembros, y la circulación de los serotipos DENV-1 y DENV-2 (Salud, 2017)
En el año 2013 en Colombia al término del periodo 13 se han notificado en el Sistema de Vigilancia Salud Pública (SIVIGILA) del Instituto Nacional de Salud: 110.036 casos totales de dengue, 107.289 (97.5%) de dengue y 2.747 (2,5%) dengue grave. La incidencia acumulada nacional de dengue año 2013 es de 426.3 * 100000 habitantes; cuya población a riesgo corresponde a la población urbana de país, (Ospina).
La incidencia de dengue hasta el periodo 13 de 2013 está en 577,6 casos por 100.000 habitantes en el departamento del Huila y superando la incidencia nacional de 426,3 por 100.000 habitantes de zona urbana. Los siete municipios que aportan actualmente más casos en orden de mayor a menor son Neiva, Garzón, Pitalito, Palermo, Tesalia, La Plata, Aipe, Rivera, Campoalegre, Algeciras, Timaná y Paicol, como lo nombra Sistema de Vigilancia de la salud del Huila (SIVIGILAHUILA), (Ospina).
En tanto, Cerquera, Rodríguez, Navarrete (2013), publicaron en la revista de la facultad de salud, vol. 5, de la universidad Surcolombiana, artículo sobre la situación actual del dengue en el departamento del Huila; quienes realizaron un diagnóstico de salud para dengue en el departamento del Huila en el contexto colombiano. Así mismo, realizaron una caracterización epidemiológica del dengue como variable en su comportamiento y compararon algunas de sus características clínicas con el contexto nacional. Encontraron una tasa de ataque de 44x100.000 habitantes para el departamento del Huila ubicándolo en el octavo puesto de los 31 departamentos de Colombia.
Entre la tercera y sexta semana, encontraron un comportamiento de alerta epidémica. La incidencia fue mayor en la población urbana y entre los jóvenes.
Algunas variables de interés de los casos de dengue muestran que afecta más al género masculino con 53% de los casos, femenino 47%. El 83% de los casos reportados de dengue proceden del área urbana, 6% de centros poblados y 11% del área rural dispersa. El 55% pertenecen al régimen subsidiado, 32% al régimen contributivo y los demás regímenes excepción, especial y los no afiliados, cada uno con el 4% respectivamente, ya que se puede ver en (Luis Villar, 2015). La distribución de los casos de dengue y dengue grave continúa con predominio en edades tempranas, niños y adolescentes con un 64% de los casos en menores de 19 años. En cuanto al género, la enfermedad ha afectado en un 53% a hombres y en 47% a mujeres, sin diferencias significativas. El 54% de los casos de dengue grave se han presentado en el rango de edad de 0 a 9 años con leve diferencia por sexo, y el 29% en menores de 4 años: 1 de cada 3 afectados por dengue grave es menor de 5 años, (F.G., 2002).
En la actualidad existen varias vacunas candidatas que se encuentran en desarrollo para combatir o disminuir el déficit del virus del dengue. Como parte del desarrollo clínico de una recombinante, atenuada, y tetravalente vacuna contra el dengue (CYD-TDV), se realizaron dos ensayos clínicos fase 3 en Asia y América Latina para evaluar la eficacia de transmisión de tres dosis (administrada en 0, 6, y 12 meses) contra el dengue sintomático, virológicamente confirmado (VCD). El ensayo asiático que incluyo a niños entre las edades de 2 y 14 años mostró una total eficacia de la vacuna de 56,5\% después de tres inyecciones, y esta aumentó a 80,8 % de eficacia contra el dengue grave, según lo definido por el comité de monitoreo de datos independientes, que los muestra (Juan, 2004), (Barrios, 2011) y (Luis Villar, 2015).
En la actualidad existen varias vacunas candidatas que se encuentran en desarrollo para combatir o disminuir el déficit del virus del dengue. Como parte del desarrollo clínico de una recombinante, atenuada, y tetravalente vacuna contra el dengue (CYD-TDV), se realizaron dos ensayos clínicos fase 3 en Asia y América Latina para evaluar la eficacia de transmisión de tres dosis (administrada en 0, 6, y 12 meses) contra el dengue sintomático, virológicamente confirmado (VCD). El ensayo asiático que incluyo a niños entre las edades de 2 y 14 años mostró una total eficacia de la vacuna de 56,5\% después de tres inyecciones, y esta aumentó a 80,8 % de eficacia contra el dengue grave, según lo definido por el comité de monitoreo de datos independientes, que los muestra (Juan, 2004), (Barrios, 2011) y (Luis Villar, 2015).
En este estudio, se encontró que la vacuna CYD-TDV tuvo una eficacia del 60,8 % frente VCD sintomático después de un programa de vacunación de tres dosis entre los niños entre las edades de 9 y 16 años, (Luis Villar, 2015).
Estructura del modelo H(SIR)
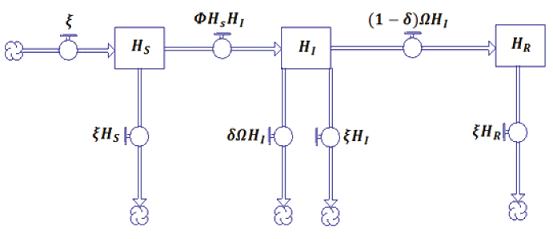
Figura 1. Diagrama de Forrester del modelo H(SIR)
Para obtener el sistema del modelo H(SIR) (Sebastián, 2010), observamos el estado Hs, Hi, HR:
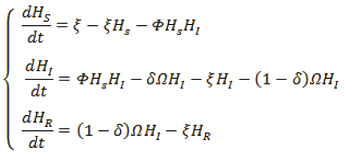
quedando,
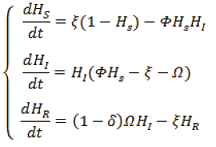 (1)
(1)
El modelo considera los tres estados frecuentes de una población cuando es infectada, estos son:
- HS, humanos susceptibles.
- HI, humanos infectados.
- HR, humanos recuperados.
Donde el grafico de HS, HI , HR se encuentran en el conjunto
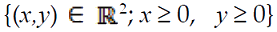
Variables de estado
- Φ: tasa de contacto para trasmitir,
- Ω: tasa del número de humanos infectados que se recuperan por unidad de tiempo,
- ξ: tasa de natalidad/mortalidad por causas naturales,
- δ: tasa del número de humanos infectados que se mueren por factor de la enfermedad.
Análisis de estabilidad del sistema
Determinar los puntos de equilibrio para el sistema.
En efecto:
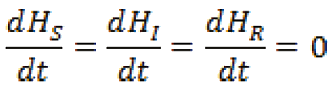
Es decir,
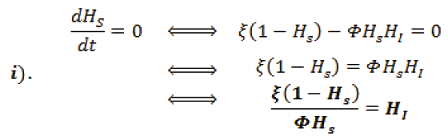
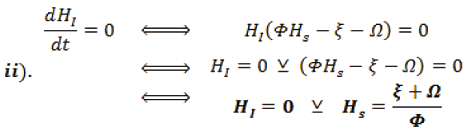
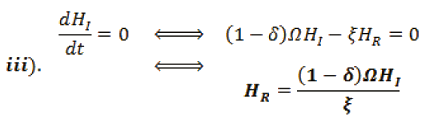
Ahora, sustituyendo ii) en i),
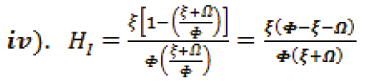
Para averiguar HR, se sustituye iv). en iii).,
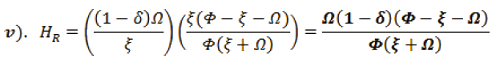
Organizando la información, se encuentra dos puntos de equilibrio para el sistema.
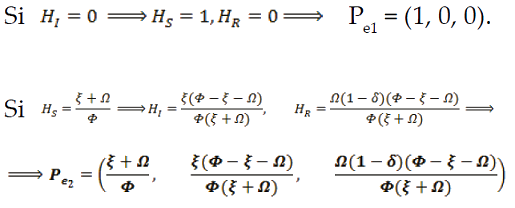
Métodos para hallar el número básico de reproducción R0.
Primer Método
Debemos saber cuando 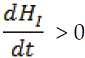 , es decir:
, es decir:
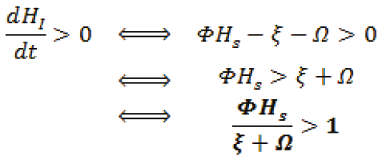
Obteniendo a R0:
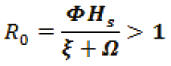
Segundo Método
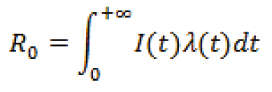
Siendo,
I(t) el número medio de nuevos infectados producidos por un individuo infeccioso en un lapso de tiempo t.
λ(t) es la probabilidad de duración de un infectado en un tiempo t1 hasta t2.
En efecto:
ΦHSHI es el flujo de entrada de los nuevos infectados. Luego I(t)=ΦHS.
El estado de los humanos infectados depende del tiempo en que estarán enfermos los individuos, para ello δΩHI, ξHI, (1-δ)ΩHI.
Esto es,
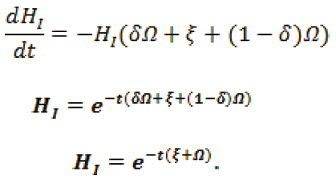
Así, 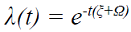 . Por consiguiente
. Por consiguiente
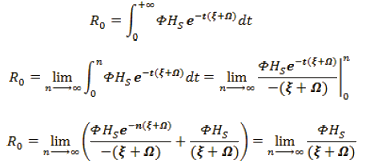
Luego
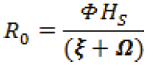
Como la población es totalmente susceptible, HS=1, quedando:
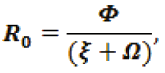
con el valor de R0, se puede analizar el Pe2. Puesto que el punto de equilibrio Pe2 está conformado por una tripleta (HS, HI, HR) donde cada valor debe ser no negativo. Esto es,
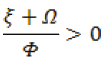 , ya que las tasas son siempre positivas,
, ya que las tasas son siempre positivas,
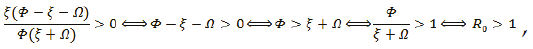
de forma análoga para,
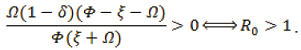
Lo cual nos quiere decir que el sistema es endémico y tiende al punto de equilibrio Pe2.
Estabilidad de los puntos de equilibrio del sistema
Siendo H=(HS, HI, HR), 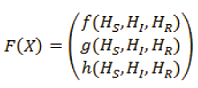
esto es,
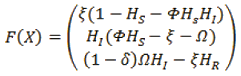
Ahora se calcula la matriz jacobiana dado X=(HS, HI, HR),
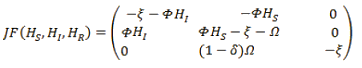
Evaluando (HS, HI, HR) = (1,0,0) en la matriz jacobiana:
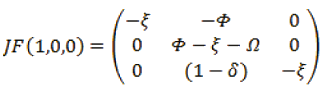
El eigenvalor de F(x) en el Pe1 = (1,0,0) es:
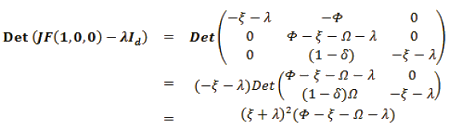
luego, los eigenvalores son:
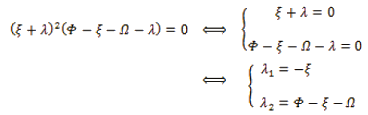
Ahora,
Si 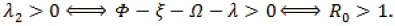
Si 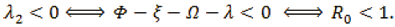
Análisis de los eigenvalores
Cuando R0 > 1. Como λ1 < 0, λ2 > 0, entonces el punto de equilibrio se llama punto silla y es inestable.
Cuando R0 < 1. Como λ1 < 0, λ2 > 0, entonces el punto de equilibrio en el origen es un nodo atractor o sumidero real. El equilibrio es estable.
Evaluando 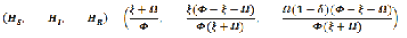 en la matriz jacobiana:
en la matriz jacobiana:
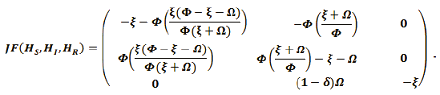
El valor propio de F(X) en el punto Pe2:
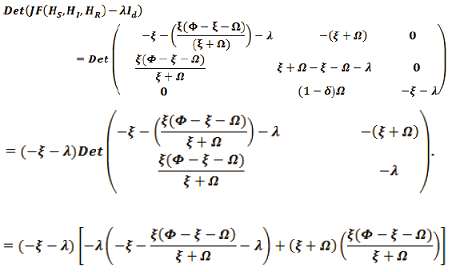
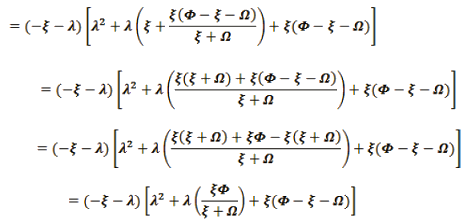
Luego, los eigenvalores son:
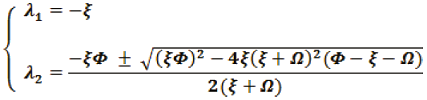
Análisis de los eigenvalores
Si la raíz es positiva y
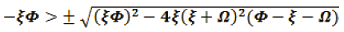 , entonces
la parte real de todos los valores propios es
negativa, por ende, es un nodo estable.
, entonces
la parte real de todos los valores propios es
negativa, por ende, es un nodo estable.
Si la raíz es compleja y la parte real es negativa entonces es un espiral estable.
Resultados
Se tomó los datos de los boletines epidemiológicos dengue en SIVIGILA de las respectivas semanas, como se muestra en la tabla 1:
Tabla 1. Número de infectados por semana durante 4 años y 23 semanas.
| SEMANA \ AÑO | 2013 | 2014 | 2015 | 2016 | 2017 |
| 1 | 21 | 88 | 70 | 72 | 40 |
| 2 | 19 | 87 | 62 | 67 | 31 |
| 3 | 24 | 110 | 40 | 67 | 24 |
| 4 | 19 | 111 | 27 | 48 | 16 |
| 5 | 24 | 146 | 28 | 35 | 16 |
| 6 | 16 | 130 | 32 | 22 | 23 |
| 7 | 31 | 131 | 22 | 27 | 14 |
| 8 | 20 | 128 | 17 | 15 | 14 |
| 9 | 18 | 127 | 21 | 12 | 9 |
| 10 | 40 | 109 | 21 | 20 | 21 |
| 11 | 24 | 113 | 18 | 16 | 6 |
| 12 | 34 | 123 | 15 | 23 | 9 |
| 13 | 30 | 107 | 13 | 23 | 20 |
| 14 | 39 | 117 | 16 | 14 | 18 |
| 15 | 39 | 116 | 16 | 12 | 10 |
| 16 | 30 | 131 | 17 | 20 | 21 |
| 17 | 37 | 115 | 26 | 18 | 20 |
| 18 | 43 | 88 | 25 | 20 | 20 |
| 19 | 38 | 89 | 44 | 15 | 17 |
| 20 | 26 | 88 | 41 | 33 | 13 |
| 21 | 32 | 77 | 26 | 13 | 14 |
| 22 | 44 | 79 | 34 | 27 | 18 |
| 23 | 34 | 57 | 20 | 32 | 13 |
| 24 | 31 | 43 | 31 | 30 | |
| 25 | 40 | 31 | 22 | 32 | |
| 26 | 38 | 30 | 58 | 38 | |
| 27 | 64 | 32 | 34 | 37 | |
| 28 | 37 | 36 | 28 | 34 | |
| 29 | 44 | 45 | 33 | 18 | |
| 30 | 51 | 34 | 31 | 33 | |
| 31 | 40 | 33 | 33 | 26 | |
| 32 | 55 | 20 | 30 | 21 | |
| 33 | 46 | 24 | 27 | 20 | |
| 34 | 63 | 26 | 34 | 19 | |
| 35 | 53 | 33 | 35 | 16 | |
| 36 | 64 | 21 | 33 | 12 | |
| 37 | 62 | 22 | 44 | 15 | |
| 38 | 58 | 23 | 28 | 19 | |
| 39 | 64 | 17 | 33 | 23 | |
| 40 | 56 | 23 | 37 | 18 | |
| 41 | 56 | 19 | 24 | 27 | |
| 42 | 56 | 15 | 43 | 41 | |
| 43 | 53 | 11 | 44 | 41 | |
| 44 | 62 | 16 | 41 | 53 | |
| 45 | 56 | 20 | 47 | 50 | |
| 46 | 62 | 26 | 55 | 51 | |
| 47 | 86 | 26 | 54 | 67 | |
| 48 | 72 | 40 | 63 | 74 | |
| 49 | 90 | 70 | 62 | 95 | |
| 50 | 120 | 112 | 70 | 58 | |
| 51 | 95 | 118 | 72 | 50 | |
| 52 | 101 | 146 | 70 | 43 |
ANÁLISIS CUALITATIVO A TRAVÉS DEL MÉTODO NUMÉRICO RUNGE-KUTTA DE ORDEN 4
Se representa mediante la siguiente grafica los valores dados en días:
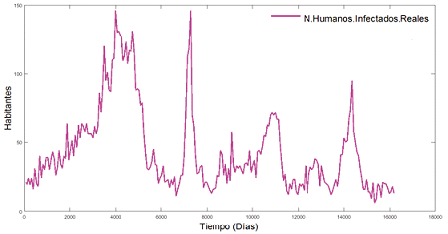
Figura 2. Número de humanos infectados reales
El modelo H(SIR) nos brinda el comportamiento geométrico de los humanos infectados del dengue al transcurso de días. Se utilizó el método numérico de RUNGE-KUTTA de orden 4.
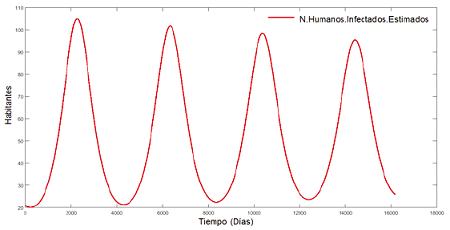
Figura 3. Número de humanos infectados estimados
Observemos el acoplamiento entre los dos gráficos:
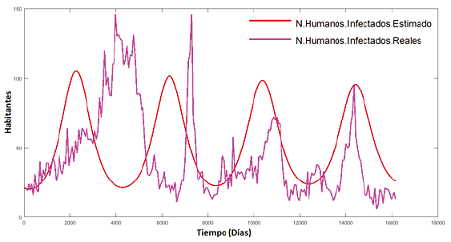
Figura 4. Humanos infectados (Reales y Estimado) estimados
Extendiendo el tiempo en 300 días se observa la siguiente ola,
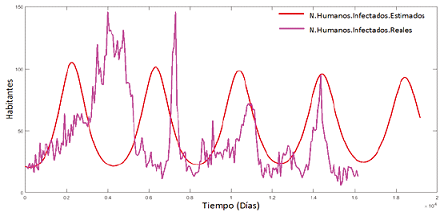
Figura 5. Humanos infectados estimados y reales en un tiempo futuro
Cada oscilación que presenta la simulación del modelo matemático, junto con los datos reales, realiza una proyección del proceso epidémico que ocurre frecuentemente en algunos lapsos de tiempo. Por ende, podemos pensar en agregar un determinado parámetro para determinar el comportamiento en épocas de fumigación o incluso que pasaría si las épocas de lluvia se extendieran.
Falta determinar el comportamiento de los humanos susceptibles y recuperados, además, de ser parte del modelo, es importante para determinar si los valores dados coinciden con el total de la población, es decir N(t) = HS + HI + HR.
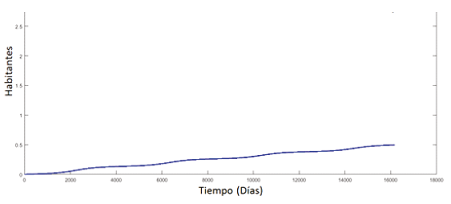
Figura 6. Humanos susceptibles y recuperados
El gráfico los humanos infectados vs susceptibles nos brindan una perspectiva de la estabilidad del sistema.
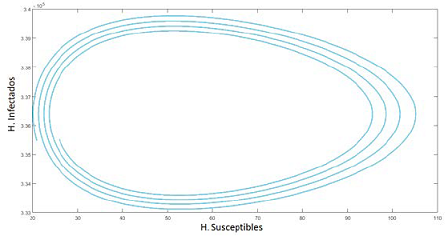
Figura 7. Plano Fase: Humanos susceptibles vs Infectados
Análisis de datos
Número básico de reproducción R0 es:
R0=2.9727.
Esto nos quiere decir que el sistema es endémico, con dos puntos de equilibrio, estos son:
Pe1 = (1,0,0) punto de equilibrio punto silla y es inestable.
Pe2 = (336363.6627, 52.008, 67039.263) punto de equilibrio nodo estable.
Valores utilizados en el modelo H(SIR):
Tabla 2. Valor de las Variables utilizadas
| Valores Iniciales | parámetros | ||
| HS | 335469 | Φ | 0.33 |
| HI | 21 | Ξ | 0.0000087 |
| HR | 0 | Δ | 0.89897 |
| T(tiempo) | 16170 | Ω | 0.111 |
El tiempo tiene una escala de 10 y los valores iniciales fueron de escala 106.
Conclusiones
La modelación matemática, es una herramienta muy útil en la representación sustancial de la dinámica de fenómenos biológicos, es bastante exacta y permite sacar conclusiones valiosas que pueden utilizarse para tomar decisiones, como medidas de control ante un brote de la enfermedad.
El modelo matemático, HSIR, en ecuaciones diferenciales describe el desarrollo y evolución de la epidemia del dengue en el municipio de Neiva desde el año 2013-2016 con 23 datos del año 2017. Datos obtenidos de los boletines epidemiológicos del dengue de la secretaria de salud departamental de la gobernación del Huila.
A pesar de las campañas de control y precaución realizada por salud pública, Neiva presenta una situación endémica de 400 días aproximadamente 57 semanas. Es decir, una ola epidémica por año con mínimo de 22 infectados y un máximo de 95 infectados por año, con tendencia a una infección de 52 individuos por año.
El R0 número reproductivo básico es de 2,9 aproximadamente, el cual es un valor bastante alto, permitiendo predecir la situación endémica de Neiva mantendrá esa periodicidad, presentando los picos más altos durante los meses de junio y julio. Efecto que se atribuye a la temperatura promedio de Neiva que es 30o acompañado con ápoca de lluvia lo que favorece la reproducción y desarrollo del mosquito Aedes Aegipty.
El modelo matemático propuesto, es suficiente para la ilustrar la aplicación de la modelación matemática en el problema de salud pública del municipio de Neiva, nos permitió estimar los parámetros del modelo, con los que se realizaron las simulaciones. Para las simulaciones se utilizó el método numérico Runge-Kutta de orden 4 en el software Matlab. Se presentaron cuatro olas, de las cuales las dos últimas olas se acercan más al comportamiento de los casos comprobados. Finalmente, un factor que puede alterar los resultados en la modelación es el cambio climático.
Referencias bibliográficas
Anderson R.M, y. M. (1992). Infectious diseases of humans: dynamics and control. Oxford University.
Barrios, J. (2011). Dynamical models described by differential inclusions in Epidemiology. The cases of HIV and dengue. Tesis doctoral, cap. 4, Universidad de la Habana-Universite desAntilles et de la Guayane.
Brady Oj, G. P. (2012). Refering the global spatial limits of dengue virus transmission by evidence-based consensus.
C., D. (1984). Models for the population dynamics of the yellow fever mosquito Aedes Aegypti. Journal of animal Ecology.
Carlos Castillo- Chaves, o. (2015). Modelos de propagación de Enfermedades Infecciosas. Cali.
Chiu. C Hoppensteadt, F. C. (1993). Analysis and computer simulation of accretion patterns in bacterial cultures.
Digiano Francis A., y. W. (1996). Process Dynamics in Environmental Systems; a wiley-interscience publication.
Elmerde, B. (2012). Estudios en Biomatemática. En B. s. Elmerde la pava salgado. Universidad Autonoma de Occidente.
Ernesto Andrade Cerquera, A. R. (2013). Situación actual de dengue en el departamento del Huila. En A. R. Ernesto Andrade Cerquera.
España, G. F. (2012). Modelamiento de la dinámica del dengue en Colombia. Bogotá.
F.G., E. (2002). Dinamica de transmisión del dengue en la ciudad de Colima. Mexico: Universidad de Colima.
Huila, G. d. (2016). Decreto de Liquidación de Presupuesto 2017. El camino es la educación.
Huila, G. d. (2016). Sistema de Gestión integrado. Informe de supervisión de contrato o convenio.
Irene, D. (2012). Dengue vector control using ether fractions from two plants (Asteraceae) as larvicide. Salud Pública.
Juan, R. R. (2004). Modelo estocastico de transmición del dengue en poblaciones estructuradas.Tesis. Universidad de Colima.
KienyKe. (25 de 9 de 2015). Salud y Bienestar. Obtenido de https://www.kienyke.com/tendencias/salud-y-bienestar/costos-deldengue-en-colombia [Link]
Leah-Keshet, E. (1988). Mathematical Models in Biology. University of Britis Columbia Vancouver, BritisColumbia, Society for industrial and applied Mathematics Philadelphia. Canadá.
Luis Villar, M. y. (8 de January de 2015). Efficacy of a Teatravalent Dengue Vaccine Children in Latin America. The New England Journal of Medicine, 372(2).
Murray, J. (s.f.). Mathematical Biology. I. An Introduction, Third Edition.
Ospina, E. C. (s.f.). Bases estadisticas de salud pública. Neiva.
Pérez, A. H. (2010). Actualización en aspectos epidemiológicos y clínicos del dengue. Revista cubana de salud pública, 36(1).
Rodrıguez, M. G. (2004). Dinamica de transmisión y modelos matemáticos en enfermedades transmitidas por vectores. Venezuela: Entomotropica.
Salud, O. M. (2016). Presupuesto por Programa 2016-2017.
Salud, O. M. (2017). Dengue y dengue grave. Obtenido de http://www.who.int/mediacentre/factsheets/fs117/es/ [Link]
Sebastián, D. d. (2010). Modelización matemática de la difusión de una epidemia de peste porcina entre granjas. Madrid.
Social, M. d. (2016). Resolución 00001288.