Otros Artículos
Recibido: 31 de agosto de 2016/Aceptado: 27 de octubre de 2016

ENTORNOS, Vol. 29, No. 2, Noviembre 2016

Aplicación de las redes neuronales artificiales y teoría de juegos al cambio climático con control óptimo

Angélica María Narváez Vivas
Universidad Surcolombiana, Colombia
anarvis93@gmail.com [Link]

Jessica Viviana Vizcaya Garzón
Universidad Surcolombiana, Colombia
jvizcayav@gmail.com [Link]

Resumen

En este trabajo se tomará como objeto de estudio el Modelo de Cambio Climático con Equilibrio Energético, el cual, revela la temperatura de la tierra y toma como puntos de partida la Línea del Ecuador y los Polos Norte y Sur. Para darle solución se tomó como base el problema de Sturn- Liouville asociado con la ecuación de difusión, el cual consiste en poner la ecuación que en su primer momento contaba con derivadas parciales y dependía de dos variables de estado (latitud x y tiempo t) para convertirla solo en términos de la variable temporal. De la misma manera se simula en el software Matlab por medio de la Red Neuronal Artificial (RNA) Fitting, la cual, se encuentra en el Toolbox de este software y que en su estructura cuenta con la combinación de las RNA's Feedforward y Backpropation, haciéndola idónea para mapear entre dos conjuntos de datos porque estas RNA's le proporcionan control óptimo.

Palabras Clave: Albedo, Redes Neuronales Artificiales RNA, Modelo Climático con Equilibrio Energético.

Application of Artificial Neural Networks and Game Theory to Climate Change with Optimal Control

Abstract

In this work it will be taken as an object of study Model Climate Change Energy Balance, which reveals the temperature of the earth and takes as starting points Line Ecuador and the North and South Poles. To give solution to this problem we took as a basis the problem of Sturm-Liouville associated with the diffusion equation, which is to put the equation that in its first moment had partial derivatives and depended on two state variables (latitude x and time t) to convert it only in terms of the time variable. In the same way is simulated in the Matlab software through Artificial Neural Network (ANN) Fitting, which is located in the Toolbox of this software and its structure has the combination of RNA's Feedforward and Backpropation, making suitable for mapping between two data sets because these RNA's give you optimal control.

Keywords: Albedo, Artificial Neural Netwokrs ANN, A Simplied One dimensional Energy Balance Climate Model.

1. Introducción

Las redes neuronales artificiales no son más que un modelo artificial y simplificado del cerebro humano, que es el ejemplo más perfecto del que disponemos para un sistema que es capaz de adquirir conocimiento a través de la experiencia. En definitiva una red neuronal es “un nuevo sistema para el tratamiento de la información, cuya unidad básica de procesamiento está inspirada en la célula fundamental del sistema nervioso humano: la neurona”. Estas, son las que actualmente están causando un mayor impacto, ya que existe una gran variedad de modelos de redes neuronales, que dependen del objetivo para la cual fueron diseñadas y del problema práctico que solucionan.

Recientemente esta tecnología ha captado la atención de muchos profesionales, tales como los dedicados a la estadística y al análisis de datos, que han incorporado las redes neuronales al conjunto de herramientas estadísticas orientadas a la clasificación de patrones y la estimación de variables continuas. Por lo tanto, el tema central en las redes neuronales artificiales en la actualidad y en el futuro radica en seguir analizando y diseñando arquitecturas de redes sistemáticas y a su vez, desarrollando sistemas de control en las RNA, conservando la optimización tradicional que consiste en un dominio administrativo con un solo objetivo de control: usuarios obedientes.

Es por esto, que se considera muy oportuno, el estudio de las RNA’s relacionado con la teoría de juegos, ya que ambas teorías radican del aprendizaje por repeticiones, además, tienen características comunes tales como el tener reglas que indican lo que debe hacer y no hacer; poseen estrategias para obtener un comportamiento o resultado final y esperado que en el lenguaje de la RNA son las funciones de activación; basan sus estrategias en datos pre-establecidos que en términos de la RNA son los datos de aprendizaje; la teoría de juegos es el estudio de problemas de decisión multipersonales que en conocimientos de la RNA son las relaciones que tienen las capas o nodos que la componen; necesitan de la optimización o el control óptimo para poder obtener lo esperado o para saber que se debe dar como resultado según los objetivos planteados, en teoría de juegos sería ganar el juego o partido y en RNA es que esta converja con un error muy mínimos.

Como es notorio el control optimo tiene un papel muy importante en cada una de ellas y es entonces donde se genera la incertidumbre si estas teorías podrían solucionar o ayudar a solucionar un Modelo de cambio climático con equilibrio energético, es decir, conseguir que un sistema que funcione de un modo más conveniente, a través del control de los sistemas reales construyendo modelos matemáticos abstractos que, por una parte expliquen el sistema y, por otra, permitan regular la evolución del mismo mediante la adopción de decisiones adecuadas (decisiones óptimas).

2. Redes Neuronales Artificiales

Red Neuronal Feedforward

Una red neuronal de FeedForward se da a conocer por el uso de técnicas de flujo de datos en un microprocesador. Como resultado de esta invención, se proporciona una red neural que tiene la capacidad de ‘aprendizaje’para distinguir entre los patrones de los datos que pueden diferir reconocible de casos idealizadas, y es capaz de realizar el reconocimiento de patrones más rápido, utilizando menos memoria y un menor número de ciclos de reloj que las redes neurales implementadas en procesadores secuenciales. Esta implementación es más simple y más rápido debido a una similitud inherente entre el flujo de información en el cerebro y en la arquitectura de flujo de datos.

El Algoritmo Backpropagation (Programación Hacia Atrás)

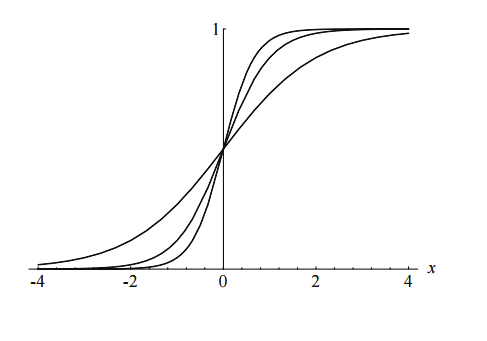
El algoritmo de backpropagation busca el mínimo de la función de error en el espacio de peso utilizando el método de descenso de gradiente. La combinación de pesos que minimiza la función de error se considera que es una soluci´on del problema de aprendizaje. Dado que este método requiere del cálculo del gradiente de la función de error, para que luego en cada paso de iteración garantizar la continuidad y diferenciabilidad de la función de error. Obviamente tenemos que utilizar una tipo de función de activación aparte de la función de paso utilizado en perceptrones, debido a que la función compuesta producida por los perceptrones es interconectadas discontinua, y por lo tanto la función de error también. Uno de los más populares funciones de activación para las redes de retropropagación es el sigmoide, un verdadero función s_c: R → (0, 1) definida por la expresión

$S_{c}(X)=\frac{1}{1\, +\, e^{-CX}}$

La constante C se puede seleccionar de forma arbitraria y su recíproco 1/c se llama el parámetro de temperatura en las redes neuronales estocásticos. La forma de los cambios sigmoideas de acuerdo con el valor de c, como se puede ver en la siguiente Figura

Figura 4.1. Tres Sigmoides, para c = 1, c = 2 y c = 3

Algoritmo

Considere una RNA con una función de red única de entrada real x y F una función. El derivado F´ (x) se calcula en dos fases:

• Feed-forward: la entrada x se introduce en la red. Las funciones primitivas en los nodos y sus derivados son evaluados en cada nodo. Los derivados se almacenan.

• Backpropagation: la constante 1 se alimenta en la unidad de salida y la red está dirigido hacia atrás. Se añade la información que llega a un nodo y el resultado se multiplica por el valor almacenado en la izquierda parte de la unidad. El resultado se transmite a la izquierda de la unidad. El resultado recogido en la unidad de entrada es la derivada de la función de red con respecto a x.

Problema Climático en las Redes Neuronales

El actual problema tiene una red feedforward de dos capas con las neuronas ocultas sigmoide y las neuronas de salida lineal (FITNET), esta RNA puede adaptarse a los problemas de asignación multidimensionales arbitrariamente, dados los datos consistentes y suficientes neuronas en su capa oculta, la red será entrenada con el algoritmo de backpropagation de Levenberg - Marquardt (trainlm), a no ser que no haya suficiente memoria, en cuyo caso se utilizará backpropagation del scaled conjugate gradient (gradiente conjugado escalado) (trainscg)

Red Neuronal Ajustada (Fitting)

En problemas de ajuste (fitting), se desea una red neuronal para mapear entre un conjunto de datos de entradas numéricas y un conjunto de objetivos numéricos. La aplicación de montaje de los nervios le ayudará a seleccionar los datos, crear y formar una red, y evaluar su rendimiento usando error cuadrático medio y el análisis de regresión

Algoritmos de entrenamiento

Levenberg marquardt

Este algoritmo requiere más memoria, pero toma menos tiempo. El entrenamiento para automáticamente cuando se detiene la generalización a mejorar, como se indica por un aumento en el error cuadrático medio de las muestras de validación.

Bayesian Regularization

Este algoritmo general requiere más tiempo, pero puede resultar bueno egeneralizando para conjuntos de datos difíciles, pequeñas o ruidosas. El entrenamiento se detiene de acuerdo con la reducción al mínimo de peso adaptativo (regularización).

Scaled conjugated gradient

Este algoritmo requiere menos memoria. El entrenamiento para automáticamente cuando se detiene la generalización a mejorar, cuando se indica un aumento en el error cuadrático medio de las muestras de validación.

3. Solución al Problema de Sturm-Liouville (SL) Asociado con la ecuación de Difusión

Consideramos la ecuación de difusión con un término de forzamiento F (x, t)

$\frac{\partial u}{\partial t}=\frac{\partial }{\partial x}\left [ p(x)\frac{\partial u}{\partial x} \right ]+q(x)u+F(x,t);\, \, \, a\leq x\leq b;\, \, \, t \leq 0$ (3.1)

con la condición de frontera

$a_{1}u(a,t)+a_{2}u_{x}(a,t)=0;\, \, \, b_{1}u(b,t)+a_{2}u_{x}(b,t)=0;\, \, \, t< 0;$

y condición inicial

$u(x,0)=f(x); \, \, \, a\leq x\leq b$

donde p(x) > 0, q(x) > 0 y f (x) son funciones de valor real y a, b, a₁, a₂, b₁, b₂ números reales

El operador L de SL

$L:\Omega \rightarrow \Omega\, '$

$u\rightarrow L(u)=\frac{\partial }{\partial x}\left [ p(x) \frac{\partial u}{\partial x}\right ]+q(x)u$

donde Ω es el conjunto de funciones continuas en [−1, 1] y Ω' es el conjunto de funciones continuas.

En terminos del operador L de SL, la ecuación (3.1) toma la forma

$u_{t}=Lu+F$ (3.2)

por el método de separación de variables para solucionar la ecuación (3.1) con F = 0 y u(x, t) = ⲫ(x)ψ(t) ≠ 0, luego la ecuación (3.1) se convierte

$\frac{\partial \psi }{\partial t}=\lambda \psi;\, \, \, t> 0;$

$L\o =\lambda \o ;\, \, \, a\leq x\leq b$ (3.3)

donde λ es una constante de separación.

las condiciones de frontera asociadas son

$a_{1}\o (a)+a_{2}\o '(a)=0;\, \, \, b_{1}\o (b)+b_{2}\o '(b)=0$ (3.4)

la ecuación (3.3) con la (3.4) es llamada Problema Sturn-Liouville asociado, el cual es resuelto facilmente encontrando los valores propios λ_n y las funciones propias ortogonales ⲫ_n(x); n = 1, 2, 3, ... De acuerdo con lo anterior, se puede escribir la solucion de (3.2) de la siguiente forma

$u(x,t)=\sum_{n=1}^{\infty }\o_{n}(x)\psi_{n}(t)$ (3.5)

donde ψ_n(t) tienen que ser determinados y se asume la función fuerza expresada en terminos de las funciones propias;

$F(x,t)=\sum_{n=1}^{\infty }f_{n}(t)\o _{n}(x)$ (3.6)

donde los Coeficientes de Fourier f_n(t) son dados así

$f_{n}(t)=< F,\o > =\int_{a}^{b}F(\xi ,t)\o _{n}(\xi )d\xi$

reemplazando (3.5) y (3.6) en (3.2) se tiene,

$\sum_{n=1}^{\infty }\o _{n}(x)\Psi _{n}(t)=L\left [ \sum_{n=1}^{\infty }\o _{n}(x)\Psi _{n}(t) \right ]+\sum_{n=1}^{\infty }f _{n}(t)\o _{n}(x) \\ =\sum_{n=1}^{\infty }\left [ \Psi _{n} L \o _{n} (x) + f _{n}(t)\o _{n}(x) \right ] \\ =\sum_{n=1}^{\infty }\left [ \lambda _{n} \Psi _{n} (t) f _{n} (t) \right ]\o _{n}(x)$

usando la ortogonalidad de las funciones propias ⲫ_n(x); n = 1, 2, 3, ...

$< \o _{n}(x),\o _{j}(x)> =\delta _{nj}$

donde δ_nj se denomina delta de Kronecker, la cual se define como

$\delta _{nj}=\left\{\begin{matrix} 0 \, si \, n \neq j\\ 1 \, si \, n = j \end{matrix}\right.$

y truncando, es decir estrayendo de la sumatoria los ⲫ_n(t) cuando n ≠ j

Da como resultado una ecuación diferencial ordinaria para ψn(t)

$\psi _{n}(t)=\lambda _{n}\psi _{n}(t)+f_{n}(t)$

Aplicando la Transformada de Laplace a esta ecuación se tiene la solución,

$\Psi _{n}=\Psi _{n}(0)e^{\lambda _{n}t}+\int_{0}^{t}e^{\left \{ \lambda _{n}(t-\tau )f _{n}(\tau) \right \}}d \tau$

para n = 1, 2, 3, ... y ψ_n(0) puede ser determinado a partir de la condición inicial

$f(x)=u(x,0)=\sum_{n=1}^{\infty }\o _{n}(x) \psi _{n}(0)$

y los Coeficientes de Fourier ψ_n(0) de la función f(x) son

$\psi _{n}(0)=< f,\o_{n}> =\int_{a}^{b}f(\xi )\o _{n}(\xi)d \xi$

4. Modelo Climático con Equilibrio Energético

En esta sección se presenta un modelo integrado y simplificado de la economía y el clima, motivado por modelos climáticos con equilibrio energético unidimensionales, el término unidimensional quiere decir que hay una dimensión espacial de una dimensión explícita en el modelo, medido en términos de las latitudes. La característica importante de estos modelos es que permiten la difusión de calor o de transporte a través de las latitudes que aumenta la relevancia de estos modelos para describir el clima.

Sea T (x; t) la temperatura de la superficie en la posición x (latitud) y t el tiempo medido en ◦C , la dinámica del clima se definen como:

$B\frac{\partial T(x,t))}{\partial }=QS(x)\alpha (x,x_{s})-\left [ A+BT(x,t)-gM(t) \right ]+D\frac{\partial }{\partial x}\left [ (1-x^{2})B\frac{\partial T(x,t)}{\partial x} \right ]$

$T_{s}=T(x_{s}(t),t)$ (4.1)

donde xs denota el seno de la latitud x, siendo −1 < x < 1, −1 denota el Polo Sur, 1 Polo Norte y 0 la línea del Ecuador. A y B son constantes usadas para relacionar el flujo de las radiaciones infrarrojas I (x, t) medidos en W/x2 con latitud x y tiempo t, con la correspondiente temperatura de la superficie T (x, t),

I (x, t) = A + BT (x, t); A = 201,4 W/x²; B = 1,45 W/x²

Q es una constante solar dividida por 4; D es un coeficiente de difusión térmica D = 0,649W/ x² ◦C; S(x, t) es la distribución meridional anual de radiación solar el cual es normalizado por la integral unidad de 0 a 1; α(x, x_s(t)) es el coeficiente de absorción del albedo en el sistema Tierraatmósfera, siendo el albedo el porcentaje de radiación que cualquier superficie refleja respecto a la radiación que incide sobre la misma y x_s(t) la latitud de la línea de hielo en el tiempo t.

En (4.2) la línea de hielo de absorción es discontinua porque el albedo (porcentaje de radiación que cualquier superficie refleja respecto a la radiación que incide sobre la misma) salta discontinuamente,

$\alpha (x, x_{s})=\left\{\begin{matrix} b_{0}=0,38 &si\, x < x_{s} &\alpha _{0}=0,697 \\ \alpha _{0}+\alpha _{2}\, .P_{2}(x) &si\, x > x_{s} & \alpha _{2}=-0,0779 \end{matrix}\right.$ (4.2)

Esta construcción de línea de hielo está determinada dinámicamente por la siguiente condición:

T > −10◦C no presente en la Línea de Hielo

T < −10◦C presente en la línea de hielo

y la función de línea de hielo x_s(t) resuelve la ecuación −10 = T (x_s(t), t).

M(t) expresa las acciones del dióxido de carbono en la atmosfera. Estas acciones afectan la evolución de la temperatura a través de la función g, y evoluciona a través del tiempo bajo el forzamiento de los insumos humanos en forma de emisiones de gases de efecto invernadero (GHGs) h(x, t) emitido en la latitud x y el tiempo t.

Para simplificar, reducimos el número de variables de estado asumiendo que M(t) esta relacionado con h(t) a través de la relación lineal simple M (t) = (1/m)h(t). Así se aproxima g(M (t)) por una relación lineal simple h(t).

En este modelo la latitud en la línea de hielo puede moverse en el tiempo en respuesta a los cambios producidos por la intervención humana, ya que la solución depende de h(t).

5. Modelo Climático con Equilibrio Energético Básico Aplicando Redes Neuronales Artificiales

Retomando el Modelo Climático del capítulo anterior y reemplazando las diferentes funciones se tiene,

$\frac{\partial T(x,t)}{\partial t}=0,65\frac{\partial }{\partial x}\left [ (1-x^{2})B\frac{\partial T(x,t)}{\partial x} \right ]-T(x,t)+\left [ \frac{t}{1,45}+(1,16-0,80x^{2})\alpha (x, x_{s})-138,9 \right ]$ (5.1)

según el Operador L del Problema SL,

p(x) = 1 − x²; q(x) = −1; a = −1; b = 1 y

$F(x,t)=\frac{t}{1,45}+(1,16-0,80x^{2})\alpha (x, x_{s})-138,9$

y según el Modelo de Cambio Climático del capítulo anterior,

$gM(t)=\frac{t}{1,45}$ y $QS(x)=1,16 - 0,80x^{2}$

la condición de frontera,

T_s = T (x_s (t), t) = -10

la condición inicial tomando t = 0 cuando son las 12 de la noche

T_s(x, 0) = −34; t = 0 = 12 p.m.

$\alpha (x, x_{s})=\left\{\begin{matrix} 0,38 &si\, x> x_{s} \\ 0,73595-0,11685x^{2} &si\, x < x_{s} \end{matrix}\right.$ (5.2)

Ya que la función del albedo hace la ecuación (5.1) discontinua, dificultando la solución de esta, se toma la función del albedo como α(x, xs) = 0,73595 − 0,11685x2, aclarando que queda para estudios posteriores la solución con la función del albedo original, luego la ecuación para todo x de (5.1),

$\frac{\partial T(x,t)}{\partial t}=0,65\frac{\partial }{\partial x}\left [ (1-x^{2})B\frac{\partial T(x, t)}{\partial x} \right ]-T(x, t)+\left [ \frac{t}{1,45}-138,46-0,30x^{2} \right ]$ (5.3)

T_s = T (x_s(t), t) = −10

T_s = −34; t = 0 = 12 p.m.

Usando el método explicado en el capítulo 3, del método de separación de variable para buscar una solución a la ecuación (5.2) con t/1,45 − 138,46 − 0,30x² = 0, con T (x, t) = a(t)e^ix ≠ 0, es decir las propias ortoganles ⲫ = e^ix, por lo tanto la ecuación (5.3) se convierte en,

$\frac{de^{ix}}{dt}=\lambda e^{ix};\,\, t > 0 \\ \\ La(t)=\lambda a(t);\,\, -1\leq x\leq 1$ (5.4)

La ecuación (5.1) puede ser resuelta de manera fácil encontrando los valores propios λ_n y tomando las funciones propias ortogonales ⲫ_n(x) = e^inx; n = 1, 2, 3, . . . De acuerdo con el principio lineal de superposición, se puede escribir la solución de (7.3) de la siguiente manera

$T(x, t)= \sum_{n=1}^{\infty }a_{n}(t)e^{inx}$ (5.5)

Donde a_n(t) deben ser encontrados.

Luego, la funcion fuerza es expresada en términos de las funciones propias,

$F(x, t)= \sum_{n=1}^{\infty }f_{n}(t)e^{inx}$

donde los Coeficientes de Fourier fn(t) son dados por;

$f_{n}(t)=\left \langle F,e^{inx} \right \rangle = \int_{-1}^{1}\left ( \frac{t}{1,45-138,46-0,30\xi ^{2}} \right )e^{in\xi }d\xi = \frac{2(500t-100456)e^{inx}}{725}d\xi$

Luego,

$F(x, t)=\sum_{n=1}^{\infty }\frac{2(500t-100456)e^{inx}}{725}$

Reemplazando (5.4) y (5.5) en (5.3) se obtiene,

$\sum_{n=1}^{\infty }a_{n}^{.}(t)e^{inx}=\sum_{n=1}^{\infty }\left [ a_{n}(t)Le^{inx}+\frac{2(500t-100456)e^{inx}}{725} \right ]=\sum_{n=1}^{\infty }\left [ \lambda _{n}a_{n}(t)+\frac{2(500t-100456)e^{inx}}{725} \right ]$ (5.6)

como resultado da la ecuacion diferencial ordinaria para a_n(t)

$\dot{a}_{n}=\lambda _{n}+\frac{2(500t-100456)}{725}$

donde n = 1, 2, 3, ...

Se obtiene los valores propios λn

$Le^{inx}=\lambda _{n}e^{inx}\leftrightarrow -n^{2}e^{inx}=\lambda _{n}e^{inx}$

además,

$\lambda _{n}=\left \langle Le^{inx},e^{in\, x} \right \rangle$

luego, λ_n = -(n² + 1)

Aplicando la transformada de Laplace a (5.6) se obtiene la solución,

$a_{n}(t)=a_{n}(0)e^{-(n^{2}+1)t}+\int_{0}^{t}e^{\left [ -(n^{2}+1)(t-\tau )f_{n}(\tau) \right ]}d\tau$

donde n = 1, 2, 3, ... y a_n(0) pueder ser determinada por la condición inicial

$f(x)=T(x, 0)=\sum_{n=1}^{\infty }a_{n}(0)e^{inx}=-34$

y los Coeficientes de Fourier a_n(0) de la función f (x) son dadas por

$a_{n}(0)=\left \langle f, e^{inx} \right \rangle=\int_{-1}^{1}-34e^{in\xi }d\xi =\frac{34i(e^{in}-e^{-in})}{n}$

ahora,

$\int_{0}^{t} e^{[- (n^{2} + 1) (t - τ) f_{n} (τ)} dτ = \frac{725}{8 (n^{2} + 1) 125 t - 25114)} [1 - e^{[\frac{8 t}{725} (n^{2} + 1) (125 t - 25114)]}]$

La solución de (5.3),

$a_{n} (t) = \frac{- 34 i (e^{in} - e^{- in}) e^{- (n^{2} + 1) t}}{n} + \frac{725}{8 (n^{2} + 1) 125 t - 25114)} [1 - e^{[\frac{8 t}{725} (n^{2} + 1) (125 t - 25114)]}]$

Ya que las cinco primeras a_n consumen toda la energía del sistema, es decir a partir del a₆, ... la energía de estas funciones es cero, no influyendo en la solución del Modelo Climático con Equilibrio Energético Básico. Se define a partie de las a_n; n = 1, 2, 3, 4, 5,

$a_{1} (t) = - 34 i (e^{i} - e^{- i}) e^{- 2 t} + \frac{725}{16 (125 t - 25114)} [1 - e^{\frac{16 t (125 t - 25114))}{725}}]$

$a_{2} (t) = \frac{- 34 i (e^{2 i} - e^{- 2 i}) e^{- 5 t}}{2} + \frac{725}{40 (125 t - 25114)} [1 - e^{\frac{40 t (125 t - 25114))}{725}}]$

$a_{3} (t) = \frac{- 34 i (e^{3 i} - e^{- 3 i}) e^{- 10 t}}{3} + \frac{725}{80 (125 t - 25114)} [1 - e^{\frac{80 t (125 t - 25114))}{725}}]$

$a_{4} (t) = \frac{- 34 i (e^{4 i} - e^{- 4 i}) e^{- 17 t}}{4} + \frac{725}{136 (125 t - 25114)} [1 - e^{\frac{136 t (125 t - 25114))}{725}}]$

$a_{5} (t) = \frac{- 34 i (e^{5 i} - e^{- 5 i}) e^{- 26 t}}{5} + \frac{725}{208 (125 t - 25114)} [1 - e^{\frac{208 t (125 t - 25114))}{725}}]$

Por ultimo, el Modelo Climático con Equilibrio Energético Básico, el cual depende únicamente de la variable temporal,

$T (x, t) \approx a_{1} (t) + a_{2} (t) + a_{3} (t) + a_{4} (t) + a_{5} (t)$

Simulación del Modelo Climático con Equilibrio Energético Básico

Para el objetivo de estudio se encontraron soluciones (plot de temperatura) a partir de un algoritmo particular (anexo 1) donde el plot muestra las siguientes cinco gráficas

Figura 5.1. a_n; n = 1, 2, 3, 4, 5

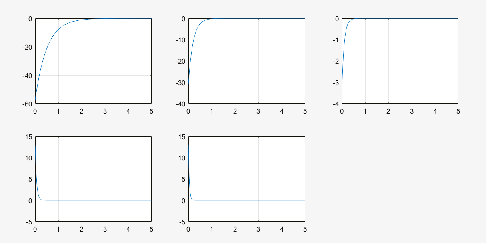
Problema climático en las redes neuronales

La Figura 5.2 es la topología de la red neuronal tratada:

Figura 5.2.

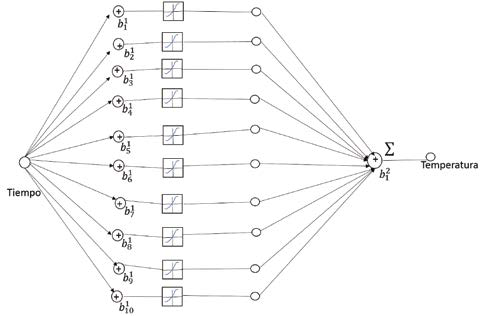
donde los b¹_i, i = 1, 2, ..., 10 son las capas ocultas de la RNA.

El actual problema tiene una red feedforward de dos capas con las neuronas ocultas sigmoide y las neuronas de salida lineal (FITNET), esta RNA puede adaptarse a los problemas de asignación multidimensionales, dados los datos consistentes y suficientes neuronas en su capa oculta.La red será entrenada con el algoritmo de backpropagation de Levenberg - Marquardt (trainlm), a no ser que no haya suficiente memoria, en cuyo caso se utilizar´a backpropaga- tion del scaled conjugate gradient (gradiente conjugado escalado) (trainscg).

Configuración de la Red Neuronal

En el software matemático MATLAB, se us´o la RNA para cada a_n; n = 1, 2, 3, 4, 5 logrando determinar la funci´on de transferencia Tansig, como la más adecuada para la primera capa por su flexibilidad, ya que permite dar resultados en valores negativos como positivos. El software utiliza esta función mejorando el entrenamiento de la red y la velocidad de convergencia.

En la segunda capa está la salida y posee una función de transferncia lineal (no se limitan las salidas), en MATLAB se llama Purelin, en donde se utilizan comunmente en problemas como el presente (de ajuste).

La Figura 5.3 ilustra la configuración adecuada de la función de transferencia para cada capa:

Figura 5.3.

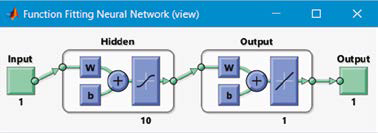
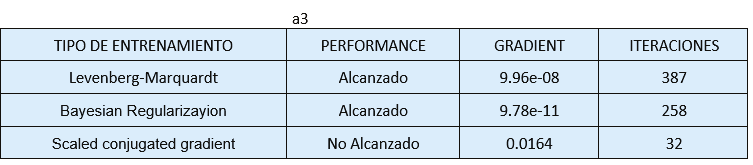
El algoritmo de entrenamiento adecuado para los a₁, a₂ y a₃ es el de Levenberg- Marquardt.

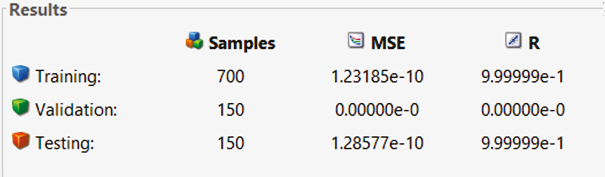
Mientras el algoritmo de entrenamiento adecuado para a₄ y a₅ es el de Bayesian Regularization.

Para la RNA se utilizó una validación simple con un procentaje del 70% del tiempo para el entrenamiento, 15% para validación y 15% para el test. El tiempo que se tomó para la aplicación fue de 5 (cinco) segundos, el cual se dividió en 1000 intervalos para su mejor aproximación en la solución. Es decir, que para el entrenamiento de la RNA escogiera 700 (setecientos) de dichos intervalos, 150 (ciento cincuenta) para su validación y 150 (ciento cincuenta) para el test.

Resultados

Matlab realiza calculos para el análisis de los resultados mostrando R para cada curva de entrenamiento (Entrenamiento, validación y prueba), las pruebas con los tipos de entrenamientos, se muestran en las siguientes tablas para cada a_n:

Tabla 5.1 a₁

Tabla 5.2 a₁

Tabla 5.3 a₂

Tabla 5.4 a₂

Tabla 5.5 a₃

Tabla 5.6 a₃

Tabla 5.7 a₄

Tabla 5.8 a₄

Tabla 5.9 a₅

Tabla 5.10 a₅

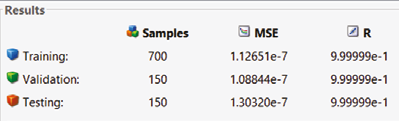
Comparando los plot del algoritmo y los plot utilizando redes neuronales artificiales, se encontro la app de Neural Net Fitting es la mas adecuada al problema presentado.

El plot realizado por la RNA de las respectivas an son los siguientes

Figuras 5.4 a₁ y a₂

Figuras 5.5 a₃ y a₄

Figuras 5.6 a₅

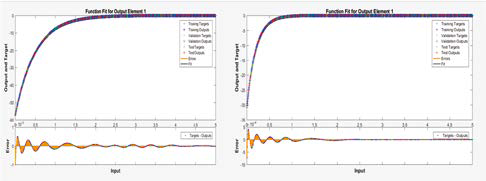
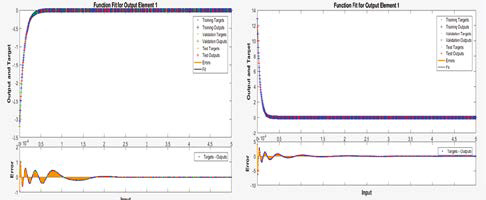
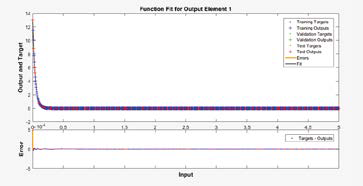
6. Conclusiones

El modelo climático con equilibrio energético, al ser modelado en términos económicos, ya posee control óptimo, sin embargo en la RNA utilizada, la cual, es la RNA backpropaggation, ya lo posee en su estructura, siendo esta idónea en el tratamiento de este modelo climático.

Al observar que el modelo climático tiene la estructura del problema de Sturn-Liouville asociado con la ecuación de Difusión, se desarrolló el método expuesto para su solucion, el cual es el método separación de variable o tambien llamado Método de Galerkin, expresando la solución como una serie de Fourier, tomando las funciones propias ortogonales como la exponencial compleja.

Como se mencionó anteriormente la ecuación del Albedo al ser discontinua, convertía (5.1) en una ecuación en derivadas parcial discontinua, por lo tanto, modificamos la ecuación del ALbedo para que (5.1) fuera continua, aclarando que esta queda para estudios posteriores.

La solución del Modelo Climático con Equilibrio Energético Básico consta de la sumatoria de las cinco primeras a_n porque estas son las que toman toda la energía del sistema.

El software matemático MATLAB ofreció las herramientas adecuadas para el problema aplicado al clima y se desempeñó de manera correcta las redes neuronales en dicha problemática.

El uso de redes neuronales como herramienta de solución de modelos climáticos permite resultados muy favorales independientemente del número de datos.

Utilizando la arquitectura planteada para la red neuronal se evaluaron los tipos de entrenamiento, de los cuales se presentó mejor resultado fueron los algoritmos Levenberg Marquardt y bayesian regularization.

Para la arquitectura de la red neuronal se utilizó la red de tipo backpropagation; cuyo números de neuronas en la primera capa corresponde al número de capas ocultas que se escogieron para la red (10), y una capa de salida que entrega un valor positivo.

7. Anexos

El siguiente es el código que genera el software Matlab, después de introducir los datos en la RNA;

Anexo 1.

t=linspace(0,5,1000); % De cero a 5 segundos k=5; % De uno a 5 gráficas (funciones)

for n=1:k

a1(n, :)=(((34i)*(exp(1i*n)-exp(-1i*n)))/n)*exp(-(n² + 1) ∗ t);

a2(n, :) = 725./(8 ∗ (n2 + 1) ∗ (125 ∗ t − 25114));

a3(n, :) = 1 − exp(((8 ∗ t)/725) ∗ (n+1). ∗ (125 ∗ t − 25114));

a(n, :) = a1(n, :) + a2(n, :). ∗ a3(n, :)

subplot(2, 3, n);

plot(t, a(n, :));

grid on;

end

Anexo 2.

%SolveanInput-OutputFittingproblemwithaNeural Network

%ScriptgeneratedbyNeuralFittingapp

%Created13 − Sep − 201613: 44: 46

%Thisscriptassumesthesevariablesaredefined:

%t − inputdata.

%a11 − targetdata.

x = t;

t = a11;

% Choose a Training Function

% For a list of all training functions type: help nntrain

% ’trainlmís usually fastest.

% ’trainbr’takes longer but may be better for challenging problems.

% ’trainscgu´ses less memory. Suitable in low memory situations.

trainFcn = ’trainlm’; % Levenberg-Marquardt backpropagation.

% Create a Fitting Network hiddenLayerSize = 10;

net = fitnet(hiddenLayerSize,trainFcn);

% Setup Division of Data for Training, Validation, Testing

net.divideParam.trainRatio = 70/100;

net.divideParam.valRatio = 15/100;

net.divideParam.testRatio = 15/100;

% Train the Network

net,tr

= train(net,x,t);

% Test the Network

y = net(x);

e = gsubtract(t,y);

performance = perform(net,t,y)

% View the Network

view(net)

% Plots

% Uncomment these lines to enable various plots.

%figure, plotperform(tr)

%figure, plottrainstate(tr)

%figure, ploterrhist(e)

%figure, plotregression(t,y)

%figure, plotfit(net,x,t)

Referencias

[1] Anastasios Xepapadeas- William Brock - Gustav Engstrom , Energy Balance Climate Models, Damage Reservoirs and the Time Profile of Climate Change Policy, The Oxford Handbook of the Macroeconomics of Global Warming, Mayo, 2015.

[2] Asu Ozdaglar, Networks Challenge: Where Game Theory Meets Network Optimization, Julio, 2008.

[3] Chai Wah Wu, Control of Networks of Coupled Dynamical, Springer, 2013.

[4] Gibbons Robert, Un primer curso de teoría de juegos, Universidad de Cornell.

[5] Kalle Parvin- Mikko Heino - Ulf Dieckman, Function-valued Adaptive Dynamics and Optimal Control Theory, Mathematical Biology, April 4 2012.

[6] Lokenath Debnath, Nonlinear Partial Differential Equations for Scientists and Engineers, Second Edition.

[7] Miguel De Guzman, “Ecuaciones Diferenciales Ordinarias, Teoría de Estabilidad Y Control”. Alhambra

[8] Nejib Smaoui- Suad Al-Enezi, Modelling the Dynamics of Nonlinear Partial Differential Equations Using Neural Networks, Journal of Computational and Applied Mathematics, 2003.

[9] Philip Holmes - John L. Lumley - Gal Berkooz, Turbulence, Coherent Structures, Dynanical Systems and Symmetry, Cambridge University Press, 2008.

[10] Xiang-Sun Zhang, Neural Networks in Optimization, Springer.Science, 2000.