El método de la función de green en el cálculo del campo eléctrico bidimensional para una corriente eléctrica en una guía de onda rectangular

Artículo
Recibido el 12 de octubre de 2017/ Aceptado el 29 de noviembre de 2017

ENTORNOS, Vol. 30, No. 2, Noviembre 2017

Sergio Herrera Álvarez
Universidad Surcolombiana, Colombia
mathematical.physics@gmail.com [Link]

Jheison Lizcano Muñoz
Universidad Surcolombiana, Colombia
lizcano-fis@hotmail.com [Link]

Francis Segovia-Chaves
Universidad Surcolombiana, Colombia
francis.segoviac@gmail.com

Resumen

Las ecuaciones diferenciales aparecen frecuentemente en varias áreas de la matemática y de la física. El trabajo de George Green en 1825 sobre el método de la función de Green se ha convertido en una herramienta de la física matemática para abordar problemas que involucran ecuaciones diferenciales no-homogéneas bajo ciertas condiciones de contorno. Este método abarca problemas desde la física clásica hasta abordar complejos problemas contemporáneos de la materia condensada y teoría cuántica de campos. En este trabajo se describe de manera general el método de la función de Green para encontrar la solución de la ecuación de onda no-homogénea del campo eléctrico en una guía de onda rectangular, mediante una expansión en autofunciones.

Palabras clave: Ecuaciones diferenciales no-homogéneas, función de Green, autofunciones, guía de onda rectangular.

The method of the green function in the calculation of the two-dimensional electric field for an electric current in a rectangular waveguide

Abstract

Differential equations frequently appear in several areas of mathematics and physics; with the work of George Green in 1825, the Green function method has become a tool of mathematical physics to address problems involving non-homogeneous differential equations under certain boundary conditions. This method encompasses problems from classical physics and complex contemporary problems of condensed matter and quantum field theory. In this work, the method of the Green functions is described in general to find the solution of the non-homogeneous wave equation of the electric field in a rectangular waveguide, by means of an expansion in auto-functions.

Keywords: Non-homogeneous differential equations, Green function, auto-functions, rectangular waveguide.

Introducción

Todos los fenómenos físicos se describen mediante ecuaciones diferenciales y uno de los grandes problemas de la física se centra en resolver este tipo de ecuaciones, las cuales involucran funciones y sus derivadas, además de estar sujeta a unas condiciones de frontera (Saletan & José, 1998). Existen dos tipos ecuaciones diferenciales: las ordinarias, las cuales relacionan una función de una variable con sus derivadas y las parciales en que las variables independientes pueden por ejemplo ser las coordenadas espaciales y el tiempo (Pastor, 1988).

En el siglo XIX el matemático inglés George Green, propone un método para resolver ecuaciones diferenciales parciales nohomogéneas donde el método de separación de variables no tiene aplicación. Este método encuentra aplicación aún en los casos de ecuaciones diferenciales ordinarias homogéneas y constituye un método alternativo a los de Fourier, variación de parámetros o coeficientes indeterminados (Challis, 2003; Sepulveda, 2009). En el caso general, la función de Green es una distribución, que fue introducida por Green en el electromagnetismo, y más tarde usada por Neumann en la teoría del potencial newtoniano (Strauss, 1992) Helmholtz en acústica (Aleixo & Oliveira, 2008) y al igual que Richard Feynman en la teoría de campos cuánticos con un nombre diferente, propagador (De La Peña, 2014).

El objetivo de este trabajo es introducir a los estudiantes de ciencias y áreas afines en el método de solución de ecuaciones diferenciales en derivadas parciales no-homogéneas mediante el método de la función de Green. Se considera un problema de aplicación, en el que se propone solucionar la ecuación de onda no-homogénea la cual rige el comportamiento del campo eléctrico en una guía de onda rectangular infinita de sección transversal constante.

Metodología

Haciendo uso del método de la función de Green, calculamos el campo eléctrico generado por un alambre por el cual circula una corriente eléctrica unitaria en la sección transversal de una guía de ondas rectangular de dimensión ab. Primero describiremos el método general de solución de las ecuaciones en derivadas parciales, para luego utilizar estos resultados en la solución del problema planteado.

El método de la función de Green

Consideramos la ecuación diferencial lineal de la forma:

\hat{L} ψ (\vec{r}) = f (\vec{r})

(1)

Siendo $\hat{L}$ un operador diferencial lineal, $ψ (\vec{r})$ es la función incógnita y una función dada. Generalmente se propone resolver la ecuación (1) en un dominio D con ciertas condiciones de frontera; para $f (\vec{r})$ = 0 se tiene una ecuación diferencial homogénea (Arrken & Weber, 2005). Para resolver la ecuación (1) se multiplica por el operador inverso $\hat{L}$ ^-1, al tener en cuenta que $\hat{L}$ ^-1 $\hat{L}$ = $\hat{I}$ , siendo $\hat{I}$ el operador identidad, se obtiene

ψ (\vec{r}) = {\hat{L}}^{- 1} f (\vec{r})

(2)

con la propiedad de la función delta de Dirac (Butkov, 1968).

f (y) = \int f (y^{'}) δ (y - y^{'}) {dy}^{'}

(3)

la ecuación (2), toma la forma

ψ (\vec{r}) = {\hat{L}}^{- 1} \int f (\vec{r'}) δ (\vec{r} - \vec{r'}) d^{3} r' = \int f (\vec{r'}) {\hat{L}}^{- 1} δ (\vec{r} - \vec{r'}) d^{3} r'

(4)

Haciendo,

G (\vec{r}, \vec{r'}) = {\hat{L}}^{- 1} δ (\vec{r} - \vec{r'})

(5)

la ecuación (4) se expresa como:

ψ (\vec{r}) = \int f (\vec{r'}) G (\vec{r}, \vec{r'}) d^{3} r'

(6)

En la ecuación (5) $G (\vec{r}, \vec{r'})$ se denomina función de Green, en esta ecuación hay que considerar $\vec{r}' \in D$ como un parámetro fijo y el operador diferencial $\hat{L}$ opera sobre la variable $\vec{r}$ . En general se establece que $G (\vec{r}, \vec{r'})$ depende de dos variables: la posición $\vec{r}'$ de la fuente puntual y de $\vec{r}$ la cual señala un punto del espacio donde se estudia el efecto de la fuente. El encontrar la función de Green $G (\vec{r}, \vec{r'})$ bajo unas condiciones de frontera dadas, permite obtener la solución de la ecuación diferencial (1) por medio de la ecuación (6).

Forma bilineal de la función de Green

Para calcular la función de Green (5), se realiza una expansión de autofunciones del operador diferencial $\hat{L}$ . Para ello consideramos la ecuación de valores propios con espectro discreto,

\hat{L} \emptyset_{n} (\vec{r}) = λ \emptyset_{n} (\vec{r})

(7)

Donde $\emptyset_{n}$ y $λ$ son las autofunciones y autovalores de $\hat{L}$ , respectivamente. Si la función de Green $G (\vec{r}, \vec{r}')$ existe y si el conjunto ${\emptyset_{n} (\vec{r})}$ forma una base completa y ortogonal (Griffiths, 2016),

\sum_{n} \emptyset_{n}^{*} (\vec{r}') \emptyset_{n} (\vec{r}) = δ (\vec{r} - \vec{r}')

(8)

$G (\vec{r}, \vec{r}')$ se expande en términos de la base ${\emptyset_{n} (\vec{r})}$ , así:

G (\vec{r}, \vec{r}') = \sum_{n} a_{n} (\vec{r}') \emptyset_{n} (\vec{r})

(9)

Al multiplicar la ecuación (9) por el operador $\hat{L}$ y teniendo en cuenta la ecuación de valores propios (7), se obtiene

\hat{L} G (\vec{r}, \vec{r}') = λ \sum_{n} a_{n} (\vec{r}') \emptyset_{n} (\vec{r}) = δ (\vec{r} - \vec{r}')

(10)

donde se ha tenido en cuenta de la ecuación (5), $\hat{L} G (\vec{r}, \vec{r}') = δ (\vec{r} - \vec{r}')$ . Ahora se multiplica la ecuación (10) por $\emptyset_{n'}^{*} (\vec{r})$ e integra en todo el volumen de interés, junto con la propiedad (3) y con la ortogonalidad de las autofunciones $\int \emptyset_{n'}^{*} (\vec{r}) \emptyset_{n} (\overset{⇀}{r}) d^{3} r' = δ_{nn'}$ ; se demuestra que el coeficiente $a_{n}$ viene dado por,

a_{n} (\vec{r}') = \frac{\emptyset_{n}^{*} (\vec{r}')}{λ}

(11)

El anterior resultado se sustituye en la ecuación (9), obteniendo así la llamada forma bilineal de la función de Green (Mathews & Wlaker, 1979)

G (\vec{r}, \vec{r}') = \sum_{n} \frac{\emptyset_{n}^{*} (\vec{r}') \emptyset_{n} (\vec{r})}{λ}

(12)

Obsérvese que en la ecuación (12) que $G (\vec{r}, \vec{r}') = G^{*} (\vec{r}, \vec{r}')$ , además pone de manifiesto la dependencia de $G (\vec{r}, \vec{r}')$ con el valor propio λ, en donde debemos relacionar los polos de la función de Green con el fenómeno de resonancia (French, 1974).

Planteamiento del problema

Como un problema de aplicación, se plantea calcular el campo eléctrico generado por una línea de corriente unitaria $\vec{J}$ , que se extiende paralela al eje y de la sección transversal de la guía de onda rectangular infinita en dirección z; donde a y b representan las dimensiones transversales como se muestra en la figura 1.

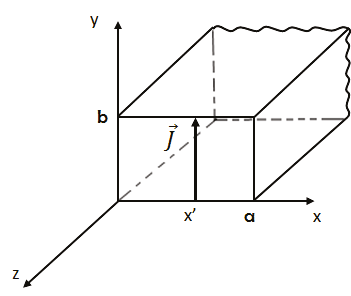
Figura 1. Línea de corriente eléctrica unitaria $\vec{J}$ en una guía de onda rectangular.

El comportamiento de los fenómenos electromagnéticos se encuentra regido por las ecuaciones de Maxwell, los campos eléctricos $\vec{E}$ y de inducción magnética $\vec{B}$ pueden calcularse mediante los potenciales electromagnéticos (Cheng, 1989):

\vec{E} = - \vec{\nabla} \emptyset - \frac{\partial \vec{A}}{\partial t}, \vec{B} = \vec{\nabla} X \vec{A}

(13)

Donde $\emptyset$ es el potencial escalar y $\vec{A}$ es el potencial vectorial magnético, los cuales satisfacen la ecuación de onda no-homogénea (Jackson, 1998):

(\nabla^{2} - \frac{1}{c 2} \frac{\partial^{2}}{\partial t^{2}}) \{\begin{matrix} \vec{A} (\vec{r}, t) \\ \emptyset (\vec{r}, t) \end{matrix}\} = - \{\begin{matrix} μ_{0} \vec{J} (\vec{r}, t) \\ \frac{ρ (\vec{r}, t)}{\in_{0}} \end{matrix}\}

(14)

En la ecuación (14), $\vec{J} (\vec{r}, t)$ y $ρ (\vec{r}, t)$ representan respectivamente las densidades de corriente eléctrica y de carga eléctrica; en lo que sigue asumiremos que estas fuentes son constantes. En el vacío la permeabilidad magnética viene representada por $μ_{0}$ y la permitividad por $\in_{0}$ , c es la velocidad de la luz. Al considerar que los campos electromagnéticos presentan una dependencia de tipo armónico respecto al tiempo, $\vec{ε} (\vec{r}) e^{iwt}$ y $\vec{B} (\vec{r}) e^{iwt}$ , los potenciales $\emptyset$ y $\vec{A}$ cumplen con la misma dependencia temporal. Por lo tanto, de la condición de Lorentz

\vec{\nabla} . \vec{A} + \frac{1}{c^{2}} \frac{\partial \emptyset}{\partial t} = 0

(15)

se encuentra que el potencial escalar viene dado por:

\emptyset = - \frac{c^{2}}{i w} \vec{\nabla} . \vec{A}

(16)

Al sustituir la ecuación (16) en (13), se obtiene

\vec{E} (\vec{r}, t) = \frac{c^{2}}{i w} \vec{\nabla} (\vec{\nabla} . \vec{A}) - i w \vec{A} (\vec{r})

(17)

Al imponer en la ecuación (17), que $\vec{A}$ satisface el gauge de Coulomb $\vec{\nabla} . \vec{A} = 0$ , el campo eléctrico toma la forma:

\vec{E} (\vec{r}, t) = - i w \vec{A} (\vec{r}, t)

(18)

la cual satisface,

\nabla^{2} \vec{E} (\vec{r}, t) = - i w \nabla^{2} \vec{A} (\vec{r}, t)

(19)

Al reemplazar en la ecuación (19), la ecuación de diferencial $\vec{A} (\vec{r}, t)$ dada por (14) y junto con (18), se demuestra que el campo eléctrico satisface la ecuación diferencial no-homogénea:

\nabla^{2} \vec{E} (\vec{r}) + \frac{w^{2}}{c^{2}} \vec{E} (\vec{r}) = i w μ_{0} \vec{J}

(20)

Donde se ha omitido la dependencia temporal del campo eléctrico, para calcular este campo se requiere resolver (20); a continuación describiremos el método de solución a partir de la función de Green.

Resultados

En la figura se presenta el problema a estudiar, por simetría, el potencial vectorial magnético tiene únicamente componente $\vec{A} = A_{y} {\hat{e}}_{y}$ con una densidad de corriente unitaria $J = δ (x - x') δ (z - z')$ . La ecuación (20) se expresa como:

\frac{\partial^{2} E_{y}}{\partial x^{2}} + \frac{\partial^{2} E_{y}}{\partial z^{2}} + \frac{w^{2}}{c^{2}} E_{y} = i w μ_{0} δ (x - x') δ (z - z')

(21)

Para solucionar (21), se considera una expansión en series de funciones ortonormales para $E_{y}$ (ver la ecuación (9)), donde se puede establecer que $E_{y}$ es la función de Green a calcular:

E_{y} (x, z) = \sum_{n = 1}^{\infty} ξ_{n} (z) \sin (\frac{n π}{a} x)

(22)

A partir de la relación de completez,

δ (x - x') = \sum_{n = 1}^{\infty} \sin (\frac{n π}{a} x) \sin (\frac{n π}{a} x')

(23)

se sustituye las ecuaciones (22) y (23) en (21), después de realizar algunas simplificaciones algebraicas se encuentra,

\frac{\partial^{2} ξ_{n} (z)}{\partial z^{2}} - {Γ_{n}}^{2} ξ_{n} (z) = i w μ_{0} \sin (\frac{n π}{a} x') δ (z - z')

(24)

donde ${Γ_{n}}^{2} = \frac{n^{2} π^{2}}{a^{2}} - \frac{w^{2}}{c^{2}}$ . Para solucionar la ecuación (24) se propone dos condiciones en los intervalos de solución:

Condición 1: $z \neq z'$

Con esta condición la función delta de Dirac es nula $δ (z - z') = 0$ , por lo tanto la ecuación diferencial (24) se escribe:

\frac{\partial^{2} ξ_{n} (z)}{\partial z^{2}} - Γ_{n}^{2} ξ_{n} (z) = 0

(25)

con una solución dada por,

ξ_{n} (z) = A_{n} e^{Γ_{n} z} + B_{n} e^{- Γ_{n} z}

(26)

Se debe tener en cuenta que las soluciones finitas de (26), existen cuando se cumple:

Para

z < z' ξ_{n} (z) = A_{n} e^{Γ_{n} z} = A_{n} e^{Γ_{n} z <}

(27)

Para

z < z' ξ_{n} (z) = B_{n} e^{- Γ_{n} z} = B_{n} e^{- Γ_{n} z >}

(28)

donde $A_{n}$ y $B_{n}$ dependen de z’. De las dos relaciones anteriores, la solución general (26), se 0expresa como:

ξ_{n} (z) = C_{n} e^{- Γ_{n} (z_{>} - z_{<})}

(29)

Condición 2: $z = z'$

Con esta condición $δ (z - z') = 0$ , para ello integramos (24) entre $z = z' \pm \in$ con $\in$ infinitesimal, $\in \to 0$

\int_{z' - \in}^{z' + \in} \frac{d^{2} ξ_{n}}{d z^{2}} d z - {Γ_{n}}^{2} \int_{z' - \in}^{z' + \in} ξ_{n} (z) d z = i w μ_{0} \sin (\frac{n π}{a} x') \int_{z' - \in}^{z' + \in} δ (z - z') d z

(30)

De la ecuación (30) se demuestra,

\frac{d ξ_{n}}{d z} z' + \in - \frac{d ξ_{n}}{d z} z' - \in = i w μ_{0} \sin (\frac{n π}{a} x')

(31)

La ecuación (31) muestra una propiedad de la función de Green, la discontinuidad en la derivada de $ξ_{n}$ . Al reemplazar en (31) la solución (29), y luego de efectuar los cálculos, se encuentra que la constante $C_{n}$ viene determinada por,

C_{n} = - \frac{i w μ_{0}}{2 Γ_{n}} \sin (\frac{n π}{a} x')

(32)

Teniendo en cuenta el resultado (32) en (29), la solución de la ecuación diferencial se escribe

ξ_{n} (z) = - \frac{i w μ_{0}}{2 Γ_{n}} \sin (\frac{n π}{a} x') \{\begin{cases} e^{- Γ_{n} (z - z')} z \geq z' \\ e^{- Γ_{n} (z' - z)} z \leq z' \end{cases}

(33)

En definitiva, al sustituir la ecuación (33) en (22) se encuentra la solución de (21) para la geometría del problema planteado,

E_{y} (x, z; x', z') = - \frac{i w μ_{0}}{2} \sum_{n = 1}^{\infty} \sin (\frac{n π}{a} x') \sin (\frac{n π}{a} x) \frac{e^{- Γ_{n} |z - z'|}}{Γ_{n}}

(34)

El resultado obtenido presenta una simetría $E_{y} (x, z; x', z') = E_{y} (x', z'; x, z)$ . Además, cuando $\frac{w}{c} = \frac{n π}{a}$ para algún entero n, $E_{y} (x, z; x', z')$ , no existe. Por lo tanto se puede decir que el campo eléctrico (función de Green) posee polos simples para $Γ_{n} (n = 1, 2, . . .)$ . Desde el punto de vista físico el hecho que $E_{y} (x, z; x', z')$ no exista, es un claro ejemplo de resonancia donde $w_{n} = \frac{n π}{a} c$ . Es decir, la frecuencia de oscilación del campo alcanza una de las frecuencias características de oscilación de la guía.

Conclusiones

La función de Green es un método para solucionar problemas que involucren ecuaciones diferenciales no-homogéneas bajo ciertas condiciones de contorno, siendo ésta función, independiente del término no homogéneo en la ecuación diferencial. Una de las propiedades que presenta la solución es la de simetría. Si bien es un método de solución elegante, presenta cierta complejidad ya que no siempre es posible encontrar soluciones explicitas para la función de Green por estar en términos del delta de Dirac y adicionalmente de las condiciones de contorno que se debe satisfacer.

En este trabajo presentamos la derivación de la función de Green relativa a la ecuación de onda no-homogénea del campo eléctrico en el espacio bidimensional. Para ello, se propuso la expansión en funciones ortonormales del campo eléctrico, obteniendo finalmente la solución representada por la ecuación (34), similar a la forma bilineal que se muestra en la ecuación (12). Se demostro además la propiedad de simetría y la existencia de polos simples en la solución obtenida.

Reconocimientos

Los autores agradecen a la Universidad Surcolombiana por la financiación del Proyecto del Semillero de Física Matemática titulado: Cálculo de la función de Green para sistemas disipativos mecánicos y electromagnéticos, febrero del 2017.

Referencias Bibliográficas

Aleixo, R., & Oliveira, E. (2008). Green's function for the lossy wave equation. Rev. Bras. Ensino Fis., 30, 13021-13025.

Arrken, G., & Weber, H. (2005). Mathematical methods for physicists international student edition. Academic press.

Butkov, E. (1968). Mathematical Physics. Massachusetts: Addison wesley.

Challis, L. (2003). The green of green functions. Physics Today, 41-46.

Cheng, D. (1989). Field and wawe electromagnetics. New York: Addison-Wesley.

De La Peña, L. (2014). Introduccion a la mecánica cuántica. Fondo de Cultura Económica.

French, A. P. (1974). Vibraciones y Ondas. Mexico: Reverte S.A.

Griffiths, D. (2016). Introduction to quantum mechanics. Cambridge University Press.

Jackson, J. (1998). Classical Electrodynamic. Jhon Wiley and Sons.

Mathews, J., & Wlaker, R. (1979). Matemáticas para físicos. Barcelona: Reverté.

Pastor, J. R. (1988). Los problemas lineales de la Física. CSIC-CSIC Press.

Saletan, J., & José, J. (1998). Classical Dynamics: A contemporary approach. Cambridge: Cambridge University Press.

Sepulveda, A. (2009). Física matemática. Medellin: Universidad de Antioquia.

Strauss, W. (1992). Partial differential equations (Vol. 92). New York: Wiley.