Enero-Diciembre 2019;4(1): 84-97
CÁLCULO DEL ESPESOR Y LA TRANSMITANCIA EN PELÍCULAS DELGADAS DE MATERIALES FOSFURO DE INDIO-GALIO-ARSÉNICO (InGaAsP) Y FOSFURO DE INDIO (InP) EN LA ESTRUCTURA DE UN SISTEMA ÓPTICO UNIDIMENSIONAL
CALCULATION OF THICKNESS AND TRANSMITTANCE IN THIN FILMS OF INDIUM-GALLIUM-ARSENIC PHOSPHIDE (InGaAsP) AND INDIUM PHOSPHIDE (InP) IN THE STRUCTURE OF A ONE-DIMENSIONAL OPTICAL SYSTEM
Luis Jojoa-Losada
Francis Segovia
Resumen
En este trabajo se determina el espesor de las películas delgadas formadas por los materiales fosfuro de indio-galio-arsénico y fosfuro de indio, con el propósito de determinar la transmitancia en la región del espectro visible y la zona infrarroja más intensa. Para ello se hace uso de dos “análogos”, el cuántico, a partir del cual se modela el comportamiento de una partícula energética confinada en un pozo de potencial finito, y se determina la transmitancia a través del método de la matriz de transferencia. El otro análogo, el electrodinámico, describe la propagación de una onda electromagnética con polarización tipo (TE) a través de una estructura unidimensional conformada por cada una de las películas delgadas de los materiales tratados en este trabajo. Se calculó la transmitancia haciendo uso de la ecuación de Helmholtz, de las condiciones de frontera y de continuidad de la función de onda en cada una de las interfases. Finalmente, fue necesario calcular el espesor de los materiales, para lo cual se hizo uso de la óptica geométrica y la ley de Snell. Conocidos los espesores, se obtienen los resultados de la transmitancia para cada una de las películas delgadas, concluyéndose finalmente que, si la magnitud de las longitudes de onda es próxima a los espesores de las películas delgadas, se obtienen resultados con transmitancia constante, y si las magnitudes de las longitudes de onda son mayores a la de los espesores, se presenta un decaimientoen la transmitancia del material.
Palabras clave: Espesor, Transmitancia, Espectro.
Abstract
In this work, we determine the thickness of thin films formed by the materials indium-gallium-arsenic phosphide and indium phosphide, to determine the transmittance in the visible spectrum region and the most intense infrared zone. For this purpose, we use two ”analogs”. The quantum one, from which the behavior of an energy particle confined to a finite potential well is modeled, and the transmittance is determined through the transfer matrix method. The other analog, the electrodynamic, describes the propagation of an electromagnetic wave with polarization type (TE) through a one-dimensional structure formed by each of the thin films of the materials treated in this work. We calculated transmittance using the Helmholtz equation, the boundary and continuity conditions of the wave function in each of the interfaces. Finally, it was necessary to calculate the thickness of the materials, using geometric optics and Snell’s law. Known thicknesses, the transmittance results are obtained for each of the thin films, concluding that, if the magnitude of the wavelengths is close to the thicknesses of the thin films, results are obtained with constant transmittance. If the magnitudes of the wavelengths are greater than those of the thicknesses, there is a decay in the material’s transmittance.
Keywords: Thickness, Transmittance, Spectrum
Introducción
Los materiales conocidos como fosfuro de indio y fosfuro de indio-galio-arsénico son excelentes semiconductores, y de importante aplicabilidad en el campo de la fotónica, tal como lo exponen Miao, P., Zhang, Z., Sun, J., Walasik, W., Longhi, S., Litchinitser. N. y Feng. Estos materiales son usados en la fabricación de láseres con luz helicoidal (Miao, P. et al, 2016), a la vez que son especialmente utilizados en la fabricación de eficaces nanoemisores de luz, como lo son láseres de cristales fotónicos, guías de onda nanoestructuradas y sensores ópticos (Postigo et al, 2006). Según Liu K., Wang L., Zhang C., Ma Q. y Qi B., también son usados en aplicaciones tales como los interruptores fotónicos que funcionan a gran velocidad, elaborados con base en el uso de la matriz de transferencia. (Liu et al, 2018)
Con el fin de contribuir a esta variedad de aplicaciones, el propósito del estudio referenciado aquí es obtener el espesor y la transmitancia de los materiales antes mencionados en un rango espectral que abarca de los 400 a los 2000 nm, con el interés de que el espesor debe ser adecuado, a fin de lograr los máximos valores posibles de transmitancia. Por lo tanto, se pretende comprobar que, para cada rango de frecuencias, debe haber valores propicios de espesores en las películas delgadas, para que haya fenómenos de transmitancia.
Para comprobar esta afirmación, se consideran dos modelos, el modelo electrodinámico, explicado en el ítem 2.1, y el modelo cuántico, descrito en el ítem 2.2. Luego, siguiendo estos modelos, se determina el espesor apropiado para las películas delgadas de los materiales estudiados, haciendo uso de la ley de Snell y la óptica geométrica. Conocidos ya los espesores, se determina la transmitancia en el rango del espectro visible, y la zona infrarroja más intensa para cada modelo, haciendo uso del método de la matriz de transferencia.
Los resultados fueron obtenidos en el software de cálculo Wólfram Mathematica, obteniéndose los resultados ilustrados en las figuras 3 y 4, los cuales permiten comprobar que el espesor apropiado para una óptima transmitancia en la película delgada del fosfuro de indio-galio-arsénico es de 1235 nm, mientras que en el fosfuro de indio el espesor ideal es de 1500 nm en el rango de 400-2000 nm del espectro visible, y de mayor intensidad en el infrarrojo. Además, se comprobó mediante el espectro, en la escala que va desde 0.4-1000* 103 nm, en comparación con la escala que va desde de [0.4-2]*103 nm, que la posibilidad de que haya transmitancia es debido a que los espesores de las películas son próximos o menores a las magnitudes de longitudes de onda. Por otro lado, se obtuvo, en el caso de un pozo de potencial doble y finito, que los fenómenos de transmitancia son posibles cuando la energía de las partículas confinadas en un pozo de potencial son mayores a la energía de un pozo y una barrera de potencial.
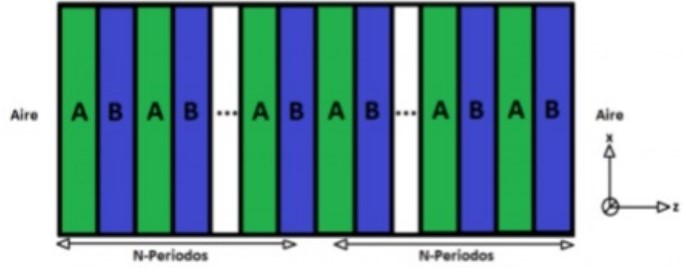
Figura 1. Representación de del modelo periódico de N-capas alternadas con los materiales (A) y (B), y de la incidencia de una onda electromagnética con polarización de la forma TE
Metodología
Con el propósito de determinar el espesor de las películas delgadas de los materiales fosfuro de indio-galio-arsénico (InGaAsP) y Fosfuro de indio (InP), y procurando que estos espesores sean propicios a valores máximos de transmitancia dentro del rango del espectro infrarrojo, se plantean dos modelos mediante los cuales sea posible analizar esta propiedad. Estos modelos se rigen bajo leyes o principios en distintos campos de la física y son conocidos como análogos físicos. Uno de estos es el análogo clásico electrodinámico, en el que se hace uso de la ecuación de Helmholtz [Ecuación 1]
(∇2 − k∈)ψ = 0
Esta ecuación, como lo manifiesta Peña (2014), contiene la constante “dispersión electromagnética”, portadora de la información física de propagación, definida, según lo afirmado por French A. (2006) como T = 2π/w, de dónde se puede de decir que w = 2πc/λ. Seguidamente, se prosigue a evaluar las condiciones de frontera y continuidad de la función de onda en cada uno de los límites del medio trifásico Aire/InGaAsP/nP, como se ilustra en la figura 2. Finalmente, mediante la continuidad de los campos eléctricos y magnéticos, se llega a la expresión de la transmitancia [Ecuación 2] para una onda electromagnética con polarización tipo TE, en un sistema óptico periódico unidimensional.
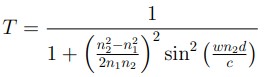
2.1 Planteamiento del modelo electrodinámico
En este modelo se utiliza la representación del esquema utilizado por Segovia y Vinck (2018), el cual se ilustra en la figura 1 (Segovia et al, 2018). En el modelo que se emplea en este trabajo no es necesario incluir un modo defecto, y la representación de este modelo se puede ver en la figura 2
De esta manera, su estructura es “Aire/InGaAsP/InP/Aire”, en las regiones I, II y III respectivamente, con índices de refracción, según lo expuesto por Seifert S. y Runge P., de n1 = 1.26 y n2 = 3.7 para energías de (0.73 eV.), concernientes al material (InGaAsP)
Según lo expuesto por Kikuno E., Amiotti M., Takisawua T., y Arai S., (n3 = 3.1), para el material (InP), puede verse claramente que, en este orden, la alternancia se da entre las capas A y B, conformándose la estructura , “Aire/AB/AB/Aire”, donde (A) es el material InGaAsP y (B) el material InP. De esta forma, se presenta una periodicidad unidimensional. Tal como lo define Ibisate (2003), un sistema óptico periódico y unidimensional es aquel que se compone de capas de distinto material alternadas en una dirección. Sin embargo, en este trabajo, únicamente se tratará de evaluar el comportamiento de la transmitancia en las tres primeras regiones de la estructura de N-capas periódicas
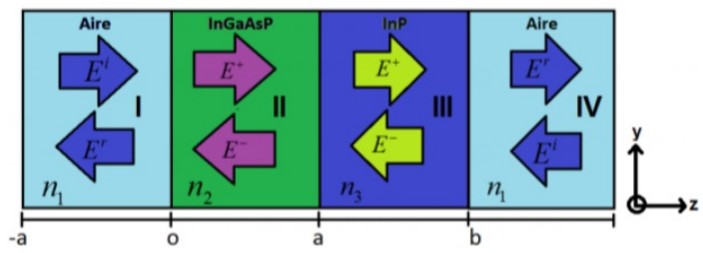
Figura 2. Representación esquemática de las tres primeras capas de un sistema óptico unidimensional de N-capas y polarización de la onda tipo TE, a través de cada uno de los materiales, en la forma aire/InGaAsP/InP/Aire, con índices de refracción n1, n2 y n3 en las regiones (I, II, III, y IV)
2.2. Modelo cuántico
Por otro lado, según lo propuesto por Mayorga A., De Broglie, Einstein y Schrödinger (1923-1925), la energía de un haz de luz puede expresarse como valores discretos a los cuales Einstein denomino fotones. Sumado a ello, D’ Broglie (1910) postuló el principio de dualidad onda partícula. Por lo tanto, el análogo cuántico toma la representación del fotón del modelo electrodinámico como una partícula, confinada en algún pozo de potencial. Este pozo hace parte de una estructura más compleja, como lo afirman Wysozka J. y Mendoza F.
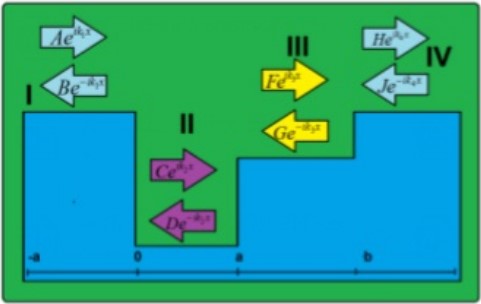
Figura 3. Estructura de pozo de potencial doble con amplitudes incidentes y reflejadas en las regiones (I,II, III y IV), con espesores (-a, 0, a y b) en analogía con cada uno de los materiales (InGaAsP) y (InP).
Bajo este método se puede representar un doble pozo de potencial finito, el cual puede estar conformado por pozos y barreras de potencial consecutivos (Wysozka et al, 2016). Esta forma de pozo de potencial se ilustra en la figura 3, la cual representa la primera parte de una estructura que se repite consecutivamente (N) veces, las que sean necesarias para que se forme la periodicidad de la constante cuántica. Esta estructura que se repite, y como se sabe, es un doble pozo de potencial y, debido a que no son iguales, forman, a partir de las fronteras, barreras de potencial, donde cada parte conforman las regiones (I, II, III y IV) respectivamente.
Tras este procedimiento, se solucionar la “ecuación de Schrödinger [Ecuación .3], con la finalidad de obtener la transmitancia. Acto seguido, se aplican las condiciones de frontera y de continuidad de la función de onda para, finalmente, obtener la matriz de
transferencia [Ecuación. 4.] y la transmitancia como el inverso cuadrado del primer elemento de la diagonal principal [Ecuaciones 5 y 6].
(∇2 − ke)ψ = 0
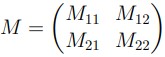
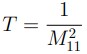
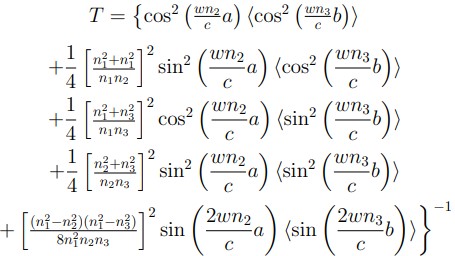
Según lo expone Acosta (1999), la partícula describe valores discretos de energía dentro de los límites de un potencial atractivo que la confina. En estas condiciones, si la partícula es estimulada por radiación con energía lo suficientemente grande, esta se ubicará a diferentes alturas del pozo, en orden de diferentes valores discretos de energía cada vez más grandes, hasta alcanzar la energía suficiente para llegar al estado de partícula libre. Por otro lado, si la energía de la partícula es muy grande, al punto de superar el valor de la energía de la barrera que le sigue, efecto túnel tomaría lugar y, por lo tanto, habría transmitancia. En estos dos fenómenos, a la relación de energía perdida o ganada por la partícula, y la energía del pozo o barrera de potencial, se le denomina coeficiente de relación de energía, el cual puede ser introducido, tal como lo presentan Rivas, Castiblanco y Morales (2012), en la transmitancia; en función de las variables opacidad del pozo de potencial y coeficiente de relación de energía, [Ecuación 8], con x = (2a/h) √2mV como la opacidad del pozo o barrera de potencial, cuyo valor depende de la masa de la partícula, cantidad de energía potencial, y la relación de energía dada como η = E/V .
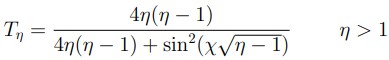
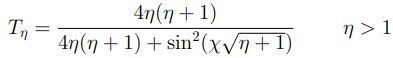
2.3. Espesores de las películas delgadas
Es necesario, para concretar correctamente los resultados, conocer la longitud de los espesores. Con este fin, se hace uso de la teoría sencilla de la óptica geométrica, específicamente de la “ley de Snell” , que retoma los temas tratados por los autores Jenkins F. y White H., (1964). La ley de Snell describe el comportamiento y las propiedades de velocidad y longitud de onda, en función de los índices de refracción, cuando un rayo de luz se propaga entre dos medios materiales, entendiéndose la refracción como el cambio en la dirección del rayo de luz respecto a la normal en la frontera entre los materiales. Ahora, aplicando esta ley en los tres primeros medios del modelo electrodinámico para una difracción de orden (m), es posible obtener el ángulo de refracción en el medio 2, cuando el rayo de luz pasa desde el aire al material de fosfuro de indio-galio-arsénico (InGaAsP), el cual será utilizado para determinar el espesor del material fosfuro de indio (InP). Seguidamente, habiendo conocido el ángulo de incidencia del primer medio (aire, en este caso) y el ángulo de refracción del medio dos, es posible hacer uso de lo propuesto por Jenkins y White (1964), acerca de “espesores y película delgadas”, quienes determinan la expresión para máximos en longitudes de onda, producidos por interferencia constructiva después de que un rayo de luz incide y penetra una película de espesor (a). (Ecuación 9).
ni sinθi = nj sinθj
Donde ni , nj , θi y θj son los índices y ángulos de incidencia y de refracci´on respectivamente en los medios materiales InGaAsP e InP. Ahora, considerando que el ángulo de incidencia es igual al ángulo de refracción en un mismo medio material, puede definirse la ecuación para el espesor de la placa (Ecuación 10).
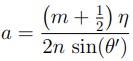
Donde (m) es el orden de difracción, (n) es el índice de refracción del medio material, (η) la longitud de onda y (θ') el ángulo de refracción del medio material. Finalmente, conocida ya la expresión, que permite determinar los espesores de las películas delgadas, puede ser evaluada la transmitancia en cada medio material
Con la finalidad de determinar la transmitancia en las películas de los materiales propuestos con índices de refracción de (n1 = 3.7) y (n2 = 3.1) respectivamente, se determinó el espesor apropiado, definido como el par´ametro que se relaciona al rango del espectro visible y de mayor intensidad en el infrarrojo (400-2000 nm). Además de ello, se determina lo que ocurre con la transmitancia para longitudes de ondas en el rango del espectro de (2000 − 2 ∗ 107nm), los cuales se ilustran en la gráfica de la figura 1
a)
b)
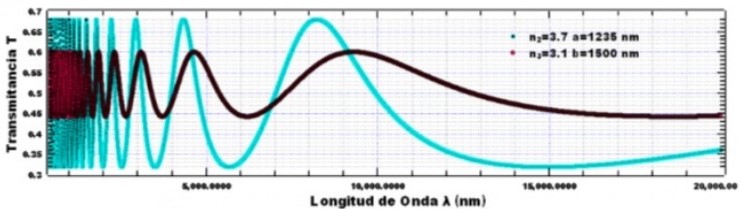
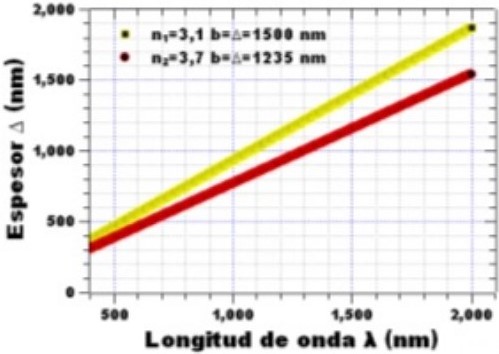
Figura 1. a) Material (InGaAs) con coeficiente de refracción n2 = 3.7 y espesor apropiado ∆ = a = 1235nm y material (InP) con índice de refracción n3 = 3.1 y espesor apropiado ∆ = b = 1500nm. b) transmitancia para el material (InGaAs) con n2 = 3.7 y espesor apropiado ∆ = a = 1235nm y transmitancia para el material (InP) con n2 = 3.1 y espesor apropiado ∆ = b = 1500nm
El delta en la figura 1.a representa el valor del espesor apropiado para cada material. De esta manera, dicho valor para el material fosfuro de indio-galio-arsénico (InGaAsP) es de 1235 nm, el cual se comprende como el intervalo que va desde el punto mínimo con longitud de onda (400 nm) al punto máximo con longitud de onda (2000 nm). Además, cada longitud de onda del espectro tratado aquí está dentro del rango 315-1550 nm.
De igual manera, el espesor apropiado para el fosfuro de indio (InP) está dentro del parámetro (375 − 1875nm), y su espesor es de 1500 nm. También puede verse, claramente, que estos parámetros tienen valores muy próximos en relación con el de las longitudes de onda del espectro visible, y la zona de mayor intensidad en el infrarrojo. Por lo tanto, se propone que el espesor de la película delgada del material fosfuro de indio-galio-arsénico debe ser de (∆ = 1235nm), y para el material de fosfuro de indio (InP) de (∆ = 1500nm), por lo que, de esta forma, se posibilita una alta transmitancia. Por lo contrario, cuando las longitudes de onda son mucho mayores que cualquiera de los espesores de cada material, los valores de la transmitancia decaen. Ver figura (2-b).
a)
b)
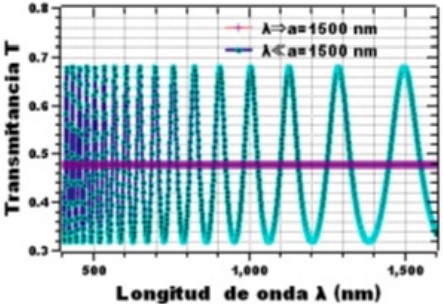
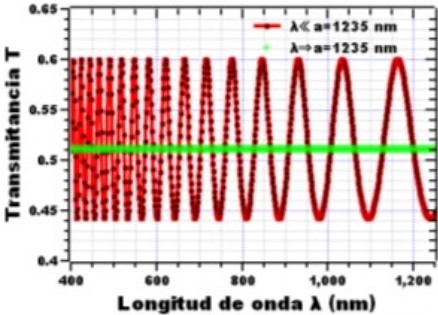
Figura 1. a) Material (InGaAs) con coeficiente de refracción n2 = 3.7 y espesor apropiado ∆ = a = 1235nm con transmitancia constante para λ −→ ∆ y interferencia para λ << ∆. b) Material (InP) con coeficiente de refracción n3 = 3.1 y espesor apropiado ∆ = a = 1235nm con transmitancia constante para λ −→ ∆ e interferencia para λ << ∆.
En consideración de los espesores encontrados como medidas apropiadas para evaluar la transmitancia, se obtienen los resultados para cada material, los cuales están expuestos en las gráficas de las figuras (2.a) y (2.b).
Puede verse que la transmitancia para el material Fosfuro de indio-galio-arsénico (InGaAsP) presenta un leve cantidad mayor de transmitancia que la del material fosfuro de indio (InP), alcanzando picos máximos de 0.7 y picos mínimos próximos a 0.3 , en comparación con la del fosfuro de indio (InP), que presenta picos máximos de (0.48) y mínimos de ( 0.3), en una escala de (0-1) en relación al rango del espectro (400-2000 nm). En otras palabras, hay una mayor transmisión del espectro en el material fosfuro de indio-galio-arsénico. Este hecho se verifica al comparar la transmitancia constante de cada material, la cual resulta con una diferencia de 0,03.
Ya se sabe que el hecho de que haya interferencia obedece a que las longitudes de onda son menores al valor de los espesores (λ = 1500nm–1235nm), y si la transmitancia es constante, y si las magnitudes de las longitudes de ondas son próximas a las magnitudes de los espesores (λ = 1500nm–1235nm), puede demostrarse que hay una mayor interferencia, y una mayor transmitancia.
Esto se verifica al comparar los valores de los picos máximos y mínimos de las figuras (1b) y (2), a medida que las longitudes de onda son muy grandes próximas a 100.000.000 nm, el número de picos máximos y mínimos disminuye, y hay menos interferencia, por lo que la transmitancia decae. Por el contrario, si las longitudes de onda son menores a los espesores de las películas, hay una gran interferencia y la transmitancia se mantiene. Ver figura (2). Sin embargo, si la longitud de onda es igual al espesor de la placa, la transmitancia se mantiene constante tanto para el fosfuro de indio galio-galio-arsénico, con un valor de 0.51, como para el fosfuro de indio, que tiene un valor de 0.4.
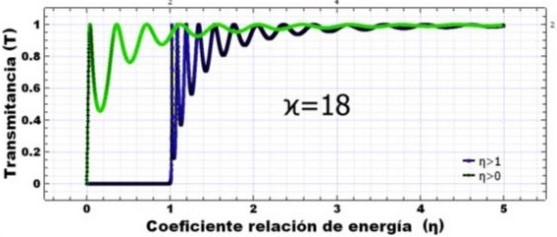
Transmitancia en un pozo de potencia con coeficientes de relación de energía (η > 1) y (η > 0) en el rango de (1-5), con opacidad de la barrera de potencial (χ = 18). Con energía del pozo de potencial de (0.1µeV )
Pueden verse las películas delgadas de materiales (InGaAsP), e (InP) con espesor de 1500 nm cada una , como un pozo y una barrera de potencial respectivamente, con cierta opacidad de 18 proporcional a un potencial de (0.1µeV ), una cantidad de energía mucho menor a la energía de radiación electromagnética en el rango del espectro visible e infrarrojo de mayor intensidad, la cual está entre ([10 y 50] eV). Por lo tanto, dado a que estas energías son mayores, existe una interferencia fabry-perot en el caso del pozo de potencial, y una transmitancia en el caso de la barrera de potencial. En ambas situaciones sucede que, cuando la energía de la partícula es mayor a la energía del pozo y la barrera de potencial, ocurre el fenómeno conocido como interferencia de “efecto túnel”, por lo tanto, como se ilustra en la [figura 7], los coeficientes de energía mayores que cero y uno (η > 0; 1) indican que hay transmitancia en una cantidad próxima a la máxima del cien por ciento (100%).
Conclusiones
Finalmente, se determinó que el espesor apropiado para una óptima transmitancia en la película delgada del material fosfuro de indio-galio-arsénico, es de 1235 nm, y en el material fosfuro de indio es de 1500 nm en el rango de ([400-2000] nm) del espectro visible de mayor intensidad en el infrarrojo. Además, se comprobó, mediante el espectro, en la escala que va desde ([400-1000000] nm) en comparación con la escala que va desde de ([400-2000]nm), que la posibilidad de que haya transmitancia es debido a que los espesores de las películas son próximos o menores a las magnitudes de longitudes de onda. Por otro lado, se obtuvo en el caso de un análogo cuántico, que los fenómenos de transmitancia son posibles cuando la energía de las partículas confinadas en un pozo de potencial es mayor a la energía de un pozo o una barrera de potencial.
Bibliografía
Acosta, V. Cowan, C., y Graham, B., H. (1999). Curso de física moderna. Recuperado de https://www.academia. edu/8570141/Acosta_Virgilio_-_Curso_De_Fisica_Moderna [link]
French A. (2006). Interferencias producidas por una doble rendija. En Massachusetts Institute of Tecnology (Ed.), Vibraciones y Ondas (314-318). New York, EEUU, Editorial Reverté S.A.
Ibisate, M. (2003). Cristales fotónicos basados en ópalos (trabajo de grado para optar a grado de doctor en ciencias). Universidad Autónoma de Madrid. Madrid.
Jenkins, F. y White, H. (1964). Interferencias por reflexiones múltiples. En Aguilar, S. A. (Ed.), Fundamentos de óptica (pp. 280-383)
Kikuno E., Amiotti M., Takisawua T. y Arai S. (1995). Anisotropic refractive index
Liu K., Wang L., Zhang C., Ma Q. y Qi B. (2018). Compacto InGaAsP/InP sin bloqueo 4x4 basado en acoplador de zanjas Mach-zehnder tejido de interruptor fotónico. OSA. Opplied Optics (57). 3838-3846.
Mayorga A., De Broglie, Einstein y Schrodonger (1923-1925). La dualidad onda-partícula y el nacimiento de la mecánica cuántica. Tecnología en marcha (14). 69-89.
Miao, P., Zhang, Z., Sun, J., Walasik, W., Longhi, S., Litchinitser. N. y Feng (29-Julio 2016). Orbital Angular Momentum microlaser. Science (533), 464-467.
Peña. L, (2014). Introducción a la mecánica cuántica. Recuperado de https://es.scribd.com/doc/306968601/Introduccion-a-la-mecanica-cuantica-luis-de-la-peA-a
Postigo P. A., Alija, A. R., Martinez L., J. y Sánchez J. (2006). Fabricación y caracterización de cristales fotónicos para nuevos dispositivos optoelectrónicos. Óptica pura y aplicada 39 (2) 185-188
Segovia, F., Vinck, H., (2018). Dependence of the defect mode with temperature, pressure and angle of incidence in a 1D semiconductor - superconductor photonic cristal. Superconductivity and it’s aplications 553, (1-7).
Seifert S. y Runge P. (2016) Revised refractive index and absorption of In1-xGaxAsyP1-y lattice-matched to InP in transparent and absorption IR-region. OSA, Óptical Materials Express 6.(2).
Wysozka J. y Mendoza F., (2016). Simetrías en la naturaleza de efecto túnel: breve estudio de pozos cuánticos dobles. Revista Mexicana de Física (62). (2016). 86-95.