Enero-Diciembre 2018;2(1): 63-69

ESTUDIO CUALITATIVO DEL MODELO MATEMÁTICO DE UN RIÑÓN ARTIFICIAL

Cindy Lorena Salas Valencia¹

Henry Medina Cruz²

Julián David Flórez Yagüe³

Yineth Medina Arce⁴

Resumen

En este trabajo presentamos dos modelos matemáticos que contribuyen al estudio del comportamiento de un riñón artificial. Los modelos utilizados corresponden a una ecuación diferencial ordinaria de primer orden y a un sistema de ecuaciones diferenciales ordinarias lineales, que permiten predecir el comportamiento del riñón artificial en pacientes con insuficiencia o falla renales.

Palabras clave: Modelo matemático, Hemodiálisis, Urea, Creatina, Acido úrico.

Abstract

In this research we present two mathematical models that contribute to the study about the behavior of an artificial kidney. The models used correspond to a first order differential equation, and a linear ordinary differential equation allowing to predict the behavior of the artificial kidney in renal impairment or complete failure patients.

---

¹ Estudiante del programa de Matemática Aplicada de la Universidad Surcolombiana

² Estudiante del programa de Matemática Aplicada de la Universidad Surcolombiana

³ Estudiante del programa de Matemática Aplicada de la Universidad Surcolombiana

⁴ Estudiante del programa de Matemática Aplicada de la Universidad Surcolombiana

---

Introducción

En este trabajo empleamos un modelo de naturaleza determinística para estudiar el funcionamiento de un riñón artificial, estableciendo una relación directa con el funcionamiento de un riñón en el cuerpo humano. Se establecen diferencias entre los modelos matemáticos existentes para explicar el funcionamiento del riñón artificial, a partir de un análisis según su funcionalidad y complejidad. Igualmente, se describen las variables y parámetros que intervienen en la formulación de cada uno modelos matemáticos propuestos. Los modelos empleados permiten estudiar la evolución de un paciente con insuficiencia renal o casi nula.

Los modelos matemáticos corresponden, específicamente, a una ecuación diferencial, y a un sistema de ecuaciones diferenciales lineales en tiempo continuo, ambos de amplia utilidad en diversos campos del conocimiento (como es el caso de la biología, la medicina, ingeniería, entre otras), para predecir el comportamiento de sistemas bajo condiciones de incertidumbre a través del tiempo. Igualmente, la utilización de estos modelos ha resultado adecuada para modelar la dinámica de poblaciones para la toma de decisiones.

En cuanto a las aplicaciones de los modelos matemáticos en el ámbito de la salud, se puede mencionar que el primer modelo matemático fue el trabajo de Daniel Bernoulli contra el sarampión. [7] Su trabajo contenía la idea de mortalidad diferencial para estimar la tasa de muerte asociada a una enfermedad. Subsecuentemente, los primeros cimientos de la epidemiología matemática se hicieron a principios del siglo XX por los médicos en salud pública y biólogos, P.D. Enko, W.H. Hamer, J. Brownlee, Sir R. A. Ross, A.G. McKendrick y W.O. Kermack. El modelo de Ross, en malaria, es tal vez uno de los acontecimientos más importantes en la historia de la epidemiología matemática.

Más adelante, Wolf y sus colaboradores fueron los primeros en describir la cinética de la diálisis y el aclaramiento del dializador, hace casi 50 años. Renkin también fue un pionero en la descripción matemática de la diálisis, mientras que Sargent y Gotch introdujeron con éxito el modelo de un compartimento para la práctica clínica a fines de los años setenta. [3] Los beneficios y riesgos de este modelo de aplicación se han descrito y discutido en muchos artículos clínicos y teóricos. A continuación, describimos algunos detalles y resultados alcanzados. Finalmente, enumeramos las principales conclusiones de este trabajo.

¿Qué es un modelo matemático?

La definición general es que un modelo matemático es un sistema dinámico ocupado para estudiar procesos iterativos de naturaleza determinística o aleatoria que corresponde a los modelos probabilísticos. Todo proceso tiene ocurrencia en su propio tiempo, que puede ser discreto o continuo. Definiéndolos, los modelos discretos son los que recorren los números enteros, mientras que los modelos continuos son los que recorren los números reales, y también tiene propósitos (puntos de equilibrio, atractores o ciclos limites o toros).

Los procesos se caracterizan por variables y/o parámetros los cuales interactúan mediante relaciones funcionales (funciones) que pueden ser lineales o no lineales.

En el lenguaje matemático, un sistema dinámico o modelo matemático, es una tripla (X,f,t), donde el conjunto X es el ambiente del sistema, la función f va del espacio de estados X en sí mismo, y se denomina ley de transición de estados µ o operador de evolución del sistema, y t es la variable temporal.

2. Funcionamiento de una máquina de diálisis:

El funcionamiento de una máquina de diálisis es el siguiente:

La sangre del paciente circula a lo largo de una membrana a una velocidad fija, mientras que, al mismo tiempo, un líquido purificador atrae las impurezas en la sangre, y la tasa de cambio de las impurezas sigue la ley de Fick, la cual afirma que la cantidad de material de desecho que pasa por una membrana es proporcional a la diferencia de concentración a un lado y otro de la misma.[8]

Con base en esta premisa, tomamos dos modelos, de los cuales, uno está dado por una ecuación diferencial, al que realizamos su respectivo análisis, y el otro es un sistema de ecuaciones, que también fue debidamente analizado. En ambos modelos analizamos sus puntos de equilibrio, y elaboramos sus respectivos planos de fases.

2.1 Definición de diálisis

En términos generales, el proceso de diálisis implica el movimiento bidireccional de las moléculas a través de una membrana semipermeable. Clínicamente, este movimiento tiene lugar dentro y fuera de la sangre, a través de una membrana semipermeable. [4] Si la sangre se expone a una membrana artificial fuera del cuerpo, el proceso se llama hemodiálisis (HD) o hemofiltración (HF), por el contrario, si el intercambio de moléculas ocurre a través de la membrana peritoneal, el proceso se llama diálisis peritoneal (PD). [1]

2.2 Mecanismos involucrados en el movimiento molecular

El movimiento de las moléculas sigue ciertos principios fisiológicos y fisicoquímicos que se describen a continuación. [1]

Principios de diálisis

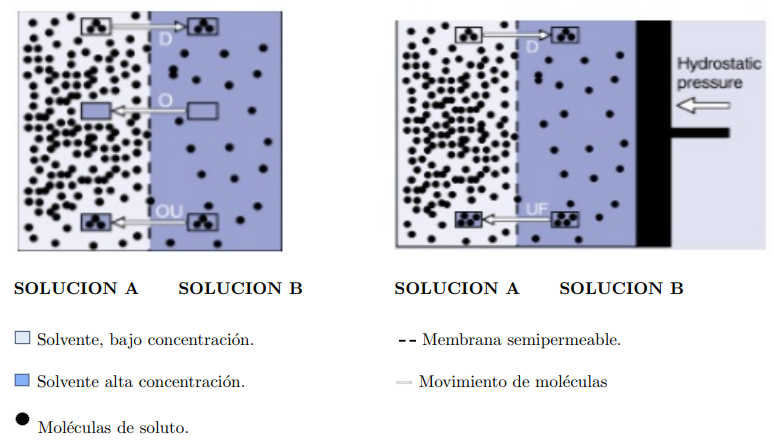
Fig. 1.1 a Difusión, ósmosis y ultrafiltración osmótica por presión osmótica. b Ultrafiltración hidrostática. Difusión D, osmosis O, ultrafiltración osmótica OU, ultrafiltración UF por hidrostática presión, convección C.[1]

3. Modelo matemático de un riñón artificial representado por una ecuación diferencial.

La sangre, que tiene una concentración de desechos u(t) (creatina, urea,) [3] al circular por la membrana que la separa del dializador, elimina una parte de las impurezas que pasan al dializador cuya concentración es v(t), y la constante k son los litros de sangre. La ecuación diferencial que modela la esta situación es

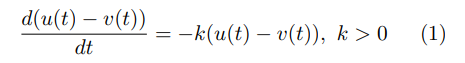
Aplicando separación de variables a (1) se obtiene:

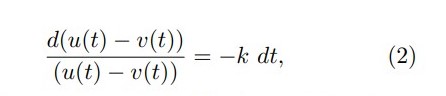
Integrando a ambos lados de la igualdad de (2):

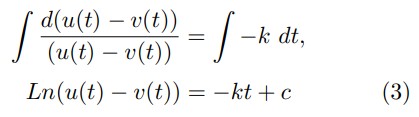
Aplicando Euler a ambos lados de la igualdad (3) obtenemos:

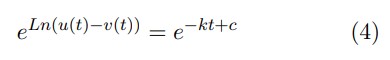
Luego, aplicando propiedades de Euler a (4), se tiene la solución del modelo Matemático del Riñón Artificial, lo que permite calcular la cantidad de material de desecho removido de la sangre por unidad de tiempo.

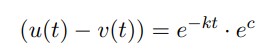
Así, la solución de la Ecuación Diferencial que Modela el Comportamiento del Riñón Artificial es

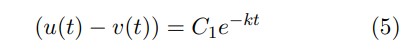
3.1 Análisis de estabilidad:

Hallando los puntos de equilibrio, tomamos el campo vectorial de la ecuación diferencial y lo igualamos a cero, es decir:

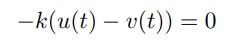
A continuación, despejamos u(t) − v(t) , y nos queda el siguiente punto de equilibrio

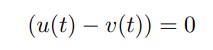
En el siguiente gráfico, se muestra la línea de fase y un esbozo de las curvas solución d(u(t)−v(t)) / dt = −k(u(t) − v(t)), teniendo en cuenta el teorema de existencia y unicidad de soluciones.

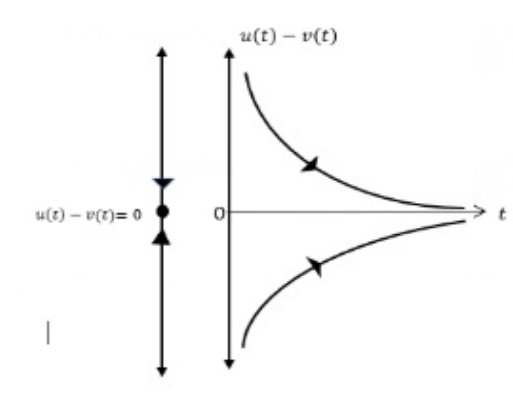
El siguiente gráfico, se muestra la línea de fase y curvas solución para d(u(t)−v(t)) / dt = −k(u(t) − v(t))

Un análisis previo del plano de fase anterior es:

* Sí t −→ ∞⁺, la concentración restante de desechos e impurezas tiende a cero, es decir, tiende a estabilizarse en cero, el punto de equilibrio es un atractor (estable según Lyapunov) ya que f'(x0) < 0.

* Sí t −→ ∞⁻ la concentración restante de desechos e impurezas se aleja del punto de equilibrio haciendo que el punto de equilibrio sea repulsor. [6]

4. Modelamiento usando sistema de ecuaciones lineales diferenciales.

* Sea x(t) la concentración de impurezas en la sangre a lo largo de la membrana en el tiempo t.

* Sea y(t) la concentración de impurezas en el líquido de diálisis. El líquido de la diálisis es el que purifica la sangre y cuando pasa por el hemodializador esta se purifica.

* a ∈ R⁺ la constante que mide la eficacia del líquido de diálisis.

* v y V las tasas de flujo volumétrico de la sangre y del líquido de diálisis, respectivamente.[8]

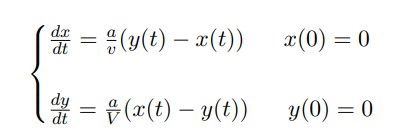
4.1 Cálculo de los valores propios del Sistema de ecuaciones.

Distribuimos la constante a/v y a/V en el sistema de ecuaciones

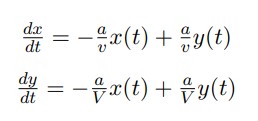
Ahora procedemos a sacar los valores propios de la matriz

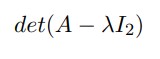
Reemplazamos

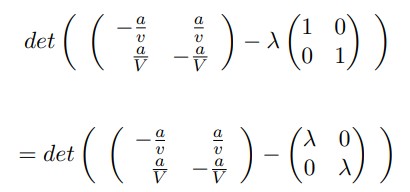
Restamos las dos matrices

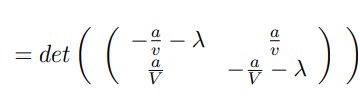
Ahora sacamos el determinante de la matriz dada:

Distribuimos

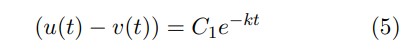
Y, en consecuencia, obtenemos el polinomio característico:

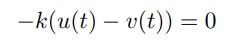
Donde T = (− a/v − a/V) y D = (a (a/vV − 1/V + 1/v)) Del polinomio característico obtenemos los valores propios λ1 = 0 y λ2 = − a/v − a/V que, por el teorema de Lyapunov, son asintóticamente estables

Tomamos la consideración para cuando el valor propio λ1 = 0

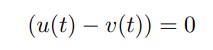
Reemplazamos

De la anterior expresión se obtiene el siguiente Sistema Lineal

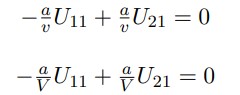
Solucionando el sistema anterior se hallan los valores U₁₁, U₂₁

Entonces,

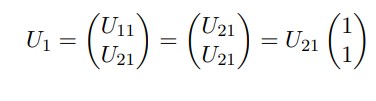
observese los puntos de la forma k₁(¹ ₁)

Para cualquier k₁, son puntos de equilibrio para este sistema. En efecto,

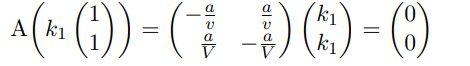
Por consiguiente, todo aquel punto que este sobre la línea recta de vectores propios asociados a λ1 = 0 es un punto de equilibrio

Ahora tomamos la consideración para cuando λ2 = − a/v − a/V

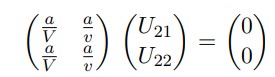
De la anterior expresión se obtiene el siguiente sistema lineal

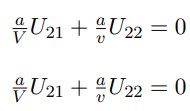
Solucionando el sistema anterior se hallan los valores de U₂₁, U₂₂

Entonces,

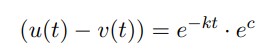
En este sistema de ecuaciones la ecuación general es:

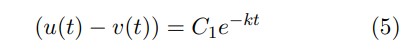
Vemos que la solución general depende de t solamente a través del segundo sumando. Si se hace k2 = 0, X(t) = k1 (¹ ₁) el cual no depende del tiempo En este caso, todos los puntos k1 (¹ ₁) para cualquier k1, son puntos de equilibrio es decir el sistema tiende a estabilizarse

Como λ2 < 0 el segundo sumando tiende a estabilizarse cuando han transcurrido las 4 horas, por consiguiente la solución

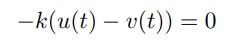
tiende al punto de equilibrio k1 (¹ ₁) a lo largo de una paralela a l₂

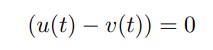
5. ¿Qué es la tasa de flujo volumétrico?

El término tasa de flujo volumétrico Q de un fluido como el volumen de fluido que pasa a través de una sección transversal dada por unidad de tiempo. El término sección transversal es solo una forma de describir el área a través de la que algo fluye, por ejemplo, el área circular dentro de la recta punteada en el diagrama que se muestra a continuación. [2]

Como la tasa de flujo volumétrico mide la cantidad de volumen que pasa a través de un área en un tiempo dado, su ecuación se ve así:

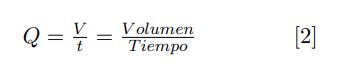
5.1 Calculando los parámetros:

Las tasas de flujo volumétrico de la sangre y del líquido de diálisis, respectivamente se calculan de la siguiente manera:

Datos:

• 161,5 litros de sangre que es la cantidad de sangre que circula en el riñón.

• 24h es el tiempo que circula la sangre en el riñón

Nota: Se debe tener en cuenta que 161,5 litros desangre que circula en el riñón es la de un paciente con insuficiencia renal.

Ahora realizaremos el cálculo del líquido de la diálisis:

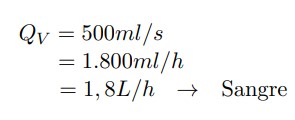
6. Usando las condiciones iniciales:

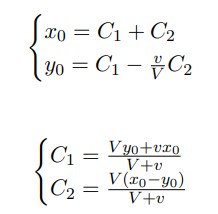
Por último, obtenemos el campo de direcciones y la gráfica del comportamiento de las soluciones.

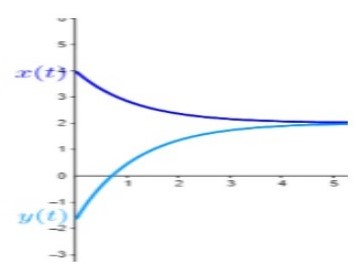
Figura.1. Curvas solución.

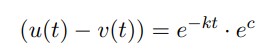
Figura 2. Campo de direcciones.

Conclusiones:

Este modelo nos permite analizar el comportamiento del procedimiento de la diálisis de un paciente con insuficiencia real.

Se realizó el respectivo an´alisis cualitativo de los dos modelos que se emplean para un riñón artificial, en donde en el primer modelo (que está dado por una ecuación diferencial) se analizó cuándo, en un determinado tiempo, la diferencia de la concentración de desechos e impurezas se estabiliza, es decir, en dónde la concentración de desechos desaparece, quedando la sangre limpia

En el segundo modelo (que está dado por un sistema de ecuaciones) se realizó el respectivo análisis cualitativo, y se calcularon los parámetros en se tuvo en cuenta que la sangre que circula en el riñón de una persona con insuficiencia renal no es la misma cantidad que circula en un paciente sano.

Se analizó en el segundo modelo que transcurridas las 4 horas del proceso de dializado, y la concentración de impurezas de la sangre y del líquido de la diálisis tiende a estabilizarse.

Bibliografía:

[1]      Suhail Ahmad, MD Professor, Medicine University of Washington Scribner Kidney Center Northwest Kidney Centers Seattle, Washington.sahmad@u.washington.edu. Seattle, Washington, USA July 1999 ‘Manual of Clinical Dialysis, Second Edition’.

[2]      Nave, R. ”Bulk Elastic Properties (Propiedades elásticas de los medios continuos).” HyperPhysics (artículo en inglés). http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html.https://es.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is volume-flow-rate

[3]      Mariusz Zio’Iko, Jacek a. Pietrzyk, and Joanna Grabska-Chrza. Stowska. Kidney International, Vol. 57 (2000), pp. 1152–1163. Accuracy of hemodialysis modeling.

[4]      Vanessa Fernández Martínez, Laura Pérez Valencia, Javier Fernández- Caro Sánchez, María Ruíz Serna, Julia Madrid Garrido, Virginia Caparrós Ros, Francisca García Navarro, María Victoria Vilar Torres. Influencia en la dosis de diálisis de diferentes flujos de líquido dializante en el paciente tratado con hemodiafiltración on-line o hemodiálisis convencional. Obtenido de: http://www.revistaseden.org/files/2739_26%20%201565.pdf

[5]      Luis Arturo Polania Quizá Periodo 2018-1 de 2010. Un enfoque cualitativo a las EDO’S y teoría Wavelets.

[6]      Miguel de Córdoba. (5 de agosto de 2010). Lo esencial de la circulación. Obtenido de Fisiologoi: https://fisiologoi.com/paginas/flujo/circulacion.htm

[7]      Universidad de las Palmas de Gran Canaria (2003) - Fluidos ideales. Obtenido de https://www2.ulpgc.es/descargadirecta.php?codigo_archivo=5211

[8]      Modelos matemáticos en Biología. Teoría. Universidad de JAEN. Departamento de Matemáticas. 2009