Enero-Diciembre 2020;5(1)
Resonancia Fano en un cristal fotónico unidimensional superconductor
Fano resonance in a superconducting one-dimensional photonic crystal
Mariana Salcedo-Camacho1
Francis Segovia2
Resumen
En este artículo, estudiamos el comportamiento de la resonancia Fano en un cristal fotónico unidimensional (CF-1D) compuesto por capas alternas de Nibio (Nb) y Bismuto Estroncio Calcio Oxido de Cobre (BSCCO), materiales superconductores, junto con una capa de material dieléctrico como defecto al final de la estructura. Se utilizó el método de la matriz de transferencia para calcular el espectro de reflectancia para la polarización transversal eléctrica (TE) del CF-1D Superconductor al ser sometido a variaciones de parámetros como: el ángulo de incidencia de la onda electromagnética, el número de periodos, el índice de refracción del dieléctrico, el espesor de la capa superconductora y la temperatura.
En los resultados se observan dos modos resonantes, uno perteneciente a la resonancia Fano y otro a la reflectancia electromagnética inducida (REI); los cuales, al aumentar el ángulo de incidencia y la temperatura, presentan un corrimiento a longitudes de onda cortas; al aumentar el número de periodos, un crecimiento de los picos reflectantes; al aumentar el índice de refracción de la capa dieléctrica, cambio del modo resonante REI a resonancia Fano; al aumentar el espesor de la capa compuesta por Nb, aumento en el número de modos resonantes con corrimiento a longitudes de onda largas. Este estudio muestra la dependencia de las propiedades de la resonancia Fano cono los diferentes parámetros usados, demostrando su utilidad en la comprensión del espectro resonante obtenido y su aplicabilidad en filtros ópticos, dispositivos de conmutación óptica y otros dispositivos fotónicos.
Palabras clave:: Cristal fotónico, Método de la Matriz de Transferencia, Superconductor, Reflectancia, Resonancia Fano, Reflectancia Electromagnética Inducida.
Abstract
In this article, we studied the behavior of Fano resonance in a one-dimensional photonic crystal (1D-PC) composed of alternating layers of Nibium (Nb) and Bismuth Strontium Calcium Copper Oxide (BSCCO), superconducting materials, with a layer of dielectric material as defect at the end of the structure. The transfer matrix method was used to calculate the reflectance spectrum for Superconductor 1D-PC with electrical transverse polarization (TE) when subjected to variations in parameters such as: the incidence angle of the electromagnetic wave, the periods number, the refractive index of the dielectric, the thickness of the superconducting layer and the temperature.
In the results two resonant modes are observed, one belonging to the Fano resonance and the other to the induced electromagnetic reflectance (EIR); which, when increasing the incidence angle and the temperature, present a change to short wavelengths; To the increases the period number, a growth in reflective peaks; as the refractive index of the dielectric layer increases, change the form of EIR mode to Fano resonance; as the thickness of the Nb layer increases, the number of resonant modes increases too, with a change to long wavelengths. This study shows the dependence of the Fano resonance properties with different parameters used, demonstrating its usefulness in understanding the resonant spectrum obtained and its applicability in optical filters, optical switching devices and other photonic devices.
As a result, it was evident that the hotel sector of the municipality of San Agustín Huila does not have a documented personnel selection process, and they also lack a dependency for this process, since it is carried out by the same administrator or owner. Within the requirements that hotels request when hiring staff, they do not require applicants to have higher academic studies, although some of them do request a certain command of English and part of the experience for higher positions on the part of the candidate, taking into account that the municipality of San Agust´ın is a tourist destination.
Keywords:: Photonic crystal, Transfer matrix method, Superconductor, Reflectance, Fano resonance, Induced Electromagnetic Reflectance.
Introducción
Los cristales fotónicos (CF), nanoestructuras artificiales constituidas por capas alternas de distinta constante dieléctrica organizadas de forma periódica (Joannopulos 2008), fueron definidos por primera vez de manera simultánea por E. Yablonovitch, al estudiar la eficiencia de los láseres evitando las pérdidas de energía debido a la emisión espontánea (Yablonovitch 1987) y S. John, en la búsqueda de un medio en el que se pudiera confinar la luz (Sajeev 1987). Se caracterizan por presentar regiones de frecuencia especificadas en las cuales las ondas electromagnéticas no pueden propagarse o transmitirse, consecuencia del contraste entre los índices de refracción que componen la estructura, llamadas brechas de banda fotónicas (BBFs) prohibidas, las cuales los define como parte fundamental en el control del flujo de la radiación electromagnética puesto que, al adicionar en la estructura un defecto que rompa su periodicidad espacial, generan regiones conductoras dentro de las BBFs permitiendo el flujo de la luz, llamados modos de defecto localizados (Brechet, Marcou, Pagnoux y Roy 2000; Barkat 2015). Las direcciones en las cuales se puede propagar la onda electromagnética dependen de la periodicidad espacial del CF, existiendo entonces 3 tipos de CFs: unidimensionales (1D), bidimensionales (2D) y tridimensionales (3D) (Zi, Wan y Zhang 1998).
Los avances de la física en el ajuste de las propiedades ópticas de los cristales fotónicos, ha propuesto usar diversos tipos de materiales en la construcción de estas estructuras, tales como semiconductores (Sánchez y Porras 2016), metales (Gharaali y Zare 2017), superconductores (Zamani 2016; Wu y Gao 2015), metamateriales (Barati y Aghajamali 2016), cristales líquidos, entre otros ( González, Ordoñes, Zambrano y Porras 2017). Los superconductores son los materiales con mayor atención en el estudio de la nano foónica ya que presentan resistencia cero (Qiao 1995); es decir, menor pérdida de las ondas electromagnéticas, aún por debajo de su temperatura crítica (Tc) (Rainer 1998), característica que permite la sintonización de las BBF al ser usados en CFs, debido a la dependencia de sus propiedades ópticas con parámetros como el ángulo de incidencia de la onda electromagnética (Hu, Liu, Wu, Yang y Yang 2013), el grosor de las capas que componen la estructura cristalina (Segovia y Vinck 2018), la temperatura y la presión hidrostática (Herrera, Calero y Porras 2018), como consecuencia de la relación entre el campo eléctrico y el campo magnético con su constante dieléctrica (Wu, Liao y Chang 2010). Los CFs-1D compuestos por materiales superconductores, son útiles aplicaciones como: detección térmica (Upadhyay, Awasthi, Shiveshwari, Srivastava y Ojha 2015), reflectores y filtros de paso de banda (Aly y Mohamed 2015), dispositivos operativos para espectros de transmisión de banda plana y ancha (Zamani 2015), sensores de baja temperatura (Wu y Gao 2015), etc.
U. Fano, presentó una descripción teórica completa para el análisis de formas de líneas asimétricas, también llamadas resonancia Fano (Fano 1961); fue observada por primera vez en estructuras plasmónicas (Rahmani, Lukyanchuk y Hong 2012) y es fundamental en la descripción de fenómenos resonantes en una amplia gama de sistemas, puesto que permite determinar el origen de las formas de línea asimétricas en términos de fenómenos de interferencia constructivos y destructivos en el espectro de reflectancia (Zhou, Zhao, Shuai, Yang, Chuwongin, Chadha y Fan 2014), dando a conocer el punto exacto de los dos puntos críticos que la caracterizan: el desvanecimiento de la eficiencia dispersiva y la toma del valor máximo cerca a la unidad, indicando el momento exacto en que el espectro e dispersión cambia de reflexión total a transmisión total (Limonov, Rybin, Poddubny y Kivshar 2017). La resonancia Fano es aplicada controlar el transporte y las propiedades de dispersión de las ondas electromagnéticas en dispositivos electrónicos a nano escala (Miroshnichenko, Flach y Kivshar 2010).
Teniendo en cuenta las propiedades ópticas descritas anteriormente, en este trabajo se propone un CF-1D compuesto por capas alternas de Nibio (Nb) y Bismuto Estroncio Calcio Oxido de Cobre (BSCCO), materiales superconductores, junto con una capa de material dieléctrico como defecto al final de la estructura, calculando el espectro de transmitancia a través del método de la matriz de transferencia con el fin de estudiar los efectos de parámetros como: el ángulo de incidencia de la onda electromagnética, la temperatura, el número de periodos, el índice de refracción de la capa dieléctrica y el espesor de la capa superconductora sobre la resonancia Fano. Con esta investigación, se pretende contribuir teóricamente en futuras experimentaciones de CFs y dise˜nos de dispositivos fotónicos.
Metodología:
La figura 1 muestra el diagrama de un CF-1D superconductor finito, inmerso en aire, con periodicidad N a lo largo del eje x; compuesto por Nibio (Nb) (capa A) y Bismuto Estroncio Calcio Oxido de Cobre (BSCCO) (capa B), materiales superconductores mostrados en la Figura 1a; con la adición de un material dieléctrico como defecto al final de la estructura (Capa C) observado en la figura 1b. Los índices de refracción de los medios son: nA y nB respectivamente y son determinados por la raíz cuadrada de la permeabilidad relativa para los materiales superconductores, dada por:
εs(ω) = 1 − c2 / ω2λ2L (1)
Donde c es la velocidad de la luz en el vacío y λL la longitud de penetración London definida por:
λL(T) = λ0 / √1 − (T / Tc)q (2)
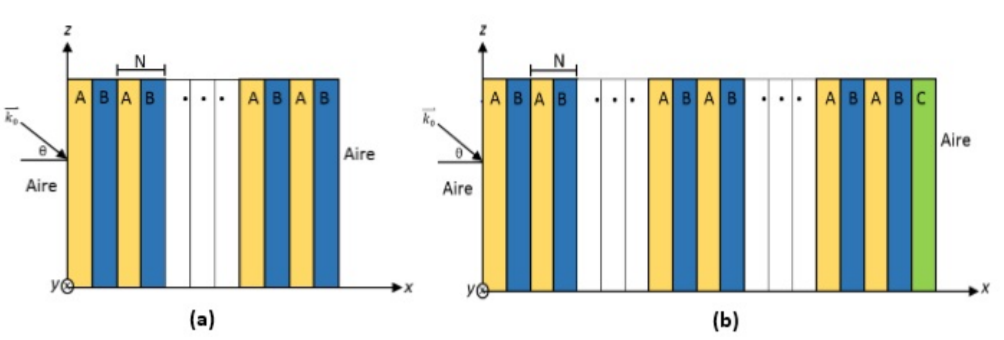
Figura 1. Estructura del CF-1D Superconductor inmerso en aire, (a) compuesto por dos materiales superconductores diferentes A y B, sin la adición de la capa defectuosa (b) con la adición de la capa dieléctrica C como defecto.
siendo λ0 la longitud de penetración a T=0K, T la temperatura que opera sobre la estructura cristalina, Tc la temperatura crítica característica de cada material superconductor y q un parámetro dependiente del superconductor de manera que, para materiales con Tc altas (BSCCO) q=2 y para Tc bajas (Nb) q=4.
El estudio de la interacción entre las ondas electromagnéticas en un CF es posible gracias al modelo matemático publicado por J. Maxwell en 1865 compuesto por cuatro leyes fundamentales llamadas las “ecuaciones de Maxwell”. Considerando para el estudio de la luz dentro de la nanoestructura cristalina propuesta el modo transversal eléctrico (TE) y, teniendo en cuenta que el método de la matriz de transferencia permite estudiar la interacción del campo eléctrico dentro del CF-1D superconductor a lo largo de una dirección especificada a través de matrices dinámicas y de propagación, se tiene entonces, la representación de cada capa de la forma:
Mj = DjPjDj−1 con j = A, B, C, . (3)
Con una matriz de propagación Pj definida de la siguiente manera:
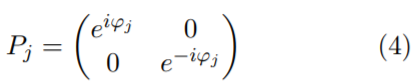
Y la fase ϕj expresada como:
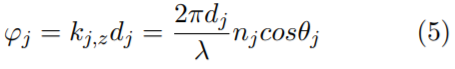
Donde los parámetros dj , nj y θj representan en la capa j-ésima el espesor, el índice de refracción y el ángulo de incidencia, respectivamente.
La matriz dinámica para ondas TE está dada por:
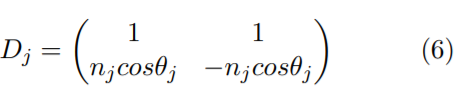
Teniendo finalmente la matriz de transferencia total para la estructura del CF-1D superconductor (Aire-(AB) N - Aire) dada por:
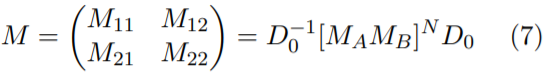
con D0 representando la matriz dinámica del aire y, determinando para el caso de incidencia normal el coeficiente de reflexión r a partir de:

Siendo M11 y M21 los elementos matriciales de la matriz de transferencia total (ecuación 7). Por último, la reflectancia para una onda electromagnética incidente es definida por:

En este caso, la matriz de transferencia total, con la capa defectuosa C, está dada por:
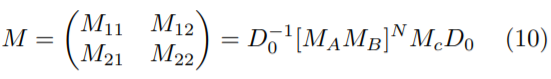
Resultados:
En esta sección, presentamos los resultados teóricos obtenidos al calcular el espectro de reflectancia del CF-1D superconductor para polarización TE. Los valores usados en los parámetros que caracterizan la estructura cristalina para realizar la simulación son los siguientes: para la primera capa compuesta por Nb, un espesor dA=0.07µm, una temperatura crítica TcA=9.25K , con una longitud de penetración λ0A=0.0834µm; para la segunda capa compuesta por BSCCO, un dB=0.01µm, una TcB=95K y una λ0B=0.15µm. Como temperatura operacional sobre el cristal fotónico, se propone una T=4.2K y para el número de periodos un N=50.
En la figura 2a, se muestra la gráfica de reflectancia en función de la longitud de onda para el cristal fotónico propuesto, inmerso en aire, bajo las condiciones iniciales expuestas anteriormente; mientras que la figura 2b, ilustra el espectro reflectante al adicionar la capa defectuosa C, compuesta por un material dieléctrico con espesor dC=0.02µm e índice de refracción nC=2.5, aún bajo las condiciones iniciales.
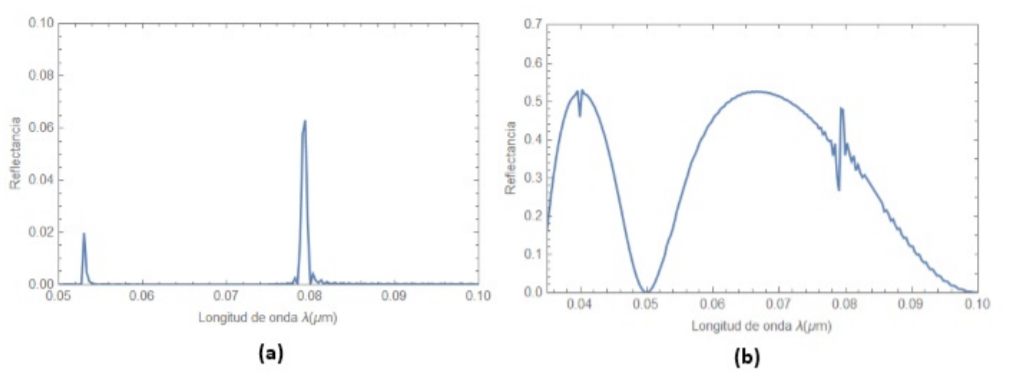
Figura 2. Espectro de reflectancia de nuestro CF-1D superconductor sin defecto (a) y con defecto (b) en función de la longitud de onda para un ángulo de incidencia normal.
A continuación, comenzamos a mostrar los diferentes efectos que presenta el espectro de resonancia de nuestro CF-1D Superconductor, al variar diferentes parámetros sobre nuestra estructura cristalina. La figura 3, ilustra la reflectancia en función de la longitud de onda, al variar el ángulo de incidencia de la onda electromagnética con valores: = 0° (azul), = 10° (roja), = 20° (negra) y = 30° (verde).
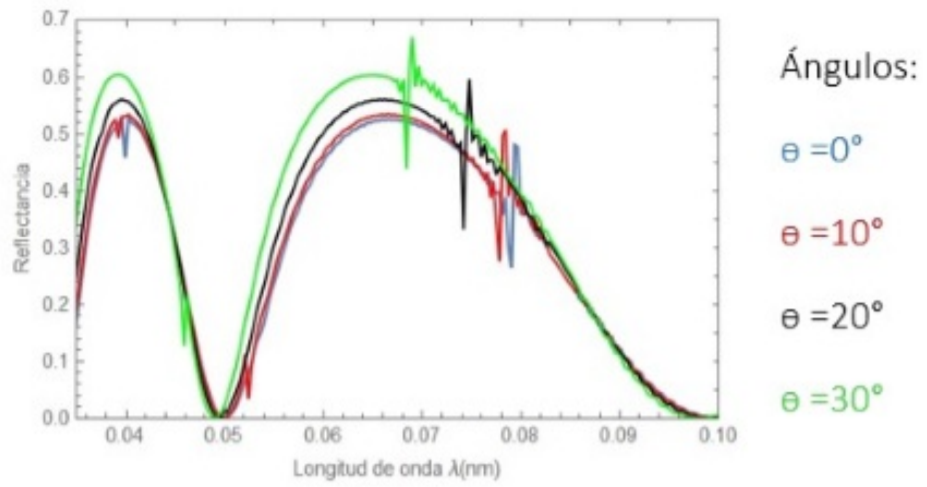
Figura 3. Espectro de reflectancia de nuestro CF-1D superconductor con variación del ángulo de incidencia Ɵ de la onda electromagnética
Los efectos sobre el espectro de reflectancia al variar el número de periodos de la estructura cristalina son presentados en la figura 4, la variación de este parámetro se realiza para los valores: N=30 (azul), N=50 (roja), N=70 (negra) y N=90 (verde).
Los cambios en el espectro de reflectancia al variar el ángulo de incidencia de la capa defectuosa compuesta por un material dieléctrico ubicada al final de la estructura cristalina son especificados en la figura 5, para valores: nC=1.3µm (azul), nC=1.6µm (rojo), nC=2.0µm (negro) y nC=2.5µm (verde).
En la siguiente gráfica, la figura 6, se observan las curvas que caracterizan el espectro de reflectancia al someter el CF-1D a una variación en el espesor de su primera capa superconductora A compuesta por Nb.
Finalmente, la figura 7, muestra el comportamiento del espectro de reflectancia al presentar cambios la temperatura que opera sobre el CF-1D superconductor con valores: T=2K (azul), T=4K (rojo), T=6K (negro) y T=7K (verde).
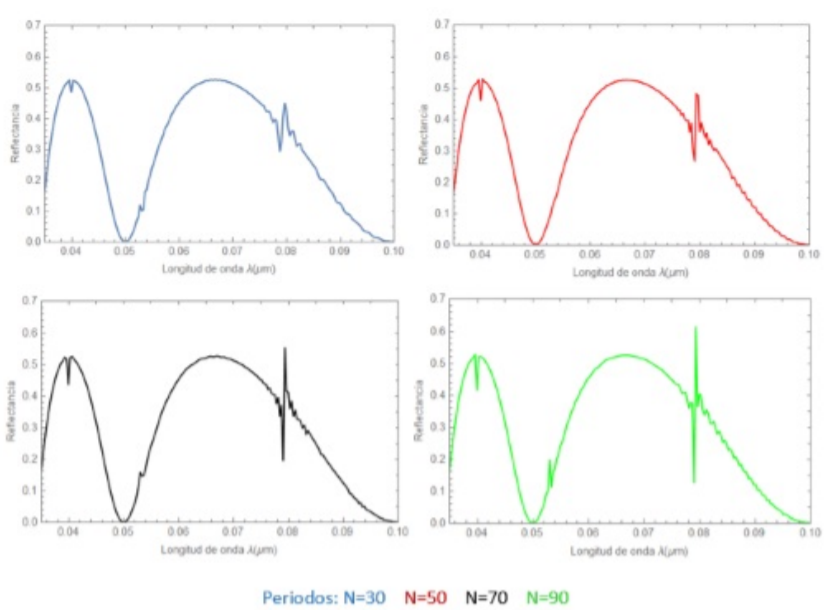
Figura 4. Espectro de reflectancia con variación del número de periodos N de nuestro CF-1D superconductor

Figura 5. Espectro de reflectancia con variación del índice de refracción de la capa defectuosa nC en el CF-1D superconductor
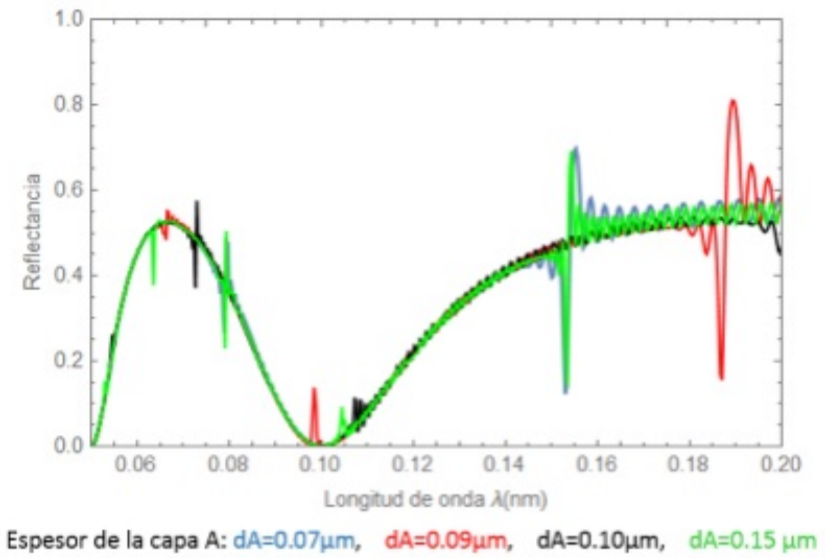
Figura 6. Espectro de reflectancia para diferentes espesores de la capa A superconductora en el CF-1D
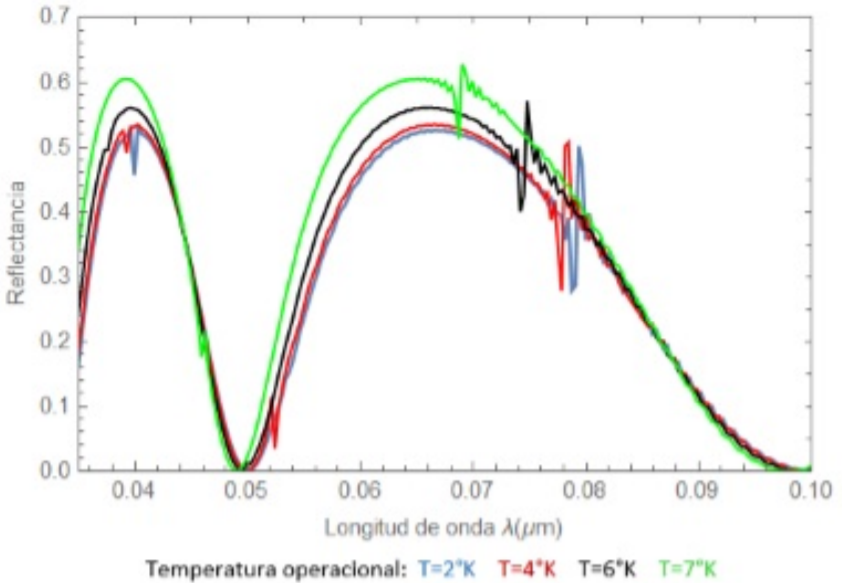
Figura 7. Variación del espectro de reflectancia para diferentes valores de temperatura operacional sobre el CF-1D Superconductor.
Discusión:
En la figura 2, se observa el espectro de reflectancia con un ángulo de incidencia normal, para el CF-1D Superconductor propuesto inmerso en aire, sometido a parámetros bajo las condiciones iniciales descritas anteriormente; se observa en la figura 2a, correspondiente a la nanoestructura fotónica en ausencia de la capa defectuosa, dos picos resonantes simétricos, el primero con reflectancia igual a 0.02, en un rango de longitud de onda de (0.052-0.054)nm y el segundo con una altura aproximada de 0.062 en un rango de λ entre los 0.078 y 0.080 nanómetros. Por otra parte, la figura 2b, representa las características de la reflectancia al añadir una capa defectuosa C al final de la estructura; se observan 2 fenómenos resonantes diferentes, uno con forma de línea simétrica identificado como reflectancia electromagnética inducida (REI) en longitudes de onda alrededor de los 0.04nm y el otro con forma de línea asimétrica, referente a la resonancia Fano con valores de longitud de onda próximos al rango entre los 0.078-0.080 nanómetros.
Los efectos de la variación del ángulo de incidencia de la onda electromagnética sobre el espectro de reflectancia son mostrados en la figura 3, presentando grandes cambios en las características de la resonancia Fano y la REI, puesto que al aumentar este parámetro existe corrimiento de los fenámenos resonantes a longitudes de onda cortas y, al llegar a valores de θ iguales a 30 y 40 grados un cambio en el primer pico resonante a una forma de línea asimétrica.
El número de periodos, representa un papel importante en los fenómenos resonantes presentes en el espectro de reflectancia enseñado en la figura 4, ya que el aumento de este parámetro disminuye el rango en que se presenta la resonancia Fano, pasando de un rango de longitud de onda para N=30 entre 0.078-0.081 nm a uno entre 0.078-0.080 nm cuando N=90; así como también el aumento de los picos reflectantes, pasando de 0.320 y 0.460 a 0.140 y 0.620 para el menor y el mayor número de periodos respectivamente. El pico reflectante de REI disminuye, cambiando de 0.480 a 0.415.
La figura 5, ilustra cambios en las características de los fenómenos resonantes presentados en el espectro de reflectancia al variar el índice de refracción de la capa defectuosa C, compuesta por un material dieléctrico; observando, para un valor de nC=1.3µm unas formas de línea: asimétrica con valores en la reflectancia entre 0.00-0.10 y simétrica con un pico reflectante de 0.40 las cuales, presentan cambios a medida que se aumenta el índice de refracción, la primera forma de línea asimétrica llegando a un punto máximo y mínimo en la reflectancia de 0.54 y 0.28 respectivamente; mientras que la otra, pasó de simétrica a una forma asimétrica cuando nC=2.5µm con 0.70 y 0.20 como puntos máximos y mínimos.
Existen diversos cambios importantes en el comportamiento de los fenómenos resonantes expuestos en la figura 6 al variar el espesor de la capa superconductora A compuesta por Nb. La resonancia Fano y REI, presentan corrimiento a longitudes de onda largas, los picos reflectantes máximos-mínimos sufren crecimientos a puntos altos y bajos respectivamente y, se observan nuevos modos resonantes simétricos y asimétricos a medida que se aumenta el espesor de A.
Finalmente, los efectos de la Temperatura operacional sobre el CF-1D Superconductor son presentados en la figura 7, observando un corrimiento de la resonancia Fano y REI a longitudes de onda cortas, así como también cambios en los máximos y mínimos de los fenómenos, específicamente para la resonancia Fano, que pasa de 0.28 y 0.5 a 0.52 y 0.62 respectivamente.
De acuerdo a los resultados descritos y estudiados anteriormente, se identifican las características pertenecientes a la resonancia Fano en cada una de las figuras obtenidas, permitiendo comprender las diversas aplicaciones que el estudio de este fenómeno representa en las investigaciones de los cristales fotónicos unidimensionales superconductores. El observar la resonancia Fano al adicionar la capa C como defecto al final de la nanoestructura en la figura 2b, muestra que es posible el cambio en el espectro de reflectancia de un punto de reflexión total a uno de transmisión total; por otra parte, los cambios de la forma de línea simétrica a una forma asimétrica presentes en la figura 5, permiten observar los fenómenos de interferencia constructivos y destructivos experimentados por las ondas electromagnéticas dentro del cristal; Finalmente, la influencia del número de periodos sobre el comportamiento de la resonancia Fano en la figura 7, demuestra el papel fundamental que representa este parámetro en el ajuste de las características de este fenómeno.
El estudio del comportamiento de la resonancia Fano en el CF-1D Superconductor propuesto en este trabajo, proporciona a la comunidad científica datos teóricos útiles en la fabricación de nuevos dispositivos de conmutación óptica, interruptores, sensores, láseres, entre otros instrumentos ópticos
Agradecimientos:
Estamos agradecidos por la financiación de este proyecto de investigación por parte de la Vicerrector´ıa de investigación de la Universidad Surcolombiana, Neiva-Huila.
Referencias:
Aly A., Mohamed D. (2015), BSCCO/SrTiO3 one dimensional superconducting photonic crystal for many applications, J. Supercond. Nov. Magn. 28.
Barati M., Aghajamali A. (2016), Near-infrared tunable narrow filter properties in a 1D photonic crystal containing semiconductor metamaterial photonic quantum-well defect. Physica E 79.
Barkat O. (2015), Theoretical investigation of transmission and disperssion properties of one dimensional Photonic crystals, Journal of Electrical and Electronic Engineering, Vol.3, No 2, pp. 12-18.
Brechet F., Marcou J., Pagnoux D., Roy P. (2000), Complete analysis of the characteristics of propagation into photonic crystal fibers, by the finite element method, Optical Fiber Technology, Vol. 6,pp. 181-191.
Gharaali A., Zare Z. (2017), The effect of temperature on onedimensional nanometallic photonic crystals with coupled defects, Pramana-J. Phys. 88.
Gonzalez L., Ordonez J., Zambrano G., Porras N. (2017), YBa2Cu3O7-x/BaTiO3 1D Superconducting Photonic Crystal with Tunable Broadband Response in the Visible Range, CrossMark.
Herrera A., Calero J., Porras-Montenegro N. (2018), Pressure, temperature, and thickness dependence of transmittance in a 1D superconductor-semiconductor photonic crystal, J. Appl. Phys. 123.
Hu C., Liu J., Wu C., Yang T., Yang S. (2013), Effects of superconducting film on the defect mode in dielectric photonic crystal heterostructure, Sol. State Commun.
Joannopoulos J. (2008), Photonic Crystals, Molding the flow of light, Princeton University Press, New Jersey
Limonov M., Rybin M., Poddubny A., Kivshar Y. (2017), Fano resonances in photonics. Nature Photonics, 11(9).
Miroshnichenko A., Flach S., Kivshar Y. (2010), Fano resonances in nanoscale structures. Reviews of Modern Physics.
Qiao J. (1995), High-Tc superconductors on buffered silicon: materials properties and device applications, Materials Science and Engineering: R: Reports, 14(4).
Rahmani M., Lukyanchuk B., Hong M. (2012), Fano resonance in novel plasmonic nanostructures. Laser & Photonics Reviews.
Rainer W. (1998), High-Temperature Superconductors: Materials, Properties, and Applications, kluwer academic publishers, New York.
Sajeev J. (1987), Strong localization of photons in certain disordered dielectric superlattices, Physical Review Letters.
Sanchez-Cano R., Porras-Montenegro N. (2016), Temperature dependence of band gap ratio and Q-factor defect mode in a semiconductor quaternary alloy hexagonal photonic crystal hole slab. Appl. Phys. A 122.
Sarrazin M., Vigneron J., Vigoureux J. (2003), Role of Wood anomalies in optical properties of thin metallic films with a bidimensional array of subwavelength holes, Phys. Rev. B 67.
Segovia-Chaves F., Vinck-Posada H. (2018), Tuning of transmittance spectrum in a one-dimensional superconductor-semiconductor photonic crystal, Physica B: Condensed Matter.
Upadhyay M., Awasthi S., Shiveshwari L., Srivastava P., Ojha S. (2015), Thermally tunable photonic filter for WDM networks using 1D superconductor dielectric photonic crystals, J. Supercond. Nov. Magn. 28.
Wu C., Liao J., Chang T. (2010), Tunable multilayer Fabry–Perot resonator using electro-optical defect layer, J. Electromagn. Waves Appl. 24.
Wu J., Gao J. (2015), Analysis of temperature-dependent optical properties in 1D ternary superconducting photonic crystal with mirror symmetry. J. Supercond. Nov. Magn. 28.
Wu J., Gao J. (2015), Low temperature sensor based on onedimensional photonic crystals with a dielectric-superconducting pair defect, Optik 126.
Yablonovitch E. (1987), Inhibited spontaneousemission in solid-state physics and electronics, Physical Review Letters, Vol.58.
Zamani M. (2015), All superconducting photonic crystals with wideband flat-top responses in visible region. J. Supercond. Nov. Magn. 28.
Zamani M. (2016), Spectral properties of all superconducting photonic crystals comprising pair of high-high, low-low or high-low temperature superconductors, Physica C: Super. Appl. 520.
Zhou W., Zhao D., Shuai Y., Yang H., Chuwongin S., Chadha A., Fan S. (2014), Progress in 2D photonic crystal Fano resonance photonics. Progress in Quantum Electronics.
Zi J., Wan J., Zhang C. (1998), Large frecuency range of negligible transmission in one-dimensional photonic quantum well structures, Applied Physics Letter, Vol.73, No15.
1 Estudiante Semillero de Física Matemática; Programa de Física-Universidad Surcolombiana Neiva-Huila
2 Profesor Programa de Física-Universidad Surcolombiana Neiva-Huila