
Revista Erasmus Volumen 6
Enero-Diciembre 2021;
Estudio del flujo de energía en un cristal fotónico unidimensional aperiódico compuesto por materiales polímeros
Study of the energy flow in a one-dimensional aperiodic photonic crystal composed of polymer materials
Valentina Avilés León
Estudiante semillero de Física matemática
Programa de Física
u20151135692@usco.edu.co
Lina Rocio Lorena Barbosa Gómez
Estudiante semillero de Física matemática
Programa de Física
u20161147367@usco.edu.co
Francis Segovia-Chaves
Grupo de Física Teórica
Programa de Física-Universidad Surcolombiana
francis.segovia@usco.edu.co
Resumen
En este trabajo se determinó el comportamiento de la radiación electromagnética para un cuasicristal fotónico unidimensional organizado por una sucesión de Fibonacci con polarización TE (Transversal Eléctrica) y TM (Transversal Magnética) para diferentes ángulos de incidencia. Un cristal fotónico se clasifica como cuasiperiódico cuando posee una estructura ordenada y una aperiócidad en su índice de refracción. Sus capas se alternan siguiendo una regla recursiva de Fibonacci para materiales polímeros: PS (poliestireno) y PMMA (polimetacrilato de metilo). El comportamiento de la radiación se registra a través de un espectro de transmitancia calculado por el MMT (Método de la Matriz de Transferencia). Se evidencio la presencia de BBFs (Brechas de Banda Fotónica) las cuales, se controlaron variando parámetros como: la secuencia de Fibonacci, el ángulo de incidencia de la luz y el grosor de las capas de los materiales. Se encontró que al aumentar el ángulo de incidencia de la onda electromagnética sobre el cuasicristal observamos un corrimiento de la BBF (Brechas de Banda Fotónica) hacia frecuencias altas. Además, se comprueba que al incrementar la secuencia de Fibonacci el número de gaps presentes en el espectro de transmisión aumenta, al igual que el número de capas en la estructura. Por otra parte, se demostró que la polarización TM (Transversal Magnética) presenta un mayor número de gaps con valores menores en la transmitancia. Finalmente, al aumentar el grosor de las capas de los materiales, con presión y secuencia constante las BBFs (Brechas de Banda Fotónica) muestran un corrimiento hacia frecuencias bajas para ambas polarizaciones (TE y TM).
Abstract
In this work, the behavior of electromagnetic radiation was determined for a one-dimensional photonic quasi-crystal organized by a succession of Fibonacci with TE (Transverse Electric) and TM (Transverse Magnetic) polarization for different angles of incidence. A photonic crystal is classified as quasi-periodic when it has an ordered structure and an aperiosity in its refractive index. Its’ layers alternate following a Fibonacci recursive rule for polymer materials: PS (Polystyrene) and PMMA (Polymethyl methacrylate). The radiation behavior is recorded through a transmittance spectrum calculated by the TMM (Transfer Matrix Method). The presence of PBGs (Photonic Band Gaps) was evidenced, which were controlled by varying parameters such as The Fibonacci sequence, the light incidence angle, and the thickness of the material layers. It was found that by increasing the angle of incidence of the electromagnetic wave on the quasi-crystal we observed a shift of the PBGs (Photonic Band Gaps) toward high frequencies. In addition, it was found that by increasing the Fibonacci sequence the number of gaps present in the transmission spectrum increases, as does the number of layers in the structure. On the other hand, it was shown that the TM (Transverse Magnetic) polarization presents a greater number of gaps with lower values in the transmittance. Finally, as the thickness of the layers of the materials increase with constant pressure and sequence the PBGs (Photonic Band Gaps) show a shift toward low frequencies for both polarizations (TE and TM).
Keywords:
Energy flow, quasi-crystal, Fibonacci sequence, transfer matrix method (TMM).
Introducción
Los primeros estudios en cristales fotónicos (CFs) fueron desarrollados por Lord Rayleigh en 1887 al explicar el comportamiento de una onda electromagnética que se refleja en la interface de dos medios con diferente constante dieléctrica (Elmore y Heald, 1985). Expuso que los cristales con periodicidad y con distinta constante dieléctrica son buenos reflectores de luz (Meade, Winn y Joannopoulos, 1995). Eli Yablonovitch, en su artículo publicado en 1987, sustenta que la emisión espontánea de los átomos no es un efecto fijo y que el acoplamiento entre materia y espacio puede ser controlado por las propiedades del campo de radiación (Yablonovitch, 1987). El descubrimiento de los cuasicristales por Dan Shechtman en 1984, dio un gran comienzo al mundo de las estructuras aperiódicas (Dal Negro, 2013).
Un cristal fotónico se define como una estructura ordenada (Yariv y Yeh, 1984) que presenta una periodicidad espacial de la constante dieléctrica (Segovia-Chaves y Vinck-Posada, 2018). La periócidad en el índice de refracción provoca que las interferencias de ondas planas sean constructivas o destructivas para ciertas direcciones y para ciertos rangos de energía (Abirami y Wilson, 2019), ocasionando bandas permitidas o Brechas de Bandas Fotónicas (BBFs) (Saleh y Teich, 2019). Una BBF es un rango de frecuencia donde la luz no puede propagarse y el valor de la transmitancia es cero (Le y Nguyen-Tran, 2020). Dependiendo la modulación periódica del índice de refracción los cristales fotónicos se clasifican en unidimensionales (1D), bidimensionales (2D) y tridimensionales (Sakoda, 2004). Un cristal aperiódico (no periódico) es una estructura compleja que se caracteriza por tener diferente grado de orden y correlaciones espaciales, siendo así, un cuasicristal hasta un cristal amorfo un claro ejemplo de estas estructuras ordenadas y desordenadas respectivamente, con espectros difusos de difracción (Maciá 2005). Los cristales fotónicos constituidos por materiales con índices de refracción distinto colocados alternadamente (Segovia-Chaves y Vinck-Posada, 2018) siguiendo una secuencia cuasiperiódica como la de Fibonacci (Gellermann, Kohmoto, Sutherland y Taylor, 1994) son llamados cuasicristales (Chan, Chan y Liu, 1998.). Un cuasicristal es una estructura ordenada que carece de simetría de invariancia a lo largo de ciertas direcciones espaciales, pese a que es una estructura que llena todos los espacios ordenadamente no es periódica (Jin, Cheng, Man, Li, Zhang, Ban y Sun). Los medios ópticos aperiódicos generados por reglas matemáticas como la regla recursiva de una secuencia de Fibonacci en un cuasicristal han acaparado la atención de toda la comunidad científica dedicada al estudio de la óptica y electrónica, pues este tipo de cristales son de fácil fabricación, diseño y compatibilidad con la tecnología actual, lo que los hace ser más útil y productivos para la fabricación de aparatos electrónicos (Steurer y Sutter-Widmer, 2007). Encontrar las estructuras de bandas y las Brechas de Bandas Fotónicas (BBFs) lo podemos realizar a través del método de ondas planas (Johnson y Joannopoulos, 2001) (Sánchez y Orozco, 2016), discretización del dominio temporal (Zi, Wan y Zhang, 1998), elementos finitos (Bréchet, Marcou, Pagnoux y Roy, 2000). Sin embargo, en este trabajo se llevará a cabo el método de la matriz de transferencia (Chaves 2014), un procedimiento matemático ideal para el estudio de la propagación de ondas en sistemas unidimensionales (1D) (Rui, Wang, Lu y Yun ,2008). Con este método se reduce el problema de las fronteras a un simple producto de matrices que posteriormente, se llamará matriz de transferencia haciendo posible encontrar las amplitudes de transmisión y reflexión por medio de funciones de onda conocidas (Johnson y Joannopoulos, 2001).
La secuencia de Fibonacci en el campo de la fotónica es una sucesión utilizada para organizar las capas de los materiales que forman un cristal fotónico (Senechal 1996). La primera secuencia de Fibonacci se realizó en estudios de transporte de electrones por R. Merlin, K. Bajema et al. (Merlin, Bajema, Clarke, Juang y Bhattacharya 1985). Actualmente, F.Segovia-Chaves y H.Vinck-Posada, trabajan en cristales fotónicos unidimensionales con una secuencia de Fibonacci compuesta de materiales poliméricos (Segovia-Chaves y Vinck-Posada 2019). Es de resaltar que esta sucesión puede ser usada para cualquier tipo de material (polímeros, dieléctricos, semiconductores o superconductores) que compone un cristal fotónico (Janssen, Chapuis y De Boissieu 2007).
En este trabajo determinaremos el espectro de transmisión con incidencia oblicua para cada polarización TE(Transversal Eléctrica) y TM(Transversal Magnética), para ello, se solucionarán las ecuaciones de Maxwell mediante el método de la matriz de transferencia en un cristal fotónico unidimensional cuasiperiódico, cuyas capas se encuentran alternadas por una secuencia de Fibonacci.
Modelo Teórico:
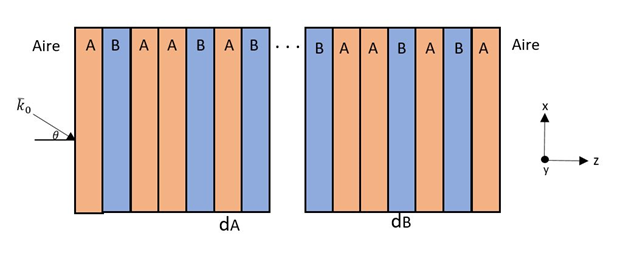
Fig.1. Estructura del Cuasicristal Fotónico -1D
En la fig.1. se muestra un cuasicristal rodeado de aire, organizado por una secuencia de Fibonacci que sigue la regla recursiva Sn= S(n-1) S(n-2) para (n≥2) con So=B que representa la capa de Polimetacrilato de Metilo (PMMA) y S1=A correspondiente a la capa de Poliestireno (PS) (Segovia-Chaves y Vinck-Posada, 2019). Teniendo en cuenta que, el cuasicristal posee un patrón homogéneo en el plano xy y su eje principal está en z (Segovia-Chaves y Vinck-Posada, 2019).
Mediante el método de la matriz de transferencia (Markos y Soukoulis, 2008) se determina el espectro de transmitancia de una onda electromagnética con ángulo incidente θ para la polarización TE (Transversal Eléctrica) y TM (Transversal Magnética).
Cada capa que compone el cuasicristal está representado por la matriz (Cabrera, López y Agulló-López, 2000):
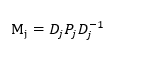
Donde la matriz de propagación P_j viene dada por:
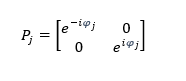
Al cambiar de capa, la onda electromagnética experimenta un cambio de fase
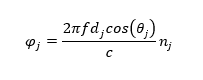
Donde, f representa la frecuencia de la luz, d_j y n_j son el espesor y el índice de refracción de capa del material, θ_j el ángulo con el cual incide la onda y c es la velocidad de la luz.
La matriz dinámica D_j para cada tipo de polarización está definida como:
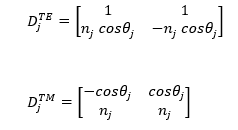
De tal manera, la matriz de transferencia total para la estructura cuasiperiódica está determinada por :
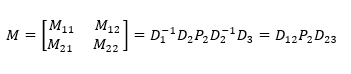
La transmitancia viene establecida por el elemento matricial m_11 de la matriz M
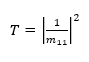
La constante dieléctrica de los polímeros direccionada sobre el eje principal va en función de la presión hidrostática orientada perpendicularmente al eje z

Donde, ∈_0 es la constante dieléctrica sin presión, P_11 y P_12 son las componentes del tensor de Pockels diferentes de cero, Y es el módulo de Young, v es el coeficiente de Poisson y P es la presión hidrostática aplicada.
En la tabla 1. se presentan los valores empleados para determinar la constante dieléctrica de cada polímero utilizado en las capas del cuasicristal.
Tabla 1. Valores elastoópticos
| Material | Y(GP_a) | v | P_11 y p_12 | Medio de índice de refracción en el rango THz |
|---|---|---|---|---|
| PMMA | 3.0303 | 0.37 | 0.300 y 0.297 | 1.484 |
| PS | 3.3000 | 0.35 | 0.320 y 0.310 | 1.578 |
Resultados:
a)
b)

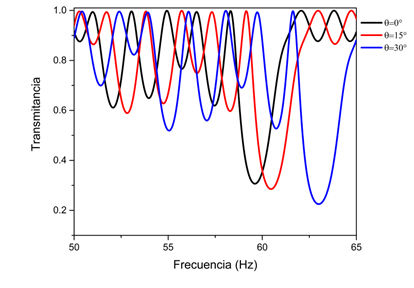
Fig.2. Espectro de transmitancia en función de la frecuencia para las secuencias a) S9 TE. b) S15 TM

Fig.3. Espectro de transmitancia de polarización TE y TM para la secuencia S11 con espesores idénticos dA=dB=1000 nm

Fig.4. Espectro de transmitancia en función de dA para la secuencia S8 con polarización TE, P= 100MPa

Fig.5. Espectro de transmitancia en función de dB para la secuencia S8 con polarización TM, P= 100MPa
Discusión:
En la Fig.2. se muestra el espectro de transmitancia encontrados a través del Método de la Matriz de Transferencia (MMT) para un cuasicristal, con espesores de capa iguales dA=dB=1000 nm. La secuencia de Fibonacci S9 (Fig.2.a) describe el comportamiento de la onda electromagnética con diferentes ángulos de incidencia para la polarización TE. Al aumentar el ángulo en una misma secuencia se observa un corrimiento del gap hacia frecuencias altas, estas variaciones tienen una considerable implicación en el cambio de la longitud de onda y en su frecuencia de acuerdo con la ley de Bragg-Snell. De esta manera, al existir un incremento en el ángulo de incidencia, la longitud de onda será más corta y, en consecuencia, tendrá una mayor frecuencia. La (Fig.2.b) presenta un espectro de transmisión con polarización TM para una secuencia de Fibonacci S15 a presión constante, en la cual, se evidencia la presencia de nuevas Brechas de Banda Fotónica (BBFs) al aumentar la secuencia, debido al incremento de capas en la estructura.
En la Fig.3. se presenta el comportamiento de la onda electromagnética con polarización TE y TM, se demuestra que el espectro de polarización TM cuenta con BBFs de menor valor en la transmitancia, sin embargo, para los gaps que se encuentran entre los (51.1 - 51.9 THz) y (57.9 – 58.2 THz) el espectro de transmisión para la polarización TE alcanza una transmitancia de ~0.2.
La Fig.4. muestra el resultado de la secuencia S8 para la polarización TE al variar el espesor de la capa A de (1000 a 2000 nm) con una presión y grosor de la capa B constante P= 100MPa y dA= 1000 nm respectivamente, las bandas fotónicas tienden hacia frecuencias bajas. En el espectro contemplamos una transmitancia de ~0 entre los (55.5 y 59 THz) al aumentar el espesor dA a ~1600 nm. Del mismo modo ocurre en la Fig.5. para la polarización TM, el espectro de transmisión evidencia zonas en que la transmitancia es 0 cuando la capa B aumenta su grosor de (1000 a 2000 nm), de esta manera se generan BBFs definidas y anchas que presentan un corrimiento hacia frecuencias bajas.
Referencias
Abirami, N., & Wilson, K. J. (2019). Investigation on photonic band gap of a magneto photonic crystal. Optik, 164092.
Bréchet, F., Marcou, J., Pagnoux, D., & Roy, P. J. O. F. T. (2000). Complete analysis of the characteristics of propagation into photonic crystal fibers, by the finite element method. Optical Fiber Technology, 6(2), 181-191.
Cabrera, J. M., López, F. J., & Agulló-López, F. (2000). Óptica electromagnética: volI: fundamentos. Ed Addison Wesley, 7.
Chan, Y. S., Chan, C. T., & Liu, Z. Y. (1998). Photonic band gaps in two dimensional photonic quasicrystals. Physical Review Letters, 80(5), 956.
Chaves, F. S. (2014). Flujo de Energía Reflejado y Transmitido en Cristales Fotónicos Unidimensionales. Revista Facultad de Ciencias Básicas, 10(2), 158-167.
Dal Negro, L. (Ed.). (2013). Optics of aperiodic structures: fundamentals and device applications. CRC Press.
Elmore, W. C., & Heald, M. A. (1985). Physics of waves. Courier Corporation.
Gellermann, W., Kohmoto, M., Sutherland, B., & Taylor, P. C. (1994). Localization of light waves in Fibonacci dielectric multilayers. Physical review letters, 72(5), 633.
Janssen, T., Chapuis, G., & De Boissieu, M. (2007). Aperiodic crystals: from modulated phases to quasicrystals (Vol. 20). Oxford University Press.
Jin, C., Cheng, B., Man, B., Li, Z., Zhang, D., Ban, S., & Sun, B. (1999). Band gap and wave guiding effect in a quasiperiodic photonic crystal. Applied physics letters, 75(13), 1848-1850.
Johnson, S. G., & Joannopoulos, J. D. (2001). Photonic crystals: the road from theory to practice. Springer Science & Business Media.
Johnson, S. G., & Joannopoulos, J. D. (2001). Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Optics express, 8(3), 173-190.
Maciá, E. (2005). The role of aperiodic order in science and technology. Reports on Progress in Physics, 69(2), 397.
Markos, P., & Soukoulis, C. M. (2008). Wave propagation: from electrons to photonic crystals and left-handed materials. Princeton University Press.
Meade, R. D., Winn, J. N., & Joannopoulos, J. D. (1995). Photonic crystals: Molding the flow of light.
Merlin, R., Bajema, K., Clarke, R., Juang, F. Y., & Bhattacharya, P. K. (1985). Quasiperiodic gaas-alas heterostructures. Physical review letters, 55(17), 1768.
Le, N. D., & Nguyen-Tran, T. (2020). Simulation of coupling optical modes in 1D photonic crystals for optoelectronic applications. Journal of Science: Advanced Materials and Devices.
Rui, X., Wang, G., Lu, Y., & Yun, L. (2008). Transfer matrix method for linear multibody system. Multibody System Dynamics, 19(3), 179-207.
Saleh, B. E., & Teich, M. C. (2019). Fundamentals of photonics. john Wiley & sons.
Sakoda, K. (2004). Optical properties of photonic crystals (Vol. 80). Springer Science & Business Media.
Sánchez, A., & Orozco, S. (2016). Elasto-optical effect on the band structure of a one-dimensional photonic crystal under hydrostatic pressure. JOSA B, 33(7), 1406-1410.
Segovia-Chaves, F., & Vinck-Posada, H. (2018). Dependence of the defect mode with temperature, pressure and angle of incidence in a 1D semiconductor-superconductor photonic crystal. Physica C: Superconductivity and its Applications, 553, 1-7.
Segovia-Chaves, F., Vinck-Posada, H., Dhasarathan, V., & Rajan, M. M. (2019). Transmittance spectrum in a 1D photonic crystal composed fused silica and sea water. Optik, 185, 930-935.
Segovia-Chaves, F., & Vinck-Posada, H. (2019). Transmittance spectrum in a 1D photonic crystal with a Fibonacci sequence composed of polymer materials. Optik, 196, 163141./p>
Segovia-Chaves, F., & Vinck-Posada, H. (2019). Transmittance spectrum of a superconductor-semiconductor quasiperiodic one-dimensional photonic crystal. Physica C: Superconductivity and its Applications, 563, 10-15.
Senechal, M. (1996). Quasicrystals and geometry. CUP Archive.n a 1D photonic crystal with a Fibonacci sequence composed of polymer materials. Optik, 196, 163141.
Steurer, W., & Sutter-Widmer, D. (2007). Photonic and phononic quasicrystals. Journal of Physics D: Applied Physics, 40(13), R229.
Yablonovitch, E. (1987). Inhibited spontaneous emission in solid-state physics and electronics. Physical review letters, 58(20), 2059.
Yariv, A., & Yeh, P. (1984). Optical waves in crystals (5). New York: Wiley.
Zi, J., Wan, J., & Zhang, C. (1998). Large frequency range of negligible transmission in one-dimensional photonic quantum well structures. Applied physics letters, 73(15), 2084-2086.