Julián Cantor1 y Sergio Rivera2
La optimización del costo de la energía por medio de la ubicación de turbinas en el diseño de parques eólicos es un problema que en las últimas dos décadas ha tomado importancia y que para resolverlo se han aplicado metaheurísticas de alto nivel. En el presente artículo, se detalla un modelo de parque eólico y se destaca la importancia del diseño óptimo de parques eólicos proponiendo la mejor ubicación de las turbinas en un layout. El layout hace referencia a la discretización del terreno de búsqueda en una cuadricula por medio de un arreglo de coordenadas cartesianas para su posterior codificación en una cadena binaria: un uno representa una turbina a instalar en la posición indicada y un cero indica lo contrario. De esta manera, en este artículo se muestran las diferentes metaheurísticas aplicadas para resolver este problema y como estas han tenido mejores resultados que técnicas empíricas utilizadas tradicionalmente. Por otro lado, se introduce una metaheurística de alto nivel basada en la caza de la larva de la hormiga león (Ant Lion Optimizer) y se muestra una técnica derivada de este trabajo que utiliza variables binarias (Binary Ant Lion Optimizer). Por último, se introduce un problema de diseño de parque eólico. Este problema utiliza un evaluador del costo de la energía que cuenta con modelos de la distribución del viento, del efecto estela y de la función de costos. Este problema se estudió para determinar el menor costo por medio de heurísticas de bajo nivel y por medio de metaheurísticas; se encontró que el mejor resultado se daba al utilizar el algoritmo de variables binarias con heurísticas de bajo nivel.
Palabras clave: optimización; diseño; parques eólicos; metaheurísticas; algoritmos binarios.
Optimization of energy costs by the location of turbines in the wind farm design is a problem that, in the last two decades, has become important. In order to solve it, Metaheuristics techniques of high level have been applied. In this article, an Eolic park model is detailed, and the importance of an optimal design of wind farms is stressed proposing the best location of the turbines in a layout. The layout refers to the discretization of the search field in a grid by means of a Cartesian coordinate arrangement for later encoding in a binary string: A one represents a turbine to be installed in the indicated position and a zero indicates otherwise. As such, this article shows the different metaheuristics applied to solve this problem and how these have had better results than empirical techniques traditionally used. On the other hand, a high level metaheuristic technique based on the hunting of the lion ant larva (Ant Lion Optimizer) and a technique derived from this work that uses binary variables (Binary Ant Lion Optimizer) are used. Finally, a wind farm design problem is introduced. This problem uses an energy cost estimator that has models of wind distribution, wake effect, and cost function. This problem was studied to determine the lowest cost through low level heuristics and through metaheuristics; the best result was given by using the algorithm of binary variables with low level heuristics.
Keywords: optimization; design; eolic park; metaheuristic; binary algorithms.
La obtención de electricidad por medio de fuentes renovables es un tema de alta importancia de cara al futuro. Una de las fuentes renovables de mayor impacto a nivel global es la energía eólica. Este tipo de energía aprovecha la velocidad del viento para producir energía eléctrica por medio del movimiento de turbinas.
La capacidad instalada a nivel mundial de generación eólica (Onshore y Offshore) ha crecido cerca de 50 veces en las últimas dos décadas de 7.5 GW en 1997 a más de 371 GW en 2014 (IRENA, 2016). Este notable crecimiento se debe a impactos económicos y técnicos. En el aspecto técnico, se destaca el uso de turbinas con mayores potencias.
En el aspecto económico, se destaca la economía de escalas. Esto se logra cuando las turbinas eólicas se instalan en grandes grupos sobre amplias extensiones de terrenos, a este tipo de lugares se le conoce como parques eólicos. No obstante, la instalación de muchas turbinas presenta reducción de la capacidad instalada, esto se conoce como efecto estela (Samorani, 2013).
El efecto estela (wake effect) se produce por la turbulencia o estela que se genera en el viento cuanto éste atraviesa una turbina, en consecuencia, si una segunda turbina se ubica dentro del área de estela de la primera, la capacidad instalada se ve afectada.
En parques eólicos de gran tamaño el efecto estela produce considerables pérdidas de potencia que deben ser minimizadas (Samorani, 2013). Una forma de hacerlo consiste en posicionar adecuadamente las turbinas de manera irregular de tal forma que la interferencia de una en otra sea la menor posible.
Este proceso se conoce como Problema de Optimización de Diseño de Parques Eólicos (Wind Farm Layout Optimization Problem-WFLOP) y consiste en la búsqueda de la mejor posición de turbinas que maximice la producción de energía, considerando restricciones por efecto estela.
Actualmente, el diseño de parques eólicos busca integrar cada vez más restricciones haciendo que el problema se vuelva más complejo y difícil de resolver. Por ejemplo, los parques eólicos son explotados más extensamente en onshore, lo que conlleva a que la instalación coexista con seres humanos.
De manera adicional, en el diseño de parques eólicos el clima es un factor importante. La intensidad y frecuencia del viento no son variables continuas, al contrario, son variables probabilísticas que no son fáciles de estimar.
Todos estos aspectos como lo son la variabilidad del viento, el efecto estela, los impactos ambientales y el posicionamiento de turbinas hacen que el problema de optimización en el diseño de parques eólicos sea un problema complejo y difícil de resolver por medio de técnicas tradicionales. En el estado de la técnica actual para resolver el problema mencionado, los autores han aplicado técnicas metaheurísticas de alto nivel para encontrar soluciones de buena calidad.
En trabajos presentados anteriormente Mosetti et al (1994); Gradya et al (2004); Bilbao & Alba (2009); Eroglu & Ulusam (2012); Saavedra-Moreno et al (2011) se ha demostrado la ventaja de técnicas metaheurísticas frente a el uso de técnicas empíricas y métodos aleatorios de posicionamiento. Entre las principales metaheurísticas aplicadas en el problema de optimización en el diseño de parques eólicos se encuentran los Algoritmos Genéticos (AG), la Optimización por Enjambre de Partículas (OEP) y la Optimización por Colonia de Hormigas (OCH).
De esta manera, el presente artículo presenta el abordaje propuesto discutiendo en la sección 2 el modelo de parque eólico utilizado. En la sección 3 se resume el uso de técnicas heurísticas y metahurísticas para el diseño de parques eólicos. En la sección 4 se introduce la metaheurítisca de alto nivel utilizada para resolver el problema. En la sección 5 se obtienen los resultados que se obtuvieron al aplicar heurísticas y la metaheurística de alto nivel. Finalmente, en la sección 6 se dan las conclusiones.
Las turbinas de viento consideradas para la granja de vientos son homogéneas, es decir, todas tienen la misma curva de potencia P= f(v) como función, donde v es la velocidad del viento en el rotor de la turbina con una altura fija y P es la potencia de salida de la turbina. El nacelle o góndola de una turbina eólica usualmente se controla para que la dirección del viento sea perpendicular al rotor (Kusiak & Song, 2010).
La distribución del viento está basada en el modelo expuesto por (Kusiak & Song, 2010). La dirección del viento v, a una localización, altura y dirección sigue una distribución Weibull de la siguiente forma.
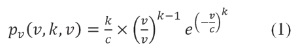
Donde:
K es el parámetro de forma, c es el parámetro den escala y pv es la función de densidad de probabilidad.
A una altura, la velocidad del viento (v) (un parámetro de la distribución de Weibull) es una función continua de la dirección del viento è, es decir, que tanto k como c, son funciones del ángulo para el intervalo de 0 a 360°. è presenta distribución de probabilidad continua. Esta distribución del viento es razonable para terrenos planos y para parques eólicos que no abarquen una gran cantidad de terreno (Kusiak & Song, 2010).
El efecto estela también es conocido en la literatura como efecto sombra o Wake effect. En (Kusiak & Song, 2010) se introduce un modelo para efecto estela que se explica a continuación. Para una dirección particular, dada una turbina i localizada en xi y yi, un número de otras turbinas afecta el viento que experimenta. Esto se llama el efecto estela. La forma en que afecta la distribución, dirección y velocidad del viento se determina mediante un modelo de estela.
Si una turbina localizada en (xi, yi) está en la estela de otra turbina localizada en (xj, yj), el viento en la localización dada es modificado mediante el cambio del parámetro c de la distribución de Weibull, lo que da lugar a un parámetro nuevo ci. La magnitud de ci depende de la distancia Euclidiana entre i y j.
El terreno se dispone de tal forma que no es un lugar donde se pueda construir de forma continua, es decir, el mismo presenta en la superficie disrupciones que se deben a lagos, montañas y en general a la topografía del lugar.
El objetivo consiste en minimizar el costo de la energía eléctrica anual que se puede obtener en un escenario de viento dado por medio de turbinas eólicas. La función objetivo que describe el costo de la energía se presenta a continuación y fue introducida en el marco de la segunda edición del concurso denominado Wind Farm Layout Optimization Competition (WFLO, 2015).
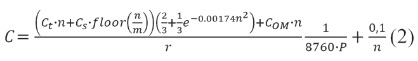
Donde cada elemento de la ecuación (2) se describe a continuación:
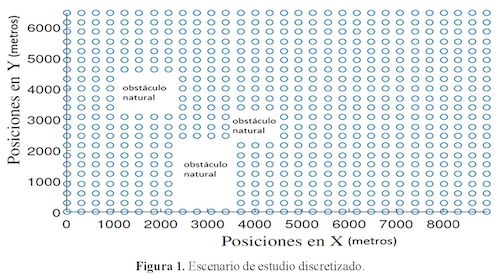
La forma del terreno corresponde a un plano x-y dividido en cuadricula. En la figura 1 se muestra el escenario considerado en el presente trabajo. Cada o es una posición definida mediante coordenadas (xi, yi) donde se considera la instalación de la turbina. Si en una posición se instala una turbina, hay un vector que guarda esa posición como un uno, en caso contrario, en el vector se almacena un cero.
Debido a la complejidad del problema de optimización de diseño de parques eólicos, se hace necesario utilizar métodos diferentes a los tradicionales para encontrar soluciones de buena calidad. Para solucionar este problema, la mayor parte de técnicas utilizadas de manera tradicional han sido las metaheurísticas.
En trabajos presentados anteriormente (Mosetti et al., 1994); (Gradya, et al., 2004); (Bilbao & Alba, 2009); (Eroglu & Ulusam, 2012); (Saavedra-Moreno, et al., 2011) se ha demostrado la ventaja de las metaheurísticas frente a el uso de técnicas empíricas y métodos aleatorios de posicionamiento. Entre las principales metaheurísticas aplicadas en el problema de optimización en el diseño de parques eólicos se encuentran los Algoritmos Genéticos (AG), la Optimización por Enjambre de Partículas (OEP) y la Optimización por Colonia de Hormigas (OCH).
A continuación, se hace un repaso de las heurísticas y las metaheurísticas y, se muestran algunos resultados obtenidos en el problema de optimización de diseño de parques eólicos.
Muchos de los problemas que tienen aplicación en la ingeniería no se pueden resolver aplicando métodos de optimización tradicionales. Las causas de esto son la complejidad matemática y la numerosa cantidad de variables y restricciones (Mosetti, et al., 1994); (Gradya, et al., 2004); (Bilbao & Alba, 2009); (Gallego, et al., 2015).
Dentro del conjunto de técnicas disponibles para encontrar soluciones de buena calidad con esfuerzos computacionales aceptables se encuentran las técnicas heurísticas.
Las heurísticas son empleadas para resolver problemas sin un riguroso análisis formal, basados en la experiencia de quien trabaja el problema. Estas técnicas en ocasiones resuelven problemas de tamaño pequeño y baja complejidad.
Un algoritmo heurístico es una técnica de exploración de soluciones que utilizan un conjunto de pasos que encuentran soluciones de buena calidad y de manera rápida. Las técnicas heurísticas avanzan hacia soluciones de mejor calidad y cuando no la encuentran, finaliza el proceso de búsqueda. Algunas de las técnicas más conocidas son (Mosetti, et al., 1994); (Gradya, et al., 2004); (Bilbao & Alba, 2009); (Gallego, et al., 2015).
1. Algoritmos heurísticos constructivosEn este algoritmo paso a paso, se van adicionando componentes individuales a la solución hasta encontrar una que sea factible. El más conocido es el algoritmo greedy (goloso).2. Algoritmos de descomposición y división. La descomposición separa el problema en pequeños problemas de menor complejidad. Se busca simplificar el proceso de solución.3. Algoritmos de reducción.Se intenta reducir el problema encontrando características comunes de las variables.4. Algoritmos de manipulación de modelo. Se utilizan modelos relajados del modelo inicial para encontrar soluciones relajadas que sirvan de insumo como solución al problema.5. Algoritmos de búsqueda usando vecindad. Estos métodos inician el proceso de solución a partir de una solución inicial, factible y, usando un mecanismo de transición adecuado pasan a una solución vecina de mejor calidad. Este proceso se repite, solución tras solución hasta que no se encuentra una de mejor calidad.6. Hiperheurísticas. Las Hiperheurísticas (Gallego, et al., 2015) se conciben como una herramienta de alto nivel que permiten controlar adaptativamente varias heurísticas o metaheurísticas con bajo nivel de conocimiento del problema, de forma que aplicando solo heurísticas fáciles de usar se pueden conseguir soluciones equiparables a las obtenidas por medio de metaheurísticas.
Las metaheurísticas (Mosetti, et al., 1994); (Gradya, et al., 2004); (Bilbao & Alba, 2009); (Gallego, et al., 2015); (Saavedra-Moreno, et al., 2011); (Eroglu & Ulusam, 2012) son el conjunto de estrategias que aplican procedimientos heurísticos de alto rendimiento para resolver problemas complejos. El prefijo ‘meta' implica que una metaheurística va más allá de una heurística en la búsqueda de soluciones de buena calidad.
Las metaheurísticas se diseñan para no caer en óptimos locales por medio de mecanismos de cambio. A partir de una solución inicial se busca soluciones vecinas hasta que se cumpla un criterio de parada.
El primer trabajo relacionado con el diseño de parques eólicos y la aplicación de Metaheurísticas se dio con el uso de Algoritmos Genéticos (Mosetti, et al., 1994), (Samorani, 2013).
Este documento fue introducido en 1994 y ha sido punto de partida para otros trabajos que tratan la temática del problema de diseño de parques eólicos. En Mosetti et al (1994) se determinó la posición de turbinas eólicas con unas condiciones de viento predefinidas, con el fin de maximizar la energía y minimizar los costos de instalación.
Sin embargo, a pesar que la idea central de la investigación es la mencionada anteriormente, los autores realizan varias consideraciones en el modelo que desarrollan. Esto se debe a que también buscaban evaluar las ventajas que trae consigo el uso de algoritmos genéticos en el diseño de parques eólicos.
Dentro de las consideraciones que tienen, están, por ejemplo, la influencia que tienen las turbinas entre sí, la variabilidad del viento en los tres escenarios que consideran y el objetivo central del problema, extraer la máxima cantidad de energía con los mínimos costos de instalación.
Para poder realizar esto, los autores basan su trabajo en dos algoritmos distintos. El primero, evalúa el escenario y determina el desempeño del parque mientras que el segundo es un algoritmo genético que determina la ubicación de las turbinas.
El modelo de evaluación de parques eólicos utiliza una serie de pasos para calcular la cantidad de energía anual producida.
En la segunda parte se hace uso de un GA. La idea detrás de esta metaheurística es el proceso de evolución biológica por medio de la transformación de un código genético.
En la naturaleza, la reproducción de un individuo toma lugar cuando la información genética de dos individuos (almacenada en un cromosoma) es utilizada para llegar a uno nuevo. La supervivencia de la especie se garantiza debido a que el mejor individuo tiene más probabilidades de sobrevivir.
Para construir un nuevo cromosoma existen tres procesos: mutación aleatoria, intercambio genético entre los padres e inversión de la cadena cromosómica. En el algoritmo genético desarrollado utilizan el intercambio genético entre dos individuos y la mutación aleatoria. Estos dos procesos son hechos de manera aleatoria y están ligados a una función de probabilidad.
Como conclusión, afirman que este nuevo enfoque ha mostrado su factibilidad y que puede ser aplicado a modelos de parques más sofisticados. De igual forma, aunque consideraron un solo tipo de turbina, prevén mejores resultados si se utiliza mucha más información de la misma, así como una función de costos más completa.
Este tipo de algoritmo ha sido ampliamente utilizado en la búsqueda de la mejor posición de turbinas en el diseño de parques eólicos (Samorani, 2013); (Mosetti, et al., 1994); (Bilbao &Alba, 2009).
Esta técnica conocida por sus siglas en inglés como PSO (Particle Swarm Optimization) es una meta-heurística de optimización matemática basada en el comportamiento social de los enjambres o manadas.
Con base en esto, se definió que cada individuo puede modificar su comportamiento basado en tres factores (Kennedy & Eberhart, 2009).
De esta manera, el objetivo es que todos los pobladores del problema alcancen un óptimo global, basado en dos comportamientos de cada individuo (Bilbao & Alba, 2009); (Gallego, et al., 2015); (Kennedy & Eberhart, 2009).
Los individuos tienden a moverse hacia donde el líder se dirige, no obstante, los individuos también pueden tomar decisiones basados en su conocimiento histórico.
Dentro de los trabajos basados en la metaheurística PSO para resolver el problema de optimización de parques eólicos se tiene el trabajo realizado en Bilbao & Alba (2009) en este trabajo se encontró la menor cantidad posible de las turbinas en un parque eólico de tal forma que los costos de instalación disminuyeran.
Para esto, ellos tienen en consideración un modelo para el efecto estela, un modelo de la potencia extraída de la granja, un modelo de costos y las técnicas metaheurísticas CHC (una metaheurística derivada de los algoritmos genéticos) y GPSO (Bilbao & Alba, 2009).
El modelo del efecto estela considera la conservación del momentum angular. El modelo de potencia tiene la forma de una función definida por tramos, donde uno de los tramos comprendidos depende de la velocidad del viento sobre la turbina. La potencia total generada es la suma de las potencias de las n turbinas instaladas.
La clave en el GPSO consiste en usar una recombinación multi-parental de partículas que sustituye el movimiento clásico en PSO, basado en la actualización de velocidad y posición de las partículas. Para evaluar el rendimiento de los dos algoritmos se consideraron 3 escenarios. Cada escenario que se considero es de viento uniforme que viene del norte, con diferentes velocidades para cada caso.
A modo de conclusión se observó ambos algoritmos conducen a resultados aceptables y, que se obtuvieron resultados similares de trabajos previos. También se concluyó que para futuros trabajos es necesario considerar modelos adicionales de parques eólicos que incluyan más factores.
Ant Colony Optimization o ACO es una técnica de optimización metaheurística que fue introducida en 1992 por Marco Dorigo (Gallego, et al., 2015). Esta técnica se basa en el comportamiento que tienen las hormigas en una colonia con la búsqueda de alimento.
La búsqueda de alimento en una colonia de hormigas, está relacionada con la comunicación que establecen las hormigas por medio de feromonas. Estas sustancias químicas les permiten establecer rutas cortas entre la comida y el nido. Dicha característica de establecer rutas químicas se modela y extrapola para resolver problemas de optimización con variables discretas (Blum, 2005). El ACO aplicado al problema de optimización de diseño de parques eólicos se aplicó en (Eroglu & Ulusam, 2012). En este trabajo, se presenta un algoritmo de colonia de Hormigas para maximizar la energía de un parque.
En este algoritmo, los autores consideran pérdidas de energía por efecto estela, para lo cual utilizan tres escenarios diferentes de viento y comparan su trabajo con el algoritmo genético implementado (Kusiak & Song, 2010).
El problema tiene las siguientes propiedades:
El algoritmo implementado cumple los siguientes pasos:
El algoritmo de Colonia de Hormigas para este trabajo fue modificado para tratar el problema de manera continua. El algoritmo fue aplicado para optimizar la posición de las turbinas de tres escenarios diferentes. Finalmente, los autores concluyen que los resultados del algoritmo de colonia de hormigas fueron mejores que los obtenidos a partir de algoritmos genéticos. De forma paralela, ese algoritmo implementado tiene la ventaja de escapar de máximos locales, por lo que considera abarca más espacios de búsqueda.
A continuación, se introduce el método propuesto basado en la larva de la hormiga león para solucionar el problema. Este insecto, también conocido como Myrmeleon, hace parte de la familia Myrmelentidae y se encuentran ampliamente en las regiones más calientes del mundo. La hormiga león tiene dos etapas durante su vida: larvaria y adulta (Mirjalili, 2015).
Este insecto es descrito mejor por su nombre de ‘hormiga león' debido a la técnica que utilizar para cazar otros insectos en su estado larvario. Este proceso puede describirse en las siguientes etapas: La hormiga león hace pozos de embudo en arena suave cavando hacia atrás (Mirjalili, 2015).
En este proceso, hace senderos espirales de forma de embudo de diferentes tamaños. Una vez la trampa ha sido construida, la larva espera pacientemente en el fondo de la trampa por su presa. Al deslizarse por el embudo, la presa es captada por la hormiga león (Mirjalili, 2015).
Si se llegara a presentar un intento de fuga del embudo, la larva arroja arena al borde de la trampa para impedir que la presa se escape.
En el 2015 se incluyó a la gama de metaheurísticas disponibles un algoritmo basado en la caza de la larva de la hormiga león. El algoritmo fue propuesto en (Mirjalili, 2015).
Posteriormente, en Rivera & Gutiérrez (2017) se modificó el algoritmo para trabajar con variables binarias discretas. Éste algoritmo obtuvo buenos resultados para el problema de optimización de diseño de parques eólicos.
El algoritmo ALO recrea la interacción entre la larva de la hormiga león y otras hormigas en la trampa. Para modelar tales interacciones, se requiere que las hormigas se muevan por el espacio de búsqueda, de tal forma que la hormiga león pueda cazarlas tal como se describió anteriormente. Dado que las hormigas hacen movimientos estocásticos en la búsqueda por comida, se selecciona caminos aleatorios para modelas este comportamiento (Mirjalili, 2015); (Rivera & Gutiérrez, 2017). Él modelo tiene la siguiente presentación.
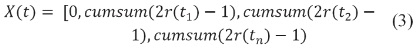
Donde la función cumsum calcula la suma acumulada de la función objetivo, n es la máxima cantidad de iteraciones, t muestra la iteración de estudio y r(t) es una función estocástica definida como sigue:
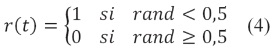
En la ecuación (4) rand es una función que representa un número aleatorio generado con distribución uniforme entre el intervalo [0,1].
El comportamiento que tienen las hormigas es similar al que siguen las partículas en el Algoritmo de Cumulo de Partículas (PSO) o en el de los individuos en Algoritmos Genéticos (GA).
Para resolver el problema, cada posición de las hormigas es almacenada en una matriz. Si se dice que Aij es el valor de la dimensión i-ésima de la hormiga j-ésima, se evalúa la función objetivo como se hace en (5).
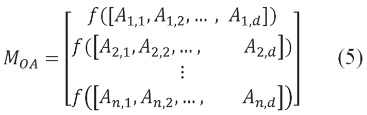
De igual manera, se puede guardar los resultados obtenidos de la función objetivo f, para las diferentes posiciones consideradas de la hormiga león.
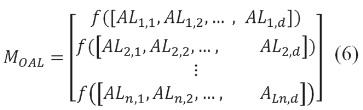
A continuación, se explica el modelo utilizado bajo las condiciones explicadas anteriormente:
Todos los caminos aleatorios están basados en la ecuación (3), las hormigas actualizan sus posiciones mediante caminos aleatorios en cada etapa de la optimización. Sin embargo, la ecuación (3) no puede ser directamente aplicada para actualizar la posición de las hormigas.
Los caminos aleatorios deben restringirse y normalizarse para evitar que las hormigas se salgan del espacio de búsqueda.
Los caminos aleatorios de las hormigas se ven afectados por las trampas de las hormigas león.
Para modelar las capacidades de caza de la hormiga león, se emplea el modelo de “Rueda de Ruleta” la cual permite seleccionar el pozo donde ha quedado atrapada la hormiga.
Las hormigas león están en la capacidad de construir trampas proporcionales a su fitness, se requiere que las hormigas puedan moverse aleatoriamente. Sin embargo, las hormigas león disparan arena afuera del centro del embudo una vez que se dan cuenta que la hormiga está en la trampa.
La caza finaliza cuando una hormiga alcanza el fondo del pozo y es atrapado por las mandíbulas de la hormiga león. Después de esto, la hormiga león se alimenta de la hormiga.
Finalmente, la hormiga león esta lista para consumir otra presa. Para simular esto, se le asigna una nueva posición a la hormiga león con el fin de aumentar su probabilidad de atrapar a una presa:
El elitismo es una característica importante de los algoritmos de evolución que permite guardar las mejores soluciones obtenidas en cualquier etapa de la optimización. En el algoritmo la mejor hormiga león es almacenada en cada iteración y considerada élite.
Después de definir las características del código, el algoritmo trabaja bajo 3 funciones de listas ordenadas que aproximan al óptimo global como una función:
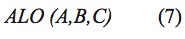
Donde A es una función que genera los valores iniciales de las soluciones, B manipula la población inicial prevista por la función A y C que se activa cuando el criterio de finalización se cumple. Las funciones A, B, C se definen de la siguiente manera
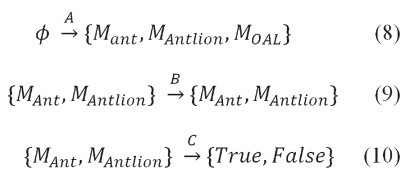
Donde Mant es la matriz de posición de las hormigas, MAntlion incluye la posición de las Hormigas León, MOA contiene los valores óptimos de las hormigas y MOAL tiene los valores óptimos de las Hormigas León.
Cuando los algoritmos de optimización, especialmente aquellos algoritmos bio-inspirados, buscan el mínimo de las funciones estos pueden estar buscando alrededor de mínimos locales, lo que no permite buena precisión en los resultados (Rivera & Gutiérrez, 2017). Sumado a esto, el algoritmo puede converger a valores que estén fuera de su rango de búsqueda. Al utilizar un sistema binario, cualquier número se puede representar. Para ello se utilizan 15 bits dados por (Mirjalili, et al., 2014).
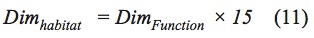
En la ecuación (11) Dimhabitat indica las dimensiones de cada uno de los habitad que se encuentra dentro del sistema y DimFunction las dimensiones de cada función.
Se tienen entonces, que las dimensiones de las partículas son de 75 para funciones de dimensión 5 y 450 para funciones de dimensión 30 (Rivera & Gutiérrez, 2017). En el desarrollo binario se tiene en cuenta cada una de las dimensiones binarias.
Para describir el desarrollo binario, se debe tener en cuenta que, para cada uno de las dimensiones de las funciones, se realiza una conversión binaria de 15 bits para cada una de ellas.
Después de ello, se toma el primer bit de cada uno de las transformaciones las cuales definirán el signo de la misma, en caso de ser “0” se dice que es negativa, en caso de ser “1” se dice que es positiva.
Después de ello se toma cada uno de los XBk y se convierten de binario a decimal con el respectivo signo, teniendo n valores que serán computadas dentro del algoritmo.
Para modificar el Ant Lion Optimizer de variables continuas a variables discretas se utilizó el aporte hecho en (Rivera & Gutiérrez, 2017). Sin embargo, se efectúo una alteración en el rango de búsqueda de las funciones y se incrementaron los valores de trabajo de acuerdo a las dimensiones que cada función tiene (Rivera & Gutiérrez, 2017).
La diferencia de este algoritmo con el BBO es que el ALO no posee función de migración por lo que no es necesario adicionar elementos al algoritmo (Rivera & Gutiérrez, 2017).
Para solucionar el problema de optimización del diseño de parques eólicos, en un principio se abordó el problema por medio de técnicas heurísticas. Estas técnicas, no se basan en métodos clásicos de optimización matemática, al contrario, aplican reglas aleatorias y se evalúa de manera analítica las soluciones obtenidas.
Posteriormente, se aplicó una metaheurística de alto nivel denominada Ant Lion Optimizer (Mirjalili, 2015), con la modificación propuesta en (Rivera & Gutiérrez, 2017) para manejo de variables binarias. Este algoritmo se denomina BALO o Binary Ant Lion Optimizer.
Finalmente se aplicaron algunas heurísticas utilizadas en la primera parte y se encontró que el costo de kilovatio hora mejoraba en comparación a los resultados obtenidos en Binary Ant Lion Optimizer.
En la sección 2 se explicó que la forma de representar la instalación de una turbina es mediante variables binarias, donde un uno representa la instalación de una turbina y un cero indica contrario. Esta información se almacena en un vector donde cada posición del vector representa una posición del terreno discretizado. En el problema de estudio abordado en este trabajo, se dispone de 607 posiciones posibles para instalar una turbina (Figura 1).
De tal forma, en el primer escenario P1 (ecuación (12)) se consideraron todas las turbinas instaladas y la función objetivo obtuvo un costo de C = 12,5381.
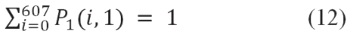
Posteriormente, el problema se abordó por medio de un análisis de sensibilidad sobre el vector P1, con el fin de determinar cómo se comportaba el costo del kWh. El análisis de sensibilidad es un término adaptado de la evaluación de proyectos, donde se realizan cambios aleatorios en algunas variables importantes (tasa de crecimiento, costos, inversión inicial, duración, etcétera) para observar el comportamiento de los flujos de caja y el VAN. Este análisis se efectúa para encontrar mejores estimaciones sobre un proyecto (Coss, 1981).
En el primer análisis de sensibilidad para el vector P1, se fueron apagando una a una de cada una de las casillas de la turbina, mientras las demás se mantenían según la condición inicial. El vector obtenido se denominó P2. Con el nuevo escenario P2 se calculó la función objetivo. Los casos más representativos se muestran en la tabla 1.
Los datos en la tabla 1 están organizados de menor a mayor. Las diferencias no son apreciables debido a la aproximación que utiliza el software de 4 cifras decimales después de la coma. Con base en cada caso de la columna 1 se propuso un segundo análisis de sensibilidad.
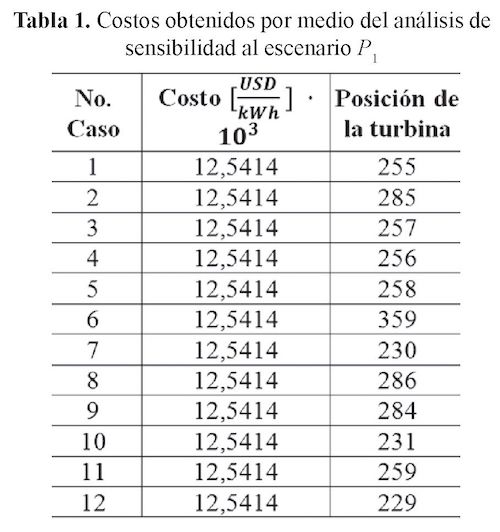
El segundo análisis de sensibilidad consistió en modificar el vector del escenario P2 (un vector P2 para los 12 casos de la columna 1 de la tabla 1). A los diferentes vectores P2, se les modificó una segunda turbina del estado 1 al estado 0, de cada una de sus casillas y se evaluaba el costo. Con este análisis se obtuvo un vector P3.
Se pudo determinar que el costo de los vectores P3 aumentaban respecto al caso inicial encontrado con el vector P2. Los resultados de mayor calidad están registrados en la tabla 2.
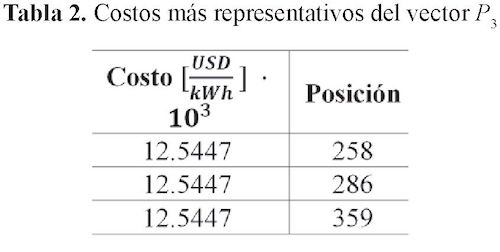
En la figura 2 se puede ver la variación en por unidad de los costos (costo base de 12,5381), entre los escenarios obtenidos con el vector P3 y el costo obtenido por el escenario P2. Se encontró que, al no considerar la instalación de una turbina, en cada uno de los 12 casos, las variaciones en los costos entre cada caso no eran significativas.

El cuarto análisis de sensibilidad mantuvo la mecánica utilizada hasta el momento: se apagaba de manera aleatoria un número fijo y determinado de turbinas y se creaba un nuevo escenario P4. Cada escenario P4 planteado de forma aleatoria, se evaluaba y se evaluaba si el costo era mejor al inicial de 12.5414 obtenido hasta el momento (escenario P1).
El algoritmo se programó con un criterio de parada de 605 veces debido a que, para un número mayor de 2 turbinas apagadas, los escenarios posibles son del orden de 2606, por lo que excede el tiempo computacional y también, debido a los criterios explicados en la sección del uso de técnicas heurísticas y metahurísticas para el diseño de parques eólicos (parámetros heurísticos).
Las condiciones iniciales del código en el cuarto análisis de sensibilidad consistieron en el vector binario P1, con 606 turbinas instaladas. La única turbina sin instalar se ubicó en la posición 255 (el mejor resultado obtenido en el primer análisis de sensibilidad (Tabla 1). Posteriormente, de manera aleatoria, se seleccionaba una cantidad conocida de turbinas entre 1 y 607, que iba aumentando en cada iteración. La cantidad de turbinas se fijó entre 3 y 200. Por cada iteración se estableció un criterio de parada de 605 iteraciones. Este algoritmo se muestra en la figura 3.
Del algoritmo de la figura 3 se obtuvieron un total de 1674 escenarios favorables de 119185 que se analizaron en total. En cada iteración propuesta, se guardaba el mejor resultado favorable y que fuera menor a un costo propuesto de 13. De esa forma, se descartaron 119021 escenarios que eran inferiores a los 1674 logrados (criterio de elitismo).
En la figura 4 se puede ver la distribución que se obtuvo de las diferentes turbinas. El eje de las abscisas representa cada una de las posibles posiciones posibles, 607 para este escenario de viento, por otro lado, el eje de las ordenadas tiene normalizada la cantidad de veces que se consideró instalar una turbina en ese lugar.
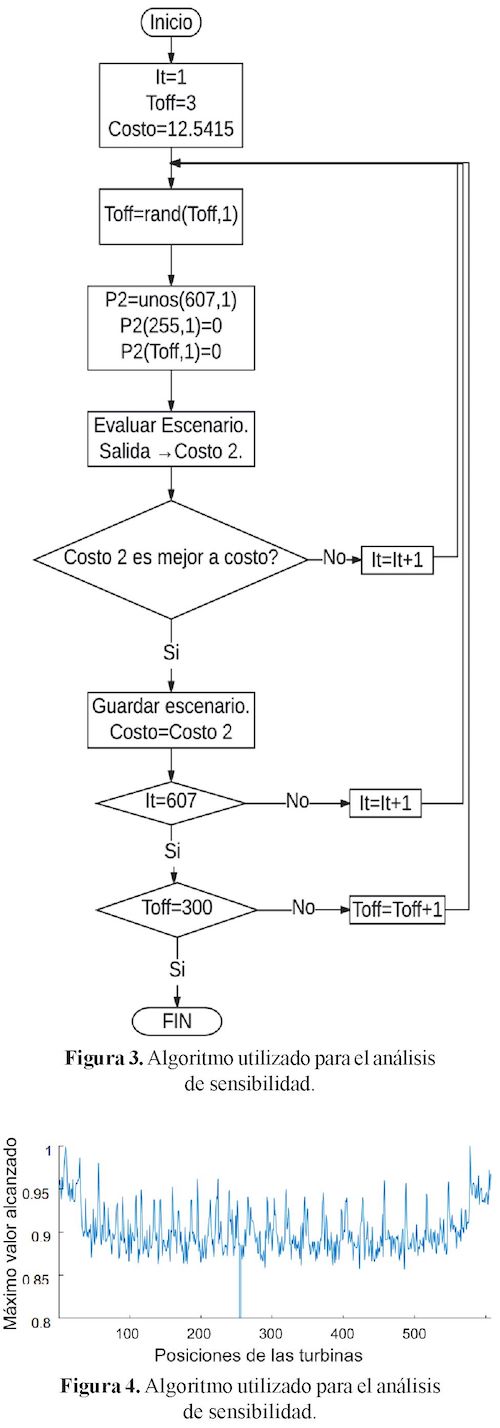
La máxima cantidad de turbinas instaladas se logró en la posición 578. En los 1674 escenarios estudiados, para esta posición se alcanzó un total de 1481 turbinas instaladas. La disrupción de la gráfica 4 en la posición 255 se debe a que, en todos los escenarios evaluados, esa posición nunca se consideraron turbinas instaladas.
De los 1674 escenarios obtenidos, se encontró que los mejores resultados de turbinas sin instalar se encontraban entre 2 y 250. Para resultados mayores a 250 turbinas sin instalar, el costo era mayor al costo mínimo considerado. La cantidad de veces que se repitió cada escenario se puede ver en la figura 5.
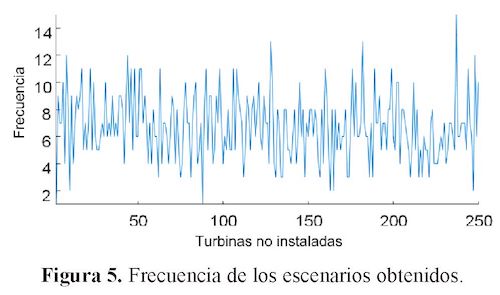
En la figura 5 se tiene en el eje horizontal el rango de turbinas en cero (turbinas sin instalar en esa posición), entre 2 y 250. En el otro eje se representa la frecuencia de cada escenario. El escenario que más se repitió (15 veces) se dio con 237 turbinas sin instalar en el layout.
Las figuras 4 y 5, muestran un comportamiento aleatorio en la distribución, no obstante, reduce el espacio de búsqueda de manera drástica debido a que los escenarios que tienen más de 250 turbinas sin instalar tienen un costo mayor al mínimo considerado.
En cuanto a los costos, de los 1674 escenarios, se obtuvieron resultados de mejor calidad con base en este método en contraste con los análisis realizados anteriormente. El menor costo fue de 12,3985. El mayor costo estuvo en 12,9648. Los costos se comparan en la figura 6.
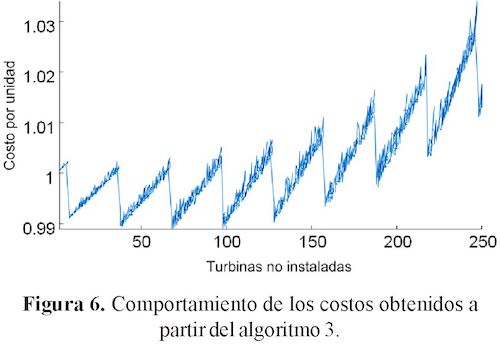
En la figura 6, el eje de las abscisas representa la totalidad de turbinas que no se consideran en el layout. En total, en este proceso se tuvo entre 2 y 250 turbinas. El eje de las ordenadas registra los costos de la energía, comparado con el costo obtenido por el escenario P1. Se puede notar que hay escenarios que lograron un costo mejor al que ya se había encontrado y, que a medida que se aumentaba la cantidad de turbinas sin instalar, el costo tenía una tendencia a aumentar.
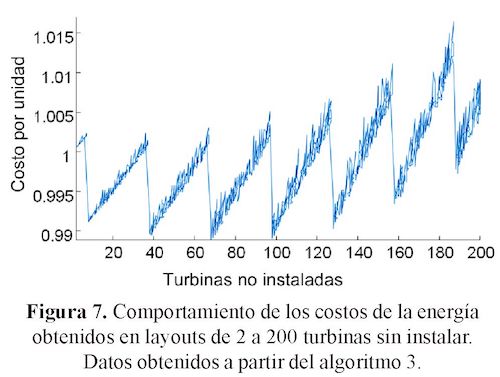
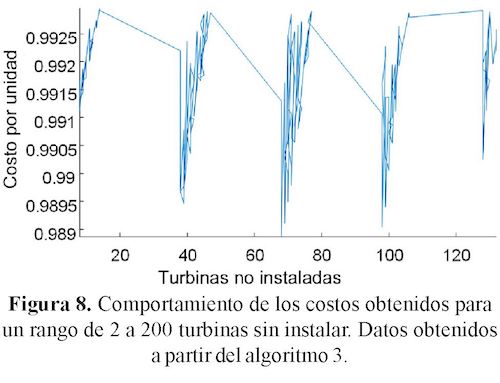
Se encontró que al no considerar en el layout entre 2 y 200 turbinas (figura 7) los resultados eran significativamente mejores a los encontrados anteriormente con los análisis de sensibilidad de los escenarios contemplados (P1 a P3). En la figura 8 se puede ver un comportamiento más claro del costo en por unidad, sin disponer en el layout de entre 2 y 160 turbinas. En todo este sub-espacio de búsqueda, los costos fueron menores al valor de comparación encontrado inicialmente.
Con los resultados obtenidos a partir del algoritmo propuesto en la figura 3, se quiso encontrar que subespacios se podían explotar más por medio de heurísticas y cuales se podían descartarse como espacios de búsqueda. De tal forma, se estableció el siguiente criterio, si el resultado es menor a 12,45, se almacenaba ese escenario para futuros análisis.
En este análisis de sensibilidad, se instaló un número aleatorio de turbinas, con un criterio de parada de 2000 iteraciones. En la figura 9 se muestra el comportamiento del costo de la energía en función del número de turbinas instaladas.
Se encontró que a medida que disminuye la cantidad de turbinas instaladas, los costos de la energía aumentan. Este comportamiento da una primera aproximación de cómo se distribuyen los costos.
Uno de los análisis propuestos consistió en utilizar una heurística denominada en [5] como cambio de posición. En esta heurística de bajo nivel, a partir de un escenario obtenido y almacenado, se desplaza cada uno de los datos una posición una vez a la derecha y se evalúa para determinar el costo de la energía. Este algoritmo se aprecia en la figura 10.
Se encontró, que al aplicar la heurística de cambio de posición se encuentran soluciones cercanas a la solución obtenida del espacio de búsqueda utilizado. Es decir, las respuestas obtenidas en un 80% eran de igual o peor calidad a la respuesta encontrada, mientras que el restante 20% están bastante cercanas a la solución inicial. Este análisis se deriva de la figura 11.

Los primeros 1500 cambios de posición están dentro del 80% de respuestas de igual o peor calidad, mientras que después de los 1500 cambios de posición ejecutados (el restante 20%), se tienen soluciones de una calidad levemente mejor.
El algoritmo propuesto aquí, que se denomina banco de posiciones, se basó en almacenar los mejores resultados obtenidos de las diferentes iteraciones. La idea subyacente es que alrededor de los mejores resultados, existen óptimos por explotar y que dada la complejidad del problema no es posible.
Por ejemplo, uno de los vectores obtenidos anteriormente (denominado de ahora en adelante el vector Q1) tiene la distribución que se muestra en la figura 12.
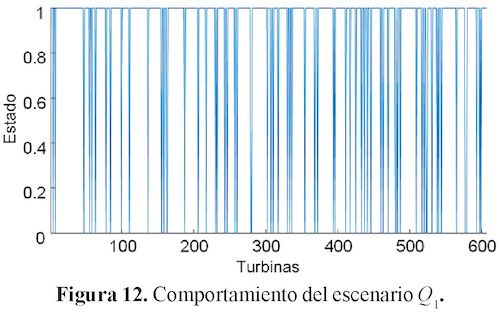
En la figura 12, se tiene en el eje horizontal todas las posibles posiciones (de 1 a 607), mientras que el eje vertical, establece el estado de cada posición: uno, si se instala una turbina en ese lugar y cero, si es lo contrario. Para este ejemplo en particular, Q1 cuenta con 537 turbinas instaladas.
De manera similar, se presenta en la figura 13 otro resultado que está dentro de la élite (menores a un costo de 12,45).
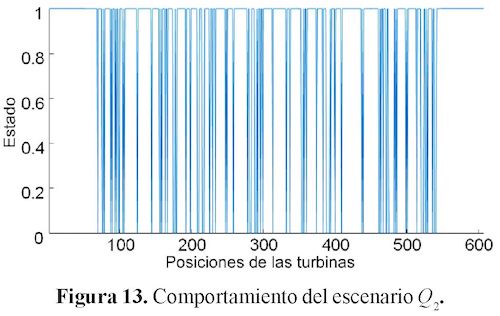
Con Q1 y Q2 almacenados, se configuró un algoritmo donde se cruzaban estos dos escenarios entre sí para determinar dos cosas: los lugares donde siempre había una turbina instalada y los lugares donde no (figura 14). Con esta segunda información, se creaba una matriz denominada banco de posiciones, donde posteriormente, se seleccionaba posiciones aleatorias de las posiciones encontradas y se evaluaban en la función de costos.
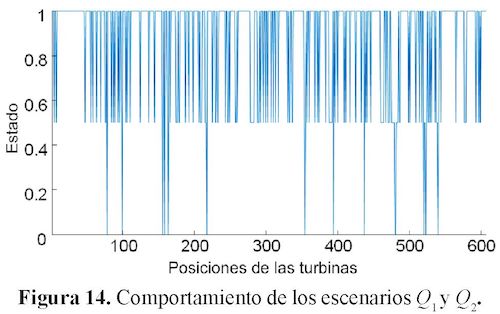
La figura 14 muestra en el eje de las ordenadas la probabilidad de encontrar una turbina instalada en ese lugar. En estos casos se contemplan únicamente dos escenarios, en consecuencia, se dan tres casos al mirar cualquier posición (xi, yi): encontrar una turbina en esa posición, cincuenta por ciento de probabilidad de encontrar una turbina o no encontrar una turbina instalada en esa posición.
Los resultados encontrados por medio del banco de posiciones, permitieron minimizar el problema ya que estos eran homogéneos y estaban dentro de la élite de resultados. Las figuras 15 y 16 permiten comprender mejor la evolución del banco de posiciones.
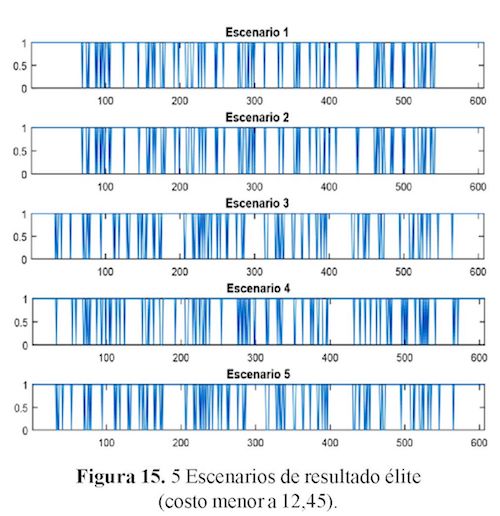
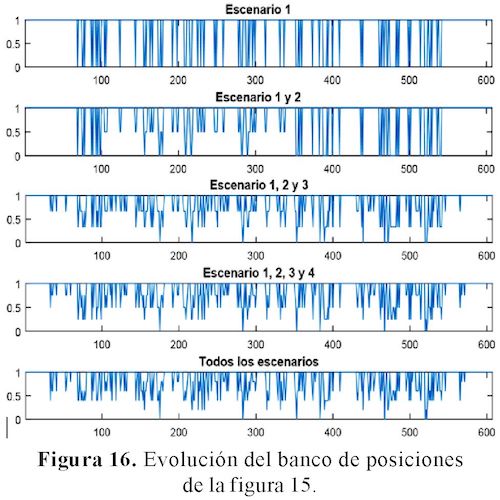
La metaheurística de alto nivel que se aplicó se denomina Binary Ant Lion Optimizer.
En el trabajo realizado en (Rivera & Gutiérrez, 2017) se realizó una evaluación del algoritmo BALO orientado al problema de optimización de diseños de parques eólicos. Se encontró que los resultados eran mejores a la repuesta obtenida mediante algoritmos genéticos. En la tabla 3 se muestra el resumen de los resultados presentados en (Rivera & Gutiérrez, 2017).
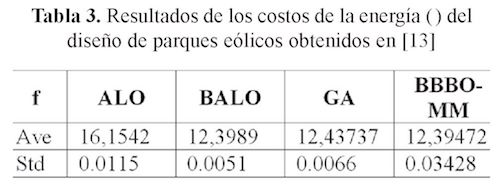
Al adicionar la heurística que obtuvo mejores resultados (banco de posiciones) al algoritmo de variables binarias basado en la caza de la hormiga León, se encontró una mejora significativa en el costo de la energía encontrado en 3. Al aplicar la metaheurística binaria se obtuvo un costo promedio de 12,39472, mientras que, en el presente trabajo, el costo promedio alcanzado fue de 12,3571 con una baja dispersión de los resultados obtenidos. En la tabla 4 se resumen los resultados.
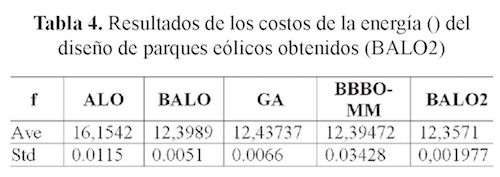
En el presente documento se realizó un resumen del uso de técnicas heurísticas y metahurísticas para el diseño de parques eólicos, planteándose como un problema de optimización del costo por medio del diseño de parques eólicos y los principales aportes obtenidos en cada una de las técnicas aplicadas al problema. Se presentó un marco teórico y conceptual que aborda el problema, encontrándose que resolver éste tipo de problemas por medio de metaheurísticas arroja resultados de mejor calidad que los obtenidos por medio de técnicas empíricas. En particular, se pudo evidenciar que el uso de algoritmos basados en el manejo de variables binarias (Binary Ant Lion Optimizer) permitió llegar a respuestas de mejor calidad. De igual forma, se encontró que al adicionar heurísticas de bajo nivel a técnicas metaheurísticas de alto nivel, se obtienen soluciones con mejor función objetivo. De esta manera con el presente artículo se sientan las bases para la profundización en la temática de optimización en el diseño de parques eólicos aplicando técnicas heurísticas y metaheurísticas, esta profundización se presenta en la tesis de pregrado de uno de los autores (Cantor, 2016).
Bilbao, M., Alba, E. 2009. Ga and pso applied to wind energy optimization. Master's thesis, Universidad Nacional de la Patagonia Austral, Universidad de Málaga.
Blum, C., 2005. Ant colony optimization: Introduction and recent trends. Physics of Life Reviews, 2(4):353-373. https://doi.org/10.1016/j.plrev.2005.10.001
Cantor, J., 2016. Optimización en el diseño de parques eólicos aplicando técnicas heurísticas y metaheu-rísticas. Dirigida por Sergio Rivera, tesis pregrado, Universidad Nacional de Colombia.
Coss, R., 1981. Análisis y evaluación de proyectos de inversión. Editorial Limusa, Lima.
Eroglu, Y., Ulusam, S., 2012. Design of wind farm layout using ant colony algorithm. Renewable Energies, 44:53-62. https://doi.org/10.1016/j.renene.2011.12.013
Gallego, R., Toro, E., Escobar, A., 2015. Técnicas Heurísticas y Metaheurísticas. Editorial UTP, Pereira, Colombia.
Gradya, S., Hussainia, Y., Abdullahb, M., 2004. Placement of wind turbines using genetic algorithms. Renewable Energies, 30(2):259-270.
IRENA., 2016. International renewable energy agency: Wind power technology brief.
Kennedy, J., Eberhart, R., 2009. Particle swarm optimization. Master's thesis, Universidad Nacional de la Patagonia Austral, Universidad de Málaga.
Kusiak, A., Song, Z., 2010. Design of wind farm layout for maximum wind energy capture. Renewable Energies, 35(3):685-694. https://doi.org/10.1016/j.renene.2009.08.019
Mirjalili, S., 2015. The ant lion optimizer. Advances in Engineering Software, 83:80-98. https://doi.org/10.1016/j.advengsoft.2015.01.010
Mirjalili, S., Mirjalili, S. M., Yang, X. S., 2014. Binary bat algorithm. Neural Computing and Applications, 25(3):663-681. https://doi.org/10.1007/s00521-013-1525-5
Mosetti, G., Poloni, C., Diviacco, B., 1994. Optimization of wind turbine positioning in large windfarms by means of a genetic algorithm. Wind Engineering and Industrial Aerodynamics, 51(1):105-116. https://doi.org/10.1016/0167-6105(94)90080-9
Rivera, S., Gutiérrez, J., 2017. Benchmark functions optimization using binary biogeography-based optimization with aleatory-mixed migration (bbbo-amm) and binary ant-lion optimizer (balo). under review.
Saavedra-Moreno, B., Salcedo-Sanz, S., Paniagua-Tineo, A., Prieto, L., Portilla-Figueras, A., 2011. Seeding evolutionary algorithms with heuristics for optimal wind turbines positioning in wind farms. Renewable Energies, 36(11):2838-2844. https://doi.org/10.1016/j.renene.2011.04.018
Samorani, M., 2013. Handbook of Wind Power Systems. The Wind Farm Layout Optimization Problem. Springer Verlag Berlin Heidelberg, New Delhi, India.
WFLO., 2015. Wind farm layout optimization competition. Consultado en 2015. https://www.irit.fr/windcompetition/2015/#home