Bifurcaciones en sistemas de redes neuronales

Bifurcations of neuronal networks systems

Mauro Montealegre Cárdenas¹, Jasmidt Vera Cuenca² y Edgar Montealegre Cárdenas³

Resumen

En este trabajo se exploran los conceptos de los sistemas dinámicos que explican las sinergias en las redes neuronales biológicas modeladas con la ecuación de Morris-Lecar, según se asume que las neuronas o grupos de neuronas sean osciladores, o no, en los niveles celular, sinapsis neuronal o conectividad de la red. Para los subsistemas para tiempo rápido se identifican las soluciones singulares y las soluciones “Burstings”. En este sistema dinámico de complejidad jerárquica los parámetros son las variables del subsistema lento. Para explicar inestabilidadades y transitoriedades se usa la teoría genérica de las bifurcaciones que caracteriza aspectos mesoscópicos de la conectividad de la red y filogénicos sobre los cambios típicos de comportamiento. Se extiende este estudio a modelos de redes neuronales artificiales recurrentes, en particular al modelo de Hopfield.

Palabras Claves: Redes Neuronales; soluciones singulares; soluciones “burstings”; ecuación de Morris-Lecar; modelo de Hopfield; Bifurcaciones; nivel mesoscópico; complejidad jerárquica

Abstract

This paper explores the concepts of dynamic systems that explain synergies in biological neural networks modeled with the Morris-Lecar equation, assuming that neurons or groups of neurons are oscillators, or not, at the cellular, neuronal synapses or network connectivity. For the fast-time subsystems, unique solutions and "Burstings" solutions are identified. In this dynamic system of hierarchical complexity, the parameters are the variables of the slow subsystem. In order to explain instability and transience, the generic bifurcation theory that characterizes mesoscopic aspects of network and phylogenetic connectivity over typical behavioral changes is used. This study is extended to models of recurrent artificial neural networks, in particular to the Hopfield model.

Keywords: Neural networks; singular solutions; "burstings" solutions; Morris-Lecar equation; Hopfield model; Bifurcations; mesoscopic level; hierarchical complexity.

1. Introducción

A partir de los resultados recientes sobre la Matemática Neuronal, se ha realizado un estudio de las sinergias en las redes neuronales resaltando la emergencia de la complejidad por mecanismos de auto-organización en circunstancias cambiantes, explicada estructural y funcionalmente a partir de las interacciones entre las variables de estado dependientes de los pesos sinápticos; se ha estudiado también sus características filogénicas descritas en el espacio de parámetros que se formalizan en sus bifurcaciones genéricas, también llamados factores de inestabilidad y transitoriedad.

Este artículo se refiere a las ecuaciones de Morris-Lacar (Bard Ermentrout & Terman, 2012) que involucra un sistema dinámico en tres dimensiones, con un único equilibrio auto-conectado mediante una órbita homoclínica con una variedad estable unidimensional y una variedad inestable de dos dimensiones, cuya dinámica es propuesta en (Montealegre, Montealegre Cardenas, Vera cuenca , & Montealegre Cardenas, 2015).

Se destaca que las neuronas individualmente exhiben patrones de disparo más complejas que las descargas repetidas, son las oscilaciones explosivas también denominados “Burstings”, que se caracterizan por una fase de silencio alternada con una fase activa de oscilaciones rápidas, para ello se requieren al menos dos mecanismos biofísicos: un mecanismo responsable de la generación de adición y un mecanismo de modulación lenta, que se modelan como perturbaciones singulares (Izhikevich, 2007), dependiendo de múltiples escalas de tiempo.

Se relaciona con detalles los niveles jerárquicos de los sistemas dinámicos correspondientes a las redes neuronales en los niveles de: propiedades intrínsecas de células en la red, propiedades sinápticas de conexión entre neuronas y la topología de la conectividad en la red. Las dos primeras tienen múltiples escalas de tiempo y la dinámica celular depende de las variables de disparo en los canales. Una célula puede tener variedad de patrones de encendido: disparos repentinos, estallido de oscilaciones y dinámica caótica. Las sinapsis globales que pueden ser excitatorias o inhibitorias determinan cómo una célula, o grupos de células, influyen en las otras, lo cual se denomina la plasticidad del sistema. Las diferentes clases de arquitectura neuronal hacen que la conectividad sea esparcida o densa, aleatoria o altamente estructurada.

También se tratan aspectos interdisciplinarios de la dinámica del aprendizaje de las redes neuronales artificiales, como es el caso del modelo neuronal de Hopfield (Hopfield, 1984) que modelan las máquinas de Boltzmann descritas (Siri, 2007) y en (Bard Ermentrout & Terman, 2012).

2. Dinámica Unicelular

2.1. Ecuación del potencial de acción

La relación entre la carga almacenada y el potencial es 𝑞=𝐶_𝑀𝑉_𝑀 , con una constante de proporcionalidad 𝐶_𝑀 llama la específica, . Si 𝑔̂_𝐾 es la conductancia de un solo canal de 𝐾⁺ y la corriente iónica a través de este canal es 𝐼̂_𝐾=𝑔̂_𝐾(𝑉_𝑀−𝐸_𝐾). Aquí 𝐸_𝐾 es el potencial de Nernst 𝐾⁺. La fuerza impulsora es 𝑉_𝑀−𝐸_𝐾 y 𝐼_𝐾=𝑔_𝐾(𝑉_𝑀−𝐸_𝐾)=. La ley de Kirchhoff conduce a la siguiente ecuación diferencial (1) sobre el potencial de membrana:

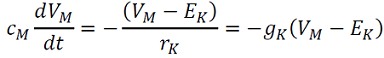. (1)

Este potencial depende de la variable espacio-temporal y con corrientes óhmicas debidas a los canales abiertos para 𝐾⁺ ,𝑁𝑎⁺ y 𝐶𝐿⁻, entonces la corriente de fuga 𝐼_𝐿 es dada por −𝐼_long(𝑥+Δ𝑥,𝑡)+𝐼_long(𝑥,𝑡), con 𝐼_𝐿=𝐼_cap+𝐼_ion . Esto produce la siguiente ecuación (2) del potencial de acción,

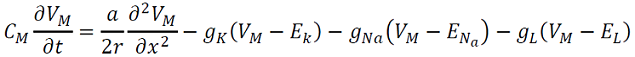. (2)

2.3 Modelo de Morris-Lecar y Bifurcaciones

El sistema de Morris-Lecar (3) descrito en (Izhikevich, 2007) despliega alta complejidad dinámica a partir de las siguientes ecuaciones,

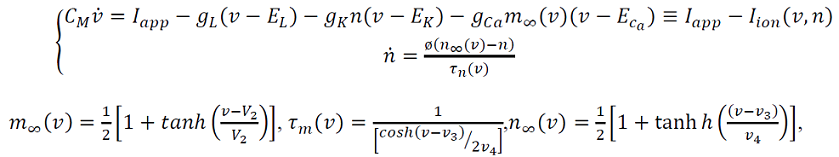(3)

donde 𝑣1,𝑣2,𝑣3 𝑦 𝑣4 son los parámetros de voltaje. Este modelo genera los siguientes cambios de comportamiento o bifurcaciones (Geovearts, 2013) y (Kuznetsov, 2004):

a. Las bifurcaciones de Takens-Bogdanov descrita en (Hastings, 1976) que tiene la siguiente forma normal.

1. 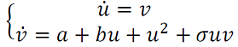, si 𝜎<0 es supercrítico.

b. Bifurcaciones homoclínicas del tipo silla para una órbita crítica en 𝐼_𝑎𝑝𝑝=𝐼_𝐻𝑐 con periodo . La forma normal para este tipo de bifurcaciones homoclínico depende de la cantidad 𝜆₁+𝜆₂ en el punto de silla y es (𝜆₁+𝜆₂<0 en el supercrítico.

El sistema Morris-Lecar también exhibe patrones complejos denominadas oscilaciones explosivas, “bursting oscilations” (Bard Ermentrout & Terman, 2012) que involucra perturbaciones singulares para 𝜀 > 0, parámetro singular pequeño. Las soluciones “burstings” generalmente comienzan o terminan en puntos homoclínicos. Como ejemplos de “bursting” tenemos:

a. “Bursting” de cuadratura de onda.

El modelo Morris-Lecar relacionando con una tercera ecuación singular genera un régimen homoclínico con parámetro 𝐼_𝑎𝑝𝑝, 𝐼_𝑎𝑝𝑝=𝐼_𝐻𝑜𝑚 ó 𝐼_𝑎𝑝𝑝=𝐼_𝑆𝑁 y tiene un comportamiento biestable de (4) denominado histérisis, se expresa mediante el siguiente sistema:

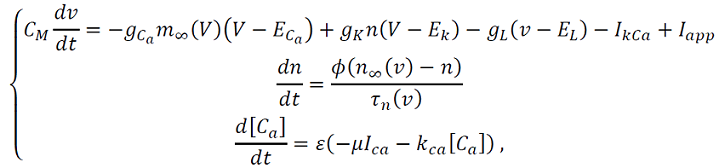(4)

La corriente de calcio dependiente del potasio es 𝐼_𝑘𝑐𝑎=𝑔_𝑘𝑐𝑎𝑧(𝑣−𝐸_𝑘), 𝑔_𝑘𝑐𝑎 es la conductancia máxima para esta corriente y 𝑧 es la variable de compuerta que relaciona la concentración de calcio [𝐶_𝑎] en la membrana. Observamos comportamiento caótico en 𝜆=𝑘_𝑐𝑎. Este “Bursting” es ilustrado en la figura 1.

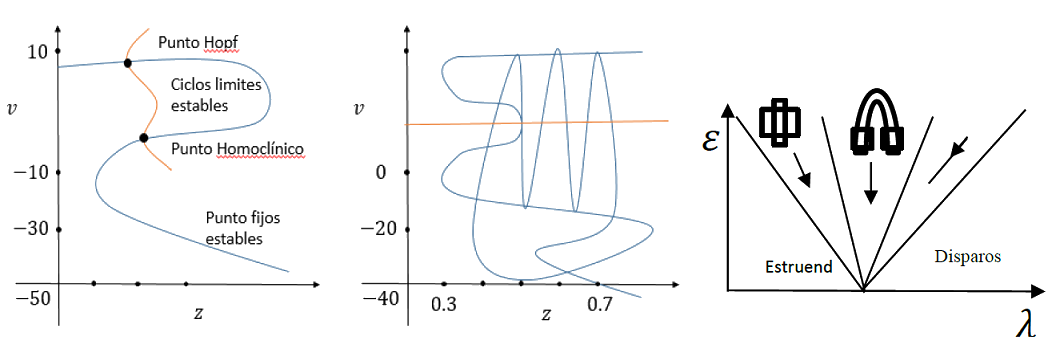
Figura 1. Bifurcaciones del tipo “Square Wave Bursting” puede generar caos (Montealegre Cardenas , Londoño Betancourth, & Polania Quiza, 2012)

b. “Bursting” parabólico.

Si a los modelos los relacionamos con 𝐼_𝐶𝑎𝑆=𝑔_𝐶𝑎𝑆𝑆(𝑣−𝐸_𝐶𝑎), la cual depende de la variable 𝑠 y 𝑠_∞(𝑉)=, obtenemos el siguiente sistema 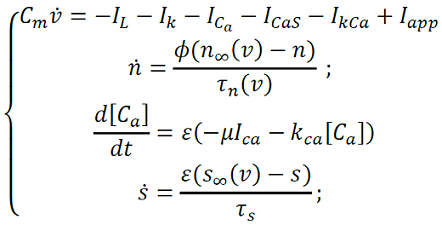(5),

(5)

Que cual tiene 2 variables rápidas, 𝑉 𝑦 𝑛, 2 variables lentas [𝐶_𝑎] 𝑦 𝑠 . Usando esta descomposición sistema rápido/lento estudiamos primero la dinámica lenta mediante el siguiente cambio de variables 𝜏 = 𝜖𝑡, que sustituimos el siguiente sistema generalizado,

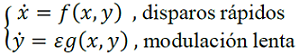
donde 𝑥 ∈ ℝ^𝑚 ,𝑦 ∈ ℝ² . En 𝜀 = 0 obtenemos el siguiente sistema 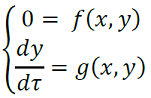(6),

(6)

Observemos que la primera ecuación dice que durante la fase de silencio la solución singular está por debajo de la superficie de puntos fijos. Se soluciona la primera ecuación como 𝑥 = 𝑥_rest(𝑦) y se reemplaza en la segunda para obtener 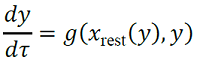(7),

(7)

este es el subsistema reducido para estudiar la dinámica lenta hasta la fase de silencio.

Asumiendo que 𝑦 = (𝑦₁,𝑦₂) está en la región donde existe ciclos límites estables del sistema rápido, hacemos 𝑥_𝑝𝑒𝑟(𝑡) una solución periódica con período 𝑇(𝑦), y consideramos el siguiente sistema promedio 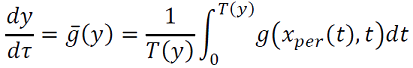(8),

(8)

considerando las dos variables lentas 𝑦₁ y 𝑦₂ como parámetros, haciendo una de las variables lentas como constante. El diagrama de bifurcación resulta una curva de puntos fijos y una curva de órbitas periódicas que se originan en un punto de Hopf sub-crítico y la transición al caso supercrítico, denominada bifurcación de co-dimensión 2 del tipo Bautin (Kuznetsov, 2004).

3. Dinámica Multineuronal

3.1. Acoplamiento físico, oscilaciones neuronales

De (Brown, Mahetius, & Holmes, 2004) tenemos en ℝ^𝑛 la ecuación diferencial con una solución periódica 𝑋(𝑡) de periodo 𝑇 , orbital y asintóticamente estable, representada como Γ y parametrizado con la fase, ɵ ∈ [0,𝑇), que llamamos Θ(𝑥), para cada 𝑥 ∈ Γ.

Si Γ es asintóticamente estable, se define la fase de 𝑦, puntos en una vecindad de Γ, entonces Θ(𝑥) = Θ(𝑦), pues si x∈ Γ, entonces ‖𝑋(𝑡;𝑥) − 𝑋(𝑡,𝑦)‖ →0 cuando 𝑡 → ∞, esto es decir estas soluciones son indistinguibles.

El conjunto de 𝑦 que tiene la misma fase asintótica es llamado el isócrono de Γ, conjunto denotado como 𝑁(𝒙), conjunto que resulta ser invariante, esto es, si 𝑦 ∈ 𝑁(𝒙),𝑋(𝑇,𝑦) ≡ 𝑦' ∈ 𝑁(𝒙), 𝑦 → 𝑦' es mapeo de Poincaré para Γ sobre la sección transversal 𝑁(𝒙), la cual toma exactamente un tiempo 𝑇.

Una pequeña perturbación para el campo de vectores con fase 𝜙 lo lleva a la nueva fase 𝜙' , generado la Curva de Transición de Fases (CTF), 𝜙' = 𝑷(𝜙), una función inyectiva del intervalo [0,𝑇) en sí mismo. Para las perturbaciones la Curva de Reacomodación de Fases (CRF) es la diferencia entre la nueva y antigua fases,

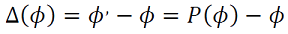(9)

La curva CRF está relacionada con 𝑇' y satisface . Si 𝑇′ < 𝑇 entonces el estímulo hace avanzar la fase. Relacionamos la curva CRF con la función Θ(𝑥), 𝑥 = 𝑋₀(𝜙) ∈ Γ, Γ parametrizado en 𝑋₀(𝑡) con la fase 𝜙 ∈ [0,𝑇), esto es, Θ(𝑥) = 𝜙.

Una perturbación del campo 𝑦 ∈ ℝ^𝑛 produce 𝜙′ = 𝜙(𝑥+𝑦) = 𝜙 + ∇_𝑥Θ(x).y + O(|𝑦|²), esto significa que Δ(𝜙:𝑦) = ∇_𝑥Θ(x). Si 𝑦 = (𝑎,0,…,0) entonces CRF es la primera componente del gradiente de la función de fase Θ(𝑥) evaluada en 𝑋₀(𝜙) y la notamos como 𝑍(𝜙) = ∇_𝑥Θ(X₀(𝜙)).

Sea 𝑋₀(𝑡) una solución límite T-periódica y la matriz 𝑛 × 𝑛 𝐴(𝑡) = 𝐷_𝑥𝐹(𝑥)|_𝑥0(𝑡), entonces la solución del sistema lineal resuelve el siguiente operador 𝐿 (10),

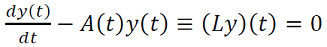, (10)

Su adjunto es satisface este último operador.

Si 𝑋₀(𝑡) es un ciclo límite estable, el espacio nulo de 𝐿 es generado por un múltiplo escalar de y el espacio nulo de 𝐿^∗ en el espacio de la funciones 𝑇 − periódicas en ℝ^𝑛 múltiplos de 𝑍(𝑡), que satisface Θ(X₀(𝜙)) = 𝜙 y por ello , es 𝐿∗𝑍 = 0. Para estudiar la estabilidad de la solución, hacemos 𝐿∗(𝑦) = 0 que se resuelve integrando para tiempos negativos, la ecuación . En coordenadas de faces 𝜙 ∈ [0, T), para una cantidad 𝑇_𝑓 , obtenemos 𝑀 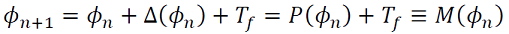(11),

(11)

donde 𝑃(𝜙) es el mapeo de transición de fase (PTC); 𝑃′(𝜙) = 1 + Δ′(𝜙). En lugar de considerar 𝜙𝑛 con respecto a T, la dejamos evolucionar en la recta real definiendo la rotación (12) de la siguiente manera,

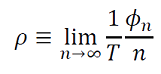(12)

Resultando que si en promedio 𝜌 = 1, el oscilador completa un ciclo por estímulo, es 1:1. Si 𝜌 = 2/3, entonces el oscilador completa dos ciclos para cada tres de los estímulos, 2:3. Estas soluciones resonantes resuelven el siguiente Teorema de Denjoy:

Teorema. “El número de rotación está bien definido; es decir, el límite existe y es independiente de la condición inicial. Por otra parte, si 𝑀(𝜙) es dos veces continuamente diferenciable, entonces:
1. 𝜌 es racional si y sólo si 𝑀(𝜙) tiene una órbita periódica de un período: 𝜙_𝑛+𝑁 = 𝜙_𝑛mod 𝑇.
2. 𝜌 es irracional si y sólo si cada órbita {𝜙_𝑛} es densa en el círculo.
3. 𝜌 es una función continua de los parámetros en la función 𝑀.”

3.2. Plasticidad

Corresponde al proceso hace que el cerebro desarrolle nuevas habilidades a lo largo de la vida (Erdi, 2010) estimulando aprendizaje no trivial. La plasticidad se define usando la concentración [𝑇] de transmisores liberados en la hendidura sináptica para un pico presináptico. La plasticidad 𝑠 (𝑡), que es la fracción de canales abiertos, satisface la siguiente ecuación probabilística (13):

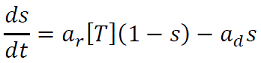. (13)

Si 𝑡 = 𝑡₀, [𝑇] salta a [𝑇_𝑚𝑎𝑥 ] en 𝑡 = 𝑡₁, [𝑇] cae de nuevo a 0. Entonces

𝑠(𝑡 − 𝑡₀) = 𝑠_∞ + (𝑠(𝑡₀) − 𝑠_∞)𝑒^{−(𝑡−𝑡0)/𝜏𝑠}, 𝑡_{0 < 𝑡 < 𝑡1, 𝑠∞ = y ; 𝑠 (𝑡) decae hacia 𝑠(𝑡) = 𝑠(𝑡1)𝑒^{−𝑎𝑑(𝑡−𝑡1)} hasta obtener 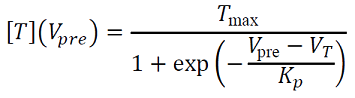(14),}

(14)

La corriente para este tipo de sinapsis es 𝐼_gap = 𝑔̅_gap(𝑉_post − 𝑉_pre) donde 𝑔̅_gap es la conductancia.

En general la plasticidad puede producirse en una actividad que puede expresarse mediante el siguiente sistema 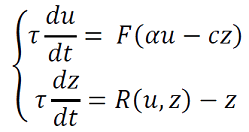(15),

(15)

𝜏_𝑧 >> 𝜏,𝐹 es el potencial de acción y 𝑅(𝑢,𝑧) es la adaptación por excitación que no excede 1. Un modelo más realista es 𝑅(𝑢,𝑧) = 𝛼𝐹 con 𝑅(𝑢,𝑧) = 𝛼𝐹(1−𝑧).

En las siguientes secciones de la 3.3) a la 3.6) de este trabajo seguimos a (Ermentrout & Terman, 2012), dado que este autor usa con apropiadamente el paradigma ondulatorio para describir la complejidad de los procesos de aprendizajes sinápticos (excitatorio o inhibitorio).

3.3. Acoplamiento químico: sinapsis excitatoria o inhibitoria.

Arquitectura de una red neuronal puede ser global o local, densa o espaciada, aleatoria o determinística, en general se modela una red neuronal que se puede representar con grafos, acoplada fuertemente según el siguiente sistema 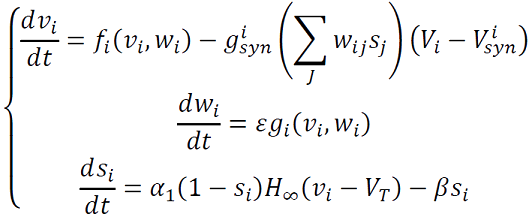(16):

(16)

donde 𝑖 , 𝑗 son 1 o 2 con 𝑖≠𝑗. Asumimos que las células son heterogéneas en el sentido de que las funciones no-lineales 𝑓_𝑖 y 𝑔_𝑖 dependen de 𝑖 ; algunas células son excitatorias y otras inhibitorias; los pesos sinápticos 𝑊_𝑖𝑗 son las probabilidades de que la célula 𝑖 se conecte con la célula 𝑗. Asumimos que las células están en un dominio 𝐷 y 𝑣(𝑥,𝑡) el potencial de membrana en la posición 𝑥 en el tiempo 𝑡.

Después de un reescalonamiento apropiado el sistema anterior se puede expresar como (17) así:

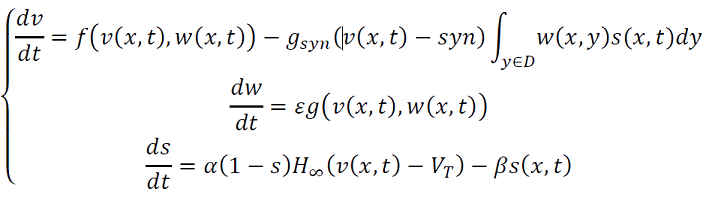(17)

Hacemos 𝜙(𝑣,𝑤,𝑠) = 𝑓(𝑣,𝑤)−𝑔_𝑠𝑒𝑔𝑠(𝑣−𝑣_𝑠𝑦𝑛), así si 𝑔_𝑠𝑦𝑛 es acotado, cada 𝐶_𝑆 = {𝜙(𝑣,𝑤,𝑠) = 0} es una curva que tiene forma cúbica, para las cuales expresamos el lado izquierdo de 𝐶_𝑆 como {𝑣 = 𝜙_𝐿(𝑣,𝑤,𝑠)} y su derecho como {𝑣 = 𝜙_𝑅(𝑣,𝑤,𝑠)}. Donde 𝐻_∞ es una función de escalón unitario, función de Heaviside, 𝐻_∞(𝑣) = 0 si 𝑣 < 0 y 𝐻_∞(𝑣) = 1 si 𝑣 > 0.

3.4. Propagación de ondas

Ahora estudiamos el patrón de propagación de ondas considerando dos capas de neuronas, una excitatoria y una inhibitoria. Para ello suponemos que la interacción de cada capa es modelada mediante el siguiente sistema 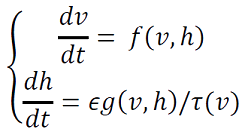(18),

(18)

La 𝑣-isoclina tiene forma cúbica "al revés", porque la variable lenta ℎ representa la disponibilidad de la T-corriente interna, en lugar activación de la corriente de potasio. Si una célula recibe la entrada inhibitoria, entonces esto eleva la 𝑣-isoclina y la célula se mueve hacia el nuevo equilibrio, la curva 𝑣-isoclina vuelve a la posición original (𝑠 = 0), queda (𝑣,ℎ) por encima de ℎ_𝑚𝑎𝑥. (Ermentrout & Terman, 2012) y corresponde a una onda denominada “indecisa”.

3.5. Ontogenia: Frente de ondas

La excitación recurrente hace que las neuronas vuelvan a disparar después de los disparos de las células vecinas, por ello la corriente sináptica está dada por la siguiente integral 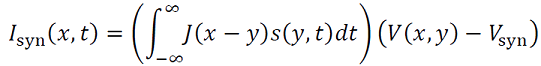(19),

(19)

donde 𝐽 describe las fuerzas de las interacciones dependientes de la distancia y 𝑠(𝑥,𝑡) satisface (20) una ecuación diferencial de la forma

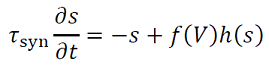(20)

la función 𝑓(𝑉) es cero, a menos que el voltaje este por encima de cierto umbral, ℎ(𝑠)=1−𝑠 o ℎ(𝑠)=1.

3.6. Filogenia: Generación sináptica de pulsos.

Para convertir el frente de ondas en pulsos (21) se inyecta gradualmente corrientes negativas, lo que se consigue adicionando dos corrientes lentas: la excitación sináptica y la adaptación,

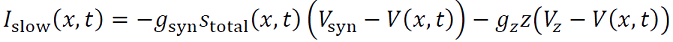(21)

donde la corriente sináptica (22) satisface el siguiente sistema,

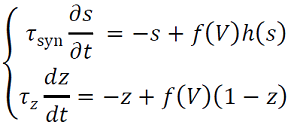(22)

𝑓_𝑧(𝑉) es cero a menos que la neurona se despolariza suficientemente y 𝜏_𝑧 es la constante de recuperación lenta. La corriente total en una célula es dada por 𝐼_slow(𝑥,𝑡) ≈ 𝐼_rev𝑠_total(𝑥,𝑡 )+𝐼_𝑧𝑧(𝑥,𝑡), donde 𝐼_rev=𝑔_syn(𝑉_rest− 𝑉_syn) > 0, 𝐼_𝑧=𝑔_𝑧(𝑉_rest−𝑉_𝑧) < 0, 𝑠_total es la entrada total en 𝑥 de otras células, la red es el siguiente sistema 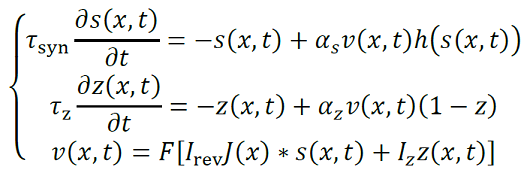(23),

(23)

Se puede asumir que 𝜖 = 𝜏_syn/𝜏_𝑧 ≪ 1 con 𝜏_syn = 1 con una solución de pulso,(𝑠 (𝑥,𝑡),𝑧 (𝑥.𝑡)) = (𝑆(𝜉),𝑍(𝜉)), dónde 𝜉=𝑥−𝑐𝑡 y 𝑐 es la velocidad de la onda viajera.

4. Redes neuronales artificiales

De (Bard Ermentrout & Terman, 2012) y (Cohen-Grossberg, 1983) relacionamos un modelo para la conectividad de las redes neuronales basado en la densidad de disparos del sistema, 𝑢_𝑖, dependiendo no-linealmente del potencial somático, 𝑉_𝑖(𝑡), 𝑢_𝑖=𝐹_𝑖(𝑉_𝑖(𝑡)) donde 𝐹 la función logística. Asumimos un modelo de red neuronal recurrente con parámetros 𝜷 , la entrada y 𝜶, la fuerza de las conexiones, con y 𝐹′(𝑢) > 0. (Figura 2)

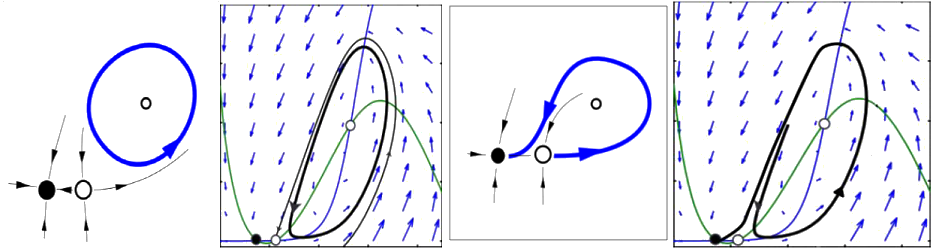
Figura 2. Bifurcación homoclínica con equilibrio Silla-nodo puede generar ciclos inestables (Montealegre Cardenas , Londoño Betancourth, & Polania Quiza, 2012).

La función 𝐹 tiene un único punto de inflexión y puede surgir una bifurcación silla-nodo en conexión homoclínica, como se ilustra en la FIG 2, porque la derivada del sistema lineal es

.

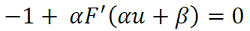Si 𝜶 es grande, como 𝐹 es invertible podemos resolver para 𝜷. Un modelo con 2 poblaciones de neuronas se obtiene el siguiente sistema 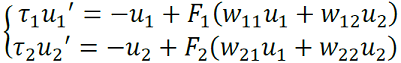(24),

(24)

Si 𝐹′_𝑗(𝑢) > 0 y 𝑤₁₂𝑤₂₁ > 0, la función más usada es .

4.1. Redes no estructuradas

Las dinámicas de estas redes son modeladas en (Cohen-Grossberg, 1983), según se refieran a tasa de disparos, la primera (25), o de potencial de acción (26), la segunda:

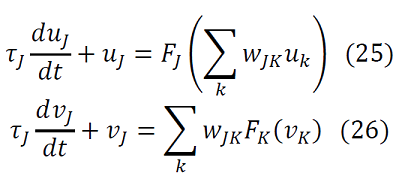
4.1 Modelos para redes determinísticas de Hopfiel.

En (Erdi, 2010) se describe la actividad de un sistema neuronal recurrente que corresponde, primero a la dinámica de aprendizajes de D. Hebb, el segundo es morfológico y es la dinámica intermodal con entradas 𝑦_𝑖 y salidas dadas por el siguiente sistema 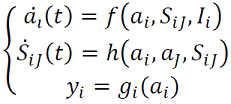(27),

(27)

Las interacciones entre las neuronas 𝑖 → 𝑗 se actualizan de acuerdo siguientes opciones (28), según los niveles de complejidad:

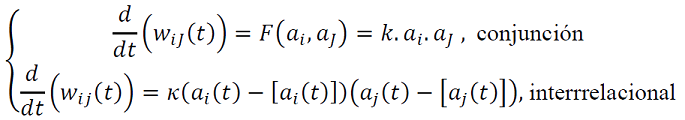(28)

Estos aprendizajes se inspiran en razonamientos: (Venturelli, 2015): deductivos, encontrando el efecto a partir de la causa y la regla; abducción, encontrar las causas con la regla y el efecto; Inducción, encontrar la regla con la causa y efecto; hipótesis heurística, referente a la solución a los problemas en estructuras simbólicas.

Si suponemos que el umbral para el error permanece constante, la actividad neuronal se puede resumir en siguiente modelo en tiempo continuo de Hopfield 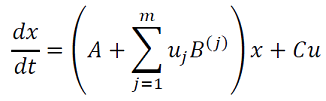(29),

(29)

donde (𝑥(𝑡)) describe los estados, conectividad sináptica consignada en: aprendizaje que se registra en la matriz A; el vector de parámetros es (𝑦 = (𝑦_𝑖)); la modulación de la conectividad 𝐵^(𝑗) y los parámetros de entrada el vector 𝐶. En resumen se obtiene en 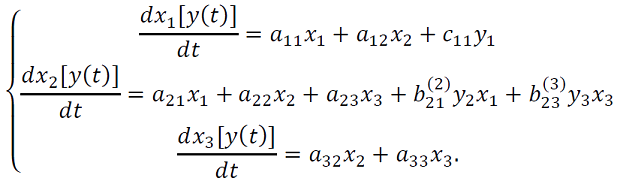(30),

(30)

4.4. Redes estocásticas recurrentes de Hopfield.

Si la función 𝐹: ℝ^𝑁 → ℝ^𝑁 tal que 𝐹_𝑖(𝑋) = 𝑓(𝑥_𝑖) con 𝑓(𝑥) = (1+tanh(𝑔𝑥)/2) y 𝑤^(𝑇) = la matriz de cargas sinápticas en la 𝑇-ésima época de aprendizaje, cuya dinámica (31) es,

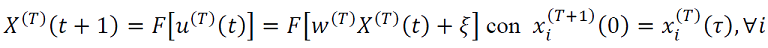(31)

𝑢^(𝑇)(𝑡) es el “potencial sináptico”, es el "patrón" a ser aprendido. La matriz de peso inicial 𝑤^(𝑇) se muestrea aleatoriamente e independientemente con una ley gaussiana con media 0 y varianza 1/𝑁; la matriz de cargas sinápticas 𝑤^(𝑇) contiene elementos positivos (excitación), negativos (inhibición) o nulos (sin sinapsis) y es asimétrica . La red puede mostrar diferentes regímenes dinámicos: Caos, (cuasi-) periodicidad, puntos fijos.

Definimos la siguiente formulación genérica para las reglas de aprendizaje de Hebb (Siri, 2007) dada por 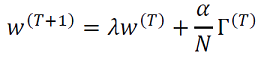(32),

(32)

Γ^(𝑇) es función ℎ es Hebbiana, ; 𝜆 ∈ [0,1] es la tasa de olvido, si 𝜆 < 1 y Γ_𝑖𝑗 = 0 (las neuronas pre- y post-sinápticas son silenciosas), una tasa característica es y no hay olvido cuando 𝜆 = 1, este valor de parámetro corresponde a una bifurcación silla-nodo de este sistema discreto.

5. Conclusiones

En este trabajo sobre sistemas de redes neuronales biológicas con herramientas neuro-matemáticas, se agregó un estudio de sinérgias a través de los factores de inestabilidad y transitoriedad, descritos con los métodos de la teoría de bifurcaciones.

De las interacciones entre sus subsistemas de tiempos rápidos o lentos, resultó una complejidad jerárquica y auto-organizada, que en circunstancias cambiantes corresponden, a nivel meso, la dinámica de grupos de neuronas especializadas. Estas descripciones geométricas surgen en estas redes y han sido modeladas a través de las formas normales de sus bifurcaciones.

Lo anterior permite establecer analogías entre las redes neuronales biológicas, operando con sus conexiones sinápticas, con las dinámicas generadas por modelos recurrentes de redes neuronales artificiales, en particular con los modelos de Hopfiel operando con las reglas del aprendizaje de Hebb. Este isomorfismo facilita conocimiento de la complejidad de los procesos cognoscitivos.

6. Referencias biliográficas

Bard Ermentrout, G., & Terman, D. H. (2012). Mathematical Fundations of Neuroscience. New York: Springer.

Brown, E., Mahetius, J., & Holmes, P. (2004). On the phase reductions an response dynamics of Neural oscillators populations. Neural Computing 16, 673-715.

Cohen-Grossberg. (1983). Absoluty stability global pattern formation and parallel memory storage by competitive (Vols. SMC-13).

Erdi, P. (2010). Complexity Explained. Springer.

Ermentrout, G., & Terman, D. (2012). Mathematical Fundations of Neuroscience. New York: Springer.

Geovearts, B. H. (2013). MatCont tutorial on starting up homoclinic orbits. California University .

Hastings, S. P. (1976). On the existence of homoclinic and periodic orbits for the FitzHung Nagumo equations. Quart J. Math 27, 123-154.

Hopfield, J. (1984). Neurons of graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci U S A, 18, 3088-3092.

Izhikevich, E. M. (2007). Systems in Neuroscience: Geometry of excitability and Bursting. Cambridge: MIT Cambridge.

Kuznetsov, Y. A. (2004). Elements of applied Bifurcations Theory. New York: Springer.

Montealegre Cardenas , M., Londoño Betancourth, G., & Polania Quiza, L. A. (2012). Fundamentos de los Sistemas Dinámicos. Neiva: Universidad Surcolombiana.

Montealegre, Montealegre Cardenas, M., Vera cuenca , J., & Montealegre Cardenas, E. (2015). Interacciones significativas entre los sistemas dinámicos del modelo de oscilaciones neuronales de Morris-Lecar y sistemas dinámicos de redes neuronales artificiales. Neiva: Proyecto Universidad Surcolombiana.

Siri, B. a. (2007). A matthematical analysis of the effects of Hebbien Learning rules on the dynamics and structure of discrete-time random recurrent neural network. Nice: Institut Non Linéaire de Nice.

Venturelli, A. (2015). Consideraciones Epistemológicas alrededor de las neurociencias cognitivas. Ciencias y cognición, 20(1), 018-28.

¹ Grupo de Investigación Dinusco, Universidad Surcolombiana
² Grupo Investigación Dinusco, Universidad Surcolombiana
² Grupo de Investigación Dinusco, Universidad Surcolombiana.