Rev. Ingeniería y Región, Vol. 19
Propuesta de un modelo de volatilidad a los precios de cierre en las acciones CÉMEX LATAM HOLDINGS durante el periodo 15/noviembre/2012 al 27/octubre/2017
Proposal of a volatility model to the closing prices in the CÉMEX LATAM HOLDINGS actions during the period 15/noviembre/2012 to 27/october/2017
Christian Camilo Cortes Garcia1 * y Alvaro Javier Cangrejo Esquivel2
Resumen
En este trabajo se presenta un modelo de volatilidad que explique los retornos de precios de cierre diarios de las acciones CLH de la compañía multinacional para la industria de la construcción CEMEX, al tomar como referencia la volatilidad con ventana móvil 20 datos y modelos de volatilidad condicional tales como los GARCH, TGARCH, IGARCH, EGARCH y APARCH. El modelo que mejor explica la volatilidad de los retornos es el IGARCH (1,1).
Palabras clave: Volatilidad condicional; volatilidad histórica ; función de autocorrelación; retornos diarios; distribución GED; criterios de información bayesiano.
Abstract
This paper presents a volatility model that explains the returns of daily closing prices of the CLH shares of the multinational company for the construction industry CEMEX, taking as reference the volatility with mobile window 20 data and conditional volatility models such such as GARCH, TGARCH, IGARCH, EGARCH and APARCH. The model that best explains the volatility of the returns is the IGARCH (1,1).
Keywords: Conditional volatility; historical volatility; autocorrelation function; daily returns; GED distribution; Bayesian information criteria.
1. Introducción
Por lo general, las series temporales de alta frecuencia que se observan en los mercados financieros no siguen una distribución normal, caracterizándose principalmente por ser asimétricas, leptocúrticas, elevada persistenciaen la volatilidad, correlaciones en los retornos al cuadrado, entre otros. De igual forma, una medida importante en las finanzas es el riesgo asociado con un activo y la volatilidad es una medida de incertidumbre, objeto de estudio por los inversionistas al momento de invertir.
Algunas investigaciones suponen que la varianza es determinista o constante a lo largo del tiempo, fijando como estimador puntual la varianza muestral de los retornos del activo. Sin embargo, los hechos estilizados de los activos financieros, tales como acciones, bonos o tasas de cambio, sugieren que la volatilidad no es constante. Por lo tanto, asumir homocedasticidad en el tiempo no es un supuesto muy realista.
Aunque la volatilidad de activos está bien definida, no es directamente observable en la práctica, pues se observa son los precios de un activo y sus derivados. El hecho de que la volatilidad no es directamente observable tiene varias implicaciones importantes en su estudio y modelización. Por lo tanto, para modelar las variaciones de las series financieras y acercarse un poco más a la realidad, se han desarrollado modelos, tanto de volatilidad histórica como condicional tales como los ARCH, GARCH, IGARCH, EGARCH, TGARCH, APARCH, los cuales permiten capturar las fluctuaciones presentes en la serie de retornos de cualquier activo con el fin de identificar la estructura condicional respecto al tiempo de cotización que se encuentra detrás de los retornos. La efectividad de los modelos de volatilidad condicional puede observarse en Álvarez, et al., 2007, Aragonés y Viñas, 1996, Awartani y Corradi, 2005, Franco, et al., 2007 y Gutiérrez y Gutiérrez, 2013.
Por otro lado, Cemex Colombia (Cemex, s.f.), filial de la cementera mexicana Cemex, es la segunda cementera más importante en Colombia del cual provee materiales de construcción y participa en la producción de cemento, mortero seco y concreto. Fundada en 1996, tiene su sede en Bogotá y administra cinco cementeras, 6 canteras de agregados, 69 plantas de hormigón premezclado y 8 centros de distribución terrestre. La acción de Cemex Latam Holdings comienza a transarse en el mercado colombiano de valores, bajo el nombre “CLH”, el día 15/11/2012, el cual es una buena alternativa de inversión teniendo en cuenta que hasta el momento sólo otra cementera, Argos, cotiza en la bolsa de valores de Colombia, además resalta el apetito para los inversionistas extranjeros teniendo en cuenta que, del total de la emisión, tan sólo el 15% de las acciones fueron adjudicadas a compradores colombianos.
Por tal motivo, el objetivo es obtener un modelo de volatilidad que explique las volatilidades diarias y logre capturar, con mínimo error, los retornos de precios de cierre diarios de las acciones CLH pertenecientes a la compañía de cemento CEMEX - Colombia, al tomar como periodo muestral entre 15/noviembre/2012 al 27/octubre/2017. Para ello, se aplica la volatilidad histórica con ventana móvil de 20 y modelos de volatilidad condicional como el GARCH, TGARCH, IGARCH, EGARCH y APARCH para seleccionar el modelo que mejor se ajusten a dicha serie.
2. Metodología
Dado el comportamiento de las series financieras, una de las principales preocupaciones de los inversionistas es tener un conocimiento aproximado del riesgo que presentan las inversiones que realizan. A partir de los precios diarios 𝑋𝑡 se puede calcular y modelar la volatilidad, al considerar los retornos representado por la ecuación 1:
| (1) |
donde, para ambos casos, 𝑋 𝑡−1 es el precio del activo en el tiempo 𝑡 − 1 y 𝑋𝑡 es el precio en el tiempo 𝑡.
Lo primero que se debe verificar es si la serie 𝑅𝑡 es estacionaria, esto es, si su media y su varianza son constantes en el tiempo. Para ello, se emplea el modelo (Ecuación 2):
| (2) |
y se usa la prueba de Dickey - Fuller el cual contrasta (Ecuación 3)
| (3) |
Un estadístico de prueba conveniente es distribución 𝑡 de DF de 𝜙1 bajo la hipótesis nula. Para la ecuación anterior (Ecuación 4 y 5),
| (4) |
| (5) |
donde 𝑅0 = 0 y 𝑇 es el tamaño de la muestra. El estadístico es (Ecuación 6):
| (6) |
La idea central detrás del estudio de la volatilidad es probar la heterocedasticidad condicional, esto es, autocorrelaciones significativas, de la serie 𝑅𝑡2. Para ello, la prueba Ljung-Box muestra en forma conjunta de que todos los coeficientes de autocorrelación son simultáneamente iguales a cero, esto es, son independientes dos a dos, al contrastar el siguiente planteamiento de hipótesis (Ecuación 7 y 8):
| \begin{equation} \begin{aligned} &\text { Ho: } \rho_{1}=\rho_{2}=\cdots=\rho_{k}=0 \\ &\text { Ha: } \rho_{i} \neq 0 \text { para algún } j=1,2, \cdots, k \end{aligned} \end{equation} | (7) |
donde
| (8) |
expresa la función de autocorrelación (ACF) hasta el rezago 𝑘 y estadístico igual a (Ecuación 9):
| (9) |
Para el cálculo de la volatilidad en la serie de retornos del periodo intramuestral, se procede a usar la volatilidad histórica o modelos de volatilidad condicional. Por un lado, como la volatilidad calculada para cada 𝑛 día, denominada ventana móvil, es más sensible si 𝑛 ↘ 0, se recomienda tomar como referencia la volatilidad histórica de los retornos para cada 20 días , o HV20, calculada como (Ecuación 10):
| (10) |
Por otro lado, para aplicar los modelos de volatilidad condicional, es importante considerar la esperanza y varianza condicional de 𝑅𝑡 dado 𝐹 𝑡−1 (Ecuación 11):
| (11) |
donde 𝐹𝑡−1 es el conjunto de retornos pasados hasta el tiempo 𝑡 − 1.
De [10], se asume que 𝜇𝑡 y 𝑅𝑡 siguen un modelo ARMA(p,q), donde (Ecuación 12)
| (12) |
con |𝜙𝑖| < 1 y |𝜃𝑗| < 1.
De la ecuación (12) podemos deducir, de la ecuación (11), que (Ecuación 13):
| (13) |
donde 𝜎𝑡 es la volatilidad para la serie 𝑅𝑡. La expresión 𝑎𝑡 hace referencia a los shocks o las innovaciones de un retorno en el tiempo 𝑡. El modelo de 𝜇𝑡 en la ecuación (12) se denomina la ecuación media para 𝑅𝑡 y el modelo 𝜎𝑡2 es la ecuación de volatilidad para 𝑅𝑡.
Luego de proponer un modelo en media condicional 𝜇𝑡 y un modelo en varianza condicional o estocástica 𝜎𝑡2, se procede a la validación de este, utilizando los residuales estandarizados
Las pruebas para comprobar los supuestos son las siguientes:
Los estadísticos de Ljung-Box de para verificar la no existencia de autocorrelaciones significativas y validar la ecuación en media. Así mismo, los estadísticos de Ljung-Box de para probar la validez de la ecuación de la volatilidad condicional o estocástica y la adecuada distribución de , según sea el caso, planteada en los términos de error 𝜖𝑡 de los modelos de volatilidad condicional o estocástica.
Tsay (2013), describe varios modelos de volatilidad condicional tales como:
a) Modelo GARCH
El modelo de heteroscedasticidad condicional autorregresivo generalizado, conocido como GARCH(m,s), es dado por la ecuación 14.
| (14) |
donde 𝜖𝑡 es una sucesión de variables idénticamente distribuido con media cero y varianza uno, 𝛼0 > 0, 𝛼𝑖 ≥ 0, y para garantizar la condición de estacionariedad en media. En este caso, si y si . La última restricción en implica que la varianza condicional de 𝑎𝑡 es finita, mientras que la varianza condicional evoluciona con el tiempo. De Jiménez (2014), podemos suponer que 𝜖𝑡 sigue o una distribución normal, 𝜖𝑡 ∼ 𝒩(0,1), una distribución t-student estandarizada, 𝜖𝑡 ∼ <(0,1) , o una distribución de errores generalizada, 𝜖𝑡 ∼ GED𝜅(0,1).
b) Modelo IGARCH
El modelo IGARCH, modelo generalizado autorregresivo integrado de heterocedasticidad condicionada, estima de una forma conveniente el efecto apalancamiento, el cual usa como estimación el modelo GARCH con (Ecuación 15):
| (15) |
c) Modelo EGARCH
El modelo EGARCH, o modelo exponencial generalizado autorregresivo y condicionalmente heterocedástico, acaba con las asimetrías en la estimación del efecto de los shocks, referenciado como (Ecuación 16):
| (16) |
donde el signo positivo de 𝑎𝑡−𝑖 contribuye a de la log volatilidad, mientras que el signo negativo de 𝑎𝑡−𝑖 contribuye a , donde y, el parámetro 𝛾𝑖 significa el efecto de apalancamiento de 𝑎𝑡−𝑖.
d) Modelo TGARCH
La idea del modelo TGARCH es dividir la distribución de los shocks en intervalos disjuntos para aproximar una función lineal por tramos para la desviación estándar condicional o para la volatilidad condicional. Si sólo hay dos intervalos, la división es normalmente en un umbral identificado con el número cero, donde la influencia de los shocks positivos se identifica con valores por encima de cero y negativos por debajo de este valor. En este caso, el modelo TGARCH(m,s) se puede escribir como (Ecuación 17):
| (17) |
donde 𝑁𝑡−𝑖 es un indicador para 𝑎𝑡−𝑖 definido por (Ecuación 18):
| (18) |
y 𝛼 𝑖, 𝛾 𝑖, 𝛽𝑗 son parámetros no negativos que satisfacen condiciones similares a los modelos GARCH.
e) Modelo APARCH
El modelo TGARCH pertenece a la clase de modelos de poder asimétrico autoregresivo condicional heteroscedastico, denominado APARCH(m,s), el cual se describe como (Ecuación 19):
| (19) |
donde 𝛿 > 0 y los coeficientes 𝛼0, 𝛼𝑖, 𝛾𝑖 y 𝛽𝑗 satisfacen ciertas condiciones de regularidad para que la volatilidad sea positiva.
3. Presentación de la información
La serie temporal a utilizar son los retornos diarios de las acciones colombianas CLH de multinacional CEMEX. Para el cálculo de esta serie de retornos, se utiliza los precios de cierre diarios de acciones, denominada 𝑋𝑡, en los que existe mercado en el periodo comprendido entre 03/abril/2014 al 23/octubre/2017, con un total de 1208 datos, obtenidos de la Bolsa de Valores de Colombia (s.f.).
Al aplicar la prueba de Dickey-Fuller, dada en la ecuación (3), que contrasta
Ho : La serie 𝑋𝑡 sigue un proceso no estacionario,Ha : La serie 𝑋𝑡 sigue un proceso estacionario,
Se concluye que, con un nivel de significancia del 5%, la serie de los precios no se comporta estadísticamente como un proceso estacionario, con una probabilidad de 41.17%. Por tanto, es de total interés analizar los retornos de la serie 𝑅𝑡 dada por la ecuación (1).
De igual forma, al usar la prueba de Dickey-Fuller, el cual contrasta,
Ho : La serie 𝑅𝑡 sigue un proceso no estacionario,Ha : La serie 𝑅𝑡 sigue un proceso estacionario,
Se concluye que, con un nivel de significancia del 5%, la serie se comporta estadísticamente como un proceso estacionario, con una probabilidad del 1%.
En la tabla 1 se observan que la serie 𝑋𝑡 y 𝑅𝑡 no siguen una distribución normal, contrastando esto por los histogramas mostrados en la figura 1 con relación a una distribución normal, el cual se evidencia que las series son asimétricas a la izquierda, además de platicurtica y lepticurtica, respectivamente.
Tabla 1. Descriptivas acciones CLH| Media | 13358.77 | 0.000087153 |
|---|---|---|
| Mediana | 12860 | 0 |
| Varianza | 5916878 | 0.0003110342 |
| Des. estándar | 2432.463 | 0.01763616 |
| IQR | 3270 | 0.01840395 |
| Asimétrica | 0.6812191 | 0-0.002137826 |
| Curtosis | -0.2625837 | 2.425206 |
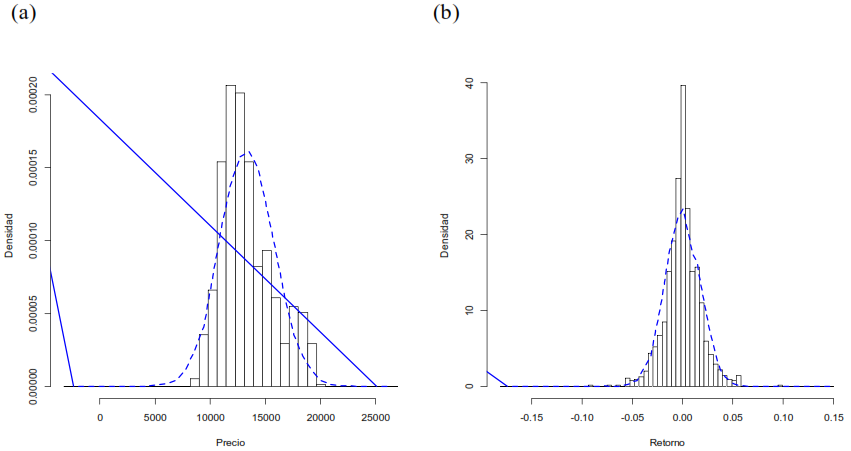
Figura 1. Histograma de acciones CLH a). Precios de cierre b). Retornos
Fuente: Elaboración propia a partir de los datos de CLH
4. Resultados y análisis
La serie de retornos 𝑅𝑡 en el periodo evaluado cuenta con 1542 datos. En la figura 2 se observa la serie de los precios de cierre y la serie de retornos el cual se evidencia fluctuaciones significativas.
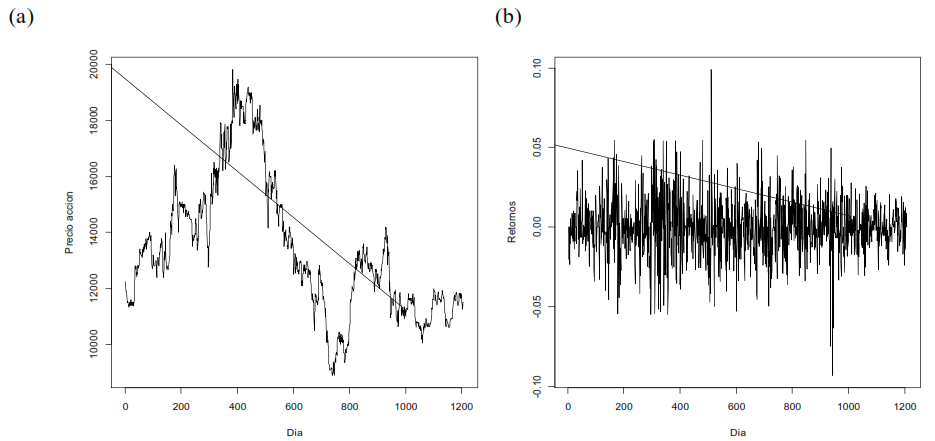
Figura 2. Serie de precios y retornos CLH a) Precio de cierre b) Retorno
Fuente: Elaboración propia a partir de los datos de CLH
En la figura 3 se observa que la función de autocorrelacion simple de la serie 𝑅𝑡 poseen pocos rezagos significativos que se encuentran por fuera de las bandas de confianza al 95%, sin embargo, se aplica la prueba de Ljung-Box, dada en la ecuación (7), para comprobar la significancia de las autocorrelaciones hasta el rezago 20.
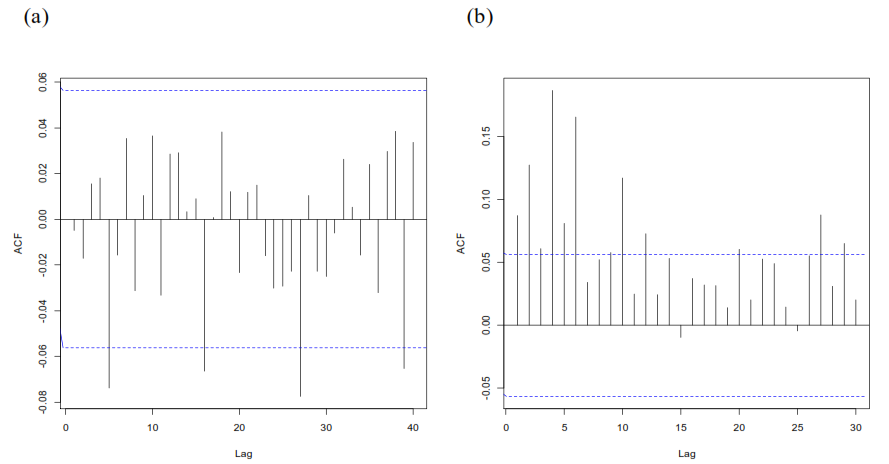
Figura 3. Función de autocorrelación (ACF) a) Precio de cierre b) Retornos
Fuente: Elaboración propia
La probabilidad asociada al estadístico de prueba es del 24.06% el cual permite concluir, con un nivel de significancia del 5%, que los retornos no presentan rezagos significativos, por tanto , no hay presencia de autocorrelación serial. Se observan autocorrelaciones significativas en los retornos al cuadrado, hasta el rezago 20 y con una probabilidad menor que 1%, indicando que no existe independencia serial en dicha serie.
Con el fin de identificar un modelo de volatilidad condicional apropiado, se inició a estimar los parámetros, por el método de máxima verosimilitud [7], de los modelos GARCH (m, s), IGARCH (m, s), EGARCH (m, s), TGARCH (m, s) y APARCH (m, s) dados en las ecuaciones (14), (15), (16), (17) y (19), respectivamente, con µ𝑡= 0, conforme al resultado de la prueba de Ljung-Box para la serie 𝑅𝑡, y para valores de 𝑚, 𝑠 = 1, 2, que son los primeros rezagos significativos observados en la ACP de la serie . Como las series de retornos financieros poseen unas regularidades empíricas llamadas hechos estilizados, la cual se encuentran colas pesadas de la distribución de los retornos donde esta suele ser más leptocurtica que la normal, se propone el uso de la distribución t -student estandarizada y la distribución GED a las variables 𝜖𝑡.En la tabla 2 se muestran los valores dados por los criterios de información bayesiana BIC para cada uno de los modelos mencionados, respectivamente, por medio del paquete rugarch del programa estadístico R versión 3.4.1 (Ghalanos, 2013).
Tabla 2. BIC modelos de volatilidad condicional para los retornos| |
||||
| GARCH | ||||
|---|---|---|---|---|
| IGARCH | ||||
| EGARCH | ||||
| TGARCH | ||||
| APARCH | ||||
Tomando los menores valores dados por el criterio de información bayesiano (BIC) para cada modelo, se seleccionan los modelos GARCH (1, 1), TGARCH (1, 1), EGARCH (1, 1), IGARCH (1, 1) y APARCH (1, 1) con 𝜖𝑡 ∼ 𝐺𝐸𝐷𝜅(0, 1). En la tabla 3 se muestran los parámetros estimados, incluyendo su nivel de significancia, para cada uno de los modelos, respectivamente, de los cuales se concluye:
Tabla 3. Estimación de parámetros modelos de volatilidad condicionalEn el modelo IGARCH (1,1) de la forma establecida como en la ecuación 20:
| (20) |
Los parámetros estimados son significativos, como lo observado en la tabla 3, para un nivel de significancia del 5%.
El modelo EGARCH (1,1) dado por la ecuación 21:
| (21) |
Posee parámetros significativos para un nivel de significancia del 5%.
El modelo TGARCH (1,1) de la forma (Ecuación 22),
| (22) |
posee el parámetro 𝛾1 no significativo, para un nivel de significancia del 5%, luego podría ser reducido a un modelo GARCH (1,1) dado por (Ecuación 23):
| (23) |
El modelo APARCH (1,1) formulado por (Ecuación 24):
| (24) |
Posee parámetros estimados son significativos para un nivel de significancia del 5%.
En base a la significancia de los parámetros y el menor BIC, el modelo que mejor se ajusta para explicar la volatilidad condicional de los retornos es un IGARCH (1,1) especificado en la ecuación 20.
Como lo observado en la figura 5, la función de autocorrelación parcial de los residuales estandarizados al cuadrado, dado en la ecuación (8), poseen pocos rezagos significativos, por lo tanto, el modelo de heterocedasticidad condicional está bien especificado; sin embargo, se aplicó la prueba de Ljung-Box para verificar este resultado.
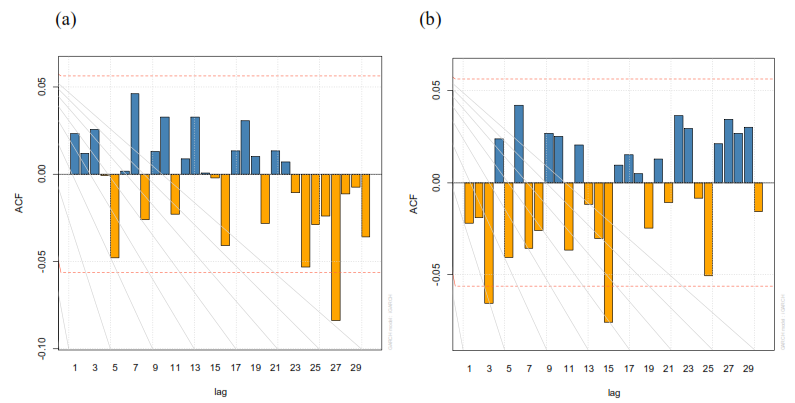
Fuente: Elaboración propia
La probabilidad resultante es del 13.25% el cual indica, a un nivel de significancia del 5%, que las autocorrelaciones conjuntas hasta el rezago 20 de los residuales estandarizados al cuadrado no son significativas. Esto indica que el modelo en varianza se encuentra adecuadamente especificado.
Así mismo, no se considera un modelo en media condicional 𝜇𝑡 ya que no existen correlaciones significativas con respecto a los residuales estandarizados, sin embargo, se procedió aplicar la prueba Ljung-Box para evaluar formalmente la significancia de dichas correlaciones hasta el rezago 20.
La probabilidad resultante es del 71.76% el cual indica que no existe suficiente evidencia para rechazar la hipótesis nula y por lo tanto, las autocorrelaciones conjuntas hasta el rezago 20 de los residuales estandarizados no son significativas indicando que el modelo en media condicional dado por 𝜇𝑡 = 0 se encuentra correctamente especificado.
La Figura 6(a) se observa que las estimaciones puntuales de las volatilidades 𝜎𝑡 dadas por la ecuación (20) logra abarcar las fluctuaciones generada por los retornos a un nivel de confianza del 95%, confirmando un buen ajuste del modelo.
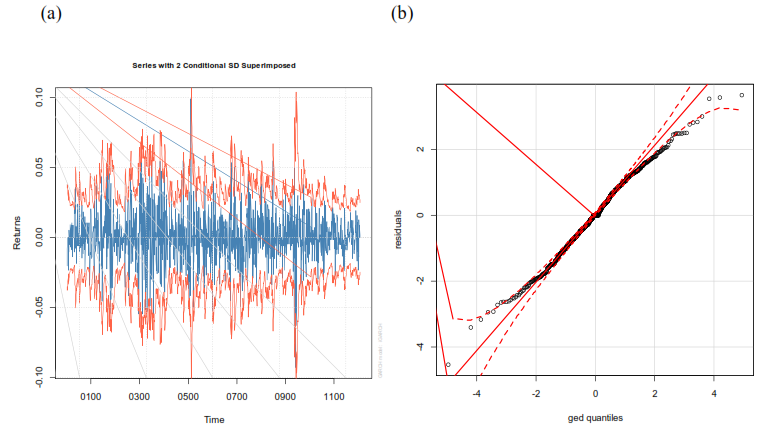
Fuente: Elaboración propia
Por otro lado, la verificación de la distribución de los errores (GED) con parámetro 𝜅 = 1.020353 se realizó de manera gráfica y se presentan en la figura 6b se observa que los residuales estandarizados se ajustan correctamente a dicha distribución, a un nivel de confianza del 95%.
Con relación a la volatilidad histórica con ventana móvil 20, o HV20, se observa en la figura 7 que el modelo IGARCH (1,1) cubre el 100% de las fluctuaciones de los retornos, en diferencia de un 97.21% de información cubierta dados por el modelo HV20, debido a que no logró capturar la mayoría de los cambios abruptos o caídas en los precios de cierre de las acciones CLH, lo cual confirma que el modelo IGARCH (1,1) logra explicar, con mínimo error, las volatilidades de la serie de retornos 𝑅𝑡.
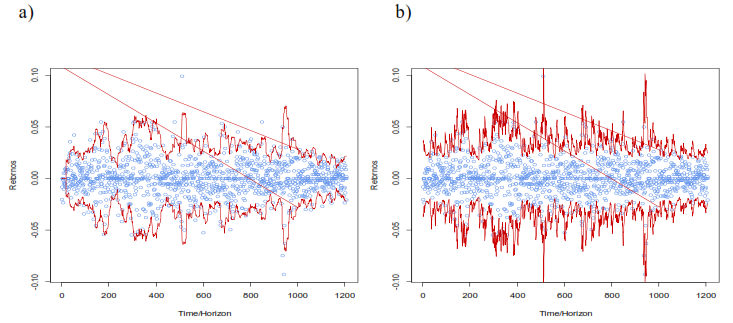
Fuente: Elaboración del autor
5. Conclusiones
El modelo IGARCH (1,1) es adecuado para ajustar la heterocedasticidad condicional de los retornos de los precios de la acción CLH, pues cumple con los supuestos en sus residuales estandarizados y captura adecuadamente los efectos de apalancamiento producidos por las fluctuaciones en el mercado lo cual influye en el alza o las bajas de precios de cierre, respectivamente. Este modelo hace que los shocks en la volatilidad del retorno de las acciones CLH sean persistente para un largo periodo en el futuro, además que la volatilidad no muestra reversión a la media, por lo que transcurren periodos largos antes que vuelva a tomar su valor promedio. Sin embargo, estas innovaciones no capturan adecuadamente los efectos de apalancamiento producidos por las fluctuaciones en el mercado, lo cual influye en el alza o las bajas de precios de cierre, respectivamente.
Por otro lado, el número de observaciones también puede ser un limitante en el ajuste del modelo, tanto condicional como estocástica, impidiendo una mejor captura de la volatilidad en los retornos de la acción diaria de Cementos Argos.
El modelo ajustado resultante es de gran ayuda para los inversionistas, pues da una idea del rendimiento medio de los retornos de la acción diaria de CLH facilitando la toma de decisiones a la hora de invertir.
6. Referencias Bibliográficas
Álvarez Franco P., Restrepo D., Ocaris Pérez F. (2007). Estudio de efectos asimétricos y día de la semana en el índice de volatilidad VIX. Revista Ingenierías Universidad de Medellín, vol. 6, núm. 11, pp. 125-147, Universidad de Medellín. Medellín, Colombia, 2007. https://doi.org/10.22395/rium.v16n31a4
Aragonés J.R., Viñas, C. (1996). Estimación de la volatilidad condicional en el Mercado de divisas con modelos de la familia GARCH. Investigaciones Europeas de Dirección y Economía de la Empresa Vol. 2, N°3, pp. 43 -59. https://doi.org/10.1016/j.iedee.2015.02.001
Awartani, B.M.A. and Corradi, V. (2005). Predicting the volatility of the S&P-500 stock index via GARCH models: the role of asymmetries. International Journal of Forecasting, 21, 167-183. https://doi.org/10.1016/j.ijforecast.2004.08.003
Bolsa de Valores de Colombia, http://www.bvc.com.co
Cementera CEMEX – Colombia, (s.f.). http://www.cemexcolombia.com/Index.aspx
Franco, P. B. A., Restrepo, D. A., and Perez, F. O. (2007). Estudio de efectos asimetricos y dia de la semana en el indice de volatilidad “vix”. Revista Ingenierias Universidad de Medellin, 6(11):125–147. https://doi.org/10.22395/rium.v13n25a5
Ghalanos A, (2013). Introduction to the rugarch package, R package version 1.3-1, August 16.
Gutiérrez R., Carvajal Gutiérrez L. (2013). Modelación y predicción de la volatilidad con innovaciones de colas pesadas distribuidas: evidencia empírica para los petróleos Maya y Mezcla Mexicana de Exportación. Paradigma económico, Núm. 1, pp. 67-105.
Jiménez Moscoso, J. A. (2014). Distribuciones de probabilidad alternativas para la gestión de riesgo en mercados financieros. PhD thesis, Universidad de Valencia.
Tsay, R.S. (2013). An Introduction to analysis of financial data with R. Editorial Wiley, New Jersey.
1 Docente, Departamento de matemática y estadística. MSc en Matemática, Universidade Federal de Minas Gerais, Belo Horizonte – Brasil. Email: christian.cortes@usco.edu.co[Link]
* (Autor de correspondencia)
2 Docente, Departamento de matemática y estadística. MSc (c) en Estadística, Universidad del Valle, Cali – Colombia. E-mail: alvaro.cangrejo@usco.edu.co[Link]