Modelado de cargas controlables en el despacho de sistemas con fuentes renovables y vehículos eléctricos
Controllable Loads Modeling in the Dispatch of Systems with Renewable Sources and Electric Vehicles
Wilder Guzmán1, Sebastián Osorio2 Sergio Rivera3
Resumen
El presente documento muestra el despacho económico realizado en un sistema de potencia con penetración de fuentes renovables y carros eléctricos, con énfasis en el modelado de cargas controlables. Para ello, se estudió el comportamiento de la irradiancia solar, la velocidad del viento y los patrones de conducción de carros eléctricos por medio de distribuciones de probabilidad Log-Normal, Weibull y Normal, respectivamente. Se definió el concepto de carga controlable, así como los requisitos del contrato con el operador de red para que un centro de consumo pueda declararse como controlable, mediante el uso de un modelo de minimización de costos de compensación por bloque de potencia no despachada, que permitiera modelar el comportamiento energético-económico de dichos nodos desde el punto de vista del operador de red. La optimización del despacho (flujo óptimo de potencia), se hizo por medio del algoritmo de optimización DEEPSO (Differential Evolutionary Particle Swarm Optimization) mediante la inclusión de 7 nodos controlables, escogidos en base a la posible flexibilidad de carga en el nodo respectivo. Se encontró que las cargas controlables pueden presentar dos grandes beneficios para el sistema dependiendo de los parámetros establecidos en el contrato permitiendo la suavización del perfil de demanda (desplazamiento de picos de máxima potencia y disminución de pérdidas) y disminución del costo total de generación.
Palabras clave: Optimización heurística; despacho económico; fuentes renovables de energía; cargas controlables
Abstract
This document shows the economic dispatch carried out in a power system with penetration of renewable sources, electric cars and with special emphasis on the modeling of controllable loads. For this, the behavior of solar irradiance, wind speed and electric carriage driving patterns were studied by means of Log-Normal, Weibull and Normal probability distributions, respectively. The concept of controllable load was defined as well as the requirements of the contract with the network operator so that a consumption center could be declared as controllable and a model of minimization of costs of compensation by unbundled power block was used to model the behavior energetic-economic of said nodes from the point of view of the network operator. The optimization of the dispatch (optimum flow of power) was made by means of the DEEPSO optimization algorithm by the inclusion of 7 controllable nodes, chosen based on an established selection criterion. It was found that the controllable loads can present two great benefits for the system depending on the parameters established in the contract: smoothing the demand profile (displacement of maximum power peaks and decrease of losses) and decrease of the total cost of generation.
Keywords: heuristic optimization; economic dispatch; renewable energy resources; controlable loads
1. Introducción
Las Fuentes Renovables de Energía (Renewable Energy Resources, RER) introducen en el despacho económico (Economical Dispatch, ED) de un sistema de potencia, variables no deterministas debido a la estocacidad de las fuentes primarias usadas por las RER. Anteriormente, con el uso de fuentes convencionales (termoeléctricas e hidroeléctricas) el error asociado al ED programado dependía exclusivamente de la demanda, pues determinaba la cantidad de potencia a inyectar en la red y consecuentemente el error solo dependía del pronóstico de la misma. Sin embargo, con la entrada masiva de las RER en los sistemas eléctricos, se establecen otras fuentes de error que afectan la programación del ED y que están representadas por la predicción de la velocidad del viento y la radiación solar (Shahirinia, Soofi , & Yu, 2016) (Dean, Ortmeyer, & Wu, 2016). Estas variables dependen de las condiciones climáticas específicas de cada lugar y su comportamiento puede ser modelado por Funciones de Densidad de Probabilidad (Probability Density Function, PDF), de modo que se pueden predecir los valores futuros necesarios para realizar un despacho económico óptimo con un error asociado, el cual se puede expresar a partir de funciones de costo por sobreestimar o subestimar (Rivera & Romero, 2018).
El DSM (Demand Side Management) usado para suavizar los perfiles de carga y lograr la minimización de pérdidas, ha cobrado gran relevancia. El DSM ofrece el potencial de sumar una gran cantidad de cargas flexibles para lograr así un despacho económico más óptimo. Los vehículos eléctricos (Electric Vehicles, EV), considerados como una forma de DSM (Galus, Koch, & Andersson, 2011) (International Energy Agency, 2015), se comportan como centros de consumo cuando se cargan, pero son capaces de inyectarle energía a la red en modo V2G (Vehicle-to-Grid). En numerosas investigaciones se ha estudiado el comportamiento de carga/descarga de estos dispositivos y puede ser modelado con una PDF de tipo Gaussiana (Dean, Ortmeyer, & Wu, 2016). Por su parte, una carga controlable pasiva, es aquel centro de consumo que se declara controlable o interrumpible a través de un contrato escrito con el operador de red (Distribution Utility, DU), estableciendo parámetrosen el contrato firmado por los dos agentes.
El despacho económico consiste en un proceso de asignación óptima de recursos, en donde se distribuye la energía eléctrica desde los centros de generación hasta los centros de consumo. La idea central es obtener una combinación óptima de generadores para suplir la demanda sujeta a restricciones propias del sistema de potencia.
Según la Agencia Internacional de Energía (2015), para el 2013 aproximadamente el 70% de la electricidad despachada en el mundo se produjo a partir de combustibles fósiles (42% carbón, 22% gas natural y 5% petróleo) y un 10% a partir de plantas nucleares (International Energy Agency, 2015). La cantidad de energía que una planta de estas puede entregar se calcula a partir de expresiones matemáticas fijas y conocidas. Por su parte, las hidroeléctricas que cuentan con embalse también poseen la función de potencia entregada conocida, mientras que las hidroeléctricas a filo de agua no. Estas últimas dependen del caudal del río, y de las condiciones climáticas de la localidad. No obstante, a pesar de que la potencia calculada no es enteramente conocida, sí se puede hacer una aproximación debido a que el ciclo del agua y la medición de los caudales de los ríos se ha estudiado hace más de 50 años y se posee una voluptuosa base de datos histórica que permite realizar pronósticos muy acertados. Sin embargo, las RER son centros de generación completamente impredecibles y, a diferencia de las plantas convencionales, no poseen ningún tipo de embalse, ni toneladas de carbón o galones de diésel que puedan respaldar su intermitencia. Asimismo, como no se tiene una gran serie histórica de medición de viento y radiación solar, el despacho de las RER involucra inexorablemente un tratamiento probabilístico.
Las funciones de densidad de probabilidad que caracterizan el comportamiento de la velocidad del viento, la radiación solar y la carga/descarga de los vehículos eléctricos han sido estudiadas en numerosas investigaciones relacionados con el despacho económico. Rivera y Arévalo (2018) adoptan una distribución de probabilidad Weibull para la velocidad del viento, una distribución de probabilidad Log-normal para la radiación solar y una distribución Normal para los EV, que después integran en un despacho económico estático para calcular las funciones por sobreestimación y subestimación. En Shahirinia (2016), se realiza un despacho económico estocástico que lidia con las incertidumbres de los generadores eólicos. Dicho acercamiento hace uso de datos de velocidad de viento simulados que se integran en el despacho económico para estimar las distribuciones de probabilidad de la generación óptima de plantas fósiles, pérdidas por transmisión y el costo total de la generación del sistema. Surender Reddy y Bijwe (2015) plantean la evaluación del mejor ajuste de los factores de participación, en el despacho considerando la variabilidad minuto a minuto de plantas solares, eólicas y la demanda, para un periodo de programación dado. Por su parte, Xu Wang (2016) da más relevancia al recurso eólico y proponen un nuevo modelo para el despacho activo optimizado que combina la optimización robusta con la optimización dinámica para revelar los efectos de la demanda que responde al precio, mientras consideran todas las restricciones y aleatoriedad de los aerogeneradores. En Ruifeng (2016) se propone un modelo para tratar con el problema de la integración de grandes cantidades de nodos de generación eólica y de conexión EV por medio de la optimización robusta. En Minghong (2012) se presenta un despacho económico incluyendo los PHEV* (Plug-in Hybrid Eletric Vehicles), así como una revisión histórica de los sistemas eléctricos integrados con carros eléctricos. Rivera y Romero (2018), plantean un ED en donde incorporan generación solar, eólica (Wind Energy Generation, WEG) y EV. Ellos hacen uso de un algoritmo de optimización heurística y concluyen con el costo esperado de generación, así como el valor esperado de penalización.
Las cargas controlables (Controllable Loads, CL) o interrumpibles (Interruptible Loads, IL), brindan la flexibilidad necesaria para ajustar la curva de carga del sistema y de aprovechar la participación de grandes centros de consumo (Yao, Liu, Lu, & Yuan, 2015). Las IL son una de las principales formas del cambio de pico de demanda máxima y juegan un importante papel en las horas de gran demanda, pues reducen el estrés eléctrico del sistema. Yao, Liu, Lu y Yuan (2015), presentan un modelo de optimización para que los DU puedan determinar la participación de cargas industriales en la demanda máxima y se discute la característica tiempo-espacio de las CL, incluyendo el refinamiento de la capacidad mínima de carga y la duración de la interrupción. Pan, Li y Wang (2012), proponen que el despacho de las IL puede ser dividido en 3 niveles de tiempo: nivel de día adelante (day-ahead level), nivel horario (hour level) y nivel de cuarto de hora (15 min level), por tanto, se realiza la optimización del despacho de las CL en diferentes escalas de tiempo.
La inclusión de las IL en el despacho económico ya ha sido abordada por numerosos estudios especialmente sobre microrredes y smart grids, pero su principio básico puede ser aplicado a un sistema de potencia de mayor complejidad. Así, Ziadi, et al. (2014) propone una técnica de decisión para la programación óptima de sistemas distribuidos, sistemas de almacenamiento con baterías, cargas controlables y cambio de taps de transformadores de potencia, en donde su principal objetivo es alcanzar una reducción significativa de pérdidas del sistema de distribución. Sharma, et al. (2015) presenta un nuevo marco de modelado para el análisis del impacto y la programación de cargas elásticas (cargas price-responsive) así como de las CL en un sistema desbalanceado de distribución. Las cargas elásticas se asumen como lineales o exponenciales dependiendo de la interacción de su potencia demandada con el precio de la electricidad. La minimización del costo de la energía extraído por la compañía de distribución local, las pérdidas en los alimentadores y el costo de los clientes en relación con el componente de la carga, son considerados como objetivos desde la perspectiva de la compañía de distribución. Por su parte, Saber & Kumar (2013) proponen una optimización del despacho con cargas controlables usando la optimización por enjambre de partículas (Particle Swarm Optimization, PSO). Allí consideran una micro red inteligente y se establece el costo de operación y de capital como función objetivo, sujeta a un gran número de restricciones incluyendo emisiones contaminantes netas iguales a cero. Para ello, se utiliza la velocidad del viento histórica, la radiación solar y los perfiles de carga durante un largo periodo de tiempo como entradas del modelo y se lleva a cabo un sistema inteligente de gestión de la energía para el despacho de los recursos.
Un flujo óptimo de potencia (Optimal Power Flower, OPF) involucra un número considerable de restricciones no lineales, variables continuas y discretas, ecuaciones convexas y polinomiales y, en general, complejidades propias de un sistema de potencia real. Los procedimientos anteriormente usados para resolverlo incluían expresiones analíticas y restricciones duras que tomarían años en dar una solución, pero las técnicas heurísticas se basan en comportamientos biológicos que hacen uso de habilidades sociales para llegar a una buena solución, mas no necesariamente la óptima.
Todos los trabajos anteriormente nombrados hacen uso de algún tipo de heurística específica o metaheurística, por ejemplo, la optimización por enjambre de partículas o por evolución diferencial. Estas técnicas de solución no analíticas ofrecen la posibilidad de incluir restricciones suaves, las cuales permiten incorporar restricciones no lineales. El presente trabajo hace uso del algoritmo de optimización DEEPSO, que hace parte a su vez de un selecto grupo (CBGA-Consensus-Based Grouping Algorithm), DEEPSO, ICDE (Improved.Constrained Differencial Evolution Algorithm), MINLP (Mixed Integer Non-Linear Programms), MVMO (Mean-Variance Optimization Algorithm), que sirven para realizar el ED en sistemas de potencia con o sin penetración de energías renovables. Dichos algoritmos fueron seleccionados por la IEEE (Institute of Electrical and Electronics Engineers) en la competencia mundial que pretendía encontrar los mejores algoritmos de optimización heurística desarrollados por los diferentes grupos de investigación del mundo. El concurso fue lanzado y dirigido por el grupo de investigación en técnicas de optimización heurística de la IEEE – PES (Power and Energy Society) en febrero del 2014.
2. Metodología
Se evidencia que a pesar de que la inclusión de cargas controlables en el ED se ha realizado, no se ha hecho en conjunto con plantas alternativas y carros eléctricos. La estocacidad de las RER y el análisis de vehículos conectados a la red ya se ha tratado con éxito, pero sin incluir cargas controlables en ningún nodo. Este trabajo incorpora un modelo para cargas controlables, de manera que el operador de red puede conocer la cantidad de potencia óptima – visto desde el punto de vista del sistema global- que debe ser despachada a una carga que se haya declarado interrumpible.
El presente trabajo es un agregado del tratamiento desarrollado por Arévalo y Santos (2017), en el cual exponen la inclusión de nodos con generación renovable en el ED, que sirven como información de entrada para el presente ED, sin modificar ninguna función de costos, ni de penalización usadas por dichos autores y sumándole el modelo de cargas controlables descritos en la literatura y adoptado para ser usado por algoritmo de solución.
Así, el OPF que se propone consiste en la minimización del valor esperado del costo total de generación, mostrado a continuación:
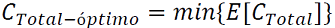 (1)
(1)
donde
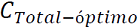 es el costo total de generación optimizado.
es el costo total de generación optimizado.
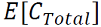 es el valor esperado de la función de costos de generación total del sistema.
es el valor esperado de la función de costos de generación total del sistema.
La función de costos de generación total del sistema es la suma de los costos de los generadores convencionales más los costos por sobre y subestimar en los nodos de generación renovable y EV más el costo por compensación resultado del modelado de las cargas controlables, que se muestra en la expresión (2):
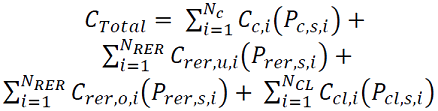 (2)
(2)
donde
NC es el número de generadores convencionales.
NRER es el número de generadores renovables.
NCL es el número de nodos declarados como cargas interrumpibles.
CCi es la función de costos del generador convencional i.
C𝑟𝑒𝑟,𝑢,𝑖 es la función de costos por subestimar del generador renovable i.
C𝑟𝑒𝑟,o,𝑖 es la función de costos por sobreestimar del generador renovable i.
C𝑐𝑙,𝑖 es la función del costo por compensación del nodo controlable i.
P𝑐,𝑠,𝑖 es la potencia programada del generador convencional i.
P𝑟𝑒𝑟,𝑠,𝑖 es la potencia programada del generador renovable i.
P𝑐𝑙,𝑠,𝑖 es la potencia programada para entregar al nodo controlable i.
La función de costos de un generador convencional está dada por una expresión polinómica de orden 2, como sigue:
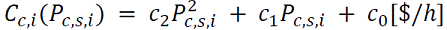 (3)
(3)
En donde el valor de los coeficientes 𝑐𝑖 depende de la energía primaria usada por la planta (carbón, gas, combustibles líquidos, etc.), así como el tipo de ciclo termodinámico usado.
La función de costos por subestimar de los generadores renovables se divide en funciones de costos por subestimar de generadores fotovoltaicos, generadores eólicos y carros eléctricos. Las expresiones por sobreestimar de generadores renovables siguen la misma lógica y se pueden consultar en el artículo de Arévalo y Santos (2017). Los costos de generación de las plantas renovales se asumieron como cero, debido a su bajo costo operativo. Por último, el costo por compensación de los nodos controlables depende de la cantidad de potencia que se le deja de suministrar, como se observa más adelante.
2.1. Descripción del sistema de potencia bajo prueba
Se escogió el sistema de 118 nodos de la IEE como caso de estudio, el cual posee una potencia base de 100 MW, potencia instalada de 8205 MW y una demanda total de 4242 MW. En la Tabla 1. Características del sistema de 118 nodos. se muestran los elementos del sistema.
Tabla 1. Características del sistema de 118 nodos.
| Nodos | Cantidad |
| Generadores convencionales | 43 |
| Generadores fotovoltaicos | 5 |
| Generadores eólicos | 2 |
| Nodos con conexión de vehículos | 4 |
| Cargas controlables | 7 |
| Cargas no controlables | 92 |
| Líneas | 186 |
| Taps de transformadores | 9 |
| Compensadores en paralelo | 4 |
2.2. Algoritmo de optimización DEEPSO
El algoritmo de optimización DEEPSO es un híbrido que combina técnicas heurísticas evolutivas y de enjambre de partículas para realizar el despacho óptimo de potencia activa y reactiva minimizando la función de costo total de generación. El algoritmo involucra 137 variables de decisión continuas y discretas definidas como sigue:
- Continuas: representan las potencias inyectadas y magnitud de tensión en cada nodo. 42 son la potencias activas despachadas por los generadores convencionales (excluyendo el nodo Slack), 5 son la potencias activas despachadas por los generadores fotovoltaicos, 2 son la potencias despachadas por los generadores eólicos, 4 son la potencias activas en los nodos con conexión de vehículos, 7 son las potencias despachadas a cada nodo controlable y 54 variables están relacionadas con la magnitud de tensión en los nodos de generación, para un total de 114 variables de decisión continuas.
-
Discretas: 9 representan la relación del tap de transformación con mínimo de
=0,9 y máximo de
=1,1 y 14 variables discretas binarias asociadas a los dispositivos de compensación, para un total de 23 variables de decisión discretas.
El DEEPSO inicializa su búsqueda por medio de la generación de una población inicial aleatoria, sobre la cual se itera y se dirige la búsqueda por medio de técnicas inteligentes hacia óptimos locales. Para la solución en cada flujo de potencia se implementa la herramienta Matpower de Matlab, empleando el modelo típico de análisis en estado estático, luego se evalúa la función objetivo por medio de la determinación del valor de la función de costos de generación (𝐶𝑇𝑜𝑡𝑎𝑙) y paso seguido se evalúa la función de aptitudes (𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠). Esta última consiste en la suma de la función objetivo y una función de penalización, la cual es mostrada en la ecuación siguiente:
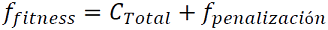 (4)
(4)
donde
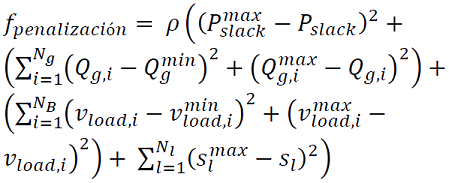 (5)
(5)
La función de aptitudes toma en cuenta las limitaciones de generación de potencia activa en el nodo Slack (𝑃𝑠𝑙𝑎𝑐𝑘), la limitación de generación de potencia reactiva en los nodos de generación (𝑄𝑔,𝑖), la limitación de magnitud de la tensión en los nodos de carga (𝑣𝑙𝑜𝑎𝑑,𝑖) y la restricción de flujo de potencia en cada línea de transmisión (𝑠𝑙). 𝜌 es un factor de penalización fijado en 1𝑥107. 𝑁𝐵 es el número de nodos de carga del sistema y 𝑁𝑙 es el número de ramas del sistema. El diagrama de flujo se programa en 100.000 iteraciones para finalmente obtener la solución correspondiente al mejor valor de la función de aptitudes (Rivera Rodriguez, Arevalo, & Santos, 2018).
3. Modelado de las fuentes solares, eólicas y carros eléctricos (PVG, WEG, EV)
Debido a la intermitencia de las fuentes renovables, su modelado se relaciona inexorablemente con variables estocásticas. Estos modelos deben tener en cuenta la incertidumbre de la disponibilidad del recurso. Arévalo y Santos (2017), plantean un modelo de costos para la inclusión de fuentes renovables (PVG, WEG y EV) de energía en el despacho económico de un sistema de potencia, en función de los costos de compensación. Con el objetivo de considerar la incertidumbre característica del recurso renovable, es necesario involucrar dos variables que dependen de la disponibilidad del recurso en el modelo de cada fuente:
- Costos de compensación por subestimación: Es el costo de compensación que se debe pagar al programarse en el despacho económico una demanda de potencia inferior a la que se encuentra disponible del recurso.
- Costos de compensación por sobrestimación: Es el costo de compensación que se debe pagar al programarse en el despacho económico una demanda de potencia superior a la que se encuentra disponible del recurso.
Finalmente, la metodología planteada por Arévalo y Santos (2017), tiene como objetivo la minimización de costos de compensación por subestimar y sobrestimar, al incluir fuentes de energía renovables en un sistema de potencia.
3.1. Modelo de minimización de costos en fuentes de energía solar (PVG)
El modelo probabilístico que Rivera y Arévalo (2018), utilizaron para el desarrollo matemático del modelo de costos, se basa en una función de probabilidad log-normal, la cual se encuentra en función de la irradiancia solar:
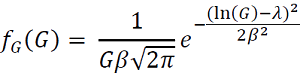 (6)
(6)
donde 𝑓𝐺(𝐺) es la función de probabilidad log-normal, 𝐺 representa la irradiancia solar, 𝜆 es la media de la distribución log-normal, y 𝛽 corresponde a la desviación estándar de la distribución log-normal. Finalmente, las ecuaciones de costos (tanto de los PVG como de los WEG y EV) se obtienen a partir de un amplio tratamiento matemático, que se puede consultar en detalle en Arévalo y Santos (2017)..
El modelo de costo del recurso solar, al provenir de una fuente intermitente, depende en su totalidad de la ubicación geográfica de los paneles fotovoltaicos. Arévalo y Santos (2017), se basaron en datos históricos de irradiancia solar en la región de la Guajira en Colombia para el planteamiento del modelo, por lo que los resultados expuestos tanto por ellos, como porel presente artículo son de alcance limitado, pero las conclusiones son válidas para cualquier sistema de potencia.
3.2. Modelo de minimización de costos en fuentes de energía eólica
La potencia generada por una turbina eólica en función de la velocidad del viento, son las variables punto de partida del modelo propuesto por Rivera (2018):
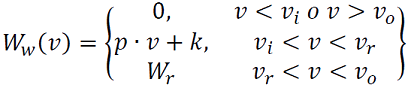 (7)
(7)
donde 𝑊𝑤(𝑣) corresponde a la potencia generada por la turbina eólica, 𝑣 corresponde a la velocidad del viento, 𝑣𝑖 corresponde a la velocidad del viento de corte inferior de la turbina, 𝑣𝑟 corresponde a la velocidad nominal de la turbina, 𝑣𝑜 corresponde a la velocidad del viento de corte superior de la turbina, y 𝑊𝑟 corresponde a la potencia nominal de la turbina. De igual manera que en el caso solar, se basaron en datos históricos de la velocidad del viento de la región caribe de Colombia, y las limitantes en cuanto a la aplicabilidad se deben a la ubicación geográfica de las turbinas eólicas.
3.3. Modelo de minimización de costos en nodos con conexión de vehículos eléctricos
El tercer modelo, se basa en la expansión del mercado de vehículos eléctricos y la inclusión de estos como cargas considerables dentro de un sistema de potencia. Debido al comportamiento estocástico de los patrones de conducción de los vehículos eléctricos, el modelo de obtuvo a partir de los de dos variables fundamentales en el cálculo de la necesidad recarga de las baterías:
-
Energía disponible en función de la distancia de recorrido del vehículo eléctrico: en donde se plantea la distancia recorrida como una distribución normal.
Donde 𝑓𝐷(𝐷) corresponde función de densidad de probabilidad de la distancia recorrida por el vehículo, 𝐷 corresponde a la distancia recorrida por el vehículo, 𝜇 corresponde a la media de distribución, y 𝜙 corresponde a la desviación estándar de la distribución.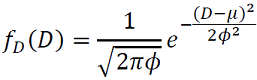 (8)
(8) -
Comportamiento de carga y descarga de la batería de los vehículos eléctricos: en donde se plantea la carga/descarga de la batería como una distribución normal.
Donde 𝑓𝑝𝑒(𝑃𝑒)corresponde con la función de probabilidad de la disponibilidad de las baterías de los vehículos eléctricos.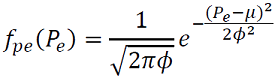 (9)
(9)
4. Modelado de las cargas controlables y su inclusión en un sistema de potencia
Las cargas controlables (CL) o también conocidas como cargas interrumpibles (IL), son centros de carga que permiten, mediante un contrato con el operador de red, la interrupción total o parcial de su demanda. Están diseñadas para suavizar el perfil de carga que se presenta durante los periodos pico de un sistema de potencia y con ello disminuir el porcentaje de pérdidas totales (Yao, Liu, Lu, & Yuan, 2015). La optimización del sistema partiendo de un despacho controlable de la demanda, no solamente aumenta los índices de confiabilidad del sistema, sino que también se refleja en la minimización de costos de generación.
Por lo general las cargas controlables son implementadas en los nodos que cuentan con cargas industriales de gran demanda las cuales se encuentran en capacidad de establecer acuerdos con el operador de red para programar cortes de potencia durante periodos pico.
4.1. Funcionamiento de las cargas controlables
Como se mencionó anteriormente, las cargas interrumpibles son implementadas por usuarios que demandan grandes cantidades de energía, estos usuarios deben encontrarse en capacidad de suplir su propia demanda durante los periodos de corte. El modelo de funcionamiento de la implementación de estas cargas se basa en la firma de un contrato por parte del usuario y del operador de red (DU), en donde básicamente se establece la capacidad de la carga interrumpible, los precios de compensación al usuario dependiendo de la cantidad de potencia interrumpida y los tiempos de notificación y duración de las interrupciones. Por lo tanto, la estructura del contrato de una carga controlable debe contar con los siguientes ítems (Yao, Liu, Lu, & Yuan, 2015):
- Duración del contrato.
- Tiempos de notificación antes de la interrupción.
- Tiempo de duración de la interrupción.
- La capacidad de la carga interrumpible.
- Costos de compensación.
- Restricciones operativas.
La inclusión de cargas controlables en un sistema de potencia depende tanto del operador de red como de los usuarios. El operador de red está en la capacidad de seleccionar los nodos en los cuales es óptimo incluir cargas controlables; por medio de estudios de flujos de carga es posible determinar que líneas se encuentran sobrecargadas. Por otro lado, el usuario que desee convertirse en carga controlable debe realizar un estudio del potencial de carga y determinar que es capaz de mantener por sí mismo un porcentaje de su demanda durante un periodo determinado de tiempo. Sin embargo, el usuario depende del visto bueno del operador de red para ser considerado carga controlable, ya que la ubicación de la carga en el sistema puede afectar de manera positiva o negativa la minimización de costos y de porcentaje de pérdidas del sistema.
4.1.1. Duración del contrato
La duración del contrato debe ser de común acuerdo entre el operador de red y el usuario, y su terminación está sujeta al momento en que por cambios en el sistema la interrupción de carga al usuario no sea beneficiosa para aliviar la sobrecarga del sistema.
4.1.2. Tiempos de notificación
Los tiempos de notificación deben ser acordados entre ambas partes, y deben tener en cuenta el tiempo que tarda el usuario en prender las máquinas de respaldo para soportar la interrupción. No obstante, el modelo que se plantea en este documento es del tipo day-ahead, es decir el análisis de interrupción de carga y la notificación se hace con un día de anticipación.
4.1.3. Tiempo de duración de las interrupciones
Los tiempos de duración de las interrupciones deben ser acordados entre ambas partes, y dependen de la capacidad del usuario para mantener la demanda interrumpida por sí mismo, y del tiempo mínimo durante el cual interrumpir al usuario sea beneficioso para el sistema.
4.1.4. Costos de compensación
El modelo de costos de compensación que se plantea en este documento, se basa en el “método de ajuste por bloque de capacidad” (“The method of capacity block refinement”) (Yao, Liu, Lu, & Yuan, 2015), el cual establece precios de compensación de acuerdo a bloques de capacidad de potencia interrumpidos, como se muestra en la Tabla 2. Precio de compensación por bloque de capacidad interrumpida., en donde 𝑃𝐼𝐿 es la demanda de la carga interrumpible.
Tabla 2. Precio de compensación por bloque de capacidad interrumpida.
| Usuario | Capacidad interrupción |
Precio de compensación |
| Bloque I | (70% – 90%)∗𝑃𝐼𝐿 | C1 |
| Bloque II | (50% – 70%)∗𝑃𝐼𝐿 | C2 |
| Bloque III | (0% – 50%)∗𝑃𝐼𝐿 | C3 |
4.2. Modelo de la carga controlable
El modelo de carga controlable utilizado en este documento se basa en el planteamiento de Yao, Liu, Lu, & Yuan (2015) de carga interrumpible como un modelo de minimización de costo de compensación debidos a la interrupción de carga. No obstante, se modifica el modelo original desde su concepción porque éste está enfocado a la minimización de costos de compensación por interrupción de potencia en un periodo de tiempo de 24 horas, sin afectar la energía promedio consumida por la carga en el periodo de análisis. Esto se debe a que la potencia se interrumpe en ciertos momentos, pero al final la energía que consume la carga es la misma que si no fuera carga interrumpible. Por otro lado, el presente planteamiento usa un tiempo de análisis menor (1 hora) y elimina la restricción de energía consumida. Esto debido a que es conveniente realizar flujos óptimos de carga menos espaciados en el tiempo para disminuir el error predictivo. El modelo de minimización de costos de compensación se plantea a continuación:
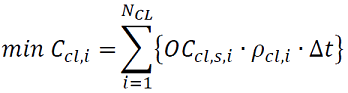 (10)
(10)
donde C𝑐𝑙,𝑖 corresponde con el costo de compensación de la carga controlable del nodo 𝑖; 𝑂𝐶𝑐𝑙,𝑠,𝑖=(1−𝑃𝑐𝑙,𝑠,𝑖) corresponde con la cantidad de carga programada que puede interrumpir el usuario 𝑖 durante el periodo de tiempo 𝑡, en 𝑀𝑊; 𝜌𝑐𝑙(𝑖) corresponde al costo de compensación por la interrupción de carga al usuario 𝑖 en $𝑀𝑊ℎ⁄; Δ𝑡 corresponde con la duración en horas del periodo durante el cual se realiza la interrupción de carga, en este caso Δ𝑡= 1 hora.
4.3. Restricciones de la inclusión de una carga controlable en el sistema.
Dadas las condiciones operativas de los generadores y las funciones de costos de los mismos, existe una mínima cantidad de energía que debe ser despachada diariamente para que el sistema sea tanto técnica como económicamente viable. Este punto mínimo de operación debe ser establecido por el ente comercializador de energía, y se denota como 𝑐𝑑í𝑎. La siguiente función expresa que el total de carga interrumpida debe ser mayor o igual a la mínima condición de operación del sistema (Yao, Liu, Lu, & Yuan, 2015):
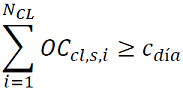 (11)
(11)
4.4. Restricciones de cantidad de carga interrumpida al usuario i.
Anteriormente se hizo mención de la necesidad de un estudio de potencial de carga interrumpible que tiene cada usuario, dicho estudio determina la cantidad de carga interrumpible diaria mínima que puede ser cortada Δ𝑃𝑜 al usuario durante determinados periodos del día. De acuerdo con (Yao, Liu, Lu, & Yuan, 2015) es posible determinar el potencial teniendo en cuenta las siguientes variables:
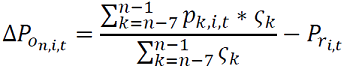 (12)
(12)
donde Δ𝑃𝑜𝑛,𝑖,𝑡 corresponde al potencial de carga interrumpible del usuario 𝑖 en el periodo 𝑡 del día 𝑛; 𝑝𝑘,𝑖,𝑡 corresponde al valor medido de la carga del usuario 𝑖 en el periodo 𝑡 del día 𝑘; 𝑃𝑟𝑖,𝑡 expresa la soportabilidad de carga del usuario 𝑖 en el periodo 𝑡; y 𝜍𝑘 es un coeficiente de peso.
Entonces, las restricciones de mínima cantidad de carga interrumpida al usuario 𝑖 durante el periodo 𝑡, están dadas por la siguiente expresión:
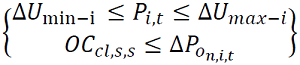 (13)
(13)
donde Δ𝑈min−i y Δ𝑈𝑚𝑎𝑥−𝑖corresponden a la mínima y a la máxima capacidad de carga interrumpible que posee el usuario i respectivamente.
5. Simulaciones y análisis de resultados
Se partió del caso base propuesto por Rivera y Arévalo (2018), en donde el sistema de potencia de 118 nodos de la IEEE presentado en la sección 2.1, se incluyeron 11 nodos asociados a fuentes renovables:
- Nodos asociados a fuentes de generación fotovoltaica: nodos 4, 99 y 110 (40 MW a 60 MW) y nodos 42 y 49 (140 MW a 200 MW).
- Nodos asociados a fuentes de generación eólica: nodos 24 y 26 (250 MW a 300 MW).
- Nodos asociados a conexión de vehículos eléctricos: nodos 59, 80, 90 y 116 (6.54 MW a 13.6 MW).
El objetivo del modelo es minimizar los costos totales de generación, pero como uno de los propósitos de las cargas controlables en un sistema de potencia es el de suavizar la curva de carga en las horas de mayor estrés del sistema, se adoptó un indicador indirecto para establecer el estado de sobrecarga de la red: el porcentaje de pérdidas activas totales (𝑰 2𝒁).
A continuación, se muestran los resultados de las simulaciones y el análisis del método propuesto para la determinación de los nodos con potencial para ser cargas controlables, en función de la minimización de pérdidas y costos de generación.
5.1. Determinación de la ubicación de los nodos interrumpibles
El primer paso para el análisis para determinar los nodos con potencial de carga controlable, se basó en la simulación del flujo de carga del sistema base por medio de la herramienta Matpower, con el objetivo de determinar las líneas de transmisión que presentan las mayores pérdidas activas y los nodos de demanda asociados a estas. En la Tabla 3. Líneas con mayor aporte a las pérdidas activas globales del sistema. se muestran las líneas que aportan las mayores pérdidas activas (𝑰 2𝒁) al global del sistema, considerando que el sistema tiene 186 líneas de transmisión.
Tabla 3. Líneas con mayor aporte a las pérdidas activas globales del sistema.
| Línea | 𝑰𝟐𝒁 [MW] |
Aporte |
| 25-27 | 6,400 | 5% |
| 69-75 | 4,851 | 4% |
| 8-9 | 4,620 | 3% |
| 23-25 | 4,204 | 3% |
| 89-92 | 3,978 | 3% |
| 69-70 | 3,431 | 3% |
| 42-49 | 3,170 | 2% |
| Global [MW] |
132.931 | |
Partiendo de la información de la Tabla 3. Líneas con mayor aporte a las pérdidas activas globales del sistema. se seleccionaron los 7 nodos de demanda asociados a las líneas, como los nodos con mayor potencial de carga controlable del sistema base (ver Tabla 4. Nodos con mayor potencial de carga controlable.).
Tabla 4. Nodos con mayor potencial de carga controlable.
| Nodo | Demanda [MW] |
| 27 | 71 |
| 75 | 47 |
| 8 | 28 |
| 23 | 7 |
| 92 | 65 |
| 70 | 66 |
| 42 | 96 |
5.2. Determinación del precio de compensación y costos de generación del caso base
El algoritmo DEEPSO del caso base propuesto por Arévalo y Santos, trae asociado coeficientes de penalización debidos a la subestimación y sobrestimación en el despacho con fuentes renovables de energía. El modelo de cargas controlables se plantea de manera tal que el operador de red debe pagar compensaciones monetarias a los usuarios controlables durante el periodo de interrupción de carga. El precio de compensación debe establecerse en proporción al costo asociado al usuario por suplir su propia demanda durante el periodo de interrupción.
Inicialmente, el precio de compensación se estableció de manera aleatoria dentro del algoritmo de simulación lo que conllevo a un 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 elevado. El anterior resultado llevo al análisis del costo asociado a cada unidad de generación propuesta en el caso base para establecer un precio de compensación proporcional. El sistema base de la IEEE de 118 nodos parte de la suposición de que los costos de encendido y apagado de las unidades de generación son iguales a cero, y poseen un precio promedio de generación 30 unidades monetarias por hora de generación.
El precio de compensación es variable y está dado en función del tamaño del bloque de demanda interrumpida, este precio se asocia a la cantidad de potencia no suministrada, y aumenta de manera directamente proporcional con un factor de ajuste debido a la suposición de que el precio de generación de una planta de respaldo (grupos alógenos) es mayor.
En la Tabla 5. Precio de compensación por bloque de carga interrumpida. se muestran los precios de compensación establecidos por bloque de carga interrumpida.
Al ejecutar el DEEPSO en el caso base, se obtienen los resultados presentados en la tabla 6.
Tabla 5. Precio de compensación por bloque de carga interrumpida.
| Capacidad interrupción |
Precio de compensación [$/h] |
|
| Bloque I | (70% – 90%)∗𝑃𝐼𝐿 | 3,30 |
| Bloque II | (50% – 70%)∗𝑃𝐼𝐿 | 10,80 |
| Bloque III | (0% – 50%)∗𝑃𝐼𝐿 | 19,50 |
Tabla 6. Resultados de simulación del caso base
| Ítem | Valor simulado |
| 𝐶𝑇𝑜𝑡𝑎𝑙 [$] | 150.169,97 |
| 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 [$] | 153.636,47 |
| 𝐼2𝑍 [MW] | 132.931 |
5.3. Optimización de costos por medio de la inclusión de un nodo con demanda controlable.
Se estableció un caso comparativo para determinar el efecto de una sola demanda interrumpible en un sistema de potencia de gran tamaño. Para ello, se plantearon dos escenarios: reducción de carga total y reducción de carga mínima de 40%. El primero contempla que el operador de red puede interrumpirle el 100% del flujo de potencia a un nodo controlable si es óptimo para el sistema, mientras que el segundo establece un límite mínimo de reducción de 40% que el DU no puede violar. Se escogió el nodo 75 con potencia instalada de 47 MW. Las Tabla 7. Resultados de simulación con un nodo controlable y reducción total. y Tabla 8. Resultados de simulación con un nodo controlable y reducción mínima del 40%. muestran los resultados de la simulación para el caso de reducción total y el caso de reducción mínima de 40% respectivamente.
Tabla 7. Resultados de simulación con un nodo controlable y reducción total.
| Ítem | Valor simulado |
Reducción |
| 𝐶𝑇𝑜𝑡𝑎𝑙 [$] | 144.146,81 | 4,01% |
| 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 [$] | 145.420,86 | 5,35% |
| 𝐼2𝑍 [MW] | 130.793 | 1,61% |
Tabla 8. Resultados de simulación con un nodo controlable y reducción mínima del 40%.
| Ítem | Valor simulado |
Reducción |
| 𝐶𝑇𝑜𝑡𝑎𝑙 [$] | 148.518,62 | 1,10% |
| 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 [$] | 149.493,30 | 2,70% |
| 𝐼2𝑍 [MW] | 131.196 | 1,31% |
El algoritmo arroja, además, las potencias óptimas que deberían ser despachadas al nodo 75: 18,60 MW y 22,36 MW respectivamente. Es claro notar que una reducción total en la carga interrumpible disminuye los costos totales de generación en mayor medida que lo hace la reducción mínima de 40%. Esto se debe a que, al ser capaz el DU de interrumpir más carga en un nodo, este utiliza esta facultad para usar menos generación propia (pagando más compensación) y así alivianar el estrés del sistema reduciendo las pérdidas activas. Se puede observar que en ambos casos hay una disminución sustancial de las pérdidas activas: 2.138 MW y 1.736 MW para ambos casos.
5.4. Optimización de costos por medio de la inclusión de siete nodos con demanda controlable.
En el anterior numeral se observó el impacto positivo de la inclusión de una carga controlable dentro del sistema de potencia, teniendo en cuenta los criterios de selección planteados en la sección 5.1 dado el resultado anterior, es necesario determinar el comportamiento del sistema al incluir cargas controlables en los nodos con potencial de interrupción. Dentro del algoritmo de simulación DEEPSO se incluyeron los nodos 8, 23, 27, 42, 70, 75 y 90 como cargas controlables, dando al algoritmo dos posibilidades, interrupción total de carga e interrupción parcial de carga (hasta el 60%), con los costos de compensación por bloque de interrupción mencionados en la Tabla 5. Precio de compensación por bloque de carga interrumpida..
5.4.1. Con reducción hasta del 100% de la carga
Se realizó la simulación del sistema sujeto a los costos de compensación de la Tabla 5. Precio de compensación por bloque de carga interrumpida., con 7 nodos bajo la posibilidad de reducir hasta el 100% de la demanda. La Tabla 9. Reducción porcentual de carga demandada en los nodos controlables. muestra el total de carga interrumpida en cada uno de los nodos simulados, y la figura 1 muestra tal información de manera gráfica con respecto a los resultados del caso base presentados en la Tabla 6. Resultados de simulación del caso base. Es claro notar en la Figura 1. Potencia interrumpida, caso reducción del 100%. que el algoritmo busca despachar menos potencia entre más margen de interrupción tenga (100% para este caso) ya que ello mejora el porcentaje de pérdidas y minimiza el costo de generación del sistema. La franja naranja de la Figura 1. Potencia interrumpida, caso reducción del 100%. representa la potencia que dejó de ser despachada y se percibe gráficamente la tendencia de re-despachar menos potencia en todos los nodos interrumpibles que el algoritmo adopta.
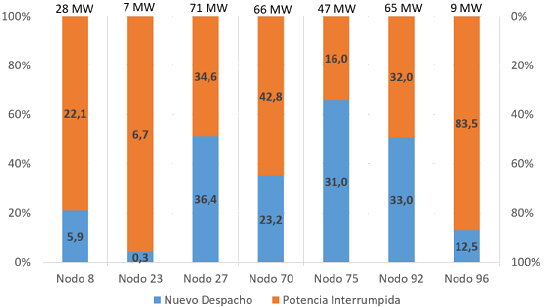
Figura 1. Potencia interrumpida, caso reducción del 100%.
Tabla 9. Reducción porcentual de carga demandada en los nodos controlables.
| Nodo | Demanda Base [MW] |
Demanda Nueva [MW] |
Interrumpido |
| 27 | 71,0 | 36,42 | 48,70% |
| 75 | 47,0 | 31,030 | 33,98% |
| 8 | 28,0 | 5,878 | 79,01% |
| 23 | 7,0 | 0,289 | 95,87% |
| 92 | 65,0 | 32,959 | 49,29% |
| 70 | 66,0 | 23,222 | 64,82% |
| 42 | 96,0 | 12,547 | 86,93% |
Tabla 10. Reducción porcentual de costos y pérdidas por la inclusión de nodos con demanda controlable.
| Ítem | Valor simulado | Reducción |
| 𝐶𝑇𝑜𝑡𝑎𝑙 [$] | 140.208,051 | 6,60% |
| 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 [$] | 140.644,702 | 8,50% |
| 𝐼2𝑍 [MW] | 118.709 | 10,70% |
5.4.2. Con reducción hasta del 60% de la carga
De igual manera que en el caso anterior se realizó la simulación del sistema sujeto a los costos de compensación de la tabla 5, con 7 nodos bajo la posibilidad de reducir hasta el 60% de la demanda. La tabla 11 muestra el total de carga interrumpida en cada uno de los nodos simulados, y la Figura 2. Potencia interrumpida, caso reducción del 60%. muestra la reducción porcentual de costos (𝐶𝑇𝑜𝑡𝑎𝑙 y 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠) y perdidas (𝑰2𝒁) con respecto los resultados del caso base presentados en la tabla 6 (la tabla 11 muestra los datos de la Figura 2. Potencia interrumpida, caso reducción del 60%.). En este caso, el algoritmo actúa re-despachando menos potencia que en el caso de reducción del 100%, lo cual se observa con el tamaño de las franjas azules.
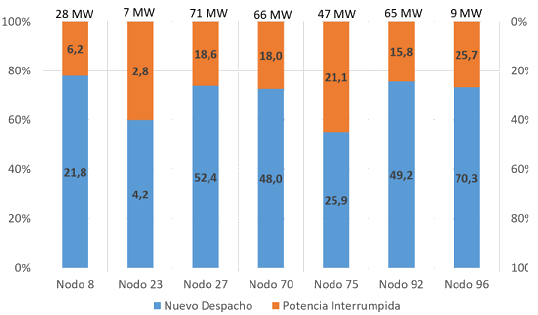
Figura 2. Potencia interrumpida, caso reducción del 60%.
Es fácil establecer que al aumentar el número de nodos con demanda controlable (pasar de 1 solo nodo controlable a 7 nodos) en el sistema se disminuyen los costos y se evidencia una reducción de las pérdidas activas en el sistema. A esto se suma que, si el DU tiene la facultad de interrumpir hasta el 100% de la demanda controlable, el efecto positivo en el sistema es más perceptible y mayor que solo permitir el 60% de la demanda. No obstante, por condiciones operativas de los usuarios asociados a los nodos, permitir una reducción total de la demanda no siempre es beneficioso para ellos, porque esto podría implicar muy altos costos de instalación de una planta de respaldo que supliría su propia demanda. Por tal razón, cada usuario que tiene el potencial de convertirse en un nodo controlable debe realizar un estudio para establecer el porcentaje óptimo de disminución de su demanda en función de su capacidad financiera. De este análisis debe salir una conclusión que arroje luces sobre si ser un nodo controlable es económicamente óptimo o no y es aquí en donde los costos de compensación deben ajustarse para que el análisis financiero sea positivo.
Es por ello que no todas las cargas tienen la capacidad de ser controlables.
Tabla 11. Reducción porcentual de carga demandada en los nodos controlables.
| Nodo | Demanda Base [WM] |
Demanda Nueva [WM] |
Interrumpido |
| 27 | 71,0 | 52,438 | 26,14% |
| 75 | 47,0 | 25,851 | 45,00% |
| 8 | 28,0 | 21,833 | 22,03% |
| 23 | 7,0 | 4,193 | 40,10% |
| 92 | 65,0 | 49,197 | 24,31% |
| 70 | 66,0 | 47,978 | 27,31% |
| 42 | 96,0 | 70,317 | 26,75% |
Tabla 12. Reducción porcentual de costos y pérdidas por la inclusión de nodos con demanda controlable.
| Ítem | Valor simulado |
Reducción |
| 𝐶𝑇𝑜𝑡𝑎𝑙 [$] | 147.932,176 | 1,50% |
| 𝑓𝑓𝑖𝑡𝑛𝑒𝑠𝑠 [$] | 150.501,527 | 2,04% |
| 𝐼2𝑍 [MW] | 123.818 | 6,90% |
6. Conclusiones
Se estableció un criterio para encontrar los nodos con potencial para convertirse en CL por medio del estudio de los costos individuales de cada unidad de generación y el flujo de potencia del sistema. Los nodos de demanda asociados a las líneas con mayor porcentaje de pérdidas fueron considerados para ubicar allí una IL. Del sistema de 118 nodos de la IEEE, los nodos 8, 23, 27, 70, 75, 92 y 96 fueron los nodos con mayor potencial, y por lo tanto, los simulados como IL. Este criterio presentó un mayor grado de asertividad a comparación de una selección aleatoria de nodos, ya que la selección aleatoria puede presentar incluso un impacto negativo en los costos. Esto debido a que no todos los nodos están asociados a las líneas con mayores pérdidas y violación de restricciones del sistema.
Se evidenció el impacto que genera la inclusión de una sola carga controlable en un sistema de potencia, tanto en términos de disminución de pérdidas de energía, como en la disminución del costo total de generación. Se estudiaron dos tipos de carga interrumpible: con reducción total (100% de la demanda) y reducción parcial (hasta 60% de la demanda), asociadas a un costo de compensación estipulado por medio de un estudio de los costos individuales de cada unidad de generación. En el primer caso, se redujo en un 4.01% el costo de generación total y en 1.61% las pérdidas activas, en el segundo caso se redujo en un 1.10% el costo total de generación y en un 1.31% las perdidas. Es claro notar que permitir la reducción total de la demanda favorece en mayor grado la reducción de costos, mientras que la reducción en pérdidas es menos notoria. Dado este resultado, se propuso incluir más CL en el sistema con el fin de validar dichas conclusiones ante un mayor número de demandas controlables.
Se simuló el sistema con los 7 nodos ya mencionados bajo los dos tipos de carga. En el primer caso (reducción total) se disminuyó en 6.60% el costo total de generación y en 10.70% las perdidas activas, mientras que en el segundo la reducción fue de 1.50% y 6.90% respectivamente. De allí se concluye que permitir la reducción total y aumentar el número de cargas genera una mayor reducción tanto en los costos de generación como en las perdidas. Sin embargo, no todos los nodos tienen la capacidad para soportar una reducción total de su demanda, y es por ello que el caso de reducción parcial tiende a ser el caso más real.
7. Referencias bibliográficas
Dean, D., Ortmeyer, T., & Wu, L. (2016). Transportation Modeling and Data Needs for Fast Charging Electric Vehicles. 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC). IEEE. Obtenido de http://ieeexplore.ieee.org/document/7841384/citations https://doi.org/10.1109/esars-itec.2016.7841384 [Link]
Galus, M., Koch, S., & Andersson, G. (2011). Provision of Load Frequency Control by PHEVs, Controllable Loads, and a Cogeneration Unit. IEEE Transactions on Industrial Electronics, 58(10). Obtenido de http://ieeexplore.ieee.org/document/5699360/.https://doi.org/10.1109/tie.2011.2107715 [Link]
International Energy Agency. (2015). Key World Energy Statistics. OECD/IEA. https://doi.org/10.1787/key_energ_stat-2015-en [Link]
Minghong, P., Lian, L., & Chuanwen, J. (2012). A review on the economic dispatch and risk management of the large-scale plug-in electric vehicles (PHEVs)-penetrated power systems. Renewable and Sustainable Energy Reviews, ScienceDirect, 16(3), 1508-1515. Obtenido de http://www.sciencedirect.com/science/article/pii/S1364032111006010 [Link]. https://doi.org/10.1016/j.rser.2011.12.009 [Link]
Pan, X., Li, Y., & Wang, L. (2012). Resarch on Coordinative Optimal Dispatch of Interruptible Load on Multi Time Scale. China International Conference on Electricity Distribution, 386. Obtenido de http://ieeexplore.ieee.org/document/6508563/ [Link]. https://doi.org/10.1109/ciced.2012.6508563 [Link]
Rivera , S., Arevalo, J., & Santos, F. (2018). Uncertainty Cost Functions for Solar Photovoltaic Generation, Wind Energy Generation, and Plug-In Electric Vehicles: Mathematical Expected Value and Verification by Monte Carlo Simulation. International Journal of Power and Energy Conversion, In Press. Obtenido de http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijpec [Link]
Rivera, S., & Romero, A. (2018). Dispatch Modeling Incorporating Maneuver Components, Wind Power and Electric Vehicles Penetration, using Heuristic Techniques. En K. Lee, Application of Modern Heuristic Optimization Techniques in Power and Energy Systems. New York: IEEE.
Ruifeng Shi, Changhao Sun, Zhenyu Zhou, Li Zhang, & Zihang Liang. (2016). A Robust Economic Dispatch of Residential Microgrid with Wind Power and Electric Vehicle Integration. 2016 Chinese Control and Decision Conference (CCDC). Obtenido de http://ieeexplore.ieee.org/document/7531621/ [Link]. https://doi.org/10.1109/ccdc.2016.7531621 [Link]
Shahirinia, A., Soofi , E., & Yu, D. (2016). Probability distributions of outputs of stochastic economic dispatch. Electrical Power and Energy Systems, ScienceDirect, 81, 308–316. Obtenido de http://www.sciencedirect.com/science/article/pii/S0142061516303088 [Link]. https://doi.org/10.1016/j.ijepes.2016.02.043 [Link]
Sharma, I., Bhattacharya, K., & Cañizares, C. (2015). Smart Distribution System Operations With Price-Responsive and Controllable Loads. IEEE Transaction on Smart Grids, 6(2). Obtenido de http://ieeexplore.ieee.org/document/6980127/ [Link]. https://doi.org/10.1109/tsg.2014.2372674 [Link]
Surender Reddy , S., & Bijwe, P. (2015). Real time economic dispatch considering renewable energy resources. Renewable Energy, ScienceDirect, 83, 1215-1226. Obtenido de http://www.sciencedirect.com/science/article/pii/S0960148115300343. https://doi.org/10.1016/j.renene.2015.06.011 [Link]
Xu Wang, Chuanwen Jiang, & Bosong Li. (2016). Active robust optimization for wind integrated power system. Renewable Energy, ScienceDirect, 97, 798-808. Obtenido de http://www.sciencedirect.com/science/article/pii/S0960148116305596. https://doi.org/10.1016/j.renene.2016.06.035 [Link]
Yao, S., Liu, H., Lu, D., & Yuan, X. (2015). Time-Space Characteristic of Interruptible Load on Dispatch Solution. Internacional Federation of Automatic Control, 48(28), 1355-1358. Obtenido de http://www.sciencedirect.com/science/article/pii/S2405896315029444 [Link]. https://doi.org/10.1016/j.ifacol.2015.12.320 [Link]
Yousuf Saber, A., & Kumar Venayagamoorthy, G. (2013). Smart Micro-grid Optimization with Controllable Loads Using Particle Swarm Optimization. 2013 IEEE Power & Energy Society General Meeting. Obtenido de http://ieeexplore.ieee.org/document/6672780/ [Link]. https://doi.org/10.1109/pesmg.2013.6672780 [Link]
Ziadi, Z., Taira, S., Oshiro, M., & Funabashi, T. (2014). Optimal Power Scheduling for Smart Grids Considering Controllable Loads and High Penetration of Photovoltaic Generation. IEEE TRANSACTIONS ON SMART GRID, 5(5). Obtenido de http://ieeexplore.ieee.org/xpl/RecentIssue.jsp?punumber=5165411 [Link]. https://doi.org/10.1109/tsg.2014.2323969 [Link]
* Para los alcances de este trabajo, un PHEV y un EV en modo V2G son lo mismo desde el punto de vista del ED.
1 Ingeniero Electricista, Universidad Nacional de Colombia, Bogotá, Colombia, jusosorioch@unal.edu.co [Link]
2 Ingeniero Electricista, Universidad Nacional de Colombia, Bogotá, Colombia, wfguzmanp@unal.edu.co [Link]
3 Doctor en Ingeniería, Instituto de Energía Eléctrica, Universidad Nacional de San Juan; Postdoctorado Asociado,
Massachusetts Institute of Technology, Cambridge, USA; Profesor, Universidad Nacional de Colombia, Bogotá, Colombia,
srriverar@unal.edu.co [Link]