Andrés Felipe García1, Cristina Gómez2, Tibisay Sánchez3, Alfredo David Redondo4, Leonardo Betancur5, Roberto Carlos Hincapié6
Partiendo de los principios geométricos de Triangulación y Trilateración se presentan algunas técnicas de estimación de ubicación como lo son ToA (Tiempo de llegada), TDoA (Diferencia en Tiempo de llegada) y AoA (Ángulo de llegada). Para estas técnicas de estimación diferentes algoritmos son analizados incluyendo el método Analítico, el método por Mínimos Cuadrados y el método por Series de Taylor para ToA y TDoA y Capon, Bartlett y MUSIC para AoA. Éste artículo pretende presentar una revisión del estado del arte sobre algunas técnicas de estimación de ubicación y su descripción matemáticamente.
Palabras clave: Algoritmos; ToA; TDoA; AoA; ND; NR.
Based on the geometric principles of Triangulation and Trilateration some location estimation techniques such as ToA (Time of Arrival), TDoA (Time Difference of Arrival) and AoA (Angle of Arrival) are presented. For these estimation techniques different algorithms are analyzed including the Analytical method, Least Squares method and Taylor Series method for ToA and TDoA, and Capon, Barttlet and MUSIC for AoA. This article pretends to present survey of location estimation techniques and their mathematical description.
Key words: Algorithms; ToA (Time of Arrival); TDoA (Time Difference of Arrival); AoA (Angle of Arrival); TN (Target Node); RN (Reference Node).
Cuando se mencionan temas como Multilateración, Radiovigilancia o incluso Geolocalización, existen diversas técnicas y algoritmos que giran en tomo a demostrar y estmcturar los principios de funcionamiento y de solución al identificar un objetivo estableciendo diferentes parámetros principalmente las coordenadas de ubicación. En ésta oportunidad se plantean tres técnicas de interés, a nivel de los principios básicos de geolocalización inalámbrica ó radiolocalización, que desarrollan y establecen los principios de estimación de ubicación entre un nodo de destino y una red de nodos de referencia. Estas técnicas ToA (Tiempo de Llegada) y TDoA (Diferencia en Tiempo de llegada) y AoA (Angulo de Llegada) comprenden tanto las coordenadas de referencia como las de destino y un rango de estimación de error que se reduce con base en la cantidad de nodos de referencia de acuerdo a la topología de la red. Esto se debe a que la estimación de rango se podrá ver afectada por el mido y por los componentes multitrayecto, lo que implicará que no siempre exista una intersección en un mismo punto, que es lo que define la ubicación del nodo de destino. Teniendo en cuenta que lo que busca la estimación de ubicación es encontrar las coordenadas más cercanas a la posición actual.
Así mismo, se establecen seis métodos cuyo principio matemático conforma un algoritmo que permite establecer mediante la asignación de variables, una solución a las incógnitas establecidas y de igual forma simular el comportamiento en cada una de las tres técnicas. Estos métodos se clasifican por método Analítico, método de Mínimos cuadrados, método de Series de Taylor, CAPON, MUSIC y Bartlett.
Finalmente se analizan algunos parámetros como el RMSE (root mean square error), el MAE (mean absolute error) y el CDF (cumulative distribution function) sobre las técnicas de estimación de ubicación ToA y TDoA. Técnicas como éstas cuyos métodos se soportan en algoritmos que establecen cierto grado de precisión a nivel de la disminución del rango de estimación del error, se convierten en una base fundamental para desarrollar e implementar nuevos algoritmos híbridos como TDoA/DoA y algunas técnicas más complejas como RiMAX (Engineering, 2004). Es por ello que en la sección 1 hacemos referencia sobre el objetivo de las técnicas de ToA y TDoA; su principio y operación. Más adelante, sobre la sección 2 y 3 nos enfocamos en la sustentación matemática de cada técnica mediante algoritmos como el Analítico, Mínimos cuadrados y Series de Taylor. Así mismo concluimos ambas secciones con un análisis de desempeño. Para la sección 4, nos referimos al principio y operación que contiene la técnica de AoA recreando una introducción hacía el principio matemático que la establece y dando pie a las demás secciones donde se relacionan otros algoritmos como CAPON, Bartlett y MUSIC. Concluyendo así con la sección de conclusiones, referentes a cada técnica y algoritmo en tomo a un escenario donde se plantea una red de nodos de referencia y de destino.
La estimación del tiempo de llegada ToA por sus siglas en inglés (Time of Arrival) es una técnica de posi-cionamiento que permite medir la distancia, estableciendo así la ubicación. En éste escenario se plantean múltiples nodos de referencia (NR) que en sincronía permiten hallar un nodo de destino (ND) vía triangulación de acuerdo a (Vossiek, et al. 2003). La localización del ND es posible asumiendo que todas las coordenadas de los nodos de referencia son conocidas. Asumiendo un escenario coplanar, donde las posiciones de los NR son conocidas, sólo tres NRy tres mediciones de distancias (ToA) bastarán para localizar el ND. Pero al tener un escenario no-coplanar, se requerirán de cuatro NR. Usando la medida de distancia, la posición del ND se localiza dentro de una esfera de radio Ri con el receptor i en el centro de la esfera (aquí Ri es directamente proporcional al TOA τi.
La localización del ND es posible establecerla ya sea a través de los NR estableciendo una estación base de referencia, o mediante el propio ND según (Zekavat, etal,. 2012).
Sin embargo, ToA al ser una técnica robusta, posee algunos inconvenientes según (Rappaport, et al,.1996):
Requiere de todos los nodos (tanto los NR como los ND) para tener una sincronización precisa. Es decir, un pequeño error en temporización puede generar un gran error en el cálculo de la distancia Ri.
La señal transmitida debe “etiquetarse” con un “sello de tiempo” (Time stamp) con el fin de permitir que los NR determinen el instante en el que inició la señal en el ND. Este sello de tiempo adicional incrementa la complej idad de la señal transmitida y puede conducir hacía una fuente adicional de error.
Adicionalmente, con base en (ITU, 2011) otro inconveniente que presenta este método es que a menos que se conozcan las características de la señal de modo que le permita al receptor determinar con precisión el tiempo de llegada bajo condiciones de canal pobres, éste método requerirá de altas relaciones señal a ruido (SRN), alta relación señal a interferencia, distorsión multitrayecto limitada en todos los receptores. Así mismo la exactitud del método es posible mejorarlo utilizando información conocida a partir de señales moduladas digitalmente.
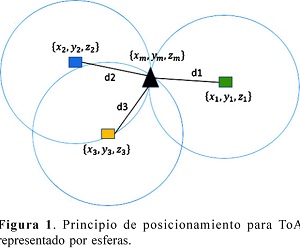
De igual forma como lo establece (Reza, 2000) la posición del móvil, en este caso el ND, podrá determinarse con precisión si existe una completa línea de vista (LOS) entre la estación móvil o ND y las demás estaciones base o NRs. Sin embargo, la ocurrencia de no tener línea de vista (NLOS) de propagación generará que la señal tome un trayecto más largo en dirección hacia el receptor del NR y el ToA medido es generalmente mayor que el tiempo de llegada de una señal con LOS. En la Figura 1 a continuación se visualiza el principio de posicionamien-to de ToA.
A diferencia de ToA, TDoA aborda primero el inconveniente que se presenta, eliminando el requisito de sincronizar el reloj del ND con relojes de los NR. En TDoA todos los NR reciben la misma señal transmitida mediante el ND. Por lo tanto, siempre y cuando los relojes de los NR estén sincronizados, el error en el tiempo de llegada en cada NR debido a la no-sincronización de los relojes es el mismo. En la Figura 2 a continuación se visualiza el principio de posicionamiento de TDoA.
Así como lo establece (Zekavat, et al,. 2012) la estimación en la Diferencia del Tiempo de Llegada requiere la medición de la diferencia en el tiempo entre las señales entrantes hacía dos NR. Al igual que en ToA, éste método asume que las posiciones de los NR son conocidas. Y geométricamente puede representarse mediante hipérbolas. Una hipérbola es aquel lugar geométrico de un punto en un plano tal que la diferencia de las distancias de dos puntos fijos (llamados focos) es una constante. Asumiendo entonces un escenario coplanar, donde hay tres NR y sus coordenadas son conocidas y dos mediciones TDoA bastarán para localizar un ND. Teniendo en cuenta que la estación base de referencia de toda la red de nodos observadores, será aquella que reciba primero la señal del ND. Ya que todas las mediciones a partir de ésta técnica se harán respecto a la estación base de referencia. En un escenario no-coplanar, las posiciones de los cuatro NR y las tres mediciones TDoA son requeridas.
En ToA el punto de intersección de todas las esferas podrá determinar la posición del nodo de destino, ya que los centros serán las coordenadas de los nodos de referencia y de los rangos correspondientes entre los nodos de referencia y el nodo de destino de acuerdo a (Shen, et al,.2008), que a su vez serán denominados como los radios. Los nodos de referencia podrán representarse mediante la ecuación de la esfera como se muestra a continuación:
Donde las variables (xi, yi, zi) son las coordenadas conocidas para los nodos de referencia y la variable mi (i = 1,2, ...n) son las estimaciones de rango. El número de nodos de referencia se establece con la variable n. Variables como (x, y, z) son las coordenadas del nodo de destino.
La precisión de la estimación de rango durante la simulación y la medición en campo se verá afectada por el ruido y los componentes multitrayecto, de esta forma no se garantizará que las esferas se intersecten en un mismo punto. Con base en lo anterior el objetivo de la estimación de ubicación será entonces encontrar la mayor precisión de las coordenadas más cercanas a la posición actual.
Según (Caffery, et al,. 1998), (Cheung, et al,. 2004) y (Yu, et al,. 2005) la posición del nodo de destino podrá ser determinada al resolver las ecuaciones no lineales directamente. El número de ecuaciones para el sistema podrá ser determinado al número de nodos de referencia que se planteen en la red, i.e., si el sistema posee solo tres nodos de referencia, el sistema tendrá un conjunto de tres ecuaciones con tres incógnitas tal como se muestra a continuación:
Basado en estos parámetros es posible establecer la primera ecuación para el procedimiento matemático a partir de la ecuación (1), es decir, se tomará la ecuación (1) como partida y se sustituirá el primer uno cuando i=1 y así sucesivamente a partir de éste cuando i valga 2,3,.. .n (i= 2,3), de esta forma se irá formando la matriz a partir de un sistema de ecuaciones lineales como se muestra en la ecuación 4 a continuación:
Posteriormente se establecen los cambios de variables para conformar los grupos de ecuaciones que nos llevaran a estructurar la matriz inicial bajo el modelo de la ecuación:
Las ecuaciones (5), (6) y (7) conforman el primer grupo de ecuaciones para estructurar la matriz:
Las ecuaciones (8), (9) y (10) conforman el segundo grupo de ecuaciones:
Finalmente después de desarrollar las diferentes ecuaciones en los grupos anteriores obtenemos el sistema de ecuaciones lineales en (11):
En éste sistema tenemos dos ecuaciones con tres incógnitas. Luego, una de las incógnitas (x’) será un parámetro, para las otras dos variables (y’ e z’) que a su vez estará en términos de funciones para estas dos bajo la ecuación (12):
Luego tendremos (12) en (1) para cuando i=1, formando así una ecuación cuadrática:
Considerando las ecuaciones (12) y (2) encontraremos la solución ax’ como las coordenadas del nodo de destino.
Para la ecuación (13) tenemos tres posibilidades al resolver esta ecuación cuadrática:
Este escenario asumido en un sistema sobre determinado con más de tres ecuaciones en (1). Para encontrar la ubicación estimada, podemos usar este método (el método de combinación analítica). La idea principal es resolver las combinaciones de la ecuación incluyendo tres ecuaciones. La estimación de ubicación final se obtendrá mediante el promedio de todos los resultados según (Shen, et al,. 2008).
En este método podremos obtener el mismo principio al que comprende el método analítico pero con una situación y variables diferente.
Para la ecuación (14) cuando i=1 este será el enfoque principal para el desarrollo de las incógnitas. Basado en la ecuación inicial en ToA será posible establecer las siguientes ecuaciones:
Una vez que se han desarrollado las ecuaciones (15),(16)y(17) conformamos la matriz de ecuaciones lineales como se observa en (18)
Nosotros tendremos una respuesta con la ecuación (18) mediante el uso del método de mínimos cuadrados.
En primer lugar se define una función como el parámetro inicial. La variable es la estimación ToA en el nodo de referencia, i y εi es el rango de estimación de error según afirman (Yu, et al,. 2006) y (Foy, 1976).
Considerando los parámetros iniciales tenemos
Las variables δx, δy, y δz son los errores de estimación de ubicación a ser determinados. Si (23) se expande en
la serie de Taylor y se retienen los primeros dos términos se produce:
Donde,
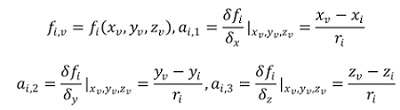
En el cual,
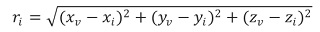
Reescribimos (25) como
Donde,
La estimación de peso de mínimos cuadrados de (26) es:
A partir de la posición inicial suponemos Xv, Yv, Zv y δ computada desde (27), la estimación de ubicación puede actualizarse acorde a:
La estimación de ubicación puede ser definida continuamente mediante el procedimiento anterior.
Considerando los parámetros iniciales con ToA y de acuerdo con (Nur-a-alam, al,. 2008) podremos medir con respecto al primer nodo de referencia,
Donde son mi,1 (i=2, 3,..., n) las estimaciones de rango. La variable ri (i= 1, 2,..., n) son los parámetros desconocidos de las distancias reales entre el nodo de referencia y el nodo de destino. La variable n es el número de NR. Las coordenadas conocidas serán Xi, Yi, Zi para el NR. Las coordenadas del ND estarán determinadas como (x,y,z). Así, la ecuación (1) puede ser reescrita como:
Donde hay cuatro incógnitas, x,y,z y r1.
Para este método el mínimo número de NR son cuatro porque hay cuatro incógnitas, (x,y,z) y r1, en (30). Al sustituir las ecuaciones (2) y (3) teniendo valores para (i=2,3,4) incluyendo en (30) y restando el primero cuando i=1 y desde éste para i=2,3,4 resultará en un conjunto de ecuaciones de acuerdo al número deNR y en forma de matriz como se visualiza en (32):
Teniendo en cuenta el planteamiento anterior se selecciona una la de las incógnitas ri como un parámetro, y las otras tres como funciones de ésta. Acoplando la ecuación (33) se obtendrá una ecuación cuadrática en términos de r¡. Dicha solución conlleva a conocer las coordenadas del ND. Es posible entonces implementar este método para un sistema sobre determinado de ecuaciones con combinaciones de cuatro incógnitas como lo establece (Sayed, 2005).
En este método se conforma un sistema de ecuaciones lineales resultado de restar la primera posición i=l de otras ecuaciones como (30)
Las variables (X' Y', Z') corresponden a las coordenadas desconocidas del ND y las variables (X'i Y'i, Z'i) a las coordenadas de los NR y que son definidas en (2) y (3) así como (31)
Donde se define en (21) y
La solución de mínimos cuadrados se genera en
Posteriormente ésta solución contendrá un parámetro r1 que formará una ecuación cuadrática. La solución de r1 entregará el resultado final.
Al igual que en ToA el principio para este método se mantiene pero la función se define como:
En este caso la variable m1 + 11 es la estimación del (i+1)th nodo de referencia con el primer uno y ε1 + 11es la diferencia en el rango correspondiente al error de estimación con la matriz de covarianza Q.
Incluyendo (40) en Series de Taylor usando una estimación inicial Xv, Yv, Zv y reteniendo el primero de dos términos se genera,
Cuyas variables δx, δy, δz, corresponden a los errores de estimación de ubicación que se determinan mediante,
Es posible plantearlo como en (23) pero donde,
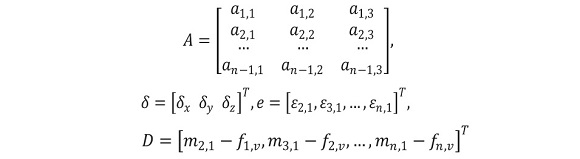
Se deberá tener en cuenta que el peso del estimador de mínimos cuadrados de éste se plantea como en (27). Y al igual que en ToA, se computa 5 con (27) a través de una supuesta posición inicial, actualizando la estimación de ubicación acorde a (28).
De acuerdo con (Shen, 2012), (Guvenc, 2008) y (J. Huang, et, al,. 2012) diferentes simulaciones han permitido medir el rendimiento de los algoritmos basados en ToA y TDoAy se ha establecido que:
Siguiendo el modelo matemático presentado en (Gross, 2005), (Trees, 2002) y (Zhou, Q., eta/,. 2014); la estimación de Angulo de Llegada (Angle of Arrival - AoA) se ha conocido también como estimación espectral, estimación de Dirección de Llegada (Direction of Arrival - DoA) o Bearing Estimation. Algunas referencias relacionan la estimación espectral como la habilidad para seleccionar varios componentes de frecuencias fuera de un conjunto de señales. Este concepto fue expandido para incluir los problemas de frecuencia, número de onda y después la estimación AoA. El “bearing estimation” es un término más usado comúnmente entre la comunidad científica, específicamente en la comunidad de SONAR y es estimación AoA para aplicación en problemas de acústica.
Algunos de los algoritmos para AoA se basan en la matriz de correlación. Cobra importancia conocer un poco la descripción del arreglo, la señal recibida, y la adición de ruido. En la figura 1 se puede observar la representación de una matriz en recepción de ondas planas incidentes desde varias direcciones.
En la figura 1 se muestra D señales de llegada a partir de D direcciones. Estas señales son recibidas por una matriz de M elementos con M pesos potenciales. Cada señal recibida Xm(k) incluye una adición de cero ruido Gaussiano. El tiempo está representado mediante la kth muestras de tiempo. Así, el arreglo de saliday puede ser generado de la siguiente forma:
Donde,
Y
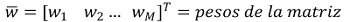
Por lo tanto, cada una de las señales complejas D llega en ángulos θi y es interceptada a partir de M elementos de antena. Asumiendo que las señales entrantes son monocromáticas y el número de señales que llegan D < M. Es entendible que las señales que llegan son variables en el tiempo y por lo tanto los cálculos se basan en las instantáneas de tiempo de la señal entrante. Así mismo, si los transmisores están en movimiento la matriz de los vectores de dirección está cambiando con el tiempo y los ángulos de llegada correspondientes están cambiando.
La matriz MxM de correlación R̄xx se relaciona bajo la siguiente estructura como:
La matriz arreglo de correlación R̄xx y la matriz fuente de correlación se encuentran a partir del valor esperado o de los respectivos valores absoluto cuadrado (i.e., R̄xx = E[x̄. x̄H] yR̄ss = [s̄.s̄H]).
Cuando las señales no están correlacionadas, obviamente tiene que ser una matriz diagonal porque los elementos fuera de la diagonal tienen no correlación. Cuando los elementos son parcialmente correlacionados, R̄ss es no singular. Cuando las señales son coherentes, R̄ss se vuelve singular porque las filas son combinaciones lineales una a la otra según (Stoica, et al,. 1997). La matriz de vectores de dirección, Ā, es una matriz MxD donde las columnas son independientes según afirma (Shan, et 1985) y (Minasyan, 1994). A menudo en la literatura la matriz de correlación también se encontrará como la matriz de covarianza. Y esto será cierto si los valores de las señales y el ruido son cero. En dicho caso, las matrices de covarianza y correlación serán idénticas. El valor medio de la señal que llega debe ser necesariamente cero porque las antenas no pueden recibir señales en DC. El ruido inherente en el receptor puede o no tener una medida de cero dependiendo de la fuente del ruido del receptor. Habrá mucha información útil para descubrirse en el análisis propio en el arreglo de la matriz de correlación, por lo que los detalles de la estructura propia se describen en (Godara, 1997).
El objetivo de las técnicas de estimación de AoA es definir una función que entregue una indicación de los ángulos de llegada basados en máximos vs ángulos. Ésta función es tradicionalmente llamada el pseudoespectro P(θ) y las unidades pueden ser en energía o en vatios (o en tiempos de energía o vatios al cuadrado). Existen varios enfoques para definir el pseudoespectro a través de la formación de haz (beamforming), el arreglo de la matriz de correlación, análisis propio, predicción lineal, varianza mínima, máxima probabilidad, MUSIC, root-MUSIC entre otros que se pueden analizar más al detalle en (Trees, 2002) y (Stoica, 1997). Es por ello que a continuación se plantean algunas soluciones pseudoespectrales.
De acuerdo a (Bartlett, 1961) y (Gross, 2005) la estimación AoA basada en ésta técnica es posible definirla como:
La estimación Bartlett AoA es la versión espacial de un periodograma programado y es una estimación beamforming AoA. Bajo las condiciones donde S representa señales monocromáticas no correlacionadas la ecuación (45) es el equivalente para la siguiente expresión:
El periodograma es por lo tanto equivalente a la transformada espacial finita de Fourier de todas las señales que llegan. También es equivalente a la adición de todos los factores de la matriz para cada ángulo de llegada y encontrar el valor cuadrado absoluto.
La estimación CAPON AoA es conocida como la respuesta sin distorsión de varianza mínima ( variance distortionless response - MVDR). También es alternativamente una estimación de máxima verosimilitud de la potencia entrante a partir de una dirección mientras todas las otras fuentes son consideradas como interferencia. Así el objetivo se enfoque en maximizar la relación señal-interferencia (SIR) mientras que pasa la señal de interés no distorsionada en fase y amplitud. Así la matriz fuente de correlación Rss se asume para ser diagonal de acuerdo a (Capon, 1969). Esta SIR maximizada se logra con un conjunto de pesos de la matriz cuando w̄= [w1 w2... wm]τ como se muestra en la figura 1 donde los pesos de la matriz son dados por:
Donde R̄xx es la matriz de arreglos no ponderado. Luego sustituyendo los pesos de la ecuación (47) en la matriz de la figura 1, es posible que luego el pseudoespectro sea entregado por: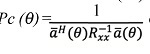 
de acuerdo con (Gross, 2005).
Así mismo en (Gross, 2005) se establece a MUSIC como un acrónimo que relaciona Clasificación Múltiple de Señales. Este enfoque fue establecido por primera vez por (Schmidt, 1986) y es un método popular de estructura propia de alta resolución. MUSIC es un método que promete proporcionar estimaciones imparciales del número de señales, los ángulos de llegada y los puntos fuertes de las formas de onda. El método hace la suposición de que el ruido en cada canal no está correlacionado y construye la matriz de correlación de ruido en diagonal. Las señales incidentes pueden ser algo correlacionadas creando una matriz de correlación de señal no diagonal. Sin embargo, bajo la alta correlación de señal del algoritmo MUSIC, se rompe, y otros métodos deben ser implementados para corregir esta debilidad.
Es importante conocer de antemano el número de señales entrantes donde deberán buscarse los valores propios para determinar el número de señales de entrada. Si el número de señales es D el número de valores propios de señal y de vectores propios es D, y el número de valores propios de ruido y vectores propios es M-D (M es el número de elementos de arreglos). Porque MUSIC explota el subespacio de un vector propio de ruido, lo que se refiere a veces como un método de subespacio.
Para calcular el arreglo de la matriz de correlación asumiendo ruido sin correlación con varianzas iguales se plantea la siguiente ecuación:
Podemos encontrar los valores propios y los vectores propios para R̄xx. Luego se producen D vectores propios asociados con las señales y M-D vectores propios asociados con el ruido. Posteriormente seleccionamos los vectores propios asociados con los valores propios más pequeños. Para señales sin correlación, los valores propios más pequeños son iguales a la varianza del ruido. Luego podemos entonces construir el Mx (M-D) sub espacio dimensional abarcado a partir del ruido de los vectores propios tal como:
Los vectores propios de subespacio de ruido son ortogonales para el arreglo de los vectores dirección en los ángulos de llegada θ1, θ2, ..., θD. Porque de esa condición de ortogonalinidad, es posible mostrar que la distancia Euclidiana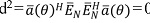 
para cada una y todos los ángulos de llegada θ1, θ2, ..., θD. Colocando así la expresión distancia en el denominador crea picos agudos en los ángulos de llegada. El pseudoespectro MUSIC se entrega como:
De acuerdo con (Redondo, et 2015) la técnica de Capon posee mayor resolución que la de Bartlett, sin embargo si las señales fuente se correlacionan, su rendimiento sufrirá una degradación severa y bajo ese escenario es preferible utilizar Bartlett. Así mismo MUSIC es un método muy popular debido a su estructura propia de alta resolución.
Diferentes métodos y algoritmos basados en ToA, TDoA y AoA se relacionaron en el artículo, con el objetivo de dar a conocer como están estructurados matemáticamente y bajo qué condiciones se establece cada una de sus variables de acuerdo a la topología de la red de nodos.
Se concluye a partir de los diferentes métodos que al igual que las técnicas de AoA, los algoritmos basados en rango como ToA y TDoA también poseen una muy buena precisión debido a una alta resolución.
Si bien la posición del nodo de destino está determinada a la intersección de las esferas formadas por los nodos de referencia, se debe tener en cuenta que esta intersección no siempre se llevará a cabo con tal precisión, debido a que factores externos como el ruido y los componentes multitrayecto afectarán dicha precisión y las esferas no siempre se intersectarán en un mismo punto. Lo que determina entonces que el objetivo de la estimación de ubicación es encontrar las coordenadas más cercanas a la posición actual.
De igual forma se concluye que el rendimiento de los algoritmos dependerá en su momento, de la topología de la red y de la posición del nodo de destino.
Bartleet, M., 1961. Introduction to Stochastic Processes with Special References to Methods and Applications. 3. Edition. Cambridge-London-New York-Melbourne. Cambridge University Press. Volume 59, Issue 7, p. 334.
Bureau, I., 2011. Spectrum monitoring handbook. Switzerland, Geneva. 678 pp.
Caffery, J.. J. & Stuber, G.L., 1998. Subscriber location in CDMA cellular networks. IEEE Transactions on Vehicular Technology, 47(2), pp. 406-416.
Capon, J., 1969. High-Resolution Frequency-Wavenumber Spectrum Analysis. In IEEE, pp. 1408-1418.
Cheung, K.W., So, H.C. & Chan, Y.T., 2004. Least Squares Algorithms for Time-of-Arrival-based Mobile Location. 52(4), pp.1121-1128.
Engineering, M., 2004. COST 273 TD ( 04 ) 045 RI-MAX - A Flexible Algorithm for Channel Parameter Estimation from Channel Sounding Measurements I. Introduction.
Foy, W.H., 2007. Position-Location Solutions by Taylor-Series Estimation. March 1976, pp. 187-194.
Godara, L., 1997. Applications of Antenna Arrays to Mobile Communications. In Part II: Beamforming and Direction-of-Arrival Considerations. Proceedings of the IEEE, pp. 1195-1245.
Gross, F.B., 2005. Smart Antennas for Wireless Communication. In p. 288.
Guvenc, I., Gezici, S. & Sahinoglu, Z., 2008. Ultra-wideband range estimation: Theoretical limits and practical algorithms. Proceeedings of The 2008 IEEE International Conference on Ultra-Wideband, ICUWB 2008, 3, pp. 93-96.
Huang, J. & Wan, Q., 2012. Analysis of TDOA and TDOA/SS based geolocation techniques in a non-line-of-sight environment. Journal of Communications and Networks, 14(5), pp.533-539. Available at: http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=6360052.
M. Vossiek, L. Wiebking, P. Gulden, J. Wieghardt, C. Hoffmann, and P.H., 2003. Wireless local positioning. Microwave Magazine, IEEE (Volume:4, Issue: 4 ), pp. 77-86.
Minasyan, G., 1994. Application of High Resolution Methods to Underwater Data Processing. N.N Andreyev Acoustics Institute.
Nur-a-alam, M. & Haque, M.M., 2008. A Least Square Approach for TDOA / AOA Wireless Location in WCDMA System., (Iccit), pp.25-27.
Oppermann, K.Y. and I., 2005. UWB Theory and Applications, Chichester, UK: Jhon Wiley & Sons, Ltda.
Redondo, A.D. et al., 2015. MIMO SDR-based Implementation of AoA Algorithms for Radio Direction Finding in Spectrum Sensing Activities. (2).
Reza, R., 2000. Data fusion for improved TOA/TDOA position determination in wireless systems. Electrical Engineering, (July). Available at: http://scholar.lib. vt.edu/theses/available/etd-08242000-15320007/.
Sayed, A.H, Tarighat, A.?; Khajehnouri, N., 2005. Network-based wireless location: challenges faced in developing techniques for accurate wireless location information., pp.24-40.
Schmidt, R., 1986. Multiple Emitter Location and Signal Parameter Estimation. IEEE Transactions on Antenna. Propogation, AP-34 No.2, pp. 276-280.
Shan, T.J, M. Wax, T.K., 1985. Spatial Smoothing for Direction-of-Arrival Estimation of Coherent Signals. IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-33, pp. 806-811.
Shen, G, Zetik, R. & Thomá, R.S., 2008. Performance comparison of TOA and TDOA based location estimation algorithms in LOS environment. 5th Workshop on Positioning, Navigation and Communication 2008, WPNC’08, 2008, pp. 71-78.
Shen, M.S.G., 2012. Localization of Active Nodes within Distributed Ultra-Wideband Sensor Networks in Multipath Environments.
Stoica, R, R.M., 1997. Introduction to Spectral Analysis, New York City, USA: Prentice Hall.
T. S. Rappaport, J. H. Reed, and B.D.W., 1996. Position location using wireless communications on highways of the future. IEEE Communication Magazine, pp. 33-41.
Van Trees, H., 2002. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory. In Wiley Interscience.
Yu, K. et al., 2006. UWB location and tracking for wireless embedded networks. Signal Processing, 86, pp. 2153-2171.
Zekavat, S. a R. & Buehrer, R.M., HANDBOOK OPPOSITION LOCATION: Theory, Practice, and Advances.
Zhou, Q. & Duan, Z., 2014. Weighted Intersections of Bearing Lines for AOA Based Localization. Information Fusion (FUSION), 2014 17th International Conference on, (Ml), pp.1-8.
