
Faiber Ignacio Robayo B.1, Ana Maria Barrera F.2 y Laura Camila Polanco C.3
Recibido: 11 Agosto 2015
Aceptado: 30 Octubre 2015
Este artículo presenta el desarrollo de un control neuronal basado en el modelo inverso para el sistema hidráulico multivariable de nivel y caudal de la Universidad Surcolombiana. Con este propósito, se evalúa el grado de acoplamiento entre las variables a controlar a través del método de la matriz de ganancias relativas (RGA), se realiza el modelamiento del sistema y se implementan los controladores en MatLab haciendo uso del Neural Network Toolbox y de Simulink como interfaz de monitoreo y control. El rendimiento del control es evaluado mediante simulaciones y pruebas en tiempo real. La comparación del desempeño del control neuronal frente al control difuso se realiza evaluando tres parámetros: sobreimpulso, error en estado estacionario y tiempo de establecimiento. Los resultados obtenidos demuestran un mejor desempeño frente al controlador fuzzy desarrollado previamente para el mismo sistema. Se evidencia que el error en estado estacionario disminuye notablemente dado que el porcentaje de error máximo es de 0.01% y 0.003% por redes neuronales y de 3% y 1.75% por control difuso, para nivel y caudal respectivamente. En cuanto al sobreimpulso, aunque en el control difuso es mínimo, el control por redes neuronales lo elimina en las dos variables controladas. Para el tiempo de establecimiento se observa que el control neuronal también mejora considerablemente para las dos variables.
Palabras clave: Control Neuronal; sistema MIMO; modelo inverso; MatLab; Simulink; Sistema hidráulico.
This paper presents the development of a neural control based on the inverse model for multivariable hydraulics system of level and flow of Surcolombiana University. The degree of coupling between the control variables is evaluated through the method of relative gain matrix. The system modeling is done and the drivers are implemented in MatLab using the Toolbox and Neural Network Simulink as interface monitoring and control. The control performance is evaluated through simulations and real-time testing. The comparison of performance between the neuronal control and the fuzzy control is done, evaluating three parameters: overshoot, steady-state error and settling time. The results show a better performance against the previously developed fuzzy controller for the same system. It is evident that the steady-state error decreases significantly as the percentage of maximum error is 0.01% and 0.003% by neural networks and 3% and 1.75% by fuzzy control for level and flow respectively. As to overshoot although the fuzzy control is minimal, the control neural networks remove it entirely. For the settling time it is observed that the neuronal control also improves considerably for the two variables.
Key words: Neural Control; MIMO system; inverse model; MatLab; Simulink; Hydraulic system.
En los últimos años, con el acelerado crecimiento de la industria, los procesos han alcanzado un alto grado de complejidad debido a su no linealidad y a que presentan más de un lazo de control, por lo que se ha despertado cierto interés en el uso de diferentes métodos inteligentes que sean capaces de ejercer controles óptimos. Estos procesos conocidos como “Multivariables” pretenden el control de más de una variable como por ejemplo nivel y caudal en el caso de los sistemas de tanques acoplados. El análisis y la aplicación de algoritmos de control adaptativo fueron empleados en un sistema multivariable de tanques interconectados usando como prototipo un modelo simulado de planta instrumentada (Recalde y Burbano, 2006), sin embargo, la aplicación en tiempo real usando Matlab no presentó un buen desempeño. Un trabajo similar empleando control predictivo en un sistema acoplado de dos tanques mediante interfaz de Matlab fue desarrollado concluyendo que se logra disminuir los costos de inversión en hardware pero con un alto costo computacional (Moromenacho, etal., 2010). También se ha trabajado en sistemas acoplados más complejos como es el caso del ajuste, configuración y control de cuatro tanques acoplados en el cual se diseña un control multivariable descentralizado con dos PI, controlando el nivel de dos depósitos mediante la tensión de dos bombas que alimentan a los tanques bajo control; logrando un buen seguimiento de referencias y reducen las interacciones entre lazos (Castelo, etal., 2009).
Los sistemas por redes neuronales son una de las técnicas que desde los años 90 toman importancia por el intento de diseñar controladores inteligentes (Ponce, 2010). Las redes neuronales artificiales se caracterizan por su habilidad de aprender de los ejemplos en lugar de tener que programarse en un sentido convencional. Su uso posibilita que la dinámica de los sistemas complejos sea modelada y un control preciso sea logrado a través del entrenamiento, sin tener información a priori sobre los parámetros del sistema (Parker, 1995). El control de nivel de un tanque a través de redes neuronales, utilizando el Control Directo por Modelo Inverso y el Control Feedforward es realizado y se llega a la conclusión de que en el controlador en Feedforward la variable nivel alcanza el valor de referencia, tiene menos oscilaciones y el tiempo de estabilización es menor que en el Control Directo (Garrido, et al., 2009). Siguiendo por la misma línea, encontramos un trabajo donde se desarrolla una función con redes neuronales basada en modo deslizante para el control de un sistema de tanques acoplados; los resultados muestran que se logra el adecuado control de los tanques, sin embargo, sólo se hizo mediante simulación, no se implementa (Aliasghary, etal., 2011). Dos diferentes enfoques en un sistema de control de dos tanques usando redes neuronales son probados, los enfoques son el NARMA-L2 y el Modelo de Referencia, con resultados que permitieron comparar estos enfoques con los resultados del clásico PID (Majstorovic, et al., 2008). Un sistema adaptativo Neuro-Fuzzy de control para un modelo hidráulico de dos tanques es implementado concluyendo que tan solo un básico conocimiento de la dinámica del sistema es necesaria para el proceso de diseño y que el algoritmo de control muestra un adecuado desempeño (Torres y Anzures, 2013). El diseño de un controlador basado en redes neuronales basado en algoritmos genéticos con optimización multiobjetivo es implementado en un prototipo de sistema de tanques, mostrando un buen desempeño de control (Vassiljeva, etal., 2014). El enfoque de control basado en redes neuronales para un sistema acoplado de tanques es usado, en este sistema se experimenta con un híbrido entre redes neuronales y control PID clásico, sin embargo, los resultados mostrados son solamente a nivel de simulación y el impacto de su desempeño es evaluado en términos del rechazo ante perturbaciones y del seguimiento de la referencia (Ramli, et al., 2009).
De esa manera se observa la tendencia a comparar el desempeño de diferentes tipos de control sobre este tipo de sistemas, así por ejemplo, se describe la aplicación de las teorías de control inteligente para el control de nivel de un sistema multitanque de la marca Inteco (Armijos y Chicaiza, 2011). Los controles implementados son lógica difusa y redes neuronales, concluyendo que el controlador fuzzy cumple con los objetivos mantener los niveles deseados pero las ganancias del error y error acumulado afectan directamente el controlador; sobre el controlador neuronal concluyendo que el mejor desempeño lo muestra el controlador con red neuronal inversa.
La Universidad Surcolombiana actualmente cuenta con sistema de tanques acoplados sobre el cual se pretende el desarrollo del diseño e implementación de un controlador basado en redes neuronales para el sistema hidráulico MIMO (Multiple Input Multiple Output) de nivel y caudal. Estos resultados serán comparados con los obtenidos en la misma planta mediante la técnica de control fuzzy y se pretende comparar sus desempeños para contribuir en el área del control de nivel en procesos, dado que en la región no se tiene evidencia de trabajos con esta técnica de control en este tipo de sistemas tan comunes en la industria.
El contenido de este artículo se organiza de la siguiente forma. En la sección 2 se describen los componentes y variables del proceso, luego se evalúa la interacción entre los lazos del sistema utilizando el método de ganancias relativas (Bristol, 1996), que resulta en la simplificación del sistema en dos subsistemas SISÓ (Simple Input Simple Output) independientes que son identificados a través del System Identification toolbox de MatLab® (Osorio, 2015). Para cada subsistema se implementa un controlador neuronal basado en el modelo inverso (Dreyfus, 2005). En la sección 3 se muestran los resultados obtenidos y se compara el desempeño con un controlador fuzzy (Ramírez y Calvache, 2013) aplicado a este mismo sistema. Las conclusiones se presentan en la sección 4.
En la Figura 1. se muestra el esquema de la planta, la cual consta de tres tanques; tanque de perturbación de nivel TI, tanque principal T2, tanque de reserva T3, dos electroválvulas proporcionales; electroválvula de perturbación Y1, electroválvula de control V2 y una bomba sumergible B1, un sensor de nivel S1 ubicado en la parte superior de T2 y un sensor de caudal S2 ubicado en la tubería inmediatamente después de V2. Se pretende controlar el nivel y el caudal de salida de T2 accionando B1 y V2 que proporcionan el flujo de entrada y salida de líquido de T2 respectivamente. A través de VI se ingresa un flujo de líquido proveniente de TI con el cual se busca perturbar el proceso de control del nivel.
La Figura 2 muestra el diagrama de bloques del sistema, con la discriminación detallada de las etapas empleadas para la adquisición de las señales del sistema, su procesamiento y salida de las mismas hacia la planta.
La descripción de la funcionalidad de estos bloques es mostrada en las siguientes secciones, aunque no de manera detallada, pue nuestro objetivo son los resultados de desempeño del controlador obtenidos.
En esta primera etapa es necesario recolectar los datos que describen correctamente el comportamiento real del sistema, pues de esto depende el desarrollo satisfactorio de las etapas siguientes y en consecuencia un control óptimo para el sistema.
Para hacer la adquisición de datos se ha creado un archivo en simulink, Figura 3, en el que se incorpora la comunicación serial entre la tarjeta de desarrollo Arduino Mega y el computador, además se realizan los cálculos necesarios para convertir las señales de voltaje de nivel y caudal a nivel (cm) y caudal (L/min) respectivamente.
Se decide usar la modulación por ancho de pulso (PWM) para proporcionar los voltajes de control a los actuadores, ya que mejora el rendimiento del sistema al controlar la cantidad de potencia entregada a la carga sin que haya pérdidas considerables de energía ni calentamiento de los artefactos, además permite una máxima variación del ciclo útil del 0% al 100%.
Se consideran como entradas del proceso el voltaje aplicado a la bomba sumergible B1 (VB) y el voltaje aplicado a la electroválvula V2 (VV). Se consideran como salidas del proceso el voltaje entregado por el sensor de nivel (VN) y el voltaje entregado por el sensor de caudal (VC). El nivel entregado por el sensor de nivel se referencia cono N y el caudal entregado por el sensor de caudal como C.
Para determinar si hay o no interacción entre los lazos se aplica el método de ganancias relativas (Bristol, 1996). Este consiste en calcular las ganancias en lazo abierto y las ganancias relativas; con base en estas se escoge la combinación de lazos adecuada (Smith y Corripio, 1997).
El cálculo de las ganancias en lazo abierto y relativas se realiza mediante una prueba experimental que consiste en aplicar un escalón constante durante todo el tiempo de la prueba a una variable de entrada, mientras que la otra variable es sometida a un cambio de escalón en el tiempo t0 y así observar cómo es el comportamiento de las variables de salida (Figura 4 y 5).
VNAPROX y VCAPROX corresponden a la regre- observa una variación en VC y una variación despresión lineal de VN y VC respectivamente. La Figura 4. muestra que ante el cambio en el escalón de VB se experimenta un aumento en la pendiente de VN, Obtenida esta información, se calculan las ganan pero no se evidencia ninguna variación en VC. En la Figura 5. ante el cambio en el escalón de VV se observa una variación en VC y una variación despreciable en la pendiente de VN.
Obtenida esta información, se calculan las ganancias en lazo abierto y las ganancias relativas para cada variable.

De lo anterior se obtiene la matriz de ganancias relativas, Tabla 1. donde se evidencia que el sistema puede ser tratado como dos subsistemas SISO desacoplados y se establece que el Nivel debe ser controlado por VB y el caudal por VV, dado al alto grado de interacción que se presenta entre las variables de entrada y salida mencionadas.
El modelamiento de los dos subsistemas de la planta se basa en pruebas experimentales del proceso haciendo uso del System Identification Toolbox (Osorio, 2015), con el cual se obtienen las funciones de transferencia del sistema.
Para la variable nivel, se considera como entrada el voltaje de la bomba y como salida el voltaje de nivel, dejando el voltaje de la válvula en cero y por consiguiente el caudal en cero. Se obtiene el modelo del subsistema con una aproximación de 93.78%, Figura 6. y la función de transferencia. Ecuación 9.
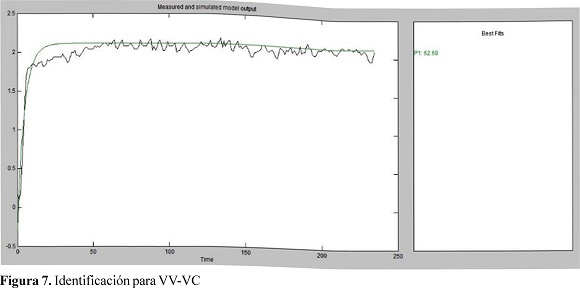
Para el caudal, se considera como entrada el voltaje de la válvula y como salida el voltaje de caudal, dejando el voltaje de la bomba en un valor estable para que se mantenga un nivel en el tanque. Se obtiene el modelo del subsistema con una aproximación de 62.68%, figura 7 y la función de transferencia, Ecuación 10.
Toma como variable manipulada el voltaje aplicado a la bomba VB y como variable controlada el voltaje de nivel VN. Se aplica un control por modelo interno, ya que las entradas de la red son la salida real de la planta y el error entre la salida del modelo directo y la salida real de la planta.
Con la ayuda del Neural Network toolbox de MatLab se desarrolla el algoritmo encargado de crear la red neuronal con los datos del error de voltaje nivel y el voltaje de nivel (VN), la cual posee una capa oculta con 13 neuronas y una capa de salida con 1 neurona. Para la elección del número de neuronas en las capas ocultas no existe una regla, se deben hacer pruebas y elegir el número con el que tenga mejor comportamiento (Rocha y Escorcia, 2010). La función de activación usada para la capa oculta fue sigmoidal tangencial hiperbólica, que al ser una función no lineal permite a la red aprender relaciones lineales y no lineales entre la entrada y la salida. La función de activación utilizada para la capa de salida es lineal, pues no modifica la salida calculada por la capa oculta y además puede tomar cualquier valor (Llano, et al., 2007). El método de entrenamiento seleccionado fue el de Levenberg-Marquardt, ya que está diseñado especialmente para disminuir el error cuadrático medio, un parámetro fundamental en en el diseño de controladores neuronales (Zarza y Tribaldos, 2012), (Goméz., et al, 2013).
Toma como variable manipulada el voltaje aplicado a la válvula de control VV y como variable controlada el voltaje de caudal VC. Con la ayuda del Neural Network toolbox de MatLab se desarrolla el algoritmo en el cual se crea la red neuronal del modelo inverso del sistema, formada por una capa oculta con 5 neuronas y la capa de salida con 1 neurona. Las funciones de activación usadas son las mismas de la red neuronal para el nivel, en la capa oculta la función sigmoidal tangencial hiperbólica y en la capa de salida la función lineal. El método usado para el entrenamiento es también el de Levenberg-Marquardt. La interfaz de control en tiempo real, implementada en Simulink, a través de la cual se realizan las pruebas de los controladores se muestra en la Figura 8.
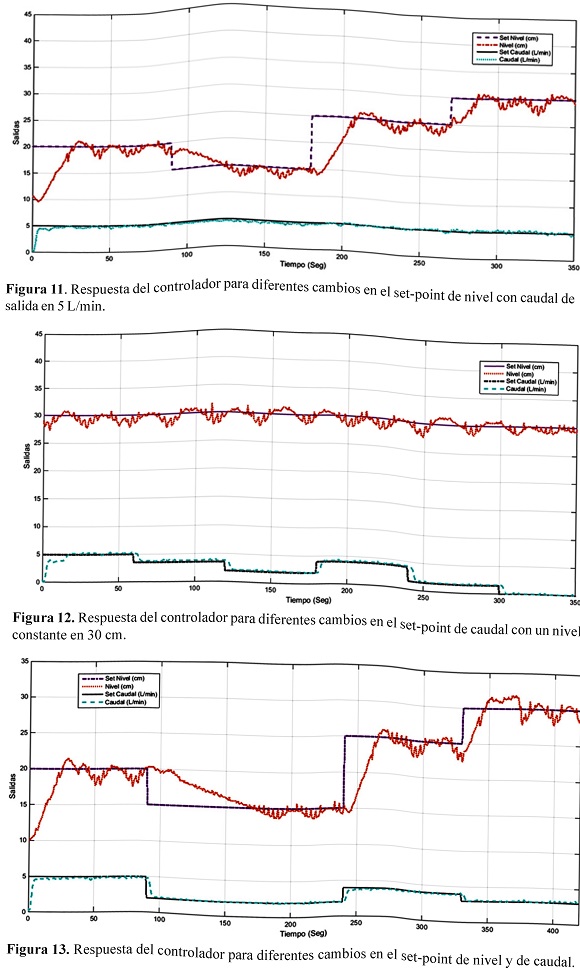
Se realizan pruebas del controlador en tiempo real obteniendo los siguientes resultados (Figuras 9 a la 13).
Al comparar los resultados de todas las pruebas rea-lizadas se observa en lasFiguras 9 a 13 que la variable caudal se establece aproximadamente a los 5 segundos, excepto cuando se presentan burbujas en la tubería, lo cual toma al fluido turbulento y sólo se establece al alcanzar un flujo laminar. El tiempo de establecimiento de la variable nivel depende del valor de setpoint que se desee alcanzar, además del caudal que esté saliendo en ese momento, pues esto representa una perturbación al control de nivel, lo que ocasiona fluctuaciones en el estado estable de dicha variable.
Para realizar la validación de los controladores en simulación y en tiempo real se aplica un set-point de nivel de 30 cm y un set-point de caudal de 5 L/min como se muestra en la Figura 14.
Donde se evidencia que la respuesta entre el caudal simulado y el caudal en tiempo real son muy aproximadas con una diferencia en el tiempo de establecimiento de 5 segundos, puesto que en tiempo real tarda 5 segundos en alcanzar su valor de estado estable y en simulación tarda 10 segundos en lograrlo. Para la variable nivel, la respuesta en tiempo real y simulada difieren en su comportamiento en estado transitorio, dado que la primera no presenta sobreimpulso y tiene un tiempo de establecimiento de 45 segundos, a diferencia de la respuesta simulada, la cual presenta un sobreimpulso de 39.15% y un tiempo de establecimiento de 130 segundos; esto se debe a que el modelo matemático más aproximado que genera el IDENT es el de un sistema subamortiguado de segundo orden y como tal, su respuesta ante un escalón va a ser la propia de este tipo de sistemas, por lo cual no describe de manera precisa las características dinámicas de la bomba. Pero se observa que el comportamiento en estado estacionario es muy aproximado.
La comparación del desempeño del control neuronal frente al control difuso se realiza evaluando tres parámetros: sobreimpulso, error en estado estacionario y tiempo de establecimiento. Los resultados para el controlador basado en redes neuronales obtenidos en este trabajo se pueden ver en la Tabla 2. Para el controlador difuso es necesario remitirse a la Tabla 3, Figura 14. disponible en (Ramírez y Calvache, 2013) donde se habían registrado estos valores obtenidos de la misma planta.
Se evidencia que el error en estado estacionario disminuye notablemente dado que el porcentaje de error máximo es de 0.01% y 0.003% por redes neuronales y de 3% y 1.75% por control difuso, para nivel y caudal respectivamente. En cuanto al sobreimpulso, aunque en el control difuso es mínimo, el control por redes neuronales lo elimina en las dos variables controladas. Para el tiempo de establecimiento se observa que el control neuronal también mejora considerablemente para las dos variables, esto se puede observar en la Tabla 3, donde RNA (Redes Neuronales).
De acuerdo a la matriz de ganancias obtenida al aplicar el método de ganancias relativas (Bristol, 1996), no existe interacción alguna entre los lazos VB-VN y VV-VC, por lo que el sistema hidráulico puede considerarse como dos sistemas SISO independientes. Por tanto, el uso de técnicas de desacople no son necesarias.
La técnica del modelo inverso permite desarrollar controladores neuronales con características particulares de acuerdo al tipo de aplicación requerida. Para el caso de la variable caudal, al presentar una dinámica de complejidad moderada, la técnica del modelo inverso simple es suficiente para establecer una relación directa entre la entrada y la salida, sin requerir una realimentación o un procesamiento del estado actual de la variable controlada. Cuando el comportamiento de la variable a controlar es más complejo y además está expuesto a perturbaciones, como en el caso del nivel, es preciso utilizar una variación del modelo inverso conocida como modelo interno, que permite examinar las condiciones actuales de la variable controlada, evaluar el error y tomar las acciones correctivas necesarias para alcanzar el punto de establecimiento deseado.
Las simulaciones del controlador son consistentes con el rendimiento que se presenta durante las pruebas en tiempo real. Si bien existen algunas diferencias en el régimen transitorio de la respuesta de la variable nivel, estas se atribuyen a que el modelo de segundo orden no representa en su totalidad las características dinámicas del actuador implicado, en este caso, la bomba. Esta aproximación produce un sobreimpulso característico de este tipo de sistemas, no obstante, el tiempo de establecimiento es muy similar en los dos casos.
El control basado en redes neuronales es superior al realizado mediante lógica difusa de acuerdo a los criterios evaluados, dado que se evidencia un mejoramiento del error en estado estacionario y del tiempo de establecimiento, a la vez que elimina por completo el sobreimpulso de las dos variables controladas del proceso.
Como desventaja del control implementado se menciona el costo computacional que se puede incrementar dado que la adquisición y control se hacen ambas mediante la interfaz de MatLab, aunque en las pruebas se muestra que el trabajo en tiempo real presenta un delay que no afecta sutancialmente la respuesta del sistema, queda planteada la opción de trabajar con herramientas de mejor desempeño en tiempo real como Lab VIEW o software libre.
Aliasghary, M., Naderi, A., Ghasemzadeh, H., Pourazar, A., 2011. Design of Radial Basis Function Neural Networks, Controller Based on Sliding Suface for a Coupled Tank System. Engineering Istanbul Technical University. Turkey.
Armijos, L., Chicaiza, D., 2011. Diseño e implementation de controladores inteligentes en el control de nivel de un sistema multi-tanque. Escuela Politécnica del Ejército. Sangolquí, Ecuador.
Bristol, E. H., 1996. On a New Measure of Interaction for Multivariable Process Control. IEEE Transaction on automatic control, pp. 133-134.
Castelo, G., Garrido, J., Vázquez, F., 2009. Ajuste, configuración y control de cuatro tanques acoplados. Universidad de Córdoba.
Dreyfus, G., 2005. Neural Networks: Methodology and Applications. Springer (Ed), p. 498.
Garrido, J., Reina, R, Vázquez, M., García, A., 2009. Control de Nivel a través de Redes Neuronales. Universidad Tecnológica del Sureste de Veracruz.
Goméz, L., Sossa, EL, Barrón, R., Cuevas, F., Jimenez, J., 2013. Redes Neuronales Dinámicas a la Recomendación musical optimizada, pp. 47-10.
Llano, L., Hoyos, A., Arias, F., Velásquez, J., 2007. Comparación del Desempeño de Funciones de Activación en Redes Feedforward para aproximar Funciones de Datos con y sin Ruido. Universidad Nacional de Colombia, sede Pereira. Vol. 4, Núm. 2.
Majstotovic, M., Nikolic, I., Radovic, J., Kvascev, G., 2008. Neural network control approach for a two-tank system. 9th Symposium on Neural Network Applications in Electrical Engineering, NEUREL-2008. Belgrade, Serbia.
Moromenacho, E., Rosero, C., Bravo, Y., 2010. Control Predictivo en tanques acoplados. Escuela Politécnica Nacional. Quito, Ecuador.
Osorio, C., 2015. Extracción de Modelos Dinámicos Directamente de Datos Experimentales usando Identificación de Sistemas. Mathworks. Disponible en web http://www.mathworks.com/videos/extracting-dynamic-models-from-experimental-data-using-system-identification-spanish-100499.html
Parker, D. B., 1995. Optimal algorithms for adaptive networks: Second order backpropagation, second order direct propagation and second order Hebbian learning. En: D.B. Parker IEEE 1st Int. Conf. on Neural Networks, San Diego, CA. vol.2, pp. 593- 600.
Ponce, Cruz, P., 2010. Inteligencia Artificial con Aplicaciones a la Ingeniería. Alfaomega (Ed). 376 págs.
Ramírez, G, Calvache, O., 2013. Diseño e Implementation de un Controlador Multivariable de Nivel y Flujo Utilizando Microcontroladores Especiales para Lógica Difusa. Neiva, Colombia.
Ramli, M., Ahmad, R., Ismail, R., 2009. Comparison of Swarm Adaptive Neural Network Control of a Coupled Tank Liquid Level System. International Conference on Computer Technology and Development. Malaysia.
Recalde, L., Burbano, R., 2006. Control Adaptativo Multivariable en línea. Escuela Nacional Politécnica. Quito, Ecuador.
Rocha, C., Escorcia, J., 2010. Sistema de Visión Artificial para la Detección y el Reconocimiento de Señales de Tráfico Basado en Redes Neuronales. 8th LACCEI Latin American and Caribbean Conference for Engineering and Technology (LACCER’2010).
Smith, C. y Corripio, A., 1997. Principles and Practice of Automatic Process Control, John Wiley & Sons, New York.
Torres, L., Anzurez, J., 2013. Adaptive Neuro-Fuzzy Inference System Control for a Two Tanks Hydraulic System Model. Power, Electronics and Computing (ROPEC), 2013 IEEE International Autumn Meeting on Automatic Contrand Systems Engineering. University of Sheffield. United Kingdom.
Vassiljeva, K., Belikov, J., Petlenkov, E., 2014. Application of genetic algorithms to neural networks based control of a liquid level tank system. International Joint Conference on Neural Networks (IJCNN). Beijing, China.
Zarza, E., 2012. Desarrollo de Redes Neuronales Artificiales para el Cálculo del Transporte Neoclásico en Reactores de Fusión. Madrid-España.