
Myriam R Pallares Muñoz1, Julián A Pulecio Diaz2
Se evalúa la influencia de la presión de conlaclo de una carga dual sobre los parámetros de diseño de pavimentos asfálticos por medio del modelador de elementos finitos EverStressFE 1.0 intentando reproducir de una manera más ajustada la forma de la huella y la intensidad de esfuerzo generados por las llantas de los vehículos. Para la validación se cmplcócl software muí licapa clást ico EverStressⒸ5.0. Los resultados de las deformaciones llevaron a concluir que los diseños de pav intentos asfálticos rcali/ados con métodos analíticos pueden estar ligeramente sobrcdimcnsionados y en consecuencia elevar los costos de construcción de los pavimentos Este estudio traza una ruta para analizar la sensibilidad de distintos factores que pueden afectar el diseño de pav intentos asfálticos. Se espera en próximas investigaciones integrar condiciones dinámicas introduciendo resultados obtenidos de pruebas de campo a escala real
Palabras clave: EverStressFE©1.0; EverStress©5.0; modelado tridimensional de pav intentos; área de contacto; huella de llama; distribución de presión de inflado; modelado de pav intentos con software libre
The influence of a dual tire pressure on lite design parameters of asphalt pavements using finite clement modeling EverStressFE©1.0 is evaluated This is try ing to represent more adjusted the footprint shape and intensity of stress generated by the tires of vehicles To validate the clastic multilayer EverStressⒸ5.0 software was used. The results of the deformations can be concluded that the asphalt pavement designs made w ith analy tical methods may be slightly oversized and consequently increase the cost of constmction of pavements This study marks a route to analyze tltc sensitiv ity of v arious factors that may affect the design of asphalt pavements. Future research is expected to integrate dy namic conditions by introducing results of field tests to full scale.
Key words: EverStressFEⒸ1.0; EverStressⒸ5.0; three-dimensional modeling of pavements; contact area; tire tread; tire-footprint-pressure-distribution; free-software pavement modeling
En la actualidad en el diseño de estructuras de pavimento se emplean métodos analíticos y/o modelos numéricos. definiendo para ello: el eje de diseño (eje simple de 13T de cuatro ruedas, 2 en cada extremo), el espesor de las capas y las características de los materiales De manera que se pueda calcular las deformaciones a tensión en las fibras inferiores de las capas asfálticas y a compresión en la subrasante, provocadas por la presión de contacto de la carga de diseño que tradicionalmente se aplica de manera homogénea en un área circular sobre la superficie de rodadura como se ilustra en la figura 1. Esta variable ha sido objeto de estudio de investigaciones que afirman que "la presión de contacto no se distribuye uniformemente, lo que proporciona alguna información para justificar por qué el supuesto de área de contacto convencional está incorrecto" (Xia, 2010) Esta premisa ha sentado las bases de un estudio para evaluar la influencia de la presión de contacto de una carga dual sobre los parámetros de diseño de pavimentos asfálticos (deformaciones horizontales“εxx” y verticales "εzz") Para este propósito se empleó el modelador tridimensional de elementos finitos EverStressFE I Oque permite reproducir de una manera más ajustada la forma de la huella y la intensidad de esfuerzo generados por las llantas de los vehículos de diseño (figuras 2 y 3) y el software multicapa elástico EverStressO 5.0 para validar los resultados.

El análisis se abordó por medio de los modeladores computacionales EverStressO 5 0 y EverStressFE 1.0. el pnmero se utilizó para validar los resultados de los modelos de elementos finitos dada su versatilidad y funcionalidad Is estructura de pavimento asfáltico representada es se mi-flexible compuesta por una base de grava (GB) y una capa de rodadura de concreto asfáltico (BBSG) como se muestra en la figura 4.
Las dimensiones de las capas constitutivas de la estructura de pavimento modelado se presentan en la Tabla 1. La condición de frontera considerada para la subrasante es semi-infinita y como es común en el dimensionamiento de este tipo de estructuras se trabajaron las interfaces ligadas.
Los módulos de elasticidad tomados como referencia para cada una de las capas de acuerdo a las condiciones de trabajo del pavimento se muestran en la Tabla 2. El módulo de elasticidad de la subrasante conocido como resiliente se determina por medio de ensayos triaxiales; el módulo elástico de las capas asfálticas se establece a través de ensayos de módulos resilientes ó dinámicos a temperaturas y frecuencias de diseño (LCPC, 1994), (AASHTO, 2008), (Knngos etal, 2013) o a través de tramos experimentales sobre los que se realizan ensayos deflectómetricos Falling Weight Deflectometer (FWD) ó Heavy Weight Deflectometer (HWD) acompañados de análisis inversos o de retro-calculo y corregidos alas condiciones de laboratorio (Papagiannakis, 2008), (Rabaiottia et al. 2013).
Ya que la variación del módulo de Poisson no tiene incidencia considerable en el comportamiento del pavimento (Rodríguez, 2005a), (Rodríguez, 2014b), se emplearon los valores característicos de la Tabla 3. Los espesores típicos, los módulos elásticos y las relaciones de Poisson fueron tomados de la Guía Francesa para el Diseño de Pavimentos Asfálticos por MetodologíaRacional “Conception et dimensionnement des structures de chaussée, Guide technique” del antiguo Laboratoire Central des Ponts et Chaussées (LCPC) (LCPC, 1994), hoy por hoy, Instituí Franjáis des Sciences et Technologies des Transports, de L’aménagement et des Réseaux (IFSTTARs), entidad de investigación reconocida a nivel mundial y líder en Europa.
La determinación de los parámetros de diseño de pavimentos tienen principio en el diseño racional que consiste en modelar la estructura a partir de la definición de los espesores y las rigideces (módulos resilientes, dinámicos y de Poisson) de cada capa para calcular las tensiones y compresiones provocadas por una carga tipo e identificar: a) la deformación a tensión máxima (εt) capaz de producir la rotura de las capas asfálticas; esta deformación se compara con el límite admisible del material asfáltico (εtadm) que es función de múltiples factores, entre ellos, el tránsito, coeficientes de calibración y riesgo, efecto de las heterogeneidades locales de rigidez de las capas ligadas y deformación a un millón de solicitaciones con una probabilidad de falla del 50% determinado a 10°C y 25Hz (LCPC, 1994); b) la deformación a compresión máxima (εc) sobre la subrasante que se compara con la admisible (εcadm) y que depende del nivel de tránsito (LCPC, 1994).
Se desarrolló el modelo en el programa elástico multicapa de cálculo de esfuerzos y deformaciones para diseño de pavimentos EverStress© 5.0, introduciendo una presión de inflado distribuida uniformemente sobre un área circular de radio 0.125m bajo una presión de 0.662 MPay distancia entre ejes de 0.375 m. El análisis permite identificar las deformaciones características de control del diseño estructural del pavimento, tales como las deformaciones a tensión en las fibras inferiores de las capas asfálticas y compresión en la parte superior de la subrasante (LCPC, 1994). En la figura 5 se indica la ubicación de estos parámetros.
Los modelos de elementos finitos con el modelador tridimensional elástico EverStressFE 1.0 fueron validados con el programa EverStressC 5.0 La figura 6 muestra el elemento finito que emplea el software; se trata de un elemento tipo BRICK con tres grados de libertad por nodo(UX, UY, UZ) El EverStressFE 1.0 trabaja con mallados de distintos grados de refinamiento y se compone de cinco interfaces que realizan diferentes funciones a) Geometry and layer properties, contiene una herramienta CAL) que permite construir un modelo geométrico e introducir los datos característicos de las capas (espesores y módulos) y definir las fronteras del dominio del modelo, b) Loads, almacena los parámetros de carga, tipo de rueda y eje. contacto, presión, carga, ancho y espaciamiento de las llantas, distancia entre ejes y formas de distnbución de la presión de contacto de la rueda, c) Meshing, determina los parámetros de mallado (tipo de malla y refinamiento. división de elementos, condición de interfaz y ngidez)y especificaciones del modelo (número de nodos y elementos finitos), d) Solver, ejecuta el solucionador de elementos finitos, e) Results, permite obtener los resultados del análisis Los pasos típicos del procedimiento de análisis de un problema de esfuerzo-deformación con EverStressFE 1.0. son ingresar los datos de dimensionamiento. numero de capas, espesores y parámetros de ngidez (módulos resilientes, dinámicos y de Poisson), condiciones de frontera, valores de presión, carga, ancho y espaciamiento de las llantas (el programa por defecto aplica un cuarto de carga dual según se observa en las figuras 7. 8 y 9). elegir una combinación de mallado. ejecutar el soluciorlador y obtener resultados (Davids, 2009a,b.c).
Validado el modelo de elementos finitos con el área de contacto circular, se procedió a desarrollar tres modelos adicionales variando únicamente la distnbución de la presión de contacto de la carga dual de manera más ajustada a la realidad (figuras 2 y 3). Los análisis se desarrollaron con los mismos parámetros de rigidez, espesores, distancia entre ejes y presión de contacto, teniendo en cuenta un área de huella rectangular cuyo ancho de banda "TíreTread Width" se calcula a partir de las expresiones (1) y (2) La figura 10 justifica la procedencia del nuevo dato de cálculo.
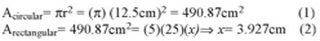
Donde x es el ancho de banda de llanta, A es el área de la huella y r es el radio del área circular.
Definida la forma de la huella, se evaluaron diferentes distribuciones de la presión de contacto constante, parabólica y media onda sinusoidal como se muestra en las figuras 11.12 y 13; destacando que el pulso sinusoidal es característico en la determinación de la curva maestra de ensayos dinámicos de concreto asfáltico, de hecho, la prueba de módulo dinámico mide la relación esfuerzo-deformación de una muestra bajo un pulso de carga sinusoidal continuo (Brown el al, 2001),(Witczak el al, 2002), (Bonaquist, 2005) Al igual que en el caso de área de contacto circular, el programa ubica la carga dual a un cuarto( 1/4-simétrica) para optimizar el tiempo de cálculo (Davids, 2009a, b, c) Las ilustraciones del caso se presentan en las figuras 14, 15 y 16.
En la Tabla 4 se presentan los resultados del modelo analítico realizado con EverStressO 5.0 - uiilizathcomo validatlor y del modelo de elementos finitos Ever StressFE 1.0 trabajado con área de contacto circular.
Se observa que los porcentajes de variación del modelo numérico frente al analítico son inferiores al I % lo cual permite concluir que las decisiones tomadas en la modelación con EverStressFE 1.0 son adecuadas para implementar los modelos que introducen modificaciones en la forma de la huella y la presión de contacto de la llanta. En las figuras 17 y 10 se presentan los resultados del modelo analítico; los valores subrayados corresponden a los parámetros del diseño racional.
De los resultados contenidos en las figuras 17 y 18 se verifica que: 1) la deformación máxima a compresión sobre la subrasante en el modelo multicapa elástico está bajo la llanta y no en el centro de la carga dual, 2) las deformaciones máximas en las fibras inferiores de las capas asfálticas BBSG y GB están bajo el centro de la carga dual y no bajo la llanta.
Las figuras 19,20y 21 muestran los resultados gráficos de deformación, correspondientes a los parámetros del diseño racional por medio de isocontomos La figura 19 representa las deformaciones exx situadas en la fibra inferior de la capa asfáltica BBSG se observa la concentración de esfuerzos en la zona de aplicación de la carga El semicírculo corresponde a un cuarto de carga dual con la forma típica de la huella empleada por el método racional Los valores de deformación εxx mostrados en la figura 19, sugieren un comportamiento a compresión de la capa asfáltica inclusive en la fibra inferior lo cual probablemente es atribuible al módulo de la capa asfáltica de rodadura BBSG a la rigidez de la capa contigua GB y a la misma condición de liga de las interfaces El valor de deformación máxima εxx en esta capa se sitúa en el centro de la carga dual (coordenadas X O.Y 2900) tal como lo sugiere el modelo multicapa.
La figura 20 representa las deformaciones exx situadas en la fibra inferior de la capa asfáltica GB los valores de deformación mostrados en la figura, denotan el tipico comportamiento a tensión de la capa asfáltica como lo sugiere el método racional en el control de diseño El valor de deformación máxima εxx en esla capa se sitúa en el centro de la carga dual (coordenadas X=0, Y=2900) tal como lo indica el modelo multicapa.
Los isocontomos de deformación vertical de la figura 21 siguen el patrón de la huella circular, encontrándose que el valor de deformación máxima vertical εzz en esta capa se sitúa en el centro de la carga dual (coordenadas X 0, Y 2900) y no en el centro de la llanta como lo sugiere el modelo multicapa, lo cual probablemente es debido a la carga dual y/o a la misma rigidez de la estructura y de la subrasante.
Se desarrollaron tres modelos para analizar la respuesta a la deformación de la estructura de pavimento cuando se emplea un área de contacto y una distribución de la presión de inflado de las llantas sobre la superficie de manera más ajustada a la realidad HI área de contacto corresponde a la huella típica rectangular mostrada en la figura 3 y se evaluaron las distribuciones de presión constante, parabólica y media onda sinusoidal délas figuras 11, 12 y 13 respectivamente.
La figura 22 presenta el desarrollo de la deformación exx en la fibra inferior de la capa asfáltica BBSG con presión de inflado constante En el centro de la carga dual ubicado en las coordenadas X=0. Y=2900yZ=60 cm se encuentra la máxima deformación normal εxx=-39.77F.-06 (-39.77 microstrain) Fstadeformación por ser de compresión se considera no representativa en el diseño y señala que el eje neutro de la estructura se encuentra por debajo de la capa de rodadura BBSG En adelante el análisis de resultados se desarrollará respecto al modelo de referencia de presión constante y área de contacto circular Al comparar los resultados de isocontomos de deformación εxx con los del modelo de referencia, se observa que el rango de valores de deformación es similar, al igual que la distribución de los isocontomos en el plano. Las deformaciones promedio de mayor valor se encuentran capturadas dentro de la huella rectangular. La distribución de la deformación indica que la huella rectangular es una buena representación del contacto de la llanta con la superficie del pavimento
La figura 23 presenta los resultados de la deformación åxx en la fibra infenor de la capa asfáltica GB Entendiendo al pavimento como un elemento sometído a flexión, se aprecia que el eje neutro de la estructura se encuentra dentro del dominio de esta capa La máxima deformación normal εxx es 80 92E-06 (80.92 microstrain). está ubicada en el centro de la carga dual con coordenadas X=0. Y=2900. pero con Z=240 cm y representa d estado de tensión característico dd diseño racional.
La figura 24 representa la deformación εzz sobre la subrasante La máxima deformación normal εzz de -253.27E-06 (-253.27 Microstrain) está ubicada en las coordenadas X=0, Y=2900 y Z=240 cm
La Tabla 5 contiene el resumen de los resultados comparados con los obtenidos del modelo elástico multicapa EverStress 5.0, determinando porcentajes de variación bajos y poco significativos.
La figura 25 indica la deformación εxx en la fibra inferior de la capa asfáltica BBSG Al comparar los resultados de isocontomos de deformación εxx con los del modelo de referencia, se observa que el rango de valores de deformación es similar, no obstante, la dis-tnbución de los isocontomos en el plano es ligeramente diferente, esto es, el contorno de deformación máxima se concentra en el centro de la carga dual, significando menor densidad de deformación normal a compresión alrededor de la huella.
En la figura 26 se presenta la deformación cxx en la fibra inferior de la capa asfáltica GB. La máxima deformación normal εxx es 78 95E-06 (78.95 microstrain) y se ubica en las coordenadas X 0, Y 2900 y Z=240 cm.
La figura 27 reproduce la deformación ezz sobre la subrasante En la coordenada X 0,Y 2900 y Z 240 cm se ubica la máxima deformación normal a compresión εzz de -251 67E-06 (-251.67 microstrain) Al comparar los resultados de isocontomos de deformación εzz de la figura 27 con los del modelo de referencia, se observa que el isocontomo de deformación máxima es más amplio denotando un mayor rango de afectación a compresión Adicionalmente, dentro de la huella se desarrollan más isocontomos denotando menos homogeneidad o uniformidad de deformación dentro de la misma.
La tabla 6 contiene el resumen de los resultados comparados con los obtenidos del modelo elástico multicapa EverStress 5.0 Este resultado llama la atención porque las deformaciones εxx y εzz, son variables representativas del diseño y los porcentajes de variación sugieren posibles sobredimen-sionamientos, por consiguiente mayores costos de la estructura.
multicapa EverStress 5.0 Este resultado llama la atención porque las deformaciones εxx y εzz, son variables representativas del diseño y los porcentajes de variación sugieren posibles sobredimen-sionamientos, por consiguiente mayores costos de la estructura.
La figura 28 nos muestra el mapa de colores de la deformación cxx en la fibra inferior de la capa asfáltica BBSG La máxima deformación normal εxx es -39 30E-06 (-39 30 mierostrain) y se encuentra en las coordenadas X=0, Y=2900 y Z=60 cm.
La figura 29 expone el mapa de colores de la deformación cxx en la fibra inferior de la capa asfáltica En las coordenadas X=0, Y=2900 y Z=240 cm se presenta la máxima deformación normal εxx de 78 61E-06 (78 61 mierostrain).
En la figura 30 se presenta el comportamiento de la deformación εzz sobre la subrasante La máxima deformación normal εzz es -25I.I8E-06 (-251.18 microstrain) y se ubica en las coordenadas X= 0. Y=2900y Z=240cm
La tabla 7 presenta el resumen de los resultados comparados con los valores obtenidos del modelo elástico multicapa EverStress 5.0, encontrándose porcentajes de variación de I 26% y 6 71% para las capas asfálticas y 5.19% sobre la subrasante Este escenario también llama la atención, porque las deformaciones εxx y εzz determinadas por el método analítico se encuentran 6 30 y 5.01% por encima de los resultados del modelo de elementos finitos, suginendo sobredimensionamiento de la estructura Probablemente, d diseño racional debería ajustarsea condiciones más reales de area de contacto y distnbución de presión.
En todos los casos modelados con elementos finitos, la deformación εzz máxima en la subrasante es mayor bajo el centro de la carga dual y no bajo una llanta como lo sugiere el modelo multicapa elástico, probablemente por la carga dual y/o la misma rigidez de la estructura y de la subrasante Las causas serán estudiadas en futuros análisis.
Si se observa con cuidado los porcentajes de variación reportados en las tablas, es posible concluir que los diseños realizados con métodos analíticos están siendo ligeramente sobredi-mensionados. Por ejemplo, las deformaciones åxx obtenidas del análisis con presión constante circular y presión media onda sinusoidal en la capa GB son: 84 26E-06 y 78 6IE-06 respectivamente. que en términos de número de ejes simples equivalentes con carga dual de 13T corresponde a 3620783 y 5122958 NE con espesores de 0.180m y 0.195m, revelando una diferencia de espesor de 0.015 m que constructivamente se traduce en 2 cm adicionales de espesor en el diseño y en consecuencia mayores costos de obra.
El método de los elementos finitos ha demostrado ser muy eficaz y en el caso particular, permitió evaluar la influencia de la presión de contacto de una carga dual sobre los parámetros de diseño de un pavimento, por lo tanto marca un camino a seguir para estudiar la sensibilidad de distintos factores que pueden afectar el diseño de pavimentos asfálticos.
Generado el interés de profundizar en la influencia de la presión de contacto de una carga dual sobre los parámetros de diseño de pavimentos asfálticos, en próximos estudios se analizarán condiciones dinámicas introduciendo resultados obtenidos de pruebas de campo a escala real.
AASHTO. 2008. Mechanistic-Empirical Pavement Design Guide. A Manual of Practice American Association of State Highway .and Transportation Officials. USA
Bonaquist. R and Christensen. D.W., 2005 Practical procedure for developing dynamic modulus master curves for pavement structural design Transportation Research Record, pp 208-217
Brown, E R . Kandhal, P S.. Zhang, J., 2001. Performance Testing for Hot Mix Asphalt. NCAT Report No. 01-05. University of Auburn, National Center for Asphalt Technology. Auburn Alabama USA.
Davids, W. G. 2009. EverStressFEI .O Software for 3D Finite-Element Analysis of Flexible Pavement Structures. The Washington State Department of Transportation Washington USA.
Davids, W. G. 2009 EverStressFEl 0Theory Manual The Washington State Department of Transportation. Washington USA
Davids, W G. 2009. EverStressFE 1.0 Software for 3D Finite-Element Analysis of Flexible Pavement Structures: Summary of Features and Capabilities. University of Maine. AEWC Advanced Structures and Composites Center Maine USA
Knngos. N , Birgisson, B , Frost, D, Wang, L, 2013. Multi-Scale Modeling and Characterization of Infrastructure Materials, Proceedings of the International RII.F.M Symposium: Estocolmo, Springer
LCPC, 1994 Conception et dimensionnement des structures de chaussée. Guide technique LCPC and SETRA. Pans
Papagiannakis. A. T. Masad, E. A. 2008 Pavement Desiijn and Materials John Wiley & Sons Texas USA
Rabaiottia, C . Puzrinb. A . Caprezb. M . Ozanc. C . 2013 Pavement structural health evaluation based on inverse analysis of three dimensional deflection bowl International Journal of Pavement Engineering. 14(4), pp 374-387
Rodriguez. W.. Pallares M . 2014 Modelado tridimensional de un pavimento bajo carga dual con elementos finitos. DYNA 82 (189). pp. 30-38.
Rodriguez. W y Pallares M . 2005 Desarrollo de un modelo de elementos finitos para el diseño racional de pavimentos Tecnura, Tecnología y Cultura Afirmando el Conocimiento, pp 25-37
Witczak, M.W., Kaloush, K., Pellinen,T., El-Basyouny, M ., Von Quintus, H, 2002. NCHRP Report 465, Simple Performance Test for Superpave Mix Design Transportation Research Board, National Research Council Washington USA.
Xia, K , 2010 Finite element modeling of dynamic tire11 pavement interaction Pavements and Materials Testing and Modeling in Multiple Length Scales, pp 204-214.