Dayam Soret Calderón Rivera1, Claudia Fernanda Navarrete López2 y José Luis Diaz Arevalo3
En este trabajo se presenta un estudio acerca de la selección de la mejor distribución probabilística para la variable media multianual de la temperatura en el departamento de Boyad (Colombia), como base para futuras estimaciones y proyecciones de la variable en condiciones de incertidumbre. Se seleccionaron Lis distribuciones Normal. Gamma. Wcibult y LogNonual para ajustar los dalos, y para encontrar cual distnbu-ción ajusta mejor los datos se utilizaron lósentenos de información basados en la máxima verosimilitud de Akaike (Akaike Information Criterion) y Bayesiano (Bayesian Information Criterion). Se muestran los resultados tanto en forma tabular como gráfica, asi como un plano de las funciones de distribución probabilísticas más representativas en el área de estudio. Como resultado se obtiene que en general la dislnbución que mejor se ajusta es la Weibull.
Palabras clave: Distribuciones de probabilidad;Temperatura;Criterios de información; Boyacá.
This paper presents a study on the selection of the best probabilistic distribution for multi-year average temperature variable in the department of Boyacá (Colombia) as the basis for future estimates and projections of the variable under uncertainty arises. Normal. Gamma. Weibull and lognormal distributions were selected to fit the data. To find which best fits the data criteria information based in maximum likelihood. Akaike (Akaike Information Criterion) and Bayesian (Bayesian Information Criterion) were used. The results are shown in both tabular and graphical form. as well as a map of the probabilistic distribution functions most representative in the study area. As a result we obtain that the Weibull distribution is the best fits in general.
Key words: Probabilistic Distributions; Temperature; Information criterion; Boyacá.
El objeto de éste trabajo es determinar la distribución probabilística de mejor ajuste para los datos medios multianuales de la vanable climatológica temperatura, en el departamento de Boyacá (Colombia). Estos datos fueron tomados del catálogo de estaciones climatológicas proporcionado por el IDEAM. Se probaron las distribuciones Normal. Gamma. Weibull y LogNormal para ajustar los datos (Navarrete. 2008. Minka 2002; Aristizabal, 2012. Martínez. 2011); y para encontrar cual distribución ajusta mejor los datos se utilizaron los criterios de información de Akaike(AIC) (Akaike. 1974) y Bayesiano (BIC) (Akaike. 1978. Schwarz 1978), Un aspecto importante de los criterios de información es que estos están asociados con el método de máxima verosimilitud, el cual, en modelos causales, está basado en el supuesto de que las variables observadas siguen una distribución normal multi variante (Caballero. 2011) La idea clave del AIC es la de penalizar un exceso de parámetros ajustados, mientras que en el BIC se penaliza el número de parámetros teniendo en cuenta que el AIC podria no ser asintóticamente justificable (Caballero. 2011; Montesinos. 2011; Ramirez. 2000).
Se encontró escasa información aplicada a series de datos hidrológicos (Ayodele. 2015. Chaouche. el. al.. 2010; Donat. 2012. Raisanen. 2009; Hingray. 2007), entre los cuales a nivel local se destaca el trabajo presentado por Dorado et. al. en el 2006 donde analizaron la v ariabilidad espacio-temporal de la precipitación mensual y anual en el área de influencia aguas abajo del embalse de regulación y abastecimiento SARA-BRUT, ubicado en el departamento del V alle del Cauca. Colombia Para el ajuste de las senes históncas se usaron modelos de distnbución de probabilidad teón-ca, como Gumbel. Normal. LogNormal y VV'akeby. y modelos de distribución empírica, como Weibull y Landwehr. Se utilizó la prueba de Error Estándar de Ajuste (EEA) para seleccionar el modelo teórico de mejor ajuste. El modelo Wakeby presentó el mejor ajuste en el 89%del total de estaciones analizadas, el cual corresponde a un modelo probabilistic» adecuado para representar los caudales de crecidas máximas dianas o instantáneas en una región No obstante para nuestro estudio, la distnbución Weibull se presenta como la
más confiable debido asu versatilidad (Behary Grimas, 2004). (Moreno el al.. 2011). En su trabajo de maestría (Navarrete. 2008) encuentra que para los criterios de AIC y BIC la distribución Weibull es la que mejor describe los datos
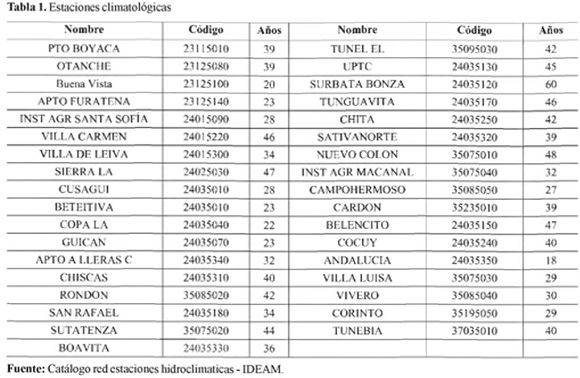
Este trabajo fue realizado sobre la totalidad de la extensión del departamento de Bovacá a partir de la in-fomiación proporcionada por el Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia (I DEAM). el cual cuenta con 35 estaciones meteorológicas en la región, las cuales se presentan en la tabla 1 junto con la extensión de la serie analizada De estas estaciones se obtuvo el promedio multianual de la vanable temperatura, y se realizaron los histogramas de frecuencia para cada una de las estaciones con la finalidad de determinar gráficamente las funciones a ajustar. No se consideró necesario realizar completado de datos ya que la vanable temperatura media presenta poca vananza (0.52 en promedio) y el porcentaje de datos faltantes global es bajo (3 60%).
Se aplicaron las pruebas de Mann-Kendall (Mann. 1945; Kendall. 1975) y Rachas con la finalidad de validar supuestos de homogeneidad y aleatonedad de las estaciones muestreadas Los resultados obtenidos mostraron que la mitad de las estaciones presentan un comportamiento homogéneo y aleatono Como el objetivo del trabajo es presentar las funciones de distn-bución de mejor ajuste a las senes de datos, no se realizaron transformaciones a las mismas.
Por medio de los software R * y ParameterSolver5 se procesaron los datos y se estimaron los parámetros, con el fin de hallar las distnbuciones de probabilidad y las funciones de máxima verosimilitud, las cuales fueron utilizadas para calcular los criterios de información Akaike (AIC) y Bayesiano (BIC). con base en estos se escogió la distnbución de mejor ajuste El AIC fue propuesto por Akaike, H. (1974) como un estimador insesgado asm tonco de la mfonnación de Kullback-Leibler esperada entre un modelo candidato ajustado yel verdadero modelo El BIC fue den vado por Akaike (1978) y Schwarz (1978) como una aproximación a una transformación de la probabilidad postenor de un modelo candidato.
Las distribuciones de probabilidad y los criterios se describen a continuación:
Distribuciones de probabilidad
Distribución normal: esta distribución de probabilidad continua es la más importante y la más utilizada, también llamada curva de Gauss. Esta dada por dos parámetros de la función f (ì,ó), donde ó representa la desviación estándar y µ la media de la muestra.
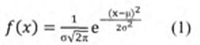
Distribución Gamma: es un caso especial de la distribución Pearson tipo III donde sus parámetros deben ser diferentes de 0. Esta distribución está dada por: Ã(á) la función gamma de á, â como el parámetro de escala y á es el parámetro de forma.
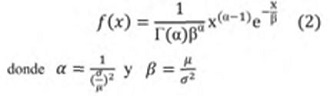
Distribución Weibull:esta distribución es muy versátil y es utilizada para modelar amplia gama de aplicaciones, describiéndose según los parámetros de escala y localización â. forma m y á como origen de la distribución.
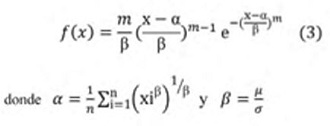
Distribución Log normal: al igual que la distribución normal está dada por los dos parámetros donde ó representa la desviación estándar y µ la media de la muestra
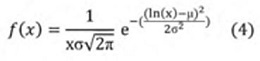
Máxima verosimilitud
La función de máxima de verosimilitud está dada por la máxima probabilidad de que ocurra o se dé una determinada muestra si es cierta la estimación que hemos efectuado, o el estimador que hemos planteado La densidad conjunta para esas observaciones es denotada como L = f(xi, p), y la máxima verosimilitud puede ser obtenida tomando la derivada de L. en relación con la probabilidad p) igualando la función a 0, para lo cual es mejor tomar logaritmos de la función L. y derivarlo; n es el número de observaciones.
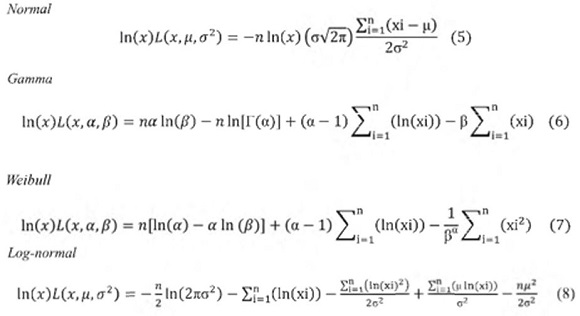
Calculo AlCy BIC
El criterio de información Akaike propuesto en 1974 y utilizado como un estimador insesgado, precisa que el modelo de probabilidad de menor valor A 1C es d que se selecciona como el mejor al que se le ajustan los datos La función está dada por la maximización del logaritmo de la máxima verosimilitud denotado como (In L) y K es el número de parámetros de la función de probabilidad (parámetros en el modelo):
AIC=2K-2ln(L)
La estructura del AIC está compuesta por la maximización del logaritmo de verosimilitud, es decir, como componente de la falta de ajuste del modeloy K como el número de parámetros estimados dentro del modelo como componente de penalidad I jx penalidad es una medida de la complejidad o compensación por el sesgo debido a la falta de ajuste cuando los estimadores de máxima verosimilitud son empleados (Bozdogan, 1987 en Acuña et. al. , 2012).
BIC sirve para la selección del modelo entre un conjunto finito de modelos, está estrechamente relacionado con el criterio AIC y se basa en parte en la función de probabilidad Para mejorarla inconsistencia del criterio AIC, Akaike 1978 y Schwarz 1978 presentaron un cnteno de selección de modelos desde la perspectiva bayesiana Schwarz estableció que la solución de bay es consiste en seleccionar el modelo con una alta probabilidad a posteriori El criterio de información bayesiana (BIC) se define como
BIC= 21n(L)+Kln (n)
Mapa de resultados
Una vez obtenidos los criterios AIC y BIC para cada una de las distribuciones por estación se procedió a realizar el mapa de área de influencia como se muestra en la figura 2
Después de obtener las distribuciones de probabilidad para cada una de las estaciones y de la aplicación de ios criterios AIC y BIC se observó que la distribución dominante en el departamento de Boyacá es la Weibull ajustándose a 21 estaciones de las 35 muestreadas (60%). en segundo lugar se encontraron las distribuciones Normal y Gamma con 6 estaciones cada una (17%) y por último la distribución Lognormal con 2 estaciones (6%) (tabla 2).
A continuación se presentan las figuras de las distribuciones de probabilidad para cada una de las estaciones cli matológicas del estudio, en color verde se puede apreciar la distnbución Weibull.
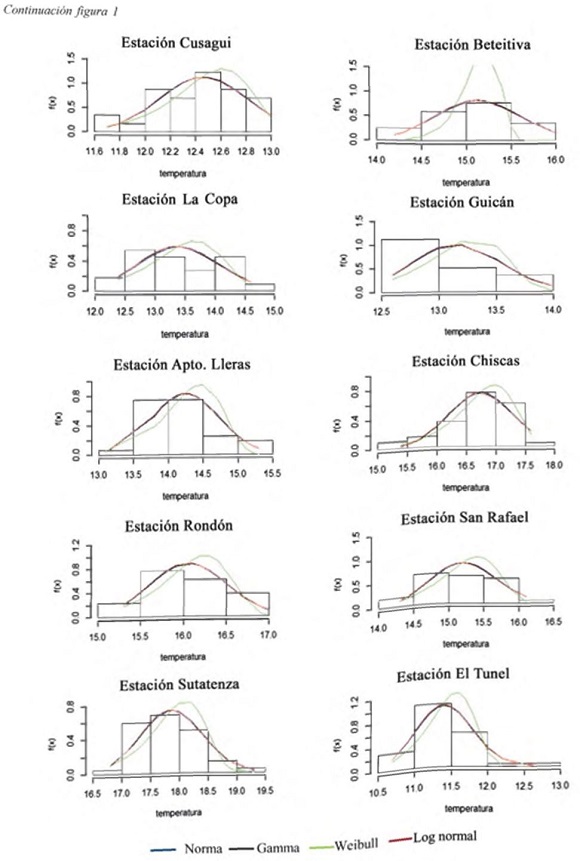
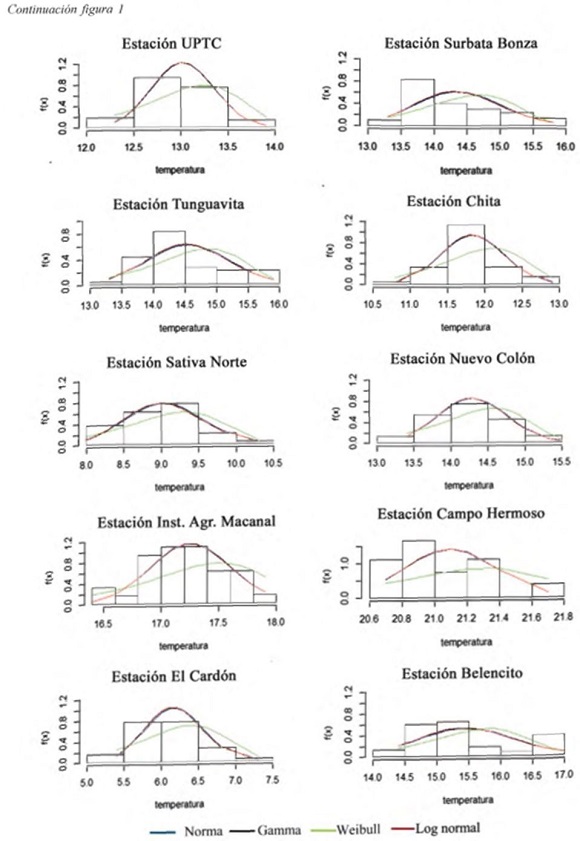
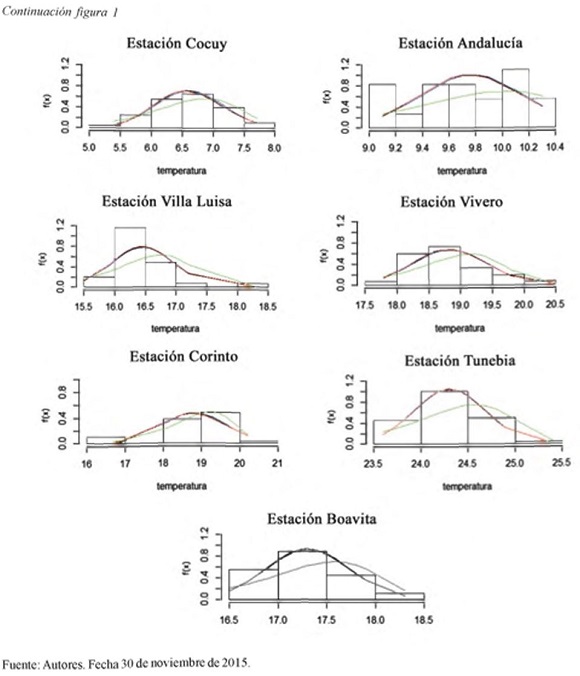
Gráficamente las distribuciones Normal, Gamma y Log normal presentan comportamientos muy similares para la variable temperatura media; la distribución Weibull difiere de estos comportamientos tanto gráficamente así como cuando se aplican los criterios AIC y BIC, tal como se puede apreciar en la figura 1.
El ajuste según el logaritmo de la función de máxima verosimilitud muestra que distribución Weibull es la más adecuada en la mayoría de las estaciones seguida de las funciones Normal y Gamma.
Los métodos propuestos en el presente trabajo permiten ajustar y determinar de manera sencilla distribuciones probabilísticas continuas aplicadas a la variable de temperatura media, pemutiendo futuras estimaciones y proyecciones de la variable en condiciones de mcertidumbre.
El 60 % de las estaciones presentan un ajuste a la distribución Weibull, el cual puede estar basado en la versatilidad de dicha función, la cual puede adoptar diferentes formas según sus parámetros.
Las estaciones con menor cantidad de datos tienden ajustarse a distribuciones diferentes a la Weibull, por el contrario cuando las estaciones
presentan mayor cantidad de datos estas se ajustan mejor a la función de probabilidad Weibull
El tamaño de la muestra influye directamente en la confiabilidad de los datos en el cual se trabajo con un mínimo de 18 y un máximo de 60 años para las estaciones analizadas.
Acuña, C, JA.; Dominguez, C., A.II; Toro. O., E.M 2012 Una comparación entre métodos estadísticos clásicos y técnicas mctahcurísticas en el modclamicnto estadístico. ScicntiactTcchmcaAño XVII. No 50, Abril de 2012. Um\ersidad Tecnológica de Pereira ISSN 0122-1701
Akaike H. 1974 A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), pp 716-723
Akaike H. 1978 A Bayesian analysis of the minimum AIC procedure. The Annals of Statistics. 30( I), pp 9-14, 1978.
Aristi/abal. R J. 2012. Estimating the parameters of the three-parameter lognormal distribution. Flonda International University. FIU Electronic Theses and Dissertations Paper 575
Ayodele. T.R ; Ogunjuyigbe. A.S.O. 2015 Prediction of monthly a\cragc global solar radiation based on statistical distribution of clearness index Energy 90 pp 1733-1742.
Bchar. G. R ; Grima. C. P. 2004 55 Respuestas a dudas típicas de estadística Ediciones Diaz de Santos. S. A.
Bozdogan. H. 1987 Model selection and Akaikc‘s information criterion (AIC) The general theory and its analytical extensions. Psychomctrika. 52( 3). pp 345-379. 1987.
Caballero. D, F.F. 2011. Selección de modelos mediante criterios de información en análisis factorial. Aspectos teóricos y conipuiacionalcs Tesis Doctoral Universidad de Granada Departamento de Estadística c 1.0 ISBN 978-84.694-5742-9.
Chaouchc. K.; Ncppcl. L.; Diculin. C.: Pujol. N.; Ladouchc. B.; Martin. E.; Salas. D.; Caballero. Y. 2010. Analy ses of precipitation, temperature and evapotranspiration in a French Mediterranean region in the context of climate change. C R. Geoscience 342. 234-243.
Donat. M.G.; Alexander. L.V. 2012. The shifting probability distribution of global day time and nighttime temperatures GEOPHYSICAL RESEARCH LETTERS, VOL. 39, LI4707, doi:IO,1029/ 20I2GL052459, 2012
Dorado. D, J ; Burbano, C, J.C.; Molina. T., J.M.; Carvajal. E„ Y.; Aristizábal. H.F. 2006 Ajuste de modelos probabilísimos para cl estudio de la variabilidad espacio-temporal de la precipitación: caso de estudio sistema Sara-Brut Meteorología Colombiana No. 10 pp 60-75. Marzo 2006. ISSN 0124-6984
Hingray. B.; Mczghani, A.; Buishand. T. A. 2007 Development of probability distributions for regional climate change for uncertain global mean warming and uncertain scaling relationship Hydrology & Earth Systems Sciences. 11(3). pp 1097-1114
Kendall. M.G. 1975. Rank Correlation Methods. 4th edition. Charles Griffin. London
Mann. H.B. 1945. Non-paramctnc tests against trend. Economctrica 13, pp 163-171
Martinez, F. L. Métodos de inferencia para la distribución Wcibull: aplicación en fiabilidad industrial Trabajo fin dc master Master en Técnicas Estadísticas Universidad dc Vigo
Minka,T. P. 2002 Estimating a Gamma distribution Microsoft Research. Cambridge. UK. Tech. Rcp
Montesinos,L . A. 2011. Estudio del AIC y BIC en la selección dc modelos dc v ida con datos censurados Tesina dc Maestría Centro dc Investigación en Matemáticas. A C Guanajuato. Gto
Moreno. R. S, Aguilar. A R, Hernández. E F..& Soto. F. P. 2011. Aplicaciones dc la distribución wcibull en ingeniería dc conftabiltdad Memoria del XXI Coloquio Mexicano dc Economía Matemática y Ecoiiomciría. p. 148
Navarrctc. L, C.F. 2008. Distribuido dc probalulidadc c diiiicnsioiiamcnto amostral para tamañito de partícula cm gramíneas forrageiras. Teses dc Mcstra Univcrsidadcdc Sdo Paolo Escola Superior dc Agricultura Luiz dc Quciroz
Ramírez, A. S. 2000. Criterios para la selección dc modelos estadísticos. Banco Central dc Costa Rica Dl E-NT-07-00
Räisänen. J. 2009. Probability distributions of monthlv -to-annual mean temperature and precipitation in a changing climate (CES Climate Modelling and Scenarios Deliverable D2 4. task I) Department of
Physics. P.O. Box 48. FI-00014 University of Helsinki. Finland. AVAILABLE FROM: http://www.atm.helsinki.fi/~jaraisan/CES_D2.4/CES_D2.4_task1.html
Schwarz. G. 1978. Estimating the dimension of a model The Annals of Statistics. 6(2), pp. 461-464.