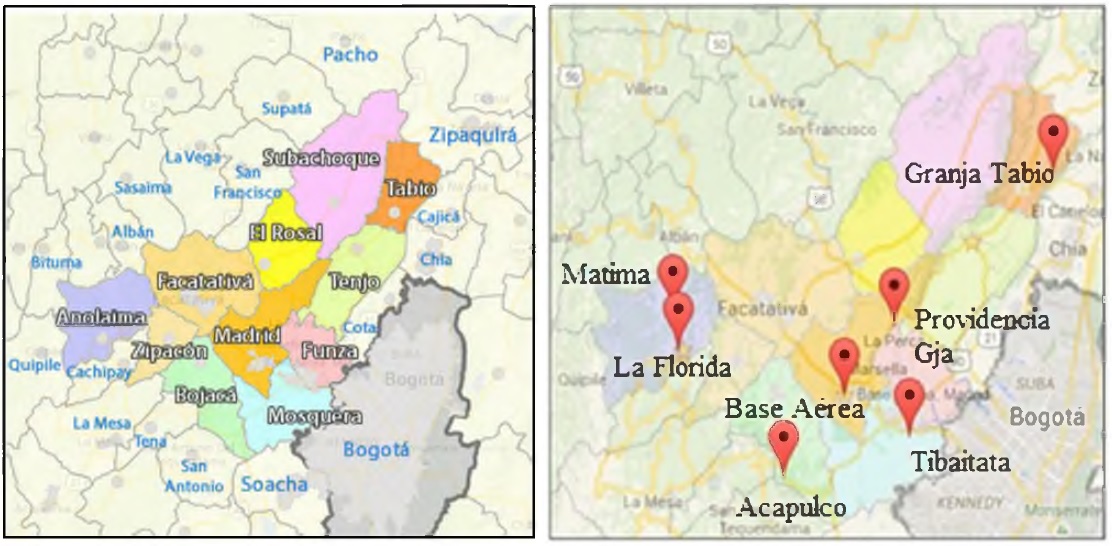
Figura 1. Definición del área de estudio y ubicación de estaciones. Fuente: Autores. Fecha: 31 de julio de 2015.
|
|
|
|
Jazmín Andrea Becerra Oviedo1, Liza Fernanda Sánchez Mazorca2,
Pedro Mauricio Acosta Castellanos3 y José Luis Díaz Arévalo4
Resumen
En este trabajo se presenta la regionalización de las curvas de intensidad-duración y frecuencia a partir del uso de diferentes modelos hidrometereológicos, tomando como área de estudio la Sabana Occidental del departamento de Cundinamarca-Colombia. Para esto, se realiza el respectivo cálculo de las curvas IDF a partir del análisis de las intensidades registradas en los pluviógrafos de siete estaciones meteorológicas ubicadas en la región, se utiliza el método de Gumbell y las respectivas pruebas de bondad de ajuste. Se aplican diferentes técnicas como la regresión lineal y la determinación de los coeficientes de correlación para la interpolación de las intensidades y los parámetros alfa y U. En la regionalización de las intensidades para la zona de estudio, se aplica un método estadístico basado en la correlación lineal de las intensidades en función de las variables topográficas de la región (altitud, latitud y longitud). En este caso se analizan las diferencias encontradas usando como elementos de interpolación las intensidades registradas y los parámetros Alfa y u
Palabras clave: Intensidad; interpolación; regionalización; IDF; Período de retorno.
Abstract
The regionalization of intensity-duration-frequency (IDF) curves is presented in this work through the use of different hydrometeorological models. This regionalization is built in the area of Western Sabana of Cundinamarca department in Colombia. For this, the calculation of IDF curves are made from the analysis of the intensities recorded in seven pluviographs of meteorological stations in the region; the Gumbell method and the respective goodness fit test is used. Different techniques are applied such as linear regression and determining correlation coefficients for intensities interpolation, and the alpha and U parameters. To the intensities regionalization in the area is applied statistical method based on linear correlation of the intensities, depending on the topography of the region variables (altitude, latitude and longitude). In this case the differences are analyzed using the registered elements of intensities and the parameters Alfa and U.
Key words: Intensity; interpolation; regionalization; IDF; return period.
1. Introducción
El objetivo de este trabajo es presentar una metodología para la estimación de lluvias en zonas donde no existe información de pluviosidad o la información existente es insuficiente y, así poder estimar los caudales de diseño necesarios en la planeación de obras hidráulicas. En cuanto al estado del arte se tienen diferentes propuestas entre las cuales Caamaño Nelli, et. al., 2010 en su trabajo sobre lluvia de diseño sin atenuación de datos locales para una cuenca, evalúan las precipitaciones medias de la región para obtener el nivel de inundación a partir de la lluvia de diseño; por otra parte, debido a la escasez de información Catalini Carlos, etal., 2005 trabajan con una metodología que realiza el análisis de superficies tendenciales para generar mapas temáticos que permite salvar el inconveniente típico de información puntual de base, este modelo originalmente fue desarrollado para la transposición en función de una red de polígonos de Thiessen, la cual permitía su extrapolación sobre el área de cobertura. En la tesis de maestría desarrollada por Ganancias, 2010 sobre metodologías de regionalización hidrológica en la región Sur - oeste de la provincia de Córdoba (Argentina), se estudian las características de homogeneidad regional tomando datos de nueve estaciones divididas en dos partes; para el estudio de las características de homogeneidad se siguió el procedimiento de los trazos multidimensionales desarrollado en Andrews, 1972. Mendez, et. al., 2011 proponen una metodología que se basa en el uso de información de las estaciones pluviométricas en la región y, la utilización de curvas IDF de una estación en un lugar con comportamiento hidrológico semejante a la zona de estudio.
La documentación sobre el tema en Colombia muestra el trabajo realizado por Pulgarín, 2009, titulado “Fórmulas regionales para la estimación de curvas intensidad-frecuencia y duración basadas en las propiedades de escala de la lluvia Región Andina Colombiana”, en el que los resultados demuestran que las metodologías basadas en la propiedad de escalamiento simple, estiman de mejor manera las curvas IDF. En dicho trabajo se utiliza un modelo un poco más elaborado desde el punto de vista teórico basado en la invarianza de la lluvia, hasta llegar a teorías poco usadas como las funciones estables, pero que describen de mejor manera el comportamiento de sistemas altamente variables. En el trabajo de Acosta y Caro, 2009 se presenta la regionalización de parámetros hidrológicos para intensidades medias de precipitación para la ciudad de Tunja. Aristizabal, 2009 realizó la estimación de curvas IDF sólo para registros diarios (24 horas) empleando la función de distribución generalizada de valor extremo (GEV), y la estimación de los parámetros con la metodología de los L-momentos tanto para la simulación de control como para los escenarios de cambio climático. Campos, 2013 en su trabajo de grado “Construcción de Curvas IDF, Mediante Interpolación y Parámetros de ajuste, AXplicación al Departamento de Boyacá, Colombia”, comparó el método simplificado con los parámetros de ajuste aplicados que permitan la regionalización de Curvas IDF. En este trabajo se hace uso del método de momentos ordinarios y el método de parámetros, del que se concluye que el primero presentó mayores porcentajes de error comparados con las estaciones de Tunja, y el método de parámetros concluye que se requiere mayor complejidad matemática.
2. Metodología
Este trabajo se realizó sobre la provincia de Sabana Occidente ubicada en la parte centro - occidente del Departamento de Cundinamarca (Figura 1). Se partió de la información proporcionada por el Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia (IDEAM) de los municipios: Anolaima, Madrid, Tabio, Tenjo, Bojacá, Mosquera; que cuentan con sus respectivos pluviógrafos.

Figura 1. Definición del área de estudio y ubicación de estaciones. Fuente: Autores. Fecha: 31 de julio de 2015.
La información se seleccionó teniendo en cuenta el tipo, cantidad y la continuidad de los datos, además de que fueran municipios con cierta cercanía entre ellos, tomando como referencia de análisis el periodo comprendido entre los años 1986 y 2007. Sin embargo, en las estaciones seleccionadas, se encontró que las bandas pluviográficas presentaban registros defectuosos, por el paso del tiempo, lo que llevó a seleccionar aquellos años que tuvieran una información pluviográfica más completa.
Tabla 1. Estaciones Pluviográficas seleccionadas
| Código | Estación | Municipio |
|---|---|---|
| 21205670 | Florida La | Anolaima |
| 21205770 | Base Aérea | Madrid |
| 2120163 | Granja Tabio | Tabio |
| 21205980 | Providencia Gja | Tenjo |
| 21206280 | Acapulco | Bojacá |
| 21205420 | Tibaitata | Mosquera |
| 21206180 | Matima | Anolaima |
Fuente: Catálogo red estaciones hidroclimaticas - IDEAM.
Se analizaron los aguaceros por estación observados entre los años 1986 y 2007. Luego de extraer las precipitaciones máximas diarias para cada uno de los años, se hizo un balance y se agruparon las precipitaciones máximas anuales de cada una de las duraciones, para su respectivo año.
Para la determinación de los parámetros requeridos se emplean los métodos de Momentos Ordinarios (OM) y el método de Máxima Verosimilitud (ML); para ello se utilizan las siguientes expresiones y de acuerdo con esto los parámetros de escala y ubicación (α y μ) se evaluaron, aplicando los ajustes de probabilidad correspondientes (Segerer y Villodas, 2006).
Método de momentos ordinarios (OM):
donde:
Sx = Desviación estándar.
α= Parámetro de escala.
donde
u = Parámetro de ubicación
X̄ = Media.
Luego se reordenan los datos de precipitación de mayor a menor para cada una de las intensidades en las diferentes estaciones.
El periodo de retorno de un evento con una magnitud dada puede definirse como el intervalo de recurrencia promedio entre eventos que igualan o exceden una magnitud especificada. Conforme a lo anterior, la probabilidad de que el evento suceda en cualquier año se da así:
Para este trabajo se adoptaron periodos de retorno de 2, 5, 10, 20, 50, 100, 150 y 300 años respectivamente. El periodo de retorno, también se define como el tiempo promedio en que se vuelve a presentar un evento hidrológico, es decir, la inversa de la frecuencia de que se presente la lluvia de diseño en un determinado intervalo de tiempo.
El planteamiento de los periodos de retorno para la construcción final de las curvas IDF, se desarrolló para las distribuciones de EVI-GUMBEL. Los parámetros se estiman como se muestra en las ecuaciones (1) y (2), donde u es la moda de la distribución (punto de máxima densidad de probabilidad). Una variable reducida Yt, puede definirse como la relación entre la probabilidad y el periodo de retorno, y está conceptualizada para esta distribución, así:
Se determina Yt, que es la variable de Gumbel para el periodo de retorno T y se obtiene a partir de la ecuación 4.
Para la distribución EVI, XT se relaciona con Yt mediante la ecuación:
donde
μ = Parámetro de ubicación.
α = Parámetro de escala.
Yt = Variable reducida.
Se ejecuta la prueba de bondad de aj uste basado en el método se Smirnov-Kolmogorov teórica y empírico. En la primera de estas se determina el coeficiente como:
Donde alfa y beta se obtuvieron anteriormente para cada duración y x corresponde al valor ordenado de mayor a menor de cada una de las intensidades. Con la forma empírica, el coeficiente para evaluar la bondad de ajuste es:
Donde m corresponde a la posición del dato una vez se ordenan de mayor a menor y n es el número total de años evaluados (Aguilera, 2007)
Se determina la desviación (Δ) de los coeficientes calculados anteriormente.
Se compara la desviación máxima con el tolerable (proveniente de tablas), a partir del cual se determina si se acepta o no el ajuste, A-Aceptado, R-Rechazado (Aguilera, 2007). Cabe resaltar el hecho de que el ajuste fue aceptado para todas las estaciones. Por último, y una vez aceptado el ajuste, se procede a graficar las curvas IDF.
Para la regionalización de las curvas IDF se utilizaron diferentes metodologías para interpolar las intensidades y los parámetros alfa y U (interpolación por regresión lineal múltiple, interpolación por la distancia inversa ponderada IDW, interpolación por Kriging, interpolación por Spline), siendo la interpolación IDW la que mejor resultados dio.
3. Resultados
Los resultados de las curvas obtenidas son producto de un muestreo que en algunas ocasiones demandó más de 3 repeticiones, debido a que no era posible un modelo gráfico que representase adecuadamente las curvas IDF, para las 7 estaciones en estudio.
En la figura 1 se observa la estimación de curvas IDF de la estación Base aérea de Madrid Cundinamarca. Se contó con un registro de 22 años comprendido desde 1986 a 2007. Para ello se eligieron un promedio de 3 a 5 eventos máximos anuales para su respectivo análisis de intensidades máximas. Este gráfico se elaboró mediante la distribución de Valor Extremo Tipo I, Gumbel, mediante la estimación de parámetros μ y α por el método de Momentos Ordinarios (OM).
En las curvas podemos observar que las intensidades varían poco con las frecuencias y esto se debe a que el valor de la desviación estándar cuando se incrementa la duración de las lluvias disminuye. Es decir que, con el transcurso de los años, la variación o la dispersión de los datos referentes a las intensidades no son tan variables para duración largas respecto a duraciones cortas, lo que genera en ultimas que los mayores cambios en las intensidades máximas para diferentes frecuencias se visualicen en las duraciones cortas y en esta medida se vaya reduciendo con el incremento de las duraciones.
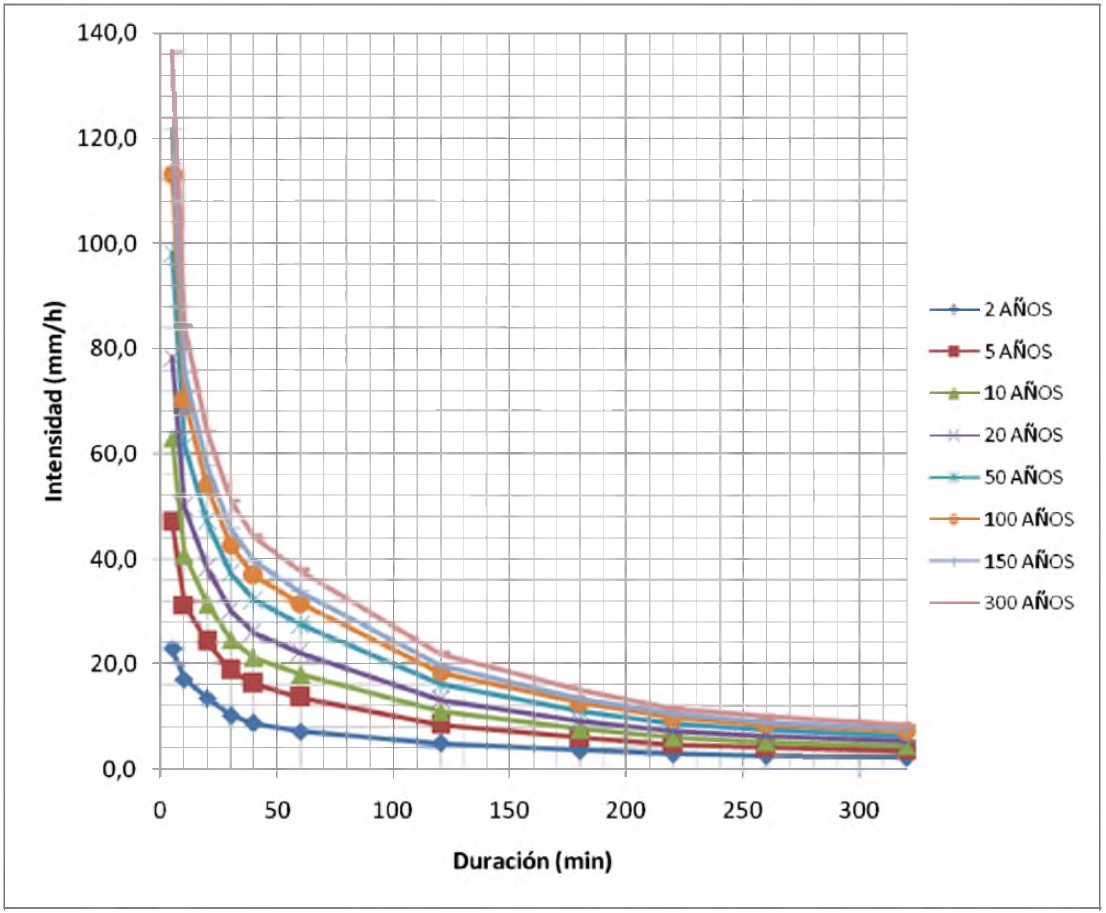
Figura 2 Curvas IDF. EVI-OM. Estación Base Aérea, Madrid Cundinamarca. Fuente: Autores. Fecha: 30 de abril de 2015.
Interpolación usando IDW
La primera técnica implementada usando el software Arcgis es la de DISTANCIA INVERSA PONDERADA por sus siglas en ingles IDW (Inversed Distance Weighted), en la que se usaron los datos de intensidades máximas para un periodo de retorno de 2 y 300 años y una duración de 5 min.
Con esta herramienta se puede cambiar el valor llamado potencia o (Power) que es el que determina que tan detallados van a ser los resultados obtenidos. Cuando se usa un valor de potencia elevado, mayor es el enfoque o apreciación sobre los puntos más cercanos a la región analizada de estudio, más la superficie comparada con los puntos lej anos tendrá una apreciación irregular.
Si se utiliza un valor de potencia menor, se le proporciona más importancia a los puntos que se encuentran más distante a la región de estudio y la superficie tendrá un área suavizada. En el presente trabajo de utilizó un valor de potencia de “2”, puesto que es un valor conservador que es utilizado generalmente por defecto puesto que no se va a ninguno de los límites.
Se definió el área de estudio y la posición geográfica de cada una de las estaciones analizadas a partir de la definición de las características fisiográficas en un archivo Excel, el cual se importa desde Arcgis. Una vez realizado la definición de la zona de estudio, se configura los parámetros de interpolación IDW.
A partir de la información de la Figura 3 y Figura 4, se realiza la comparación entre el valor verdadero de alfa
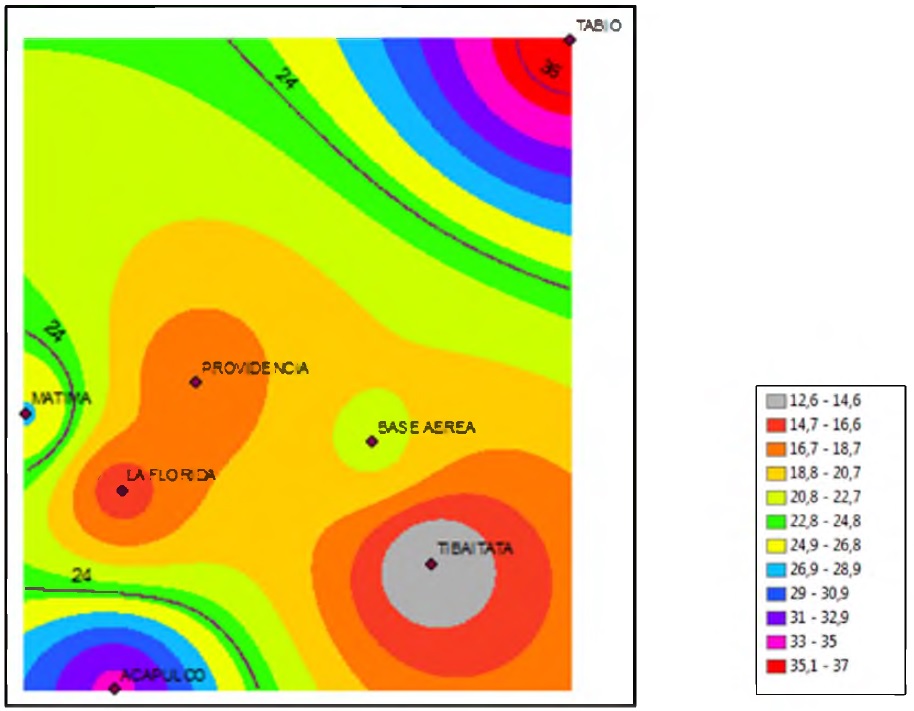
Figura 3. Interpolación alfa usando IDW para D=5 min. Fuente: Autores. Fecha: 31 de julio de 2015.
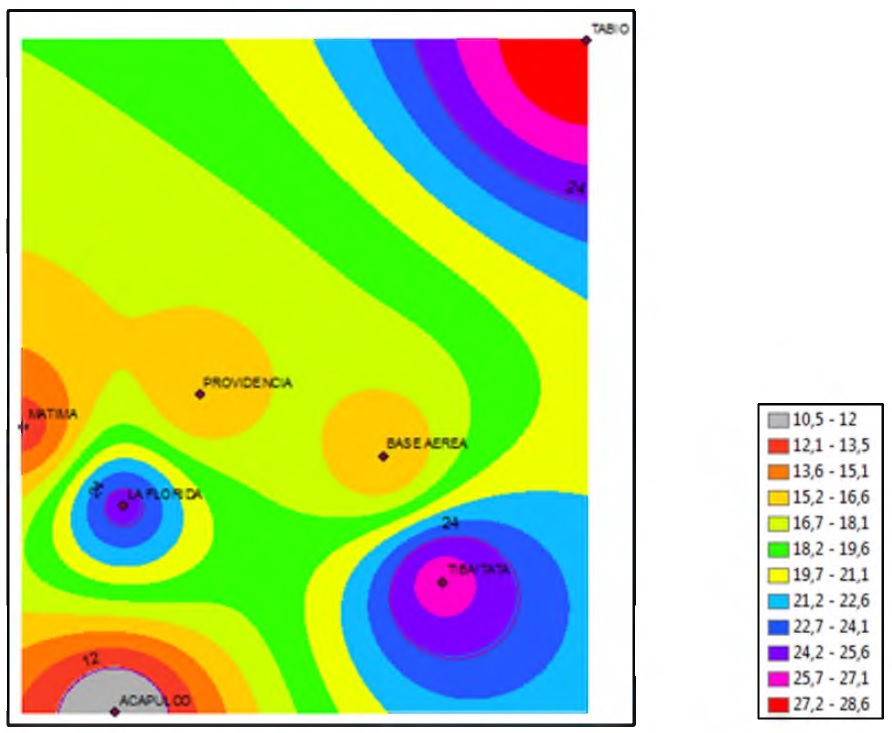
Figura 4. Interpolación u usando IDW para D=5 min. Fuente: Autores. Fecha: 31 de julio de 2015.
y u respecto a la aproximación obtenida con el método IDW, en el que se toma el valor promedio para el cálculo de las precipitaciones.
Tabla 2. Interpolación usando IDW
| Real | |||
|---|---|---|---|
| Nombre | alfa | u | Intensidad [mm/h] |
| ACAPULCO | 33.33 | 10.53 | 22.75 |
| BASE AEREA | 21.26 | 15.17 | 22.96 |
| LA FLORIDA | 15.64 | 24.56 | 30.29 |
| MATIMA | 26.98 | 12.96 | 22.85 |
| PROVIDENCIA | 16.95 | 15.29 | 21.50 |
| TABIO | 37.00 | 28.61 | 42.17 |
| TIBAITATA | 12.56 | 26.33 | 30.93 |
| Aproximado-IDW | Error | Error | ||
|---|---|---|---|---|
| Alfa | u | Intensidad [mm/h] | [mm/h] | relativo [%] |
| 34.00 | 11.25 | 23.71 | 0.97 | 4.25 |
| 20.75 | 15.90 | 23.51 | 0.54 | 2.37 |
| 17.70 | 24.90 | 31.39 | 1.10 | 3.61 |
| 27.90 | 12.80 | 23.03 | 0.18 | 0.78 |
| 17.70 | 15.90 | 22.39 | 0.88 | 4.12 |
| 36.05 | 27.90 | 41.11 | 1.06 | 2.51 |
| 13.60 | 26.40 | 31.38 | 0.45 | 1.46 |
Fuente: Autores. Fecha 31 de Julio de 2015
Tabla 3. Interpolación usando IDW para TR 300 años y DR=5 min
| Real | |||
|---|---|---|---|
| Nombre | alfa | u | Intensidad [mm/h] |
| ACAPULCO | 33.33 | 10.53 | 200.58 |
| BASE AEREA | 21.26 | 15.17 | 136.40 |
| LA FLORIDA | 15.64 | 24.56 | 113.74 |
| MATIMA | 26.98 | 12.96 | 166.80 |
| PROVIDENCIA | 16.95 | 15.29 | 111.94 |
| TABIO | 37.00 | 28.61 | 239.59 |
| TIBAITATA | 12.56 | 26.33 | 97.95 |
| Aproximado-IDW | Error | Error | ||
|---|---|---|---|---|
| Alfa | u | Intensidad [mm/h] | [mm/h] | relativo [%] |
| 34.00 | 11.25 | 205.12 | 4.54 | 2.26 |
| 20.75 | 15.90 | 134.22 | 2.18 | 1.60 |
| 17.70 | 24.90 | 125.83 | 12.09 | 10.63 |
| 27.90 | 12.80 | 171.89 | 5.09 | 3.05 |
| 17.70 | 15.90 | 116.83 | 4.89 | 4.37 |
| 36.05 | 27.90 | 233.46 | 6.13 | 2.56 |
| 13.60 | 26.40 | 103.95 | 6.00 | 6.13 |
Fuente: Autores. Fecha: 31 de julio de 2015.
Se obtiene un error relativo máximo de 4.25% sobre el valor real de la intensidad y un error máximo de 1.1 mm/h. Al comparar dichos porcentajes con los de la interpolación analítica de parámetros (12% aproximadamente) e intensidades (12.5%) se tiene que se presenta mejores resultados.
El máximo porcentaje de error equivale a 10.63% y una diferencia máxima de 12.09 mm/h. De acuerdo con esto, la interpolación que presenta mejores resultados es la IDW si se compara respecto a las otras metodologías analíticas descritas.
4. Conclusiones
5. Referencias bibliográficas
Acosta, P. & Caro, C., 2009. Regionalización de parámetros hidrológicos. Aplicación para intensidad media de precipitación. Tunja: Universidad Santo Tomás, Seccional Tunja. Ponencia.
Aguilera, M., 2007. Estimación de funciones de distribuciones de probabilidad para caudales máximos en la región del Maule. Trabajo de grado. Universidad de Talca. Facultad de ciencias forestales. Escuela de ingeniería forestal.154pp.
Andrews. 1972. 1972. “Plots of high-dimensional data”. Estados Unidos: Bell Telephone Laboratories, Murray Hill, New Jersey and Princeton University. 28: 125 a 136.
Aponte, S.; L. X. 2012. Evaluación de 4 metodologías para la construcción de curvas Intensidad, Duración y Frecuencia. Tunja: s.n.
Caamaño N, G.; C. M. Dasso; A. Rico y L. Colladon, 2010. Una aproximación de tres parámetros a la relación intensidad-duración-recurrencia de lluvias máximas. III Congreso Internacional sobre Gestión y Tratamiento Integral del Agua . Fundación ProDTI (Sevilla, España) y Politécnico Jaime Isaza Cadavid (Medellín, Colombia).
Caamaño N, GE; Joquera, E; Catalini, C.G; Colladon, L; 2011“Lluvia de Diseño para una cuenca: Alternativa de predicción sin atenuación de datos locales” Congreso Nacional del Agua. CONAGUA 2011. Resistencia, Chaco del 22 al 25 de mayo. Comité Permanente de los Congresos del Agua. Rep. Argentina.
Caamaño, N. 2010. Regionalización de Parámetros de un método para pedicción de lluvias máximas. Argentina: Primer Congreso Internacional de Hidrología de Llanuras.
Campos, L. F. y Hernández, J. D. 2013. Construcción de curvas IDF, mediante interpolación de intensidades y parámetros de ajuste, aplicación al departamento de Boyacá Colombia. Boyacá, Universidad Santo Tomás Seccional Tunja. Tunja: s.n. Trabajo de grado para optar por el título de ingeniero civil.
Catalini Carlos, G., y otros. 2005. Implementacion De Una Técnica De Regionalizacion De Láminas Máximas Diarias Y Curvas I-D-T En Las Provincias De Córdoba Y Santa Fe.
Ganancias, F.M.. 2010. Evaluación de Metodologías de Reginalización Hidrológica: Aplicación a los caudales Máximos de Cuencas Representativas de la región Sur - Oeste de la Provincia de Córdoba. Universidad Nacional de Córdoba. Cordoba, Argentina: s.n. Tesis de Maestría .
Méndez, J.; Návar, J. y González, V. 2008. Análisis de tendencias de precipitación (1920-2004) en México. México: Universidad Autonoma de México.
Méndez, J. Mesa, O., y otros. 2001. Regionalización de Características Medias de la Cuenca con Aplicación en la estimación de caudales máximos. Medellín: s.n.
Pulgarín, E. G.. 2009. Formulas regionales para la estimación de curvas intensidad - Frecuencia- Duración basadas en las propiedades de escala de la Lluvia (Región Andina Colombiana). Tesis de Magister. UNIVERSIDAD NACIONAL DE COLOMBIA. Medellín.
Segerer, C y Villodas, R. 2006. Hidrología I: Las precipitaciones. Universidad Nacional de Cuyo Facultad de Ingeniería Ingeniería Civil.