En los problemas clásicos de flujo en tuberías se presentan dos situaciones típicas en las que el analista busca determinar el caudal (Q) o el diámetro de diseño (F); estos han sido tradicionalmente resueltos mediante procesos iterativos sobre el factor de fricción (D) tratando de hallar una variable que no es propiamente la incógnita principal del problema, con el ánimo aparente de facilitar la solución y sacar del paso los cálculos en derivadas que implica una solución más real. En este artículo, se presenta una propuesta de una nueva formulación para este problema basada en una fundamentación numérica que encuentra directamente las variables de interés, adaptando matemática y computacionalmente el método de Newton Raphson el cual converge rápidamente a la solución deseada. Se desarrolló una aplicación educativa en Java, mediante su IDE Netbeans. Los resultados encontrados llaman la atención de la forma como tradicionalmente se enseña a resolver los problemas de flujo en tuberías en los textos clásicos de la mecánica de los fluidos.
Palabras clave: Flujo Laminar, Flujo Turbulento, Tuberías, Ecuación de Colebrook, Ecuación de Darcy-Weisbach, Método de Newton Raphson.
Contained in the classic problems of pipeline flow, there are two standard situations in which the analyst seeks to find the flow(0 or the diameter design (F). The results have traditionally been obtained through iterative processes that try to obtain the friction factor (D) by endeavoring to discover a variable that is not, in itself, the principal unknown problem. The purpose of this is to facilitate finding the solution by not having to calculate derivatives, which, consequently leads to a solution that is more real. In this article a proposal is presented for a new formulation for this problem, based on a numerical foundation that can directly find the variables of interest, mathematically and computationally adapting the Newton Raphson Method, which quickly finds the desired solution. An educative application using Java has been developed that uses Netbeans IDE. The results obtained question the form in which, traditionally, we are taught to resolve liquid flow in pipeline problems using classic fluid mechanics texts.
Key words: Laminar Flow,Turbulent Flow, Pipelines,The Colebrook Equation,The Darcy-Weisbach Equation, The Newton Raphson Method.
En el diseño o análisis de sistemas de tuberías existen seis variables involucradas, excluyendo la aceleración de la gravedad (g), que es considerada constante para cualquier sistema de tuberías (Franzini, 1999).
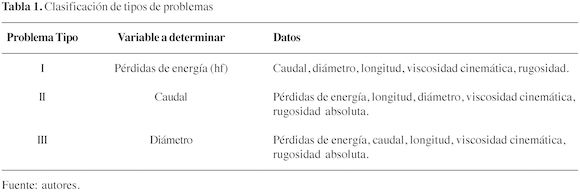
En la práctica es de interés para el analista determinar una de los tres primeras variables, mientras que los demás se conocen o pueden ser determinadas por el diseñador. En función de la incógnita a determinar, se definen tres clases de problemas, estos se resumen en la tabla 1 (Mott, 1996).
Los sistemas clase I se solucionan de manera explícita y secuencial con un número definido de pasos, por tanto no reviste interés, mientras que los Tipo II y Tipo III se solucionan mediante métodos iterativos (Palacio, 2008). Sin embargo, comúnmente se han solucionado los sistemas Tipo II y Tipo III, a través de iteraciones sobre el factor de fricción, es decir tratando de hallar una variable que no es directamente la incógnita principal (Pérez, 2013). Es por esto que los autores de este artículo han desarrollado una nueva formulación, basada en una nueva visión numérica de la solución de dichos sistemas, que busca, adaptando el método de Newton Raphson, hallar directamente las variables incógnitas para cada uno de los casos caudal (Q) y diámetro (D) respectivamente (Burden, 1998). En muchos textos de mecánica de fluidos es común encontrar las metodologías para sistemas clase II y clase III basadas en la iteración del factor de fricción/, de tal manera, que se hace justificable implementar la nueva metodología, ya que, es más racional y eficiente para la solución de dichos sistemas con algunas bondades heredadas del método Newton-Raphson (Terreros, 2015).
Por requerir de una explicación ampliada se describe a continuación la formulación matemática empleada para la solución de los problemas clase II y clase III.
El modelo matemático se funda en las fórmulas de Colebrook y Darcy-Weisbach descritas en las ecuaciones (1) y (2) respectivamente (Flechas ,2012).
En la ecuación (1) la variable Re representa el número adimensional característico de los problemas de flujo en tuberías denominado número de Reynolds sobre el cual se precisan detalles más adelante (Giles, 1994). La ecuación (3) que se obtiene de la ecuación (1) permite calcular el coeficiente de fricción cuando se desconoce el caudal (Q); para esta situación se asume turbulencia completa que conduce a un valor despreciable del segundo término del paréntesis de (1) donde interviene el número de Reynolds Re (Pérez, 2013).
En el problema tipo II el método requiere de un valor semilla para inicializar el proceso iterativo, por lo cual, utilizando la ecuación (2) y reemplazando las expresiones (4) y (5) en dicha ecuación, se obtiene el caudal semilla descrito por la ecuación (6).
a continuación se evalúa a partir del caudal semilla Qo el número de Reynolds Re descrito en la ecuación (7)
Si el número de Reynolds es menor de 2000 el flujo se considera laminar y es posible calcular la fricción a partir de la ecuación (8) propuesta por Poiseuille en 1846 (Rodríguez, 2004).
Si el flujo es turbulento (Re?4000) es posible calcular el factor de fricción/a partir de la ecuación explícita (9) con un error alrededor del 1 % con respecto a la ecuación de Colebrook (3).
La ecuación (9) tiene validez dentro de ciertos rangos de e/D y Re definidos en las expresiones (10) y (11).
La ecuación (12) obtenida de la acomodació conveniente de la ecuación (6) es la funció utilizada para resolver el problema caudal; esta ecuació proviene de reemplazar las ecuaciones (4) y (5) en la ecuació (2) de Darcy-Weisbach e igualar a cero.
Conocida la función objetivo se procede a solucionarla. Se sabe que el método de Newton Raphson requiere de la función y su derivada (Palacio,2008), esto significa que la solución del problema puede ser determinada iterando sobre la ecuación (13).
La derivada Z2’ de la función descrita en (13) respecto a Q es altamente compleja por ser implícita y compuesta. La expresión se obtuvo con la ayuda del CAS libre Máxima. El número de iteraciones del proceso de cálculo es aquel que lleva la función a un valor menor o igual a lxlO-14.
Al igual que en el cálculo de caudal, el problema tipo III requiere de un valor semilla del diámetro (D) para iniciar el proceso iterativo. Para establecer este valor se parte de un diámetro arbitrario con el cual se calcula el factor de fricción /utilizando la ecuación (8) o (9) según sea el caso; se despeja el diámetro D de la ecuación (2) previo remplazo de las ecuaciones (4) y (5) y se obtiene el diámetro corregido descrito en la ecuación (14).
La ecuación (14) tiene la ventaja de que el valor inicial del diámetro supuesto inicialmente no tiene que ser cercano al valor real ya que el valor del diámetro corregido siempre será una muy buena aproximación a la solución, por tanto, se requieren pocas iteraciones para obtener resultados satisfactorios. En las iteraciones sucesivas el cálculo del factor de fricción/se realiza usando las ecuaciones (8) o (9) según el caso.
Definido el valor inicial del diámetro o diámetro semilla, se plantea la solución iterativa por medio del método Newton Raphson que requiere de la función y su derivada. La ecuación (15) es la función utilizada. Nótese que siendo Q una constante la función ahora es del diámetro.
La derivada de la función respecto a D además de implícita es compuesta por lo cual se recurrió a la ayuda del CAS libre Máxima. La solución del problema puede ser determinada iterando sobre la ecuación (16).
El número de iteraciones del proceso de cálculo es aquel que lleva la función a un valor menor o igual a lxlO-14.
La formulación del problema descrito se implemento computacionalmente en el lenguaje de programación Java, mediante su IDE Netbeans. La herramienta computacional desarrollada consta de un formulario principal desde el cual se despliegan ventanas utilizadas para introducir los datos y visualizar los resultados.
La validación del problema tipo II se llevó a cabo por medio de un caso típico propuesto en el clásico libro de Mecánica de Fluidos de Streeter en el que se intenta determinar el caudal de agua que se encuentra a 15 oC (n=l.13e-6 m2/s) y que fluye a través de un tubo de acero remachado de 300 mm de diámetro, e=3mm, con una pérdida de cabeza de 6m en una longitud de 300m.
En la Figura 1 se muestra la carga de datos del problema planteado.
La figura 2 muestra los resultados obtenidos de acuerdo al modelo matemático y numérico descrito.
Los resultados de la aplicación mostrados en la figura 2 apuntan a un caudal de 0.1242 m3/s que se encuentra muy cercano a la solución de referencia de 0.1245 m3/s, la cual está basada en el diagrama de Moody y en iteraciones que verifican el valor de/como criterio de parada. Con la aplicación desarrollada no se requiere el uso del diagrama de Moody y es más evidente verificar la solución directamente sobre la variable principal Q.
La validación del problema tipo III también se llevó a cabo por medio de un caso típico propuesto en el clásico libro de Mecánica de Fluidos de Streeter en el que se trata de determinar la medida de un tubo de hierro forjado limpio (e=0.00015 pies) que se requiere para conducir 4000 gpm de aceite (8.93 pies3/s), n= 0.0001 pies2/s), con una pérdida de cabeza de 75 pies en una longitud de 10000 pies.
En la Figura 3 se muestra la carga de datos del problema planteado.
La figura 4 muestra los resultados obtenidos de acuerdo al modelo matemático y numérico descrito.
Los resultados de la aplicación que se muestran en la figura 4 convergen a un valor de diámetro igual a 1,387pies que se encuentra muy cercano a la solución de referencia de 1.382 m3/s, la cual está basada en el diagrama de Moody y en iteraciones que verifican el valor de/como criterio de parada. Con la aplicación desarrollada no se requiere el uso del diagrama de Moody, solo se hace una suposición de D que rápidamente es corregida y usada como semilla; de esta manera, es mucho más intuitivo verificar la solución directamente sobre la variable principal D.
La propuesta metodológica exhibe ventajas frente a la estrategia clásica de iterar el factor de fricción ƒ , dado que, puede determinarse directamente la variable buscada Q o D según sea el caso por medio de un metodología de cálculo basada en un método numérico de muy buena convergencia como Newton Raphson.
En la formulación del método se encontraron grandes posibilidades del software CAS Maxima, para la derivación implícita de funciones muy complejas como las que aparecen al establecer el sistema de ecuaciones compuesto por la ecuación de fricción de Coolebrok, la ecuación del número de Reynolds y la ecuación de pérdidas de Darcy-Weisbach.
El uso de software libre como Maxima y Java, plantea herramientas de excelente alcance para investigaciones en diferentes campos de los métodos numéricos. Estas herramientas poseen bondades de portabilidad que les permite correr con independencia del sistema operativo utilizado.
Las estrategias propuestas de “plantación de semilla” en los dos problemas tipo, son suficientemente buenas para alcanzar resultados satisfactorios en muy pocas iteraciones.
1. Burden R., 1998. Análisis Numérico. 6a Ed.,Thompson Internacional, México.
2. Flechas, R. A., 2012. Efecto del uso de la ecuación de Darcy-Weisbach vs. la ecuación de Hazen Williams en el diseño de redes matrices, XX Seminario Nacional de Hidráulica e Ingeniería Barranquilla, Colombia.
3. Franzini,J. B., Finnemore, E. J., 1999. Mecánica de Fluidos con Aplicaciones en Ingeniería. 9a Ed., McGraw-Hill Interamericana, Madrid, 503 p.
4. Giles, R. V., 1994. Theory and problems of Fluid mechanics and hydraulics, 2a Ed., Schaum Publishing, New York.
5. Mott, R. L., 1996. Mecánica de Fluidos Aplicada. 4° Edición. Prentice-Hall Hispanoamericana, México, 580 p.
6. Palacio, F., 2008. Resolución aproximada de ecuaciones: Método de Nevvton-Raphson, Escuela Politécnica de Catalunya, V. 1.3, España.
7. Pérez, L. E., 2013. Breve historia de la ecuación de Darcy- Weisbach y Consideraciones de interés sobre la misma, Ed. Universidad de Buenos Aires, Argentina.
8. Rodríguez, W., Pallares, M., 2004. Análisis de sistemas de tuberías y tanques mediante el programa de elementos finitos Ansys, XVI Seminario Nacional de Hidráulica e Hidrología, Armenia.
9. Streeter, V. L., Wylie, E. B., 2000. Mecánica de Fluidos. 9a Ed. McGraw-Hill Interamericana, S A., Bogotá, 740 p.
10. Terreros, J. K„ Hidalgo, D. A., Silva, J. F„ 2015. Cálculo de diámetros de tubería mediante la ecuación de Darcy-Weisbach aplicando el método de Newton-Raphson. Universidad Distrital, Bogotá.