Gerson R. Rojas A.1, Andrés F. Rivera1 y Daniel Ricardo Delgado2
En este trabajo se aplicó el método extendido de solubilidad de Hildebrand (MESH) para evaluar la solubilidad de mitomicina C en mezclas etanol + agua a 293,15 K. Se reporta la solubilidad experimental y algunas propiedades de fusión de éste fármaco que fueron utilizados para los cálculos del método extendido de Hildebrand. En particular, EHSA presenta un buen carácter predictivo mediante el uso de un polinomio regular de orden cinco para el parámetro de interacción W en una función del parámetro de solubilidad de mezclas cosolvente libre de fármaco.
Palabras clave: Mitomicina; Etanol; Mezclas binarias; Método extendido Hildebrand; parámetros de solubilidad.
In this work, we applied the extended Hilderband solubility approach (EHSA) to evaluate the solubility of mitomycin C in ethanol-water mixtures at 293.15 K. We report the experimental solubility and some of the drug’s fusion properties that were used for the calculations in the extended Hilderband approach. In particular, EHSA presents good predicative properties by means of a regular fifth-degree polynomial for interaction parameter Win a function of the solubility parameter of solvent mixtures without the drug.
Key words: Mitomycin, etanol; binary mixtures, extended Hildebrand solubility approach; solubility parameters.
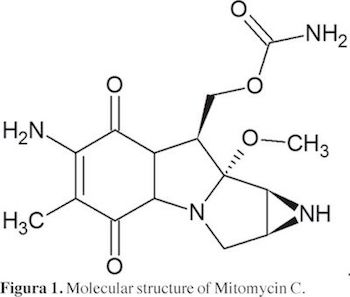
Mitomycin C Fig 1. (C15H18N405, molecular weight 334.33, IUPAC [6-Amino-8a-methoxy-5-methyl-4,7-dioxo-1,1a,2,4,7,8,8a,8b-octahydroazireno[2',3':3,4] pyrrolo[l,2-a]indol-8-yl]methyl carbamate, CAS Registry No.: 50-07-7) (Gandhi and Murthy, 2012) is an antibiotic and anti-neoplastic material isolated from the broth of Streptomyces caespitosus and is one of the naturally occurring antibiotics that was first discovered in 1956 (Hata, etal., 1956). This drug has been demonstrated to have antifibroblastic activity in vitro and in vivo (Unal, 2004). It is an antineoplastic antibiotic that acts as an alkylating agent by inhibiting DNA and protein synthesis. It can inhibit cell division, protein synthesis, and fibroblast proliferation (Rahbar, et al., 2000). Despite the usefulness of these drugs, their physicochemical properties in aqueous solution have not yet studied completely (Budavari, 2001; Gandhi and Murthy, 2012). In particular, it is well known that their solubilities in neat aqueous media are very low (Jouyban, 2010). It is noteworthy that cosolvency is the best technique used in pharmacy for increasing drugs solubility (Rubino, 1988; Yalkowsky, 1999). On the other hand, it is clear that predictive methods of physicochemical properties of drugs, in particular the ones intended to estimate solubilities, are very important for industrial pharmacists because they allow optimizing several design processes (Budavari, 2001; Martin, et al., 1993; Regosz, etal., 1992; Martinez and Gómez, 2002; Hanaee, etal., 2005).
For this reason, this work presents a physicochemical study about the solubility prediction of the mitomycin C, in binary mixtures conformed by ethanol (EtOH) and water at 293.15 K. The study was done based on the Extended Hildebrand Solubility Approach (EHSA) (Martin, et al., 1993; Martin and Bustamante, 1989; Martínez, 2005) by using experimental solubility values and some properties relative to the fusion of these drugs taken from the literature (Gandhi and Murthy, 2012). It is important to keep in mind that EHSA method has been widely used to study the solubility of a lot of pharmaceutical compounds as has been recently exposed in the literature (Holguín, et al., 2012). Furthermore, it is still employed to evaluate the behavior of drugs in several co-solvent mixtures (Sotomayor, et al., 2013; Cristancho, et al., 2013; Gómez, et al., 2013; Rathi, 2011; Dehpande, et al., 2014). On the other hand, it is remarkable that EtOH is one of the more employed co-solvent to develop liquid pharmaceutical dosage forms because of its solubilizing and antimicrobial properties (Smolinske, 1992; Aulton, 2002).
The ideal solubility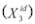 
of a solid solute is calculated by means of the expression,
where, ΔHfus is the molar enthalpy of fusion of the pure solute (at the melting point), Tfus is the absolute melting point, T is the absolute solution temperature, R is the gas constant (8.314 J mol–1 K–1), and ΔCp is the difference between the molar heat capacity of the crystalline form and the molar heat capacity of the hypothetical supercooled liquid form, both at the solution temperature. Since ΔCp cannot be easy experimentally determined, this property may be approximated to the entropy of fusion, ΔSfus. Ideal solubility depends only on the physicochemical properties of the solid compound without considering the properties of the solvent. For this reason the ideal solubility would be higher as the solute-solute inte- ractions are lower (Gandhi and Murthy, 2012). Accordingly, compounds with high values of melting point and enthalpy of fusion have lower ideal solubilities.
On the other hand, the real solubility (X3) of a solid solute in a liquid solution is calculated by means of the expression,
where, log γ3 is the non-ideality term, being γ3 the solute activity coefficient, which is determined experimentally.
Nevertheless, one method of calculating γ3 is the referent to regular solutions obtained from,
where, V3 is the partial molar volume of the solute, φ1 is the volume fraction of the solvent in the saturated solution, and δ1 and δ3 are the solubility parameters of solvent and solute, respectively. φ1 is calculated as,
where V1 is the molar volume of solvent.
Nevertheless, all the pharmaceutical dissolutions deviate of predicted by the regular solutions theory. For this reason, Martin et al. developed the EHSA method (Martin and Carstense, 1980; Martin and Wu, 1981; Martin and Miralles, 1982; Martin, et al., 1981, 1982, 1985). Thus, if the A term (defined as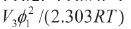 
) is introduced in the Eq. (3), the real solubility of drugs can be calculated from the expression, X3
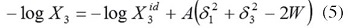
where, the W term is equal to 2Kδ1δ3 (where, K is the Walker parameter (Martínez and Gómez, 2002). The W factor can be calculated from experimental data by means of,
where, γ3 is the activity coefficient of the solute in the saturated solution, and it is calculated as,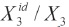 
. The experimental values of the W parameter can be correlated by means of regression analysis by using regular polynomials as a function of d1, as follows,
These empiric models can be used to estimate the drug solubility by means of back-calculation resolving this property from the specific W value obtained in the respective polynomial regression.
The required properties about the mitomycin C studied, like ideal solubility, molar volume and Hildebrand solubility parameter (Table 1), was calculated from the drug thermodynamic data reported previously in the literature (Gandhi and Murthy, 2012); whereas, the volumetric behavior and polarity of EtOH + water mixtures, as a function of the composition, is shown in Table 2 (Gandhi and Murthy, 2012). Volume fractions and Hildebrand solubility parameters were calculated assuming additive behavior (Martin, et al., 1993; Connors, 2002). Table 2 also summarizes the experimental solubility of the mitomycin expressed in mole fraction reported in the literature (Gandhi and Murthy, 2012), including ideal solubility.
Figure 2 shows the ideal and experimental solubility, as well as the calculated solubility by using the regular solution model ,i.e. Eq. (3), as a function of the solubility parameter of solvent mixtures, from 26.5 to 47.8 MPa1/2. In order to use Eq. (3) the molar volume and Hildebrand solubility parameter of the mitomycin C, estimated according to the groups contribution method proposed by Fedors, is 26.70 MPa1/2 Table 1 (Fedors, 1974). It is important to keep in mind that according to regular solutions model the maximum solubility value corresponds to the ideal solubility and it is obtained just when both solubility parameters of drug and solvent mixture are coincident, like it is shown in Fig. 2. On the other hand, according to the literature the maximum experimental solubility values are found when the solubility parameters of both solute and solvent are also coincident (Martin and Bustamante, 1993, 1989). Nevertheless, in the present case the experimental dmg solubilities are lower than the calculated according to Eq. (3) in all the compositions for the mitomycin C.
The φ1 values calculated according to Eq. (4) are almost equal to 1.000 because the solubility of mitomycin C is very low in all the solvent system considered, varies form 0.9997 and 0.9888 in EtOH-rich mixtures due to its high solubility (Table 3). Otherwise, the activity coefficients of mitomycin C expressed as decimal logarithms are also presented in Table 3. This table also summarizes the parameters A, K, and Wfor the mitomycin C in EtOH + water mixtures; whereas, Figure 3 shows that the variation of the W parameter with respect to the solubility parameter of solvent mixtures, presents deviation from linear behavior, just as it is expectable because the W term implies the summation of two quadratic (δ22 and δ22) and one nonconstant-quotient (-log δγ2 / A) terms, as Eq. (6) shows.
W values were adjusted to regular polynomials in orders from 2 to 5 (Eq. 7). Linear equation was also considered just as comparison. Table 4 summarizes the coefficients obtained in all the regular polynomials for the mitomycin. The significant figures in the coefficients and uncertainties were defined according to the criterion 3-30, when that was possible (Shoemaker and Garland, 1968). Briefly, this criterion establishes that the numeric quantity in uncertainty should be placed between 3 and 29, without consider decimal positions, except if they integers greater than 30. In this way the number of decimal places for the coefficients is defined according to the decimal places of the respective uncertainties.
It is found that as more complex the polynomial used is, better the agreement found between experimental and calculated solubility also is. Accordingly, the most important increment in concordance is obtained passing from order 1 to order 2. The concordances also increase in good way from order 2 to 3 and from order 3 to 4. In the last case the mean uncertainties obtained are in the same order or lower than those reported experimentally (Gandhi and Murthy, 2012). It is important to keep in mind that for pharmaceutical purposes uncertainties lower than 5% are useful for practical purposes but for academic purposes best agreements are required. In this way, although an additional improves is obtained by passing from order 4 to 5 this result is not relevant because the mean uncertainties are lower in comparison with those reported for experimental values (Gandhi and Murthy, 2012).
As has been previously described, a very important consideration about the usefulness of the EHSA method is the one referent to justify the complex calculations involving any other experimental variables of solute and solvents, instead of the simple empiric regression of the experimental solubility as a function of the solubility parameters of solvent mixtures as shown in Fig. 3. For this reason, Table 6 shows the coefficients of regular polynomials in order 4 of log X3 as a function of d{ values (Eq. 8). The significant figures in the coefficients and uncertainties were also defined according to the criterion 3-30 (Shoemaker and Garland, 1968).
On the other hand, Table 7 shows the calculated values of solubility by using Eq. (8) in and also the respective difference percentages in front the experimental ones.
Based on mean deviation percentages presented in Tables 5 and 7 it follows that no difference is found between the values obtained by using both methods. These results would show anon-significant usefulness of EHSA method for practical and academic purposes in the case of the mitomycin C studied. Nevertheless, it is necessary keep in mind that this correlative method considers the drug solubility from a systematic physicochemical point of view. Moreover, it would just be necessary to find an effective method to calculate the Walker K parameter in order to calculate the W term according to the expression W = , because the di and d3 terms would be known, and thus, the drug experimental solubility could be calculated in any mixture (Martin and Bustamante, 1989).
In this investigation the extended Hildebrand solubility approach has been adequately used to study the solubility of mitomycin C in ethanol + water mixtures at 293.15 K. In particular, a good predictive character has been found by using a regular polynomial in order five of the interaction parameter as a function of the solubility parameter of solvent mixtures free of drug. Nevertheless, the predictive character of EHSA is the same as the one obtained by direct correlation between mitomycin C solubility and the same descriptor of polarity of the co-solvent mixtures.
1. Aulton ME., 2002. Pharmaceutics, The Science of Dosage Forms Design, 2nd edn., Churchill Livingstone. London.
2. Budavari S., O’Neil M.J., Smith A.,HeckelmanP.E., Obenchain Jr. J.R., Gallipeau J.A.R., D’Arecea M.A., 2001. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals. 13th ed., Merck & Co., Inc, Whitehouse Station.
3. Connors K.A., 2002.Thermodynamics of Pharmaceutical Systems: An Introduction for Students of Pharmacy, Wiley-Interscience, Hoboken.
4. Cristancho D.M., Delgado DR, Martinez F., 2013. Meloxicam solubility in ethanol + water mixtures according to the extended Hildebrand solubility approach. J. Solution Chem. 42:1706-1716.
5. Delgado DR, Martinez F., 2015. Solution thermodynamics and preferential solvation of sulfamerazine in some methanol + water mixtures. J. Solution Chem. 44(2): 360-377.
6. Deshpande K.V., Panzade P.S., Rathi P.B., 2013. Prediction of nabumetone solubility in propylene glycol-water mixtures using extended Hildebrand solubility approach. Inn. Pharm. Pharmacother. 1:117-127.
7. Fedors R.F., 1974. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 14:147-154.
8. P.J., Murthy, Z.V.P., 2012. Measurement of solubility of mitomycin C in ethanol-water solutions at different temperatures. Thermoch. Act., 545. 163-173.
9. Gómez J.L., Rodíguez G.A., Cristancho D.M., Delgado D .R., Mora C .P., Yurquina A, Martínez F., 2013. Extended Hildebrand solubility approach applied to nimodipine in PEG 400 + ethanol mixtures. Rev. Colomb. Cienc. Quim. Farm. 42:103-121.
10. Hanaee J, Jouyban A, Dastmalchi S, Adibkia K, Mirzazadeh A, Barzegarjalali M., 2005. Solubility prediction of sulfonamides at various temperatures using a single determination. DARU, 13:37-45. Aplicación del Método Extendido de Hildebrand... / Rojas A. & C oís.
11. Hata,T., Sano, Y., Sugawara, R., Matsumae, A., Ka-namorei, K., Shima, T., Hoshi, T., 1956. Mitomycin a new antibiotic from streptomyces, J. Antibiot. Ser., 141-146.
12. Holguin A.R., Delgado D.R., Martínez F., 2012. Indomethacin solubility in propylene glycol + water mixtures according to the extended Hildebrand solubility approach. Lat. Am. J. Pharm. 31:720-726.
13. Jouyban A., 2010. Handbook of Solubility Data for Pharmaceuticals, CRC Press, Boca Raton.
14. Martin A., Bustamante R, 1989. El parámetro de solubilidad en las ciencias farmacéuticas. Anal. Real Acad. Farm. 55:175-202.
15. Martin A., Bustamante P., Chun A.H.C., 1993. Physical Chemical Principles in the Pharmaceutical Sciences. 4th ed., Lea & Febiger, Philadelphia.
16. Martin A., Carstensen J., 1981. Extended solubility approach: Solubility parameters for crystalline solid compounds. J. Pharm. Sci. 70:170-172.
17. Martin A., Miralles M.J., 1982. Extended Hildebrand solubility approach: Solubility of tolbutamide, acetohexamide, and sulfisomidine in binary solvent mixtures. J. Pharm. Sci. 71:439-442.
18. Martin A., Newburger J., Adjei A., 1980. Extended Hildebrand approach: Solubility of caffeine in dioxane-water mixtures. J. Pharm. Sci. 69:659-661.
19. Martin A., Paruta A.N., Adjei A., 1981. Extended Hildebrand Solubility Approach: Methylxanthines in mixed solvents. J. Pharm. Sci. 70:1115-1115.
20. Martin A., Wu P.L., Adj ei A., Mehdizadeh M., James K.C., Metzler C., 1982. Extended Hildebrand solubility approach: testosterone and testosterone propionate in binary solvents. J. Pharm. Sci. 71:1334-1340.
21. Martin A., Wu P.L., 1981. Extended Hildebrand solubility approach: p-Hydroxybenzoic acid in mixtures of dioxane and water. J. Pharm. Sci. 72:587-592.
22. Martin A., Wu P.L, Velasquez T., 1985. Extended Hildebrand solubility approach: sulfonamides in binary and ternary solvents. J. Pharm. Sci. 74:277-282.
23. Martinez F., 2005. Utilidad del método extendido de Hildebrand en el estudio de la solubilidad del acetaminofén en mezclas agua-propilenoglicol. Rev. Acad. Colomb. Cieñe. 29:429-438.
24. Martínez F, Gómez A., 2002. Estimation of the solubility of some sulfonamides in aqueous media from partition coefficients and entropies of fusion. Phys. Chem.Liq. 40:411-420.
25. Rahbar, R., Valdez, T., Shapshay S., 2000. Preliminary results of intraoperative mitomycin-C in the treatment and prevention of glottic and subglottic stenosisJ. Voice, 14, 282-286.
26. Rathi P.B., 2011. Solubility prediction of satranidazole in propylene glycol-water mixtures using extended Hildebrand solubility approach. Indian J. Pharm. Sci. 73:670-674.
27. Rathi P.B, Deshpande K.V., 2014. Extended Hildebrand Approach: An empirical model for solubility prediction of etodolac in 1,4-dioxane and water mixtures. J. Solution Chem. 43:1886-1903.
28. Regosz A., Pelpliñska T., Kowalski P, Thiel Z., 1992. Prediction of solubility of sulfonamides in water and organic solvents based on the extended regular solution theory. Int. J. Pharm. 88:437-442.
29. Rubino J.T., 1998. Cosolvents and cosolvency. In: Swarbrick J., Boylan J.C., eds. Encyclopedia of Pharmaceutical Technology. Vol 3, Marcel Dekker, Inc., New York.
30. Shoemaker D.P., Garland G.W., 1968. Experimentos de Fisicoquímica, Unión Tipográfica Editorial Hispano Americana, México.
31. Smolinske S.C., 1992. Handbook of Drug, Food and Cosmetic Excipients, CRC Press LLC, Boca Raton.
32. Sotomayor R.G., Holguin A.R., Cristancho D.M., Delgado D.R, Martínez F., 2013. Extended Hildebrand Solubility Approach applied to the piroxicam solubility in ethanol + water mixtures. J. Mol. Liq. 180:34-38.
33. Unal, M. 2004. The successful management of congenital laryngeal web with endoscopic lysis and topical mitomycin C, Int. J. Pediatr. Otorhino-laryngol. 68, 231-235.
34. Yalkowsky S.H., 1993. Solubility and Solubilization in Aqueous Media, American Chemical Society and Oxford University Press, New York.
