Martín Diomedes Bravo1, Daniela Trujillo C. 2 y Andrés Barrera C.3
En este trabajo, se propone el uso de estructuras con tensores como método de implementation de esquemas MIMO, con el objetivo de ampliar los grados de libertad que se tiene al trabajar con matrices, su importancia radica en la flexibilidad que ofrecen los tensores al poder incluir más variables de un sistema para transmitir o recibir información, pero con un costo en complejidad computational. Se verificó que el uso de estructuras con tensores sobre las estructuras MIMO permite obtener los mismos resultados de tasa de error de bit, además de permitir aprovechar un mayor número de grados de libertad en los esquemas de transmisión de múltiples antenas. Finalmente se optimizaron los resultados obtenidos con el esquema tensorial, mediante la teoría de Descomposición de valores singulares (SVD) donde se logró una mejor respuesta gracias a la utilización de los canales con mejores características en cuanto a menor distorsión de la señal y mayor rendimiento del esquema, a expensas de un retraso en la respuesta del sistema y una mayor complejidad computacional.
Palabras clave: MIMO; Tensor; Paradigma; STBC; BER.
In this work the use of tensor structures is proposed as a method of MIMO (Multiple-Input Multiple-Output) schemes implementation, with the target to extend the freedom grades that the matrix array provides, this take importance when include more variables of the system for transmit or receive information a major flexibility is achieved, but with a cost of computational complexity. It was verified that the use of tensor structures in the MIMO schemes allows to obtain the same results of the bit error rate and give the possibility of increase the freedom grades in the transmit structure.
Finally, results obtained with the tensor scheme, using the theory of singular valué decomposition (SVD) which is achieved a better response were optimized through the use of channels with better characteristics in terms of reduced distortion and higher signal yield scheme, at the expense of a delay in the system response and increased computational complexity.
Keywords: MIMO; Tensor; Paradigm; STBC; BER.
El desarrollo y la evolución de las comunicaciones inalámbricas es evidente, día a día se exige mayor rendimiento de los sistemas y calidad de los servicios ofrecidos, de este modo se hace necesario la existencia de tecnologías e infraestructuras que soporten una mayor cantidad de datos y que permita brindar al usuario servicios de forma eficiente y segura (Bravo et al, 2014).
Un esquema basado en la aplicación de tensores tiene como propósito cambiar el paradigma de la estructura MIMO (Multiple Input Multiple Output) la cual se trabaja generalmente en dos dimensiones, con tensores se presenta la oportunidad de incrementar los grados de libertad que se pueden aprovechar en el tratamiento de la información a transmitir, como por ejemplo la utilización de pre-codificación (De Almeida et al, 2008).
Este documento ofrece una reseña básica de la teoría de tensores y los esquemas MIMO incluyendo el modelo del sistema (Izquierdo et al, 2012). Se hace énfasis en la diversidad espacial, para códigos de bloque espacio-temporales (STBC) (Cortes, 2009). Para luego proponer el mapeo de los códigos espacio temporales en la estructura de tensores con el objetivo de conseguir más grados de libertad que se puedan aprovechar en la transmisión de la información. Finalmente, se presentan y analizan los resultados obtenidos y se realizan las conclusiones pertinentes.
Este trabajo está organizado de la siguiente manera. La sección 2 contiene la metodología que proporciona información general sobre la teoría básica de tensores y una breve reseña sobre los esquemas MIMO (Grupalli, 2011), la cual contiene el modelo del sistema en forma matricial donde se encuentra el análisis matemático para los esquemas MIMO de 2x2, 4x4,8x8 y 16x 16 utilizando STBC, y a su vez contiene el modelo tensorial y su optimización propuesta mediante descomposición de valores singulares (SVD) (Demmel, 1997). En la sección 3 se encuentra la simulación y el análisis de los resultados obtenidos en este trabajo. Finalmente, se realizan sus conclusiones.
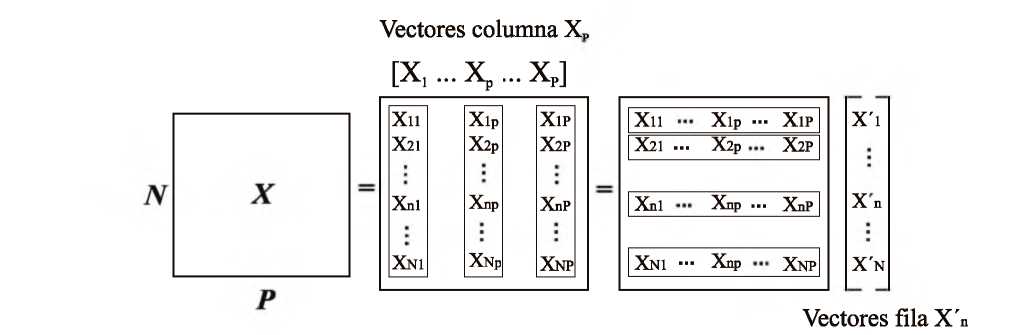
Un tensor puede ser intuitivamente definido como una matriz que representa una señal en múltiples dominios. El orden del tensor es el número de la dimensión, también conocido como las direcciones o modos. Los tensores son generalizaciones de vectores y matrices, por ejemplo, un tensor de tercer orden tiene tres índices (modos o direcciones). Un tensor de orden cero es un escalar, de orden uno un vector, de segundo orden una matriz, y un tensor de tercer orden o mayor se les denomina tensores de alto orden (Izquierdo et al, 2012).
Figura 1. P vectores columna N * 1 o N vectores fila 1 * P (Da Silva, 2009).
El tensor de tercer orden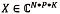 
tiene tres representaciones matriciales X 1 X2,y X3, de la siguiente manera:
Donde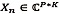 
es el corte n-ésimo considerando el primer dominio fijo, y 
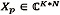es la rebanada p-ésima en el segundo dominio, y 
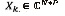es el segmento k-ésimo en el tercer dominio. En este punto, debe quedar claro que X7, X2 y X3 no son tensores, pero si matrices que representan el mismo X
Figura 2. Representación desplegada de un tensor de tercer orden N*P*K (Da Silva, 2009).
Propiedad 1.0 (rango de la suma) Sean X y Y dos matrices con las mismas dimensiones. Entonces rango (X+Y) ≤ rango (X)+rango (Y). Sea y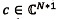 
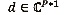otros dos vectores columna de modo que a, b, c y d son linealmente independientes. Definimos 
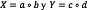,1a anterior propiedad garantiza que X + Y es una matriz de segundo rango.
Figura 3. Suma de factores paralelos (Da Silva,2009).
Esta suma de factores paralelos puede alternativamente expresarse como el producto de dos matrices A y BT se define como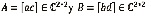 
Como se aprecia en la Figura 4, donde cada matriz tiene dos factores paralelos (Da Silva, 2009).
Figura 4. Representación gráfica de la suma de factores paralelos (Da Silva, 2009).
La suma de las dos matrices del mismo rango puede ser factorizada como el producto de dos matrices. Este resultado puede generalizarse a la suma R de un rango de matrices en la forma X (r) = a(r) ° b(r) de tal manera que:
MIMO es un mecanismo que incrementa la eficiencia espectral de un sistema de transmisión inalámbrica por medio de la utilización del dominio espacial, aprovechando fenómenos físicos como la propagación multitrayecto para incrementar la velocidad de transmisión o reducir la tasa de error de bit. MIMO se basa en el dominio espacial, por lo tanto requiere el uso de múltiples antenas en el transmisor y en el receptor.
MIMO se basa en la utilización del dominio espacial, creando "canales espaciales" diferenciados entre el transmisor y el receptor. Para ello es necesario emplear múltiples antenas tanto en el transmisor como en el receptor. Estas antenas deben estar separadas por una distancia mínima que permita la creación de estos canales espaciales diferenciados.
En el caso específico de MIMO, se toma en cuenta la diversidad espacial con el propósito de generar múltiples caminos haciendo uso de múltiples antenas en el transmisor y en el receptor. Para llegar a este punto la tecnología ha evolucionado de la siguiente forma (Grupalli, 2011):
Figura 5. Esquemas SISO, MISO y SIMO, respectivamente.
Como se hace evidente, MIMO representa el sistema que utiliza dos o más antenas en el transmisor y dos o más antenas en el receptor, es decir utiliza diversidad espacial a través del uso de múltiples antenas.
Figura 6. Esquema MIMO
Los sistemas MIMO se componen de tres elementos principales, el transmisor (TX), el canal (H), y el receptor (RX). Donde Nt denota el número de antenas en el transmisor, y Nr denota el número de antenas en el receptor. La Figura 7 representa el diagrama de bloques del sistema MIMO (Cortes, 2009).
Figura 7. Diagrama en bloques del sistema MIMO (Cortes, 2009).
El canal con Nr salidas y Nt entradas se denota como una matriz Nr*Nt.
Donde cada entrada hi,j denota la atenuación y cambio de fase (función de transferencia) entre el jth transmisor y el ith receptor. Se supone en ese documento que el canal MIMO se comporta de una manera "cuasi-estática", es decir, el canal varía aleatoriamente de ráfaga a ráfaga, pero es fijo dentro de una transmisión (Vucetic et al, 2003).
El modelo de señal MIMO se describe como
Donde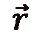 
es el vector recibido de tamaño Nr* 1, H es la matriz de canales de tamaño Nr * Nt 
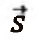es el vector de transmisión de tamaño Nt* 1 , 
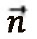es el vector de ruido de tamaño Nr * 1. Cada elemento de ruido se modela normalmente como ruido blanco gaussiano distribuido idénticamente independiente (i.i.d.), con una varianza Nt/2 *SNR (Vucetic et al, 2003).
Para el caso de 4 antenas de transmisión (Nt= 4), se proporcionan códigos de bloque de tasa 1/2, con plena diversidad 4Nr. El código de bloque es el siguiente (Cortes, 2009):
Con una tasa de 1/2 ya que 4 símbolos se transmiten en 8 intervalos de tiempo. Para decodificar, el decodificador ML (Maximum Likelihood) minimiza la decisión métrica de las ecuaciones para la decodificación de s 1, s2, s3, y s4 (Cortes, 2009). Dónde ξ para Nt = 4, está dada por:
Y,
Para el caso de 8 antenas de transmisión (Nt= 8), se proporcionan códigos de bloque de tasa 1/2, con plena diversidad 8Nr. El código de bloque es el siguiente:
Con una tasa de 1/2, ya que 8 símbolos se transmiten en 16 intervalos de tiempo. Para decodificar, el decodificador ML minimiza la decisión métrica de las ecuaciones para la decodificación de S1S2,S3,S4,Ss,S6,S7 y S8. De igual forma, para el caso de 16 antenas de transmisión (Nt = 16), se proporcionan códigos de bloque de tasa 1/2, con plena diversidad 16 Nr. Siguiendo la misma metodología de los esquemas anteriores.
En la Figura 8. Se puede apreciar el diagrama de bloques del sistema propuesto. Cuenta con Nt antenas transmisoras y Nr antenas receptoras, donde Nt = Nr para todos los casos que serán estudiados, se utilizarán sistemas MIMO de diversidad para la transmisión. En el transmisor, la secuencia de entrada en serie se convierte en R flujos de datos paralelos que se extienden a través de un subconjunto de Nt antenas de transmisión y durante P intervalos de tiempo. Se trabaja bajo el caso l≤R≤Nt para garantizar que por lo menos un canal se encuentra en buenas condiciones de transmisión. Cada flujo de datos transmitidos es una colección de N símbolos durante el cual se supone que el canal inalámbrico va a ser constante. La atenuación del canal es constante, plana en función de la frecuencia. Se supone que la potencia de transmisión por corriente de datos es fija. Se considera una transmisión de lazo abierto ya que el esquema no cuenta con la capacidad de corrección de errores ni selección de antena, ya que la investigación busca medir el rendimiento del esquema cambiando el paradigma a una visión tensorial.
Se supone un conocimiento perfecto del canal tanto en el transmisor como en el receptor y por lo tanto estos poseen los algoritmos necesarios para la codificación y la decodificación. Se supone que las antenas están separadas adecuadamente y que el medio de propagación es lo suficientemente rico en dispersión de modo que puede ser modelado como una variable aleatoria Gaussiana compleja con media cero y varianza igual a la unidad.
Figura 8. Diagrama de bloques del modelo tensorial propuesto
Sea hNtNr el canal espacial entre la antena de transmisión Nt-ésimo y la Nr-ésima antena de recepción, Sn,r sea el símbolo N-ésimo de la secuencia de datos, r-ésimo después de la conversión de serie a paralelo, y Ap,Nt ser el p-ésimo elemento del Mf-ésimo código. Se define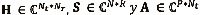 
como las matrices de canal, símbolos y código, donde hNt=[H]Nt, Nr Sn,r=[S]n,r Ap,N,t = [A]p,Nt son, respectivamente, los elementos típicos de estas matrices. Se puede ver la versión de banda base de tiempo discreto de la señal recibida en el Nrth antena receptora, n-th período de símbolos y p-th intervalos de tiempo como un tensor de tercer orden 
.
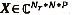El tensor estará conformado por la concatenación de tres bloques, como se aprecia en la Figura 9, el primer bloque será la matriz de símbolos conformada por el flujo de datos a transmitir, el segundo bloque corresponderá al canal de frecuencia plana de dimensiones Nt * Nr y finalmente, el tercer bloque será la redundancia aplicada a los N símbolos a transmitir siguiendo el algoritmo de código de bloque espacio -tiempo.
Figura 9. Diagrama de bloques del tensor - Señal
Se puede organizar la información contenida en X de tres maneras diferentes. Se define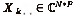 
como una matriz-slice del tensor que recoge P * N muestras de la señal recibida en P intervalos de tiempo y los períodos de símbolo N en la Nr -ésima antena de recepción. Del mismo modo, se puede definir, alternativamente, la slice 
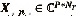recoge las muestras de las señales recibidas en P intervalos de tiempo y Nr antenas receptoras asociadas con el símbolo enésimo, y la slice 
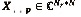que recoge Nr*N muestras de la señal recibida de la antenas de recepción y N símbolos para los P ranuras de tiempo de tiempo. La factorización de 
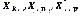como una función de los parámetros del sistema que son dados, respectivamente, por las siguientes expresiones:
Para la simulación del sistema se utilizó el software Matlab, los símbolos a transmitir se generaron aleatoriamente, se trabajó con 900.000 símbolos por cada valor de SNR ya que una imagen HD (High Definition) posee 0,9 Mega-pixeles ya que el objetivo de los sistemas de comunicaciones de hoy en día es transmitir servicios de calidad a sus usuarios, el sistema realiza 10.000 iteraciones por cada valor de SNR como lo estipula el método de Montecarlo. La configuración de canal inalámbrico se consideró con una distribución de Rayleigh con el uso de la atenuación del canal constante, plana en función de la frecuencia y con adición de ruido blanco gaussiano. Se implementaron los esquemas MIMO G2, G4 Gg y G1 de forma matricial y tensorial para comprobar el cambio de paradigma al igual de los esquemas G2, G4 y G8 optimizados a través de descomposición en valores singulares (SVD). La modulación usada fue 16-QAM aspecto que se destaca en esta investigación ya que todas las investigaciones realizadas anteriormente acerca del tema solo trabajan modulación BPSK y QPSK.
Sea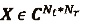 
una matriz de valores complejos de rango R. Entonces, la descomposición en valores singulares (SVD) de X está dada por:
Donde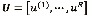 
es una matriz unitaria
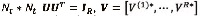es una matriz unitaria
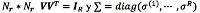es una matriz diagonal RxR.
SVD descompone una matriz X rango R en una suma de R matrices de rango uno, donde X es una matriz cuadrada. Cada uno de estas matrices de rango uno representa un elemento de base del subespacio generado por la matriz X, que se pondera por los valores singulares σ(1),•••, σ(2)(Demmel, 1997).
En el caso específico de esta investigación, para realizar la optimización de los esquemas tensoriales que representan estructuras MIMO de 2x2,4x4 y 8x8, mediante el método de descomposición de valores singulares (SVD), se eligió el máximo valor contenido en cada columna de la matriz de canal ya que el hecho de tener un mayor valor singular garantiza un mejor rendimiento en el esquema, debido a que se hará uso de los subcanales con las mejores características en cuanto a la distorsión que adiciona a las señales (Da Silva, 2009). Los valores singulares obtenidos se reorganizan en una matriz diagonal y se multiplican por la matriz de símbolos a transmitir como lo muestra la Figura 10.
Figura 10. Matriz a transmitir con SVD
Para garantizar que todos los símbolos de la matriz sean transmitidos se necesita igual número de iteraciones como antenas de transmisión presentes en el esquema, así un esquema de Nt *Nr donde Nt=Nr requiere Nt iteraciones para transmitir la totalidad de datos contenidos en la matriz, ya que el número de subcanales es igual al número de antenas transmisoras (Nt) en todos los casos, lo que genera un retraso de (Nt-l) iteraciones con respecto al esquema que hace uso de todos los subcanales de la matriz de canal, pero a cambio de esto se obtiene un mejor rendimiento de la BER en la relación a la SNR.
Para la verificación de los esquemas MIMO, se implementó de la manera convencional (esto es, por matrices), y mediante el esquema tensorial propuesto para sistemas de 2x2, 4x4, 8x8 y 16x16, obteniendo los siguientes resultados.
Figura 11. Esquema MIMO G2 Matricial y Tensorial
Figura 12. Esquema MIMO G4 Matricial y Tensorial
Figura 13. Esquema MIMO G8 Matricial y Tensorial
Figura 14. Esquema MIMO G16 Matricial y Tensorial
Al comparar los dos resultados en todas las simulaciones se puede verificar que el rendimiento del sistema es aproximadamente el mismo con relación al esquema MIMO convencional como era de esperarse, pues el objetivo era conseguir mapearlos en estructuras con tensores que permitan ampliar la expectativa de poder manejar mayor número de grados de libertad, esto para buscar mecanismos o estrategias que optimicen la transmisión de cualquier tipo de servicio de comunicaciones. Verificado en Cortes (2009) y Wu et al (2007). Los esquemas presentan ganancia de diversidad espacial, en los cuales se consigue una tasa de error muy por debajo de los límites que pueden ser requeridos para la prestación de un servicio de comunicación. Esto se debe a que la ganancia de diversidad se da por la redundancia de la información introducida en el esquema de transmisión. En cuanto a la relación señal a ruido el resultado es alto en el esquema de 2x2 y va disminuyendo progresivamente hasta el de 8x8, en la gráfica de 16x16 se observa un rendimiento inesperado o que no sigue la lógica que se venía trabajando pues la tasa de error de bit no desciende paulatinamente con el incremento de la relación señal a ruido, sino que lo hace de forma muy lenta y a la altura de una SNR de 5 dB el resultado obtenido escasamente alcanza un valor próximo a 1*10 ", esto se debe a que el aumento del tamaño de la matriz aun cuando se trabaja con datos de coma flotante de 16 bits no proporciona la suficiente precisión al momento de realizar las operaciones, lo que ocasiona saturación en la simulación, para minimizar este problema se puede trabajar con datos de coma flotante de 32 bits en un simulador de mayor robustez y precisión. Verificado enWu et al (2007).
En este caso se realizaron simulaciones teniendo en cuenta la optimización con SVD propuesta para los esquemas de 2x2,4x4 y 8x8, debido a que el resultado de 16x16 no es óptimo, ya que no sigue el comportamiento lógico y esperado. Obteniendo los siguientes resultados.
Figura 15.Comparación de Esquema MIMO tensorial G2 con y sin optimización
Figura 16.Comparación de Esquema MIMO tensorial G4 con y sin optimización
Figura 17.Comparación de Esquema MIMO tensorial G8 con y sin optimización
Para el caso de G16, ya que no sigue el comportamiento lógico y esperado en comparación con los demás esquemas y presenta algunas fallas de saturación del software en el que fue implementado, no se realizó optimización y se propone como objetivo para futuras investigaciones.
En todas las simulaciones se puede observar que con la adición de la teoría de SVD los esquemas mejoraron su rendimiento, para el caso de G2 se redujo en un 12% la SNR (Línea magenta) comparado con el esquema tensorial propuesto inicialmente (Línea morada), para el caso de G„ se mejoró su rendimiento reduciendo en un 26% la SNR (Línea azul) comparado con el esquema tensorial propuesto inicialmente (Línea cian), y para el caso de G8 se redujo en un 60% la SNR (Línea roja) comparado con el esquema tensorial propuesto inicialmente (Línea verde), de esta forma se observa que el aumento en el número de antenas transmisoras y receptoras incrementó el porcentaje de optimización de los esquemas lo que hace que los servicios de comunicaciones puedan ser brindados a los usuarios con mayor calidad y menor requerimiento de potencia, a cambio de más espacio físico e infraestructura en las aplicaciones reales de los esquemas.
Se planteó una estructura tensorial que permite ampliar los grados de libertad en comparación con la estructura de matriz con la que se han venido implementando los esquemas MIMO. El esquema tensorial propuesto es una concatenación de matrices, en este caso, la matriz de símbolo S, la matriz de canal H y la matriz de codificación A. Los símbolos son agrupaciones de 4 bits debido a que la modulación utilizada es 16-QAM, se usan 900.000 símbolos debido a que una imagen HD posee 0.9 Megapíxeles. Realizando la comparación de la tasa de error de bit entre los esquemas MIMO convencionales de 2x2, 4x4, 8x8 y 1£x1£ siguiendo el modelo de códigos de bloque espacio-tiempo y la estructura con tensores propuesta, la atenuación del canal es constante, plana en función de la frecuencia, se consiguen resultados de la tasa de error de bit aproximados (de una matriz o tensor rango dos a un tensor de alto orden rango tres). Además, se hace evidente que un incremento en el tamaño del esquema que se traduce en un aumento de antenas transmisoras y receptoras permite obtener un mejor rendimiento (excepto en el esquema MIMO 1£x1£), lo que equivale a una determinada tasa de error de bit disminuyendo la relación señal a ruido del sistema.
Luego, se optimizó el esquema MIMO mediante la utilización de la teoría de Descomposición de Valores Singulares (SVD), para obtener un mejor rendimiento en los sistemas gracias a la visión del tensor y la posibilidad de adicionar otras variables de estudio. En este caso SVD se usó como medio para conocer los subcanales más eficientes de los esquemas y mediante la reorganización de la matriz de canal, usar un conjunto de subcanales que permitieran disminuir el error y la potencia necesaria en la transmisión y recepción de los símbolos. Esta optimización se realiza a expensas de un retraso de (M-l iteraciones), debido a que los canales óptimos para enviar la información se reducen a (l/Nt canales) del tamaño real de la matriz de canal inicial, al igual que un aumento en la complejidad computational de los sistemas ya que se incrementa la cantidad de operaciones necesarias para realizar el proceso de transmisión/recepción de los datos.
1. Albentia System (S. F). WHITE PAPER: Tecnología MIMO. Madrid - España.
2. Bravo, M; Trujillo Cabrera, D & Barrera Canchón, A. (2014). Propuesta de estructuras con tensores para la implementación de esquemas MIMO. Colombia
3. Cortés-Peña, L.M. (2009). MIMO Space-Time Block Coding (STBC): Simulations and Results [Design Project: Personal and Mobile Communications, Georgia Tech (ECE££04)].
4. Da Silva, I.L.J. (2009). Multi-user receiver processing for inter-cell interference reduction in pucch LTE [tesis de maestría]. Universidad Federal Do Ceará: Fortaleza-Brazil.
5. De Almeida, A.L.F., Da Silva, I.L.J., Favier, G., & Cavalcanti, F.R.P. (2008). Tensor-based precoding with blind MIMO channel estimation and transmit antenna selection. IEEE 9th Workshop on Signal Processing Advances in Wireless Communications, 2008. SPAWC 2008, (pp.38£-390). Piscataway, NJ: IEEE
6. Fernández Fernández, O. (2007). Caracterización Experimental y Modelado de Canal MIMO para aplicaciones WLAN y WMAN. Universidad de Cantabria - Santander
7. Grupalli, S.A., Cabrera, M.A., Bilbao, J. D., & Ferreyra, M.G. (2011). Sistemas de comunicación inalámbricos con tecnología MIMO. CET, (34), 7-13
8. Izquierdo, J. & Crespo, C. (2012). Caracterización de canal no lineal usando modelos de Volterra-Parafac. Sevilla, España: Universidad de Sevilla
9. Oestges, C. & Clerckx, B. (2007). MIMO Wireless Communications: From real-world propagation to space-time code design. Elsevier Ltd. (California USA)
10. Roemer, F., et al. (2011). Tensor-based semi-blind channel estimation for MIMO OSTBC-coded systems. En 2011 Conference Record of the Forty Fifth Asilomar Conference on Signáis, Systems and Computers (ASILOMAR). (pp. 449-453). Piscataway, NJ: IEEE
11. Sorensen, M. & De Lathauwer, L. (2012). Tensor decompositions with vandermonde factor and applications in signal processing. 2012 Conference Record of the Forty Sixth Asilomar Conference on Signáis, Systems and Computers (ASILOMAR), (pp.890-894). Piscataway, NJ: IEEE
12. Vucetic, B y Yuan, J (2003). Space-Time Coding. Chichester, UK: John Wiley & Sons
13. Wallace, J.W. & Maharaj B .T. (2007). The accuracy of tensor and directional methods for MIMO channel modeling. En EuCAP 2007. The Second European Conference on Antennas and Propagation, 2007. Hertfordshire, Uk: IET
14. Weichselberget, W. (2004). On the decomposition of the MIMO, channel correlation tensor. En ITG Workshop on Smart Antennas 2004, (pp.2£8-273). Piscataway, NJ: IEEE.
15. Wu, D; Eilert, J; Lui, D. (2007). Fast Complex Valued Matrix Inversión for Multi-User STBC-MIMO Decoding. Estados Unidos.
