Artículo
Revista Ingeniería y Región 2014 (12): 105-127

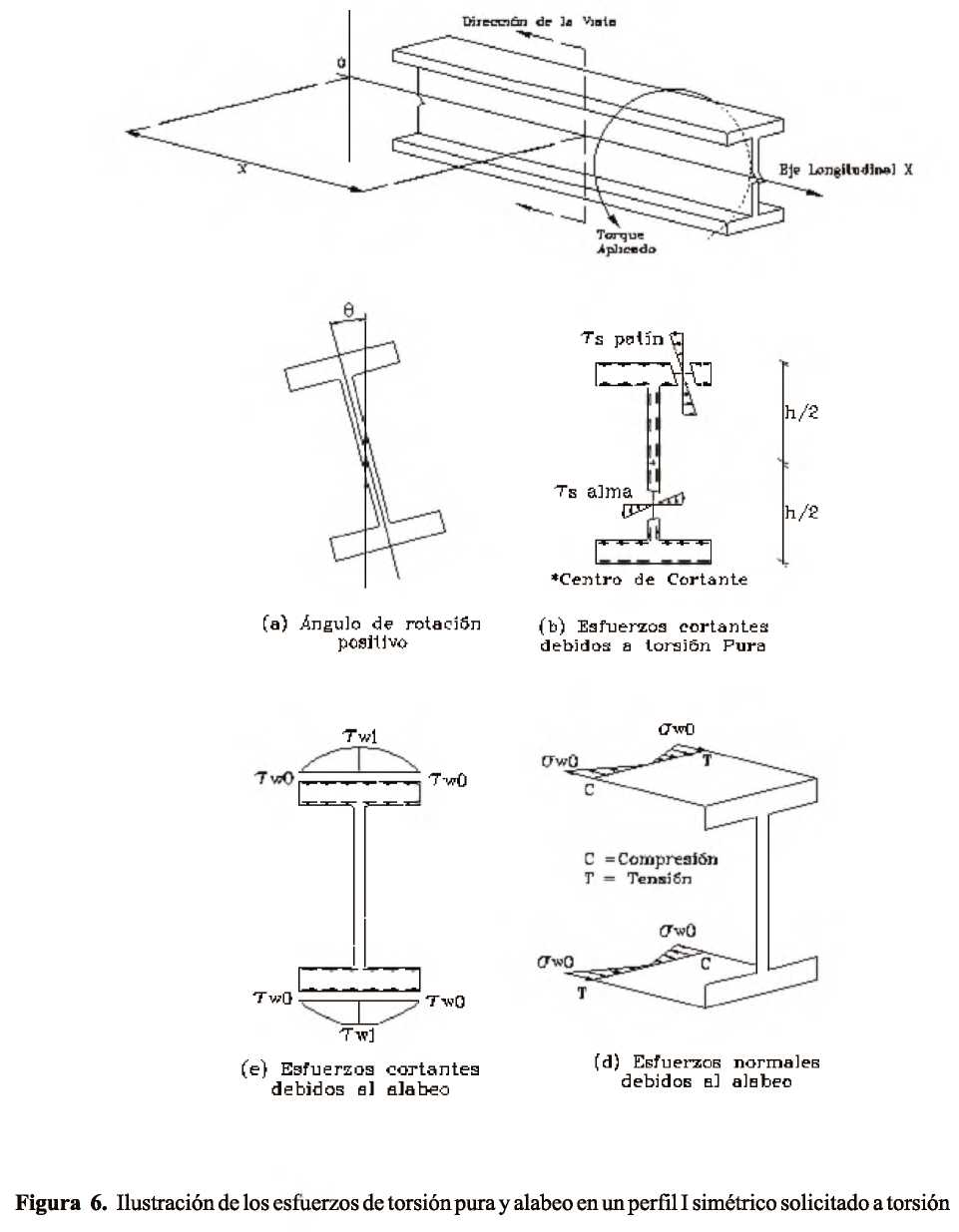
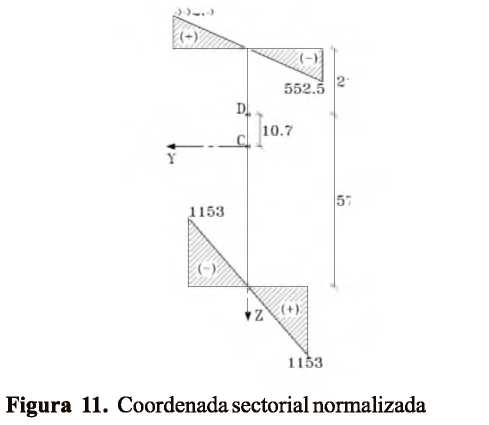
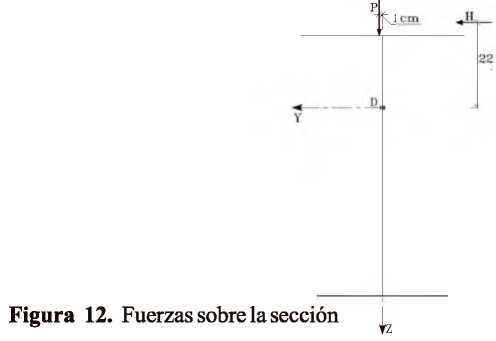
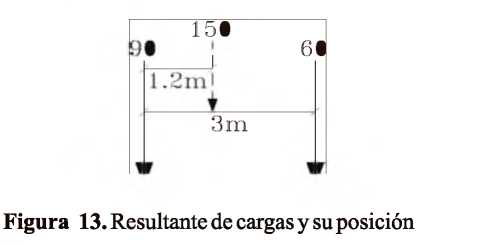
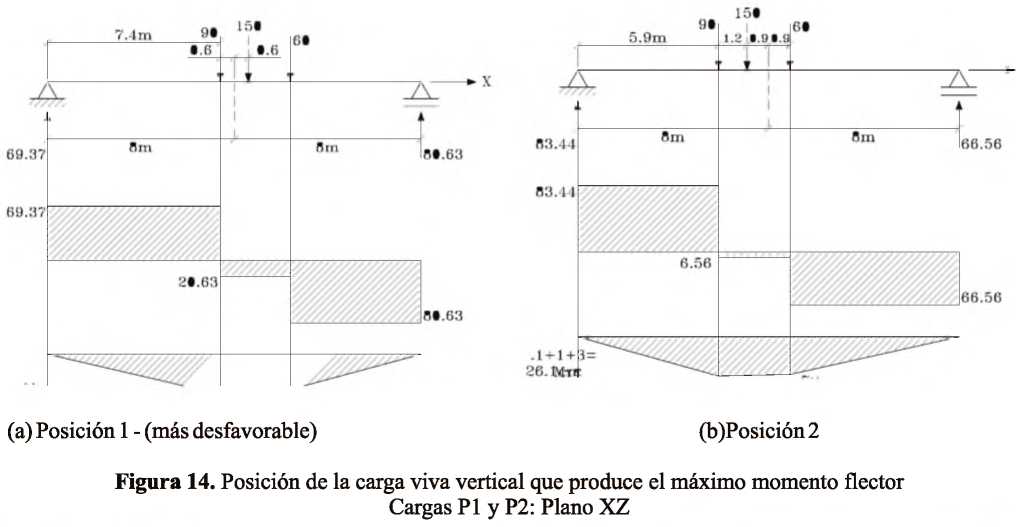
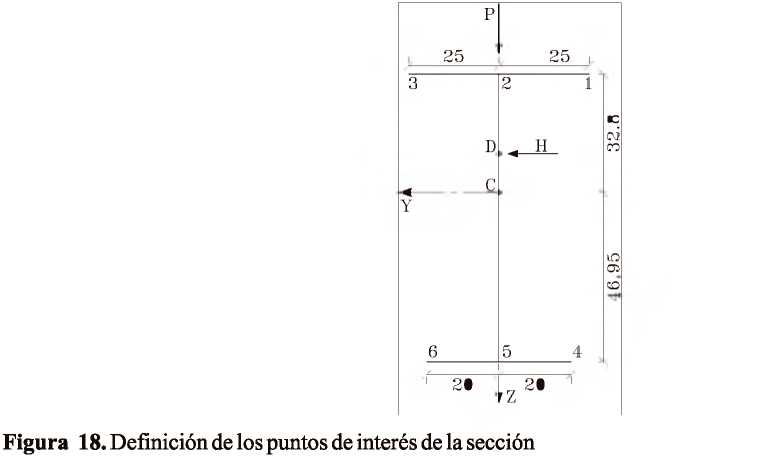
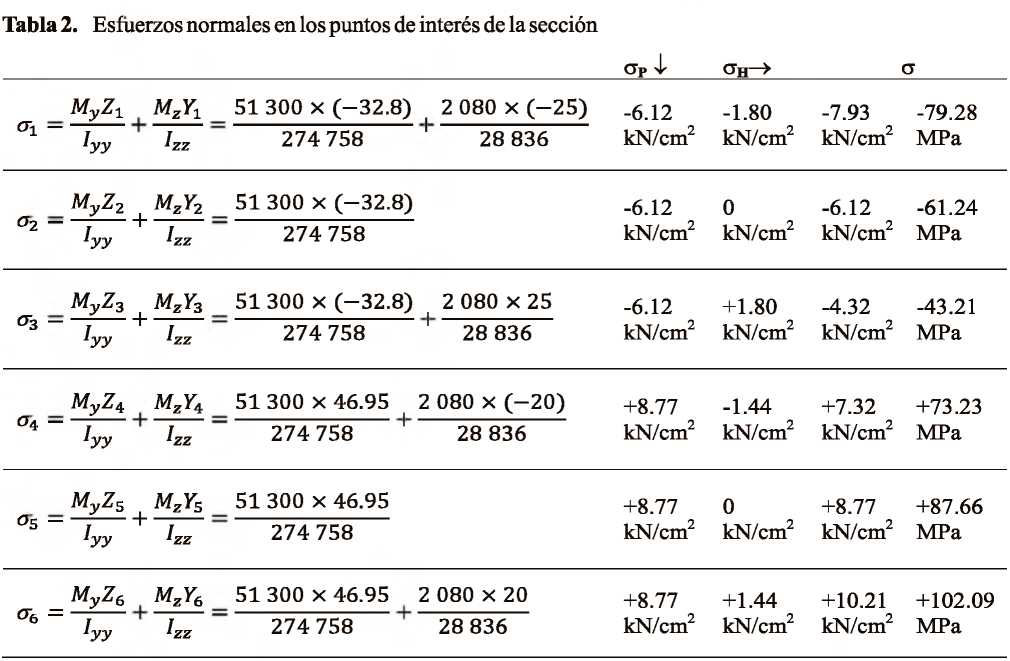
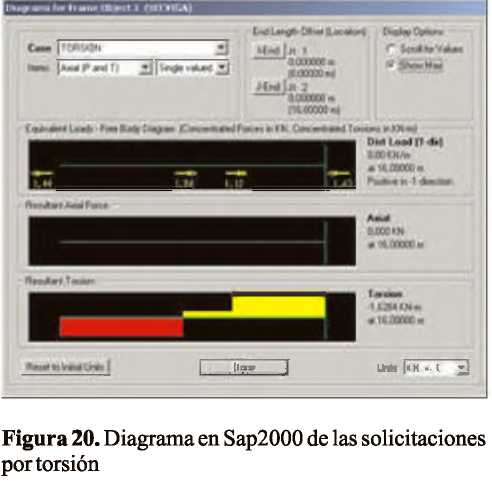
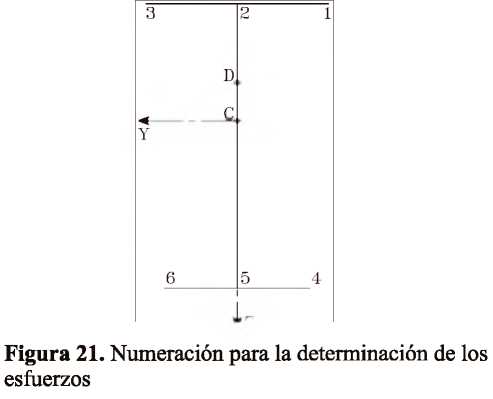
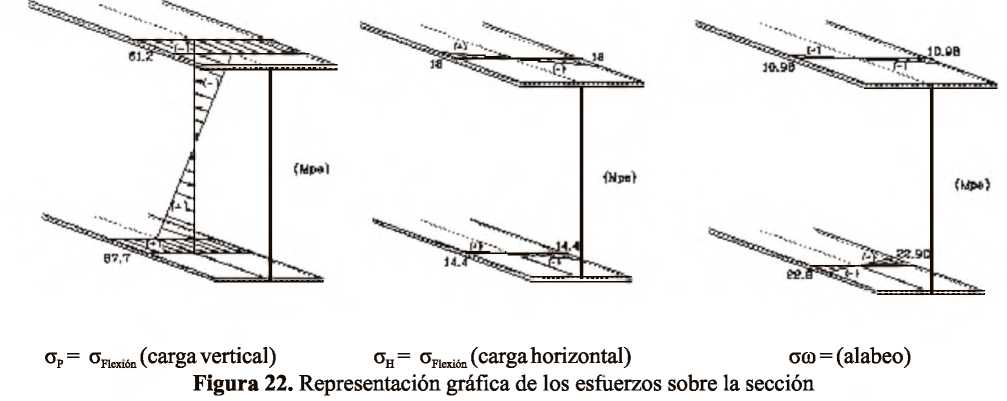
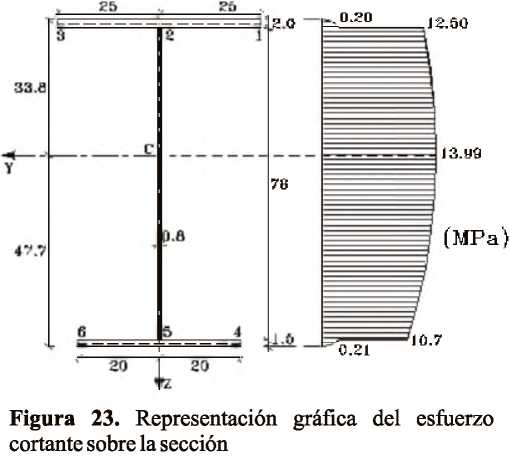
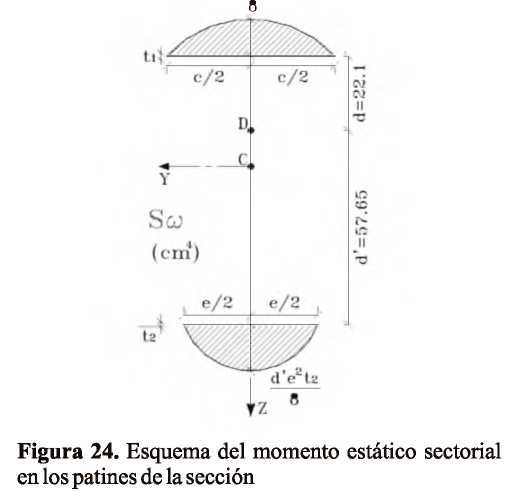
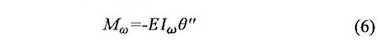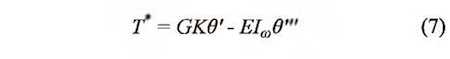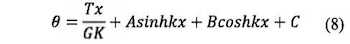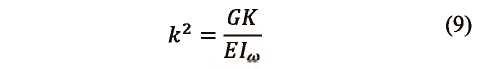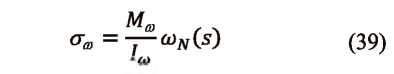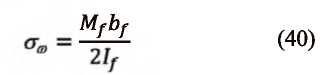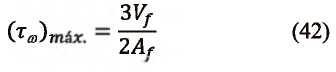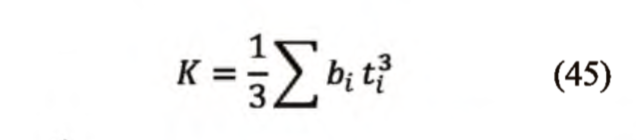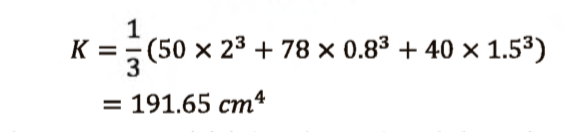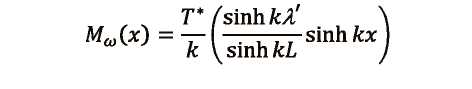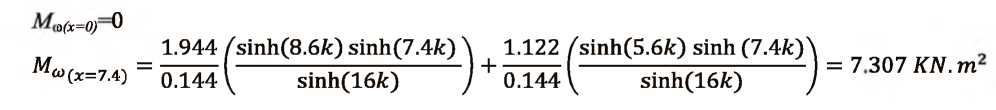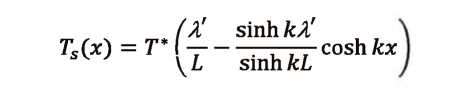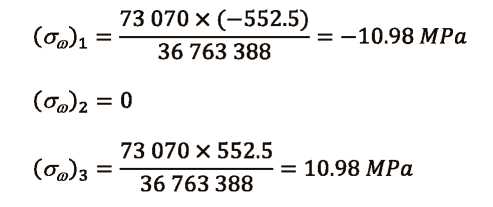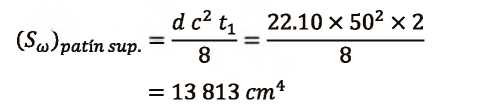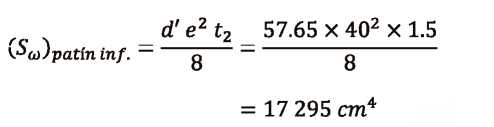Determinación de los esfuerzos producidos por flexo-torsión
Caso de estudio: Análisis de las vigas metálicas de un puente grúa

Efforts in beams subjected to torsion and bending
Case: Analysis of steel beam bridge-crane

Carlos R. Vallecilla Bahena1, Myriam R. Pallares Muñoz2 y Julián A. Pulecio Díaz3

1Magíster en Ingeniería Civil. Universidad Nacional de Colombia. Investigador Grupo de Investigación INDETEC-Universidad de la Salle.-Colombia. E-mail: vallecillacarlos@yahoo.com
2Magíster en Métodos Numéricos para Cálculo y Diseño en Ingeniería. Universidad Surcolombiana. Avenida Pastrana Borrero Carrera 1, Neiva-Colombia. E-mail:myriam.pallares@usco.edu.do
3Magíster en Construcción de Obras. Universidad Cooperativa. Calle lONo. 1-120 Ed. Urrutia, Ibagué-Colombia. E-mail: julpul7@hotmail.com

Recibido: 30 de Mayo de 2014
Aprobado: 9 de Agosto de 2014

Resumen:

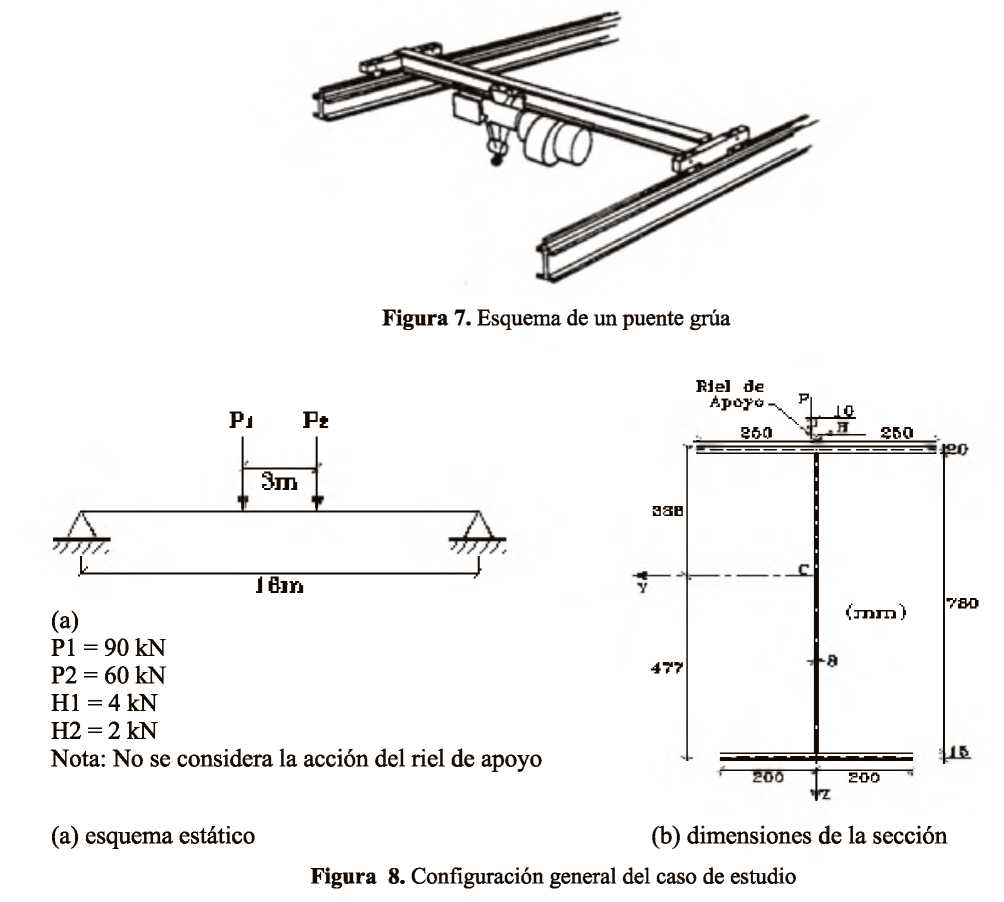
En toda estructura se originan esfuerzos debidos a torsión cuando la resultante de las fuerzas no pasa a través del centro de cortante de la sección. A su vez el centro de cortante tiene una doble significación: por una parte es el punto donde debe aplicarse la resultante de cargas para que una estructura se desplace sin rotar y por otra, es el punto con respecto al cual una estructura gira cuando es sometida a momentos torsionales. Normalmente, ocurren solicitaciones debidas a la torsión de Saint Venant y a la torsión de alabeo. La diferencia fundamental entre ellas, radica en la forma como se distorsiona la sección. Mientras las primeras, se caracterizan por la presencia de esfuerzos cortantes en el plano de la sección, en las segundas aparecen además, desplazamientos en el sentido longitudinal de la estructura, que se traducen en la presencia de esfuerzos normales. Para ilustrar las características de la torsión de alabeo se reporta en el presente artículo un caso de diseño de un puente grúa en estructura metálica, que se encuentra sometido a la acción de un tren de cargas móviles. Con esta elección, se desea mostrar la aplicación de la teoría de las áreas sectoriales en la determinación de los esfuerzos debidos a la torsión de alabeo en una construcción de la práctica diaria de un ingeniero diseñador de estructuras.

Palabras clave: torsión; teoría de áreas sectoriales; alabeo; centro de cortante; momento de inercia sectorial; funciones torsionales; esfuerzos cortantes debidos a la torsión de alabeo.

Abstract:

In all structures stresses due to torsion are originated when the resultant of the forces doesn't cross by the shear center of the section. Shear center as well has one double meaning: on the one hand it's the point where the resultant of loads must be applied so that a structure moves without rotating and by another one, is the point with respect to which one structures rotate, when it's put under torsional moments. Normally, solicitations due to the Saint Venant Torsion and the Warping Torsion, occurring. The fundamental difference among them is in the form as the section is distorted. While first, they are characterized by the presence of the shear stresses in the plane of the section, in second appear in addition, displacements in the longitudinal direction that are translated in the presence of normal stresses. In order to illustrate the characteristics of the Warping Torsion a case of design of a bridge crane in metallic structure is reported in the present article, that is put under the action of a train of live loads. With this election, it's desired to show the application of the theory of the sectorial areas in the determination of the stresses due to the Warping Torsion in a construction of the daily practice of an engineer designer of structures.

Keywords: torsion; sectorial area; warping torsion; shear center; sectorial moment; torsional functions and shear stresses due to warping torsion.

1. Introducción

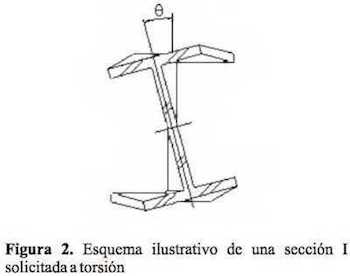
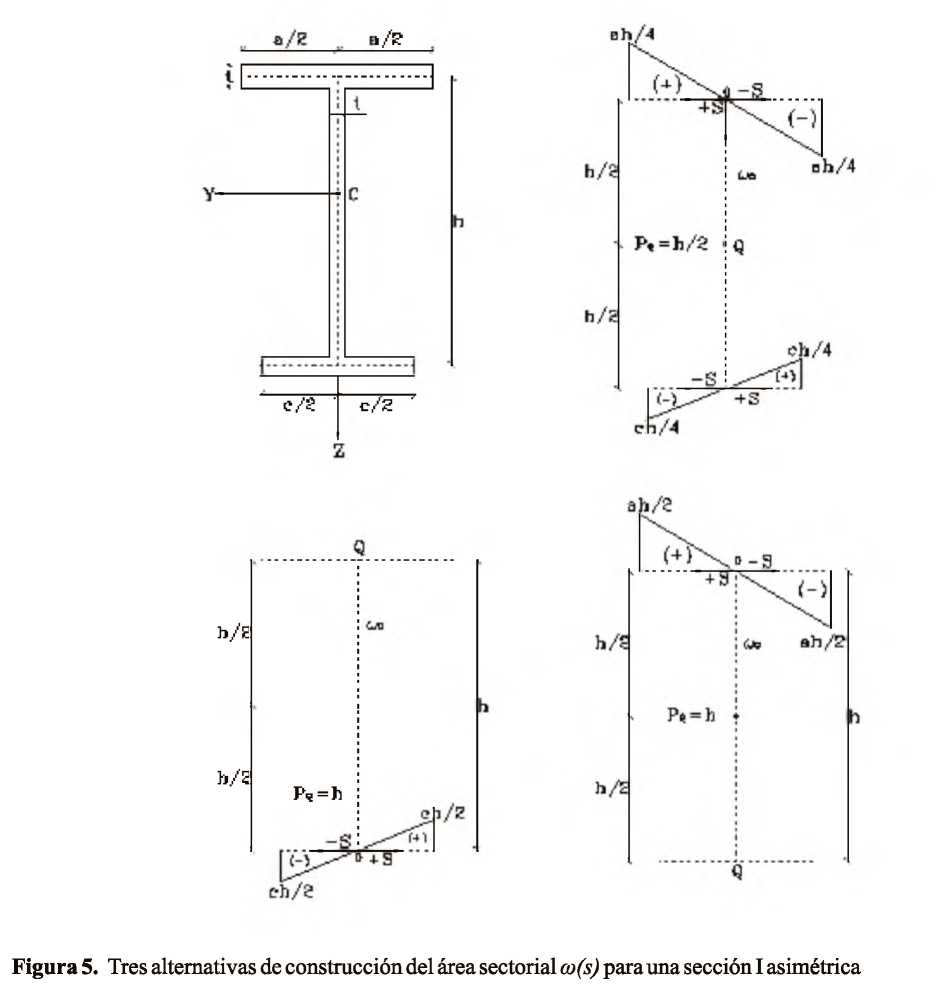
El desconocimiento que en ocasiones existe en el medio ingenieril, de los esfuerzos causados por la torsión, indica la necesidad de llevar a cabo un estudio detallado de estas solicitaciones, sus características y efectos sobre las construcciones. Las secciones de pared delgada, tales como perfiles metálicos, muros de cortante en edificios y puentes de sección abierta y cerrada, demandan un estudio cuidadoso de las solicitaciones generadas por la torsión (Vallecilla, 2005). En particular, interesan los esfuerzos producidos por el alabeo de la sección, es decir, por el desplazamiento de los puntos de esta a lo largo de su eje longitudinal. Si el desplazamiento se encuentra impedido, se generan, además de los esfuerzos cortantes, esfuerzos normales a lo largo de la sección, cuya obtención es esencial para la seguridad de la construcción (Monleón, 1999). Este trabajo trata la torsión de Saint Venant y la de alabeo, la determinación de las propiedades torsionales de una sección típica en ingeniería (perfil I asimétrico) y la obtención de la posición del centro de cortante, entre otros, reportados a través de un caso típico de estudio. Una discusión completa de la teoría torsional está más allá del alcance de esta publicación, no obstante, en los siguientes apartados se presenta una breve discusión para describir el método de análisis usado.

Una cobertura más detallada de la teoría torsional y de otros asuntos, está disponible en las referencias dadas.

2. Métodos

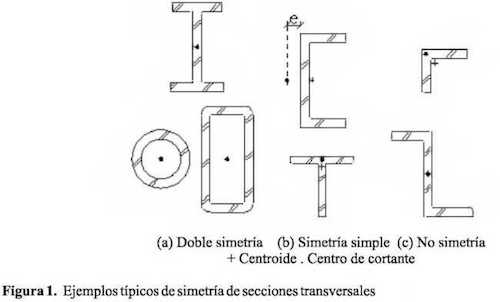
La torsión es la rotación de un miembro alrededor de su eje longitudinal y ocurre cuando la resultante de las fuerzas aplicadas no atraviesa el centro de cortante de la sección (Vlassov, 1948). Por su parte, el centro de cortante es el punto por el que deberían pasar las cargas aplicadas para que produzcan flexión sin originar torsión. Si una sección tiene un eje de simetría, el centro de cortante siempre está sobre dicho eje; para secciones transversales con dos ejes de simetría, dicho centro se encuentra en la intersección de estos (al igual que el centroide) (Ortiz, 2002). De acuerdo a los ejemplos ilustrados en la figura 1 a, el centroide y el centro de cortante coinciden en secciones doblemente simétricas. Las secciones con un solo eje de simetría tienen su centro de cortante sobre este eje, pero no necesariamente en el centroide. En la figura 1 b, se señala el centro de cortante para secciones tipo canal. En ellas, el centro de cortante se encuentra ubicado a una distancia e de la cara del canal. Por su parte, el centro de cortante de una sección tipo T está en la intersección de las líneas centrales del ala y el alma. La localización del centro de cortante para las secciones asimétricas tales como ángulos (L) y formas tipo Z se muestran en la figura 1 c.

Si en cualquiera de las secciones ilustradas en la figura 1 se aplica una fuerza en cualquier punto fuera del centro de cortante, se configurará un caso típico de flexo-torsión (Timoshenko, 1977). En general, el desempeño a torsión de secciones transversales cerradas es superior al de secciones abiertas. Las formas cerradas circulares, son las más eficientes para resistir la carga de torsión. Otras formas cerradas como cuadrados y rectángulos, también proporcionan una resistencia considerablemente mejor a la torsión que las formas abiertas (p. ej. perfiles I y canales). Cuando deben utilizarse formas abiertas, su resistencia torsional se puede aumentar creando un cajón.

2.1 Resistencia de la sección transversal a un momento torsional

En cualquier punto de la longitud de un miembro sujeto a un momento torsional, la sección transversal rotará con un ángulo 6 como se indica en la figura 2. En las secciones transversales que son no-circulares esta rotación está acompañada de alabeo, es decir, las secciones no permanecen planas (Hartog, 1980). Se define entonces el alabeo, como el desplazamiento ¡pt, normal al plano de la sección (en la dirección del eje longitudinal del miembro solicitado a torsión).

En la figura 2, d es el ángulo de torsión. La rotación de un miembro se mide por medio de este parámetro que indica cuánto rota la sección en un punto x del miembro (x es la dirección longitudinal) con respecto a un origen previamente establecido. El ángulo de torsión depende del origen (x=0). Si el alabeo es totalmente libre (p. ej. secciones circulares compactas y huecas) o casi libre (p. ej. secciones L y T), el momento torsional resistido por la sección transversal es:

Esta torsión se denomina torsión uniforme de Saint Venant y supone que la sección puede alabearse de forma libre, por lo que los esfuerzos producidos son sólo de corte (r) y no normales (aj. Este tipo de torsión predomina en las secciones compactas y huecas continuas. En estas, las solicitaciones por torsión son absorbidas por un flujo de cortante continuo en toda la sección. Los miembros con libre alabeo absorben las solicitaciones por torsión por medio de los esfuerzos de corte sin esfuerzos normales (Kollbrunner & Basler, 1970).

En la ecuación (1):

Nótese que 9' es una función del momento torsor aplicado, en cada sección

El término (GK) se conoce como rigidez torsional de Saint Venant y la constante de torsión (K), para cualquier sección se calcula como:

En la ecuación (2):

A = Área de la sección transversal [L2]

Ip= Momento polar de inercia de la sección [L4]

Cuando la tendencia a que una sección transversal se alabee libremente se impide, resulta flexión longitudinal. Esta flexión viene acompañada de esfuerzos de corte en el plano de la sección transversal que resisten el momento torsional aplicado (Reismann, 1980). Esta torsión, se denomina torsión de alabeo (torsión no uniforme) y supone que la sección del miembro solicitado a torsión no puede alabearse de forma libre resultando de esta manera, tanto esfuerzos cortantes (ra) como normales (o-*) (Kollbrunner & Basler, 1970). Este caso se presenta cuando, por ejemplo, uno de los extremos de la barra está empotrado.

Está demostrado que la torsión de alabeo cumple la siguiente relación:

Donde:

TtÜ = Momento resistente debido al alabeo restringido de la sección transversal, ó, torsión de alabeo [F-L]

E = Módulo de elasticidad [F-L"2]

4 = Momento sectorial de inercia, ó constante de torsión de alabeo [L6]

EIm = Característica de la sección [F-L4]

9'" = Tercera derivada de respecto a x[L ’]

En un perfil I solicitado a torsión como el de la figura 2, la deformación por alabeo, ocurre por efecto de las fuerzas de corte (Vy) que se generan en los patines. El momento torsional de alabeo (Tm), es el momento torsional absorbido por los patines, y como tal, equivale al "par" que forma la fuerza cortante (Vj) absorbida por los patines multiplicada por la altura del perfil, h (medida a la línea media de los patines). Esto es,Ta=Vfh.

De (3) es posible inferir que la fuerza cortante (Vy) absorbida por los patines es:

donde:

De la ecuación diferencial de la elástica, el momento flector que se genera en los patines (Mj), está definido por,

Vinculado a la definición de momento torsional de alabeo (7^), se encuentra el concepto de Bimomento (Mo),que no es otra cosa que la magnitud estática proveniente del producto entre el momento flector (M~) que se genera en los patines y la altura h, del perfil. Esto es,

A partir de (6) es posible decir que el momento torsor de alabeo (7^) es igual a la primera derivada con respecto a x del Bimomento IMJ. En síntesis, el momento torsional total resistido por la sección transversal (torsión mixta) es la suma de la torsión de Saint Venant y la de alabeo, descrita por las ecuaciones (1) y (3), respectivamente. La primera, está siempre presente, mientras que la segunda depende de la resistencia al alabeo. Denotando el momento resistente torsional total por T*, se obtiene la siguiente expresión de la torsión mixta:

La solución de la ecuación diferencial de la torsión (7), es de la forma:

Donde k, es el parámetro torsional característico que se define como la constante que relaciona la torsión de Saint Venant con la de alabeo. Esto es,

En la ecuación 8 se evidencia la necesidad de determinar las tres constantes de integración A, B y C a partir de las condiciones de borde. Por su parte, se conoce como funciones torsionales las expresiones para "T.", "7^", "MJ y "6", descritas en las ecuaciones (1), (3), (6) y (8), respectivamente (Prandtl, 1903). Para definir completamente el comportamiento de un elemento prismático sometido a solicitaciones de torsión, es necesario conocer estas cuatro funciones torsionales. Suponiendo un punto m sobre la longitud de la viga donde se encuentra aplicado el momento torsional T, X la distancia a la izquierda (i) de m yX' la distancia a la derecha (d), sin precisar la condición de apoyo, la solución general que permite obtener los parámetros torsionales 6(x), 0 (x),

T, es:

El sistema de ecuaciones (10), suma las ecuaciones obtenidas en los dos intervalos definidos por el punto m. El momento torsional aplicado T* es absorbido por la torsión de alabeo, mientras el momento torsional de Saint Venant es igual en todos lados. Esto significa que:

En la expresión (11), T& y Tad, son respectivamente, el momento torsional de alabeo en el tramo a la izquierda y a la derecha, de m. Por resultar de interés práctico para este trabajo, se determinan a continuación las cuatro funciones torsionales para una viga simplemente apoyada en ambos extremos y el momento torsional aplicado en cualquier punto de la barra prismática. Se consideran apoyos que impiden la rotación y permiten el alabeo. Las condiciones de borde, son:

Reemplazando las condiciones de borde en (10), se tiene que:

Nótese que a partir de las anteriores expresiones, sihh(x-A) = sinh kX'.

La solución del sistema de ecuaciones definido para x=L, permite determinar el valor de los parámetros 0O' y To.Estos son:

Los resultados obtenidos para las cuatro funciones torsionales de interés son:

En el tramo izquierdo:

En el tramo derecho:

2.2 Variables que intervienen en la torsión de alabeo

El concepto de área sectorial co(s) es la base del estudio de la torsión de alabeo (Vallecilla, 2005). Permite obtener la posición del centro de corte de una sección e introduce los conceptos de momento estático sectorial (Seo) y momento sectorial de inercia (Ico). Estos dos parámetros, permiten calcular los esfuerzos de alabeo. Es posible decir que, la definición de área sectorial (co) es a la teoría de torsión de alabeo, como los conceptos de: área, momento de primer orden y segundo orden (ó de inercia) de una sección, son a la teoría de flexión. La coordenada que recorre la línea media del perfil, medida a partir de un punto 0 (punto nulo) hasta un punto P(s) se denomina coordenada sectorial S. El área sectorial (cajequivale entonces, al doble del área barrida por un vector QP (Q es un punto arbitrario contenido en el plano de la sección llamado polo auxiliar, que generalmente se hace coincidir con el centro de gravedad de la sección) al moverse un punto P (contenido en la sección), desde el punto nulo 0 u origen (por conveniencia 0 se escoge como un punto libre de la sección) hasta cierto valor S denominado coordenada sectorial (la coordenada S se mide a lo largo de la línea media del perfil desde el punto nulo 0 hasta el punto de referencia P(s) = P(y,z), esto es, de 0 a S se recorre la sección; S se mide desde el punto S = 0 (nulo) hasta el punto S = b, y el valor de b representa el perímetro de la sección). Si la rotación del vector QP se realiza en sentido contrario a las manecillas del reloj el incremento de área es positiva, en caso contrario será negativa. Se concluye, que el área sectorial rn(s) es función del arco de barrido S y depende de las posiciones del punto nulo 0 y el polo auxiliar Q. Es conveniente ubicar el polo auxiliar Q en el centro de gravedad de la sección y el punto nulo 0 en el eje de simetría (si existe); una vez escogidos, todas las distancias deben referirse a ellos (Feodosiev, 1980).

donde:

Po = Normal entre la tangente trazada por P que pasa por el polo auxiliar Q. Es positivo si la tangente describe una rotación antihoraria. Por resultar de interés práctico para este trabajo, se presenta a continuación tres alternativas de construcción del área sectorial co(s) para una sección I asimétrica.

Por integración numérica

En las ecuaciones (24) y (25), los subíndices i, k representan el valor inicial y final de la propiedad, respectivamente, y / la longitud.

tik = Espesor del tramo ik

lk = Longitud del tramo ik

£ o = Valores de las áreas sectoriales en los puntos iyk[L2]

y i, yk = Valores de la coordenada y en los puntos i y k zu Zk = Valores de la coordenada z en los puntos i y k I» 2<a(Z) = Momentos sectoriales de desviación [L5]

El centro de cortante (D), es el punto por el que una sección sometida a torsión pura rota y por el que debe pasar la resultante de las fuerzas aplicadas para que se produzca flexión sin que ocurra torsión (Amenzade, 1979). Las coordenadas del centro de cortante (D) de la sección son función de los momentos sectoriales de desviación y de los momentos principales de inercia (Kollbrunner, 1970). Si el plano de la sección es YZ (Z+ en dirección de la gravedad), las coordenadas del centro de cortante (Y& ZdD, pueden determinarse por medio de las siguientes expresiones:

El área sectorial del centro de cortante coD (s) se define como el área sectorial a>(s) referida al centro de cortante (D ) de la sección.

Donde:

pD= Distancia del centro de cortante D y la tangente trazada por un punto de la línea media de la sección P(y,z)

El momento estático sectorial Seo es función de co(s). Por lo mismo, dado que to varía linealmente, Seo es parabólico.

Por integración numérica:

En un perfil I, el momento estático sectorial máximo Seo, en los patines, es:

En la ecuación (33), Ay y tp son el ancho y el espesor del patín, respectivamente.

La función unitaria de alabeo © ¡f s) ó alabeo unitario referido al centro de cortante de la sección (D), se denomina también coordenada sectorial normalizada, es función del momento estático sectorial Seo, y queda descrita por la ecuación:

donde:

t = Espesor de la pared

A = Área de la sección [L2]

(¡Da = Área sectorial referida al centro de cortante (D) de la sección [L2]

La integral para el momento estático sectorial, descrita en la ecuación (34) es cero si la sección posee un eje de simetría y el punto nulo se ubica sobre el mismo. En este caso dicho punto no sufre desplazamiento en el sentido longitudinal, y Js ) = (D).

El momento sectorial de inercia, conocido también como constante de alabeo, se define por la ecuación (35):

Por integración numérica,

El alabeo se define como el desplazamiento |1 en la dirección del eje longitudinal (normal al plano de la sección) de todos los puntos de un miembro sometido a torsión pura. La ecuación (37) describe este desplazamiento.

donde:

Cº(x)= Función de desplazamiento. Representa el desplazamiento en x del punto s = 0.

En secciones con un eje (ó dos) de simetría, si S se mide a partir de este, el valor de Q(x) es nulo. En este sentido, cuando la sección no posee simetría se hace necesario calcularlo.

2.3 Esfuerzos debidos a la torsión

Retomando el apartado (2.1), los esfuerzos asociados a la torsión de Saint Venant Ts son de corte (xs), y los generados por la torsión de alabeo Tco, esfuerzos normales (oto ) y cortantes (too).

2.3.1 Esfuerzos debidos a la torsión de Saint Venantz

Estos esfuerzos cortantes están siempre presentes en la sección transversal de un miembro sometido a un momento torsional. Estos esfuerzos varían linealmente en el espesor de un elemento de la sección transversal y actúan en dirección paralela al eje del elemento. Son máximos e iguales, pero de dirección opuesta, en los dos ejes. El esfuerzo máximo se determina por la ecuación:

Los esfuerzos cortantes de torsión pura son mayores en los elementos de mayor espesor de la sección transversal.

2.3.2 Esfuerzos debidos a la torsión de alabeo

Estos esfuerzos (tensión (+) y compresión (-)) resultan directamente de la flexión del elemento debido a la torsión. Actúan perpendicular a la superficie de la sección transversal y son constantes en el espesor de un elemento de la sección, pero varían en magnitud en la longitud del elemento. Estos esfuerzos actúan en dirección paralela al eje del elemento. La magnitud de estos esfuerzos se determina por la ecuación:

Para un perfil I,

donde:

f= Momento de inercia del patín con respecto al eje ccntroidalZ. Estoes, jy = f¿ Y2 dA

Los esfuerzos cortantes de alabeo son constantes en el espesor de un elemento de la sección transversal, pero varían en magnitud en la longitud del elemento. Estos esfuerzos actúan en dirección paralela al eje del elemento. La magnitud de estos esfuerzos se determina por la ecuación:

Para un perfil I,

donde:

Af = Área del patín

2.4 Caso de estudio

Por ser de interés en ingeniería, se presenta en este trabajo el análisis por torsión de una viga metálica de un puente grúa, sometida a las cargas móviles propias de este tipo de máquinas. Los puentes grúa son equipos para elevación y transporte de uso muy común a nivel industrial. Básicamente se trata de una estructura elevada formada por una o varias vigas metálicas, con un sistema de desplazamiento de cuatro ruedas sobre rieles laterales, movidos por uno o más motores eléctricos. El movimiento longitudinal se lleva a cabo mediante la translación de la viga principal o puente a través de los carriles elevados. El movimiento transversal se realiza mediante el desplazamiento de un polipasto o carro sobre uno o dos carriles dispuestos sobre la viga principal (figura 7).

Se busca determinar los máximos esfuerzos normales y cortantes que se producen en la viga metálica de un puente grúa como el de la figura 7, sometida a la acción de las cargas móviles verticales P 1y P2 y horizontales H1 y H2, separadas una distancia de tres metros, como se ilustra en la figura 8(a).

Estas cargas poseen una componente vertical y otra horizontal, cuya resultante pasa por fuera del centro de cortante, configurándose así un caso típico de solicitaciones combinadas de flexo-torsión. Se supone que la resultante de las fuerzas horizontales se encuentra aplicada a una distancia de cuatro centímetros medidos a partir de la línea media del patín superior de la sección (figura 8(b)).

3. Resultados

La determinación de los esfuerzos debidos a la torsión supone el conocimiento de las propiedades geométricas de la sección, esto es, el área, la posición del eje centroidal y el momento centroidal principal de inercia. Utilizando un programa como p. ej. Ansys®, es posible obtener estas propiedades y otras como, la constante de alabeo, la constante torsional y coordenadas del centro de cortante. En la figura 9, se ilustra un esquema de la sección dibujada enAnsys y sus propiedades geométricas más importantes (en cm).

No obstante, para efectos académicos, a continuación se presenta el procedimiento completo que implica la obtención del centro de cortante. Con relación a la figura 8b, son evidentes, las características de la sección transversal del puente grúa, que se resumen en la tabla 1.

Nota: El riel no hace parte de la sección resistente por lo que no interviene en los cálculos.

Una vez conocidas las propiedades geométricas de la sección, se deben determinar las propiedades torsionales de la misma, lo que exige el conocimiento de la posición del centro de cortante (D) de la sección. Es claro de la simetría de la sección que la coordenada Y del centro de cortante es cero (Yd=0). En consecuencia, sólo es necesario determinar la coordenada Z del mismo (Zd), de acuerdo a la expresión (27).

No obstante, la solución de la ecuación (27) supone el conocimiento del momento estático de desviación /

El mismo, es función del área sectorial de inercia de la sección a (o) definido por la ecuación (21). Para el efecto, se escoge como polo auxiliar (punto Q) el centroide C de la sección y el punto nulo sobre el eje de simetría Z como se muestra en la figura 9a. Con estas definiciones se construye el diagrama de áreas sectoriales y el diagrama de la coordenada Y (figura 9b).

Es de interés recordar que el cumplimiento de la regla de la mano derecha, implica que las rotaciones del radio de referencia deben ser antihorarias. Esto explica el signo de las áreas sectoriales mostradas en la figura 10. Se resalta, sobre la importancia de una clara definición del sistema de ejes de coordenadas que definen la estructura. En este sentido, es evidente que el eje X apunta en la dirección longitudinal del puente grúa.

La teoría de áreas sectoriales suministra la ecuación (24) que permite calcular el momento estático de desviación Itoy). Teniendo en cuenta los signos de las áreas, se tiene, al sustituir los valores numéricos de la figura 10, en la ecuación (24):

Sustituyendo los valores numéricos respectivos en la ecuación (27), se obtiene la coordenada Z del centro de cortante de la sección (ZD)'.

El signo negativo indica que el centro de cortante (D) está 10.70 cm por encima del centroide (punto C), en la dirección negativa de Z. De acuerdo al sistema de referencia de la figura 8(b), las coordenadas del centro de cortante son (YD, ZD) = (0,-10.7). Una vez obtenida la posición del centro de cortante de la sección, es posible determinar la coordenada sectorial normalizada ú/S) descrita por la ecuación (34).

No obstante, como la sección tiene un eje de simetría (eje Z), la integral jb (5) t ds es cero, por lo cual (ofs) = cod(s). 0

En estas condiciones las distancias se miden ahora a partir del centro de cortante de la sección y conducen al diagrama de la figura 11, en el que se resumen los valores de la coordenada sectorial normalizada.

Por otra parte, es necesario determinar también los esfuerzos producidos por la flexión. Para el efecto se debe tener en cuenta que el tren de cargas es móvil, lo que exige determinar la posición de las dos cargas que producen el máximo momento en la luz, al igual que los momentos torsionales debidos a la excentricidad de las cargas verticales y horizontales.

Según las excentricidades de las cargas impuestas, e =lcm y ez=26.1 cm, en las direcciones Y y Z respectivamente (referirse a los esquemas de la geometría de la sección (figura 8(b)) y de la posición del punto de aplicación de las cargas (figura 12), es claro que los momentos torsionales debidos a las cargas horizontales y verticales (P1, H1) y (P2, H2), son:

Debido a(Pl yHl):

Tl=P1ey+H1ez=90xl+4x26.1=194.4kN.cm

Debido a (P2 y H2):

T2=P2ey+Hjez=60x 1+2x26.1=112.2 kN.cm

Es importante tener en cuenta, que la determinación de la posición de las cargas que producen el máximo momento flector se lleva a cabo a partir del siguiente enunciado: "el momento flector bajo un tren de cargas móviles es máximo, cuando el punto medio entre la carga y la resultante de cargas móviles que actúan en la luz, coincide con el punto medio de la viga". Esta situación se resume en las figuras 13 y 14.

De acuerdo a la figura 13,

Resultante de fuerzas verticales:

P=P1 +P2 = 90 + 60= 150kN

Posición de la resultante P: Apartir de P1,

xp = 60x3__150 = 1.20m = 120cm

Queda claro, que la media distancia entre la carga P 1y P es 0.6m (60cm) y entre la carga P2 y P es 0.9m (90cm).

Es conocido, que del análisis de solicitaciones debidas a las cargas móviles se deben estudiar los momentos máximos bajo cada una de las cargas puntuales que actúan sobre la estructura. En consecuencia se resume en la figura 14 los momentos máximos (My) producidos por la carga viva vertical y se concluye que la máxima solicitación se encuentra bajo la carga puntual vertical P1 de 90 KN (posición 1). Por resultar de gran interés académico este trabajo, se han querido ilustrar los diagramas de cortante, momento y torsión haciendo uso del programa SAP2000 ® (Figuras 15,17 y 20).

De igual manera, se procede con las cargas horizontales tal como se resume en la figura 15.

Resultante de fuerzas horizontales: H=H1+H2=4 + 2 = 6 kN

Posición de la resultante H: ApartirdeHl, xh = ~ = l-0m = 100 cm

Queda claro, que la media distancia entre la carga H1 y H es l.Om (lOOcm) y entre la carga H2 y H es 2.0m (200cm).

Del análisis precedente se concluye que el máximo momento flector (My=513kN.m=51300kN.cm) debido a las cargas verticales se presenta a una distancia x=7.4m (posición 1, figura 14(a)), por lo cual, el momento (Mz) correspondiente para cargas horizontales es:

En estas condiciones es posible determinar los esfuerzos normales resultantes por flexión (en x=7.4 m), empleando la ecuación de flexión biaxial (44).

Esto es,

Recordando que los momentos flectores máximos en KN.m son My=513 y Mz=20.8 y las propiedades geométricas de la sección (tabla 1), se obtienen los valores de los esfuerzos normales en los puntos de interés de la sección, representados en la figura 18.

Sustituyendo los valores numéricos en la fórmula de la flexión biaxial, ecuación (44), se concluyen los resultados mostrados en la tabla 2. Según la convención de signos, son negativos los esfuerzos de compresión.

Una vez determinados los esfuerzos debidos a la flexión biaxial es necesario calcular los esfuerzos producidos por la torsión, lo que exige conocer, en primer lugar, la coordenada normalizada de alabeo. La figura 11, resume los valores de la coordenada normalizada de alabeo en los puntos de interés de la sección. El cálculo de esta coordenada se realiza de acuerdo con los principios de la teoría de las áreas sectoriales. Acto seguido deben determinarse las propiedades torsionales de la sección. Estas son, la constante torsional K, el momento sectorial de Inercia Ico y el parámetro torsional característico k. La constante de torsión de Saint Venant ÁT para la sección transversal en estudio, se calcula por medio de la ecuación (42).Esto es,

El momento sectorial de inercia Ico, viene dado por la ecuación (36). Sustituyendo los valores numéricos, se obtiene:

La constante que relaciona la torsión de Saint Venant (TS) con la torsión de alabeo (Tco ) es el parámetro torsional característico ( k ), cuya expresión se referencia en la ecuación (9). Si se supone que las vigas del puente grúa son de acero de módulo de elasticidad jt=200000MPa (relación de Poisson v« 0.3), el módulo de elasticidad a cortante (G) es:

Esto significa que:

Una vez determinadas las constantes que describen el comportamiento torsional del puente grúa, es posible obtener las funciones torsionales. Para el efecto, se muestra en la figura 19 las solicitaciones por torsión debidas a las cargas horizontales y verticales, que definen el esquema estático torsional. Los momentos torsionales son, Tl=1.944 kN.m debido a (P1 y Hl) y T2= 1.122 kN.m debido a (P2 y H2).

En particular, interesan las funciones torsionales Meo, Ts, Tco y 0, para x=7.4 m, punto en el que las solicitaciones por flexión son máximas (A=7.4 y ? A 8.6).

La primera función torsional que es necesario determinar es el Bimomento (Meo), cuyo comportamiento es descrito por las ecuaciones (13) y (17), para las dos zonas en las que se ha dividido la viga del puente grúa.

Zona I (Tramo izquierdo)

La segunda función torsional corresponde a la torsión de Saint Venant (Ts), descrita por la ecuación (13):

En estas condiciones es posible determinar los esfuerzos normales de alabeo en x=7.4m. De acuerdo con la ecuación (39). Los datos que alimentan la expresión son, el Bimomento (Mao), el momento sectorial de inercia (Ico) y la coordenada sectorial normalizada oN(s) . De acuerdo a esto, se definen los puntos de interés de la sección presentados en la figura 21.

Sustituyendo los valores numéricos en la ecuación (39) se obtienen los esfuerzos normales de alabeo en los puntos de interés de la sección. Esto es:

De la misma manera es posible obtener los esfuerzos cortantes en la sección ax=7.4m. Estos esfuerzos cortantes se deben a la fuerza cortante que actúa en la sección y a la torsión de alabeo. Los esfuerzos debidos a la fuerza cortante se calculan de acuerdo con la teoría clásica de la mecánica de sólidos, tal como se indica en la ecuación (46).

Q=AZ (47)

El flujo de corte Q de la ecuación (47), calculado para cada una de las zonas de interés de la sección (fibra inferior FIy fibra superior FS de los patines, y el alma) se desarrolla a continuación:

La figura 23 resume la distribución de esfuerzos cortantes en la sección ax=7.4 m.

Igualmente, es necesario calcular los esfuerzos cortantes debidos al alabeo Tm, cuya expresión viene dada por la ecuación (41).

De los cálculos precedentes,

Twx-7,4)=1.336 KN.m = 133.6 KN.cm. Además, el momento estático sectorial Sa , en los patines (ver figura 24) dado por la ecuación (33) es:

En consecuencia, se obtienen los siguientes esfuerzos cortantes debidos a la torsión de alabeo (ecuación 38):

Esfuerzo cortante debido a la torsión de alabeo en el patín superior:

4.Conclusiones

Cuando la línea de acción de la resultante de fuerzas no pasa por el centro de cortante de una sección se producen momentos torsionales que causan esfuerzos que es necesario evaluar.

La torsión en elementos estructurales puede ser producida en forma directa por las acciones exteriores, o puede presentarse al iniciarse el pandeo de un miembro originalmente recto sometido, por ejemplo, a flexión. El desplazamiento lateral del eje y las rotaciones de las secciones transversales que caracterizan el pandeo de las vigas ocasionan momentos torsionantes; la resistencia de la viga aumenta cuando crece su oposición a los desplazamientos laterales lo que depende, entre otras cosas, de su resistencia a la torsión.

Exceptuando las barras de sección transversal circular, maciza o hueca, todos los elementos estructurales sometidos a torsión pura se alabean, es decir, los puntos situados en planos originalmente normales al eje de la barra experimentan desplazamientos variables paralelos a ese eje, lo que ocasiona que las secciones transversales inicialmente planas dejen de serlo.

El alabeo de la sección se traduce en una distorsión de la misma y se caracteriza por la presencia de esfuerzos normales.

Los esfuerzos normales producidos por la restricción al alabeo están acompañados por esfuerzos tangenciales, que contribuyen a resistir el momento de torsión exterior, de manera que éste no es equilibrado sólo por esfuerzos cortantes de Saint Venant, como sucede cuando el alabeo es libre. En otras palabras, tanto los esfuerzos tangenciales simples como los debidos a la restricción al alabeo contribuyen a resistir el momento exterior.

Para que aparezcan los esfuerzos normales longitudinales, no es necesario impedir totalmente el alabeo de alguna sección transversal; basta con que, ya sea por las condiciones de apoyo o de carga, o por una combinación de ambas, el alabeo no se presente libremente y varíe de unas secciones transversales a otras, lo que ocasiona deformaciones longitudinales de las fibras.

Los esfuerzos producidos al restringir el alabeo de barras de sección transversal maciza no circular son mucho menores que los de las secciones abiertas de paredes delgadas; además, las piezas macizas no se emplean en estructuras de acero. Por estas razones, es de gran importancia el estudio de elementos con secciones transversales del segundo tipo.

Teóricamente, el cálculo de los esfuerzos debidos a la torsión de alabeo se lleva a cabo mediante la teoría de áreas sectoriales.

En algunos casos, los esfuerzos debidos a la torsión pueden ser mayores que aquellos debidos a la flexión, por lo que su determinación es esencial para un correcto dimensionamiento de las estructuras.

5. Referencias Bibliográficas.

1. Amenzade, J. A., 1979, Theory of Elasticity, MIR, Moscú.

2. Basler, K., Kollbrunner, C. F., 1975, Dünnwandige Stabe, Springer Verlag, Muenchen.

3. Britvec, S. J., 1973, The Stability of Elastic Systems, Pergamon Press Oxford, NewYork.

4. Feodosiev, V. I., 1980, Resistencia de Materiales, Mir, Moscú.

5. Filonenko & Borodich, 1963, Teoría de la Elasticidad, Platina, Buenos Aires.

6. Galambos, T. V., 1968, Structural Members and Frames, Prentice Hall, New Jersey.

7. Gjelsvik, A., 1981, The Theory of Thin Walled Bars, John Wiley, NewYork.

8. Green, A. E., Zema, W., 1968, Theoretical Elasticity, Oxford University Press, NewYork.

9. Hartog, D., 1980, Advanced Strength of Materials, Dover Publications, New York.

10. Kollbrunner, C. F., Basler, K., 1970, Torsion. Application a l'étude des structures, Spes, Lausanne.

11. Kollbrunner, C.F., Basler, K., 1969, Torsion in Structures. An Engineering Approach. Springer Verlag, Berlín.

12. Monleón, C., 1999, Análisis de Vigas, Arcos, Placas y Láminas, UPV, España.

13. Mushkhelishvili, N. I., 1953, Some basic problems of the mathematical theory of elasticity, P. Noordhof Ltd., Moscú.

14. Ortiz, L., 2002, Elasticidad, McGraw-Hill, España.

15. Prandtl, L., 1903, Zur torsion von prismatischen staben, Physikalische Zeitschrift, Berlín.

16. Reismann, H., Pawlik, P., 1980, Elasticity. Theory and Applications, John Willey, NewYork.

17. Timoshenko, S. P., Gere, J., 1961, Theory of Elastic Stability, McGraw-Hill, NewYork.

18. Timoshenko, S. P., Godier, J. N., 1951, Theory of elasticity, McGraw-Hill, New York.

19. Timoshenko, S. P., 1977, Advanced Strength of Materials. Dover Publications. New York.

20. Vallecilla, C. R., 2005, Torsión en las construcciones, Unisalle, Colombia.

21. Vlassov, V., 1948, Pieces Longues en Voiles Minees, Eyrrolles, París.

22. Wang, C. T., 1953, Applied Elasticity, McGraw-Hill, New York.