Mauro Montealegre Cardenas1,Jasmidt Vera Cuenca2 y Edgar Montealegre Cardenas.3
En este trabajo analizamos el problema Stefan de dos fases permitiendo irregularidades en la frontera libre, el cual requiere el tratamiento implícito de la interface a través de formulaciones débiles de la entalpia, para construir funcionales de costos ∫(u,n(u),v(u)) sujetos a un control externo u en un dominio limitado Ω ⊂ RN (N≥ 2) el cual tiene borde suave ∂Ω, y para 0 < T< ∞ fijo Q ≡ Ω X [0,T], ∑ ≡ ∂ Ω X [0,T]
Palabras claves: Ecuación del calor, problemas con frontera libre, control óptimo, bifurcaciones, funcionales de costo, entalpia, crecimiento de tumores. segregación espacial.
In this paper wc analyze the two-phase Stefan problem allowing the free boundary irregularities, which requires implicit treatment of the interface through weak formulations of the enthalpy to construct cost functional ∫(u,n(u),v(u)) subject to external control u in a limited domain Ω ⊂ RN (N≥ 2), that has soft edge ∂Ω and to for 0 < T< ∞ fijo Q ≡ Ω X [0,T], ∑ ≡ ∂ Ω X [0,T]
Keywords: Heat equation, problems with free boundary, optimal control, bifurcations, cost functional, enthalpy, tumor growth. spatial segregation.
Este estudio se refiere al conocimiento de los modelos matemáticos en los cuales la dinámica dispersiva sobre la frontera afecta su ubicación espacial, son los llamados problemas con frontera libre, una área de la matemática aplicada con intercepciones en ecología, biología celular, físico - química y economía.
El método para abordar estos estudios, una vez concretado el modelo con sus condiciones iniciales, de frontera y la llamada condición de Stefan, consiste en conocer la función que describe el intercambio de energía en esa frontera libre, hasta el cambio de la forma en su frontera; y el estado del calor, entendido en términos de la energía que evoluciona en el dominio espacio - temporal.
Pero es conveniente describir los cambios estructurales de las soluciones, esto es, las bifurcaciones que surgen en estas soluciones y el control que se pueda ejercer en todo este proceso. Por ello el proceso de solución cae en el contexto del control óptimo a funcionales de costo, cuyo mínimo restringido es relevante para la descripción del proceso en busca de resultados deseados.
En términos de los procesos matemáticos necesarios para este tipo de estudios realizamos: análisis de estabilidad lineal en tomo de estados de reposo, con buenas aproximaciones a la estabilidad no lineal.
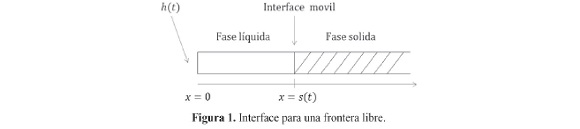
Sea la interface, ver figura 1, entre dos estados de la materia, la cual se coloca a través de los siguientes subconjuntos del espacio - tiempo:
permitiendo que la frontera libre alcance uno de los extremos x = 0 y x = d, en este contexto el modelo matemático sobre el problema de Stefan unidimensional lineal esta constituido por el siguiente sistema.
Para esta función s ∈ C([0,T]), notamos el siguiente subconjunto,
y la solución de este problema (1) es el par de funciones (s,u) que tiene las siguientes propiedades.
La solución explícita del sistema (1) se obtiene en términos de la siguiente función v,
Aqui erf denota la función de error. Para cada C > 0 arbitrario y a > 0 tenemos la siguiente expresión para u (x,t):
y además s(t) = 2a √t. Asi u > 0 en Qs,T . además verificamos que.
Por ello,
si y solo si
Observe que en el contorno fijo x = 0 podemos seleccionar una de las condiciones
Asi hemos demostrado que cuando a > 0 se tiene.
es la solución del problema (1), lo cual se resume en la siguiente figura (2):
En [1] se presenta el siguiente problema: Sean u(x, t) la temperatura del líquido, s(t) la posición de la interface entre dos estados de la materia en un tiempo t. El problema inverso consiste en dado s(t)∈ C∞[0,T] hallar u(x,t) \in C(Dt∩Bt) acotada, con uxx , ut ∈ C(Dt) ; dado que h t u0(x) las temperaturas en x = 0 para t > 0, cuando t = 0 para todo x, que satisface:
Donde el dominio DT tiene la siguiente frontera:
tal como se ilustra en la figura 3.
La condición de Stefan dice que la energía calórica que aparece en la interface es totalmente utilizada en el proceso de fusión.
Solución: Como x2n es denso en L2, consideremos una solución para el problema (2) análoga a la siguiente serie.
en particular asumimos soluciones del siguiente tipo
de lo cual se obtienen las siguientes fórmulas de recurrencias,
Para n > 20 a0 = O porque u(s(t), t) = 0, at = s.
Estas conclusiones son necesarias y suficientes, esto es dados s(t), h(t), uo(x) existen unívocamente an y u(x,t)
Observamos que el radio de convergencia de (3) tiene el siguiente acotamiento:
En cuya prueba se usa el siguiente Lema técnico.
Sobre la convergencia de la serie (3), tenemos el siguiente Teorema:
En esta sección consideramos el problema de control que consiste en maximizar la cantidad de mezcla en la superficie de contacto de la mezcla en el problema de Stefan donde el flujo de calor total en la frontera es la variable de control.
Si u0(x) > 0, δ(x) > 0, h(t) > 0 consideremos el problema de Stefan con una fase que consiste en encontrar (u,s) satisfaciendo.
Para ux(s(t),t), proponemos soluciones perturbadas (u∈, s∈) para el parámetro ∈ > 0:
En (5) si δ(x) > 0, entonces γ(t) > 0, funciones medióles con ∫0T g(t) dt < ∞ y ∫oT γ(t) dt < + ∞ y a (5) le asociamos el siguiente problema πε de control óptimo:
Se puede probar que:
y además
Prueba: Usamos funciones del siguiente tipo:
Es fácil ver que v(x, t) satisface las siguientes condiciones,
y por ello (6) tiene las siguientes relaciones:
Expresamos w en términos de su función de Green G(x,t;ξ,τ), τ < t, en el dominio
esto es, w(x,t) = ∫otw(0,τ) Gx(x, t; 0, τ) resultando que G(x, t; ξ, τ)- δ ξ cuando τ ⇑ t, donde δx(ξ) es la medida de Dirac centrada en x = ∈.
γ(t) = w(s(t)t) esto es
puesto que G(x,t;0,τ) = 0. el principio del máximo dice que Gξ(x.t,0,τ) <0 en 0 < x ≤ s(t), τ < t; entonces γ(T) es el máximo si y solo si δ(s) es la medida de dirae centrada en s = 0 veces A.
El Problema General de control es el siguiente.
En (9) función de control h(t) la podemos considerar variando en el conjunto siguiente,
Si hacemos u = uh s = Sh se propone resolver el siguiente problema π:
El modelo da respuesta al siguiente problema: Sea el dominio acotado Ω ⊂ R N (N ≥ 2), con frontera acotada ∂ Ω, 0 < T < ∞ Q ≡ Ω x ]0,T[∑ ≡ ∂ Ω, donde buscamos un par (η, θ) que satisfacen el siguiente sistema:
Aquí θ = θ(x,t) representa la temperatura, η = η(x,t) representa la entalpia y y es un gráfico maximal y monótono como el siguiente,
con H(θ) = 0 si 0< θ, Hθ= [0,1] si θ = 0; H (θ) = 1 si θ > 0, λ > 0 representa el calor latente y b R → R es una función estrictamente creciente y suficientemente suave.
La condición inicial no está bien definida y la condición de contorno Neumann en (10) contiene la variable de control u = u (x, t) que corresponde al flujo de calor en la frontera. El control puede representar un coeficiente de calor o la temperatura exterior y es elegido en un subconjunto admisible U de L1 (∑).
La interface se ubica en el conjunto de nivel φ ≡ {θ = 0 } que separa la zona de fase liquida {θ > 0} con la zona de fase sólida {θ< 0} y es controlada implícitamente.
Específicamente consideramos la frontera libre controlada del tipo
El funcional para el costo se construye con la temperatura θ =θ (u) y en la mayoría de los casos que contiene cantidades de uno de los siguientes tipos:
Donde θ denota una función prescrita y p una función de peso apropiado. Por ejemplo, un principio big-bang para el problema de una sola fase acostumbrada para el control a través de la condición de Neumann.
Asumimos η0 ∈ L∞(Ω)) y h = h(x, í, θ,u) es una función Caratheodoiy, es decir, continua en las variables θ y u, para casi todo (x, t) ∈ ∑ y L2(∑) Para cada (θ,u) Y satisface una condición de signo compatible con el principio del máximo débil, a saber,
para algunas constantes positivas grandes μ,ρ > 0. En particular, esto es válido para el flujo lineal
En estas condiciones tenemos la siguiente proposición,
Por otra parte, si {η,θ) y {η_n, Θn} denotan las soluciones correspondientes a diferentes datos, u y un respectivamente, entonces
se tiene que ηn → η en L∞ (Q) débil y θn → θ en Lp(Q) -fuerte (∀ < ∞) y en L2(0, T, H1(Ω)) - débil.
Observación: Como consecuencia inmediata de esta proposición hay dependencia continua con respecto al control optimo u de un funcional de costo semicontinuo inferiormente j(u,η(u), θ(u) ) u en conjuntos admisibles U ⊂ L∞(∑).
En general, el conjunto de nivel {θ = 0} puede tener medida de Lebesgue distinta de cero. Llamamos como región blanda al conjunto medible,
y denotamos por |A| la medida de Lebesgue W-dimensional de A ⊂ Ω . Inicialmente se considera s'olo el caso en que se puede evitar la region blanda, y consideramos los siguientes conjuntos admisibles para controles:
Sea ∧ ⊂ Q cualquier subconjunto medible de la zona liquida y su función característica, para ello consideramos el siguiente funcional para el costo
Donde χ (u)= χ{θ(u) > 0} es la función característica de la zona líquida para u ∈ L∞(∑) y el siguiente teorema de control:
Sea u ≡ 0 la temperatura de solidificación y fusión representada en la siguiente ecuación de difusión no lineal:
Donde Q = ]0,T[ X Ω, Ω ⊂ RN acotada con frontera regular Γ.
Si Γ (t) es la superficie que separa las dos fases en el momento t ∈ [0,T], esto es la frontera libre y la condición de Stefan para la siguiente ley de conservación de energía,
Con ρ la densidad y L el calor especifico latente. Adicionamos condiciones iniciales y de frontera. La solución débil de este problema es.
Donde
v = u|Γ y ∈ β (u) es la entalpia con valor inicial y0,
Es un gráfico maximal monótono.
Este F.B.P se puede expresar con desigualdades variacionales, que conducen al siguiente problema de optimización:
En dos dimensiones esta restricción es
Con ya∈ L2 (Ω)N, ƒ ∈ L2(Ω), E ⊂ Ω y D dominio variable tal que E ⊂ D ⊂ Ω .
El crecimiento de tumores localizados básicamente se describe mediante el siguiente modelo:
Donde k es la curvatura de la superficie de contacto, σ es la concentración del nutriente y ρ la presión interna que causa el movimiento del material celular. La version mas simplificada es la siguiente:
Sujeto a,
donde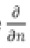 
es la derivada normal, k es la curvatura de ∂Ω; σ, γ son constantes positivas. Se puede verificar que si 
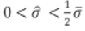existe una única solución de (17)-( 18) que es radialmente simétrica:
donde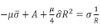 
, además 
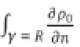y existen las siguientes soluciones no radiales (σ∈,ρ∈, Ω∈, Γ∈), que bifurcan de (σ0, ρ o):
La cual son convergentes y son soluciones analíticas en (γ, θ, ∈), esto es en (x,y, ∈) para (x,y) en una vecindad de {γ ≤ Ro} y |∈| pequeña. En particular si ƒ1(θ) = cos(lθ), l ≥ 2 y el punto de bifurcación es determinado unívocamente por {μ, σ, σ, l}, γ0 = ƒ(Ro).
Las ecuaciones de bifurcación se obtiene mediante la siguiente función parametrizada de Lyapunov-SctimidL
F(λ,u) = 0;u ∈ X Banach, λ ∈ R con ƒ(λ,0) ≡ 0 para todo λ ∈ R.
Un punto de bifurcación (λ∈,0) es un punto en el cual existe una o múltiples soluciones no triviales λ = λ(∈), u =u(∈) con λ(0) = λ0 y u (0) = 0,
Con operador linealizado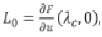 
resultando que L0 es un operador Fredholm con índice cero, con espacio nulo ,N(n= dim N < ∞) y rango R0.
Sea P la proyección de Y en N, Q = I - P es la proyección de Y en Ro, Si descomponemos u = Pu + Ou v proyectamos F(λ, u) = 0 en N y R0. conseguimos el siguiente sistema de ecuaciones.
donde θ = P(u), ψ = Q(u).
Observamos que K(λ0, 0,0) =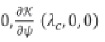 
= QL0 ; lo que significa que K es un isomorfismo de QX en QY, y por el teorema de la función implícita, ψ = ψ(λ ,θ), lo que sustituimos en (22) para alcanzar la siguiente ecuación de bifurcación:
la expresión (23) resulta ser un sistema de n ecuaciones.
Este método para obtener la ecuación de bifurcación no se puede aplicar directamente a problemas de frontera libre pues se requiere un dominio fijo y un nuevo T.F.I.
Para ilustrar esta limitación tomemos N = cos(lθ), y como Pu ⊥ Qu, entonces,
para infinitas translaciones de γ = R0.
Como
se excluyen soluciones pares en θ:(ƒj(θ), σj(γ, θ) Pj(γ, θ)) las cuales son analíticas en variables espaciales y en ∈ = 0. Además (**) implica Y2n+1 = 0 para todo n ≥ 0, y2n son unívocamente determinadas por las condiciones consistentes que deben ser satisfechas por los coeficientes de cos(lθ) y ∈2n+1
1. William B. Dumbar and Nicolas Petis. Boundary control of andnonlmeal stefan problem. ControL Optimization and calculus of sanations, 2003, vol. 9.
2. Yri A. Kuznetzov; Elements of applied Bifurcation Theory: Springer 2010.
3. SIAM J Non linear optimal control problems in heat conduction. . Control and optimization, vol. 21 No. 6. November 1983.
4. A Dollmamand A. van Harter Non linear dynamics and pattern formation m the natural environment. Longman. 1995.
5. Philip Holmes; Turbulence. Coherent Structures Dynamical Systems and Symmetry': Cambridge, Monographic on Mechanics. Cambndge. 1996.
6. J. F Rodnsuez and B. Zaltznaarc Free Boundary optimal control m t Math.. 88(1996).Ser. Num.
7. Peter Grindrod; The Theory and applications on Reaction-Difussion Equations. Patterns a Wave. Oxford 1996.
8. Femando Rertich, Shape deformations and Analytic continuation m free Boundary7 Problems. International Senes of Numerical Mathematics. vol 147,265 - 286.
9. Rebecca Hoyle; Pattern Formation. Cambridge, 2006.
10. Martin Golubitsky. Dan Luss and Steven Strogatz; Pattern Formation Continuos and Coupled Systems, Springer 1999.
