Alfonso Ramos1, Mario G. Trujillo2 y Jaime Izquierdo3
Como una fonna alternativa a los métodos convoicionales para realizar análisis de estabilidad de taludes, este artículo presenta una revisión bibliográfica de algunos procedimientos para modelar los flujos de material desagregado que parten desde la mecánica de medios continuos (perspectiva Eulenana), conservación de masa y momentum, de las que se selecciona la metodología propuesta por Iverson & Denlinger en el 2001. Esta metodología supone el comportamiento de una mezcla de fluido Newtomano y sólido cusa interacción fiicdonal es representada por la ley Coulomb. La ecuación de momentum es simplificada de tal forma que permiten generar una solución analítica, a la cual se le realizó un análisis de sensibilidad de acuerdo a cada uno de los parámetros de entrada. Los resultados del análisis de sensibilidad muestran que los parámetros que más influyen en el modelo son el ángulo de talud, el ángulo de fricción del lecho y la fracción de presión de poros, ya que determinan la estabilidad del talud. En caso de que el talud se desplace las variables que más influyen son la viscosidad dinámica y el espesor de flujo. El modelo simplificado se puede utilizar para el cálculo por etapas de la velocidad y el desplazamiento del centro de masa, por lo que sirve como insumo para evaluar la vulnerabilidad de infraestructura afectada por flujos de material desagregado.
Palabras clave: Flujos de material desagregado; Modelación; Análisis de sensibilidad.
As an alternative to conventional methods for slope stability analysis, this paper presents a literature review of procedures to model the disaggregated material flows that start from the continuum mechanics (Eulerian approach), conservation of mass and momentum, from which select the methodology proposed by Iverson & Denlinger m 2001. This methodology assumes the mixing behavior of a Newtonian fluid and solid whose frictional interaction is represented by Coulomb. The momentum equation is simplified in such a way that can generate an analytical solution to which was performed a sensitivity analysis according to each of the input parameters. The results of the sensitivity' analysis shows a general behavior of the model which tends to a constant speed after very long time and never stops as an effect of assuming an angle of the flow path and other parameters are constant. The simplified model can be used for the stepwise calculation of the speed and the displacement of the center of mass. Also, this simplified method can be used as input for nsk assessment by’ disaggregated material flow’s. The most important parameters in the model are the slope angle, bed friction angle and the fraction of pore pressure, as they determine the slope stability. In case the slope is moved most influencing vanable is the dynamic viscosity and the thickness of flow, as they cause which the flow has a change in the acceleration from the beginning
Key words: Disaggregates material flows; Modeling; Sensibility analysis.
Las zonas montañosas tropicales son muy susceptibles a sufiir movimientos en masa, debido a que generalmente se reúnen cuatro de los elementos más importantes para su generación: gradiente topográfico, sismicidad, meteonzación y lluvias intensas (Suarez, 1998).
Dentro de la clasificación de los movimientos en masa se encuentran los flujos, los cuales pueden ser lentos o rápidos dependiendo del contenido de humedad, de los tipos de material trasportados y la pendiente de la trayectoria del flujo. De igual forma dependiendo del tamaño del material transportado durante el flujo, se puede clasificar en flujos de roca, flujos de detritos, flujos de suelos y flujos de lodos (Suarez, 1998). De una forma general se denominarán como flujos de material desagregado a los flujos de lodos, flujos de detritos y flujos de suelos.
En Colombia están registrados de forma generalizada todos lo acontecimientos que comprende el concepto de movimientos en masa. Entre enero de 2011 y enero de 2012 se reportaron en total 1.463 evaitos de movimientos en masa en todo el pais, que dejaron 266 muato, 200 heridos, 251 desaparecidos y 85.260 viviendas destruidas. El departamento que más reporto movimientos en masa en este penodo fue el Huila con 208 eventos iJDEAM, 2012). Aproximadamente el 42% (Figura 3) de desastres causados por movimientos en masa en Japón entre los años 1989 y 2007, son atribuidos a los flujos de detritos (Shiestha, et al., 2008): de igual forma los flujos de detritos representan el 32% (Figura 4) de 252 casos de movimientos en masa de la cuenca vertiente al embalse de Rules (Granada-España) (Peralvarez. et al., 2008).
Para poder prevenir estos desastres, se elaboró el mapa de amenaza por fenómenos de remoción en masa de Bogotá D.C. en 1999, utilizando dos técnicas de evaluación: una heurística llamada Sistema de Evaluación Semicuantitativo (SES) que evalúa ocho parámetros cualitativos, siendo fijado un intervalo de variabilidad de acuerdo con la influencia de cada uno; y otro geomorfológico llamado Metodología de Taludes Naturales (MTN) desarrollada por Tomas Shnk en 1997 que consiste en mediciones en el terreno de altura y longitud en segmentos de ladera, variables que están ligadas a una relación funcional básica (Vargas, 2000).
Estos métodos y algunos más tradicionales realizan muchas suposiciones, como que el material es rigido, isotrópico, homogéneo, los efectos de borde son despreciables y el modo de falla es rotacional en la mayoría de los casos (Suarez, 1998). Estas suposiciones están establecidas para los deslizamientos, que son movimientos cuyo modo de deformación no es desagregada, sino que se produce al ceder una o varias superficies de rotura bien definidas, desplazándose la masa en conjunto, sin entremezclarse los materiales (Peralvarez, et al., 2008; Suarez, 1998). Este modo de falla no ocurre siempre, ya que un gran porcentaje de movimientos en masa lo hace de forma desagregada. Además estos métodos solamente establecen que tan estable es el talud, y en caso de que exista inestabilidad no se puede conocer otras variables de interés como: ¿a qué velocidad se desplaza el flujo? o ¿cuál será la distancia que recomerá desde el inicio de flujo hasta la deposición?
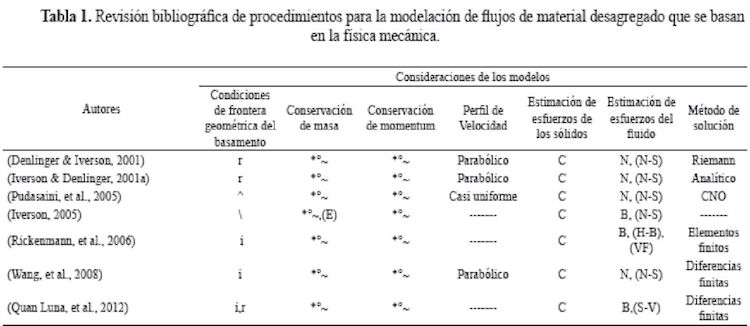
Debido a lo anterior, se crea la necesidad de abordar el problema de flujos de material desagregado desde una perspectiva alternativa (mecánica de medios continuos) a las convencionalmente adoptadas. Para ello, se realiza una revisión bibliográfica de metodologías basadas en la física mecánica y reglas matemáticas, de las cuales se seleccionó la propuesta de Iverson & Denhnger (2001) que presenta una solución analítica de las ecuaciones.
r: Superficie curva, A: Superficie curva y retorcida, Superficie Plana. L Superficie irregular, *: Se supone inconrpresibilidad. °: Teoría de mezcla, Teoría de la profundidad promedio, E: Ecuación especial de conservación de masa (Iverson, 2005), C: Teoría de fricción de Coulomb, N: Huido Newtoniano, B: Modelo de Bingham, N-S: Modelo de Xavier-Stokes, H-B: Modelo teológico de Herschel-Bulkley, VF: Relación de fricción del fluido Voellnry, S-V: Modelo de Samt-Venant CNO: Esquema Central No Oscilatorio.
Después de realizar la clasificación de algunos procedimientos para la modelación de material desagregado, se seleccionó el procedimiento desarrollada por Iverson & Denlmger (2001). Dicha selección se debe a que su desarrollo se fundamenta desde la flaca mecánica y las reglas matemáticas para modelar el comportamiento de estos procesos. Estas ecuaciones describen el comportamiento del flujo de material desagregado desde el inicio hasta la deposición, y requieren como parámetros de entrada las condiciones unciales, topografía de la trayectoria, ángulo de fricción interna y de los granos sólidos del lecho, viscosidad del fluido, densidad de mezcla y la presión de poros.
Procesos como los flujos hiper-concentrados podrían ser descritos por el modelo de Iverson & Denlinger (2001), siempre y cuando se tenga en cuenta que deben existir esfuerzos cortantes por fricción entre sólidos, en el caso en que la concentración de sólidos disminuya de tal forma que la interacción entre sólidos no sea fnccronal, smo por colisiones entre granos, esta formulación no sería la adecuada para este tipo de proceso.
Tanto los procesos como deslizamientos traslacionales y flujos de suelos cuyo contenido de agua es menor que los flujos hiper-concentrados, flujos de lodos y flujos de detritos, también pueden ser descritos por el modelo, siempre y cuando se tenga presente que la variación de la presión de fluido es lineal desde un máximo en el lecho, hasta cero en la superficie del flujo.
Después de plasmar desde la mecánica de medios continuos el comportamiento de los flujos de material desagregado se tiene como resultado la ecuación de momentum en la dirección x (1).
Los términos en el lado derecho de la ecuación 1 se agrupan por linea según el tipo de esfuerzo. De esta manera, la primera linea representa el esfuerzo constante basal, la segunda linea representa el esfuerzo longitudinal normal, las tercera linea representan el esfuerzo cortante transversal, y la cuarta linea representa el esfuerzo de conducción debido a la fuerza gravitatoria del cuerpo.
La solución analítica de la ecuación no lmeaL hiperbólica (1) se puede obtener para algunos casos especiales. El balance de momentum en la dirección y es inmaterial y el momentum en la dirección x es principalmente simplificado. Si se tiene una masa de mezcla uniforme con movimiento verticalmente inestable, espesor constante (h=H) descendiendo por una pendiente sin gradientes de velocidad en la dirección x y y, solamente con respecto al tiempo, y el tareno es un plano inclinado, la ecuación de momentum en la profundidad promedio en la dirección x es reducida a:
Donde
Siendo la ecuación 4 un parámetro que represorta la fuerza motriz gravitacional normalizada menos la resistencia debido a la fricción basaí Esta solución (ecuación 5) es la ecuación de velocidad instantánea del flujo (EVEF) de material desagregado.
Si el esfuerzo debido a las fronteras laterales es insignificante en comparación con el esfuerzo en el lecho, la ecuación 5 describe el movimiento del centro de masa del cuerpo en deformación. Incluso si 0 varia como una fruición arbitraria de posición o el tiempo, la ecuación 5 se puede utilizar como una base para el cálculo por etapas del movimiento del centro de masa de las mezclas de Coulomb, ya sea con A constante o variable (Hutchmson, 1986). Integrando la ecuación de velocidad (5) se obtiene la ecuación de desplazamiento. Esta solución (ecuación 6) es la ecuación de desplazamiento instantáneo del flujo (EDIF) de material desagregado del centro de masa.
Los objetivos del análisis de sensibilidad son: 1) reconocer los parámetros de entrada que contribuyen más a la variabilidad de la salida, y 2) reconocer los parámetros que tiene la menor influencia sobre el modelo. Los valores que fueron utilizados para este análisis se encuentran dentro de los posibles rangos tanto a nivel experimental como real, que se muestran en la Tabla 2. Además en la Tabla 3 se presentan medidas precisas y también indirectas de velocidad y espesor de flujo de algunos casos reales de flujos de material desagregado.
Pasa evaluar el comportamiento de los modelos analíticos, se utilizan las condiciones iniciales como la velocidad, distancia y tiempo igual a cero, y todos los demás parámetros considerados por los modelos se suponen como constantes en el tiempo y en el espacio.
Lo que describe que una masa estática de volumen y geometría epecifica está a punto de descender una pendiente de inclinación constante.
Para iniciar es importante tener conocimiento del comportamiento general de la ecuación de velocidad instantánea del flujo (EVIF) (5). Por ejemplo, se puede identifica fácilmente que:
Lo que indica que la velocidad instantánea v _x (t) no aumenta de manera indefinida como en caída libre en el vacio, sino que, debido a la resistencia que ejerce el lecho en la base el flujo y a la viscosidad dinámica del componente fluido, tiende a una velocidad constante de manera asintótica. después de un tiempo determinado (figura 1). Por lo tanto, el flujo nunca se detiene principalmente como consecuencia de suponer que la pendiente de la trayectoria del flujo es constante, al igual que la fricción del lecho y la fracción de presión de poros.
Por otra parte el tiempo necesario para acercarse a una velocidad constante puede ser tan largo que es prácticamente inalcanzable porque las escalas de tiempo para la ecuación de velocidad instantánea del fluj o tiene valores de 106 s (~ 12 dias) cuando se introducen valores de los parámetro para que el fluio sea lo más rápido posible. Por ejemplo cuando p = 2400 kg/m3 z=9,81m/s,
Un análisis de sensibilidad de la EVIF se realiza tomando los diferentes valores que puede tener de espesor un flujo de material desagregado como se puede ver en la Figura 2. El espesor de flujos de material desagregado tiene un efecto importante sobre la velocidad del flujo, con valores de H inferiores a 1 m en tiempos cortos (<200s). Podrían ser flujos de pequeña escala o a nivel experimental Para flujos con valores de espesor iguales o superiores a 1 m (de gran escala) su influencia en la velocidad es baja para un tiempo < 200s, ya que la diferencia de velocidades es aproximada a 4,78 m's en flujos que tengan espesores entre 1 y 10 m.
Aunque para t>300s la diferencia de velocidades es mayor a 10 m s para flujos que tengan espesores entre 1 y 10 m, o cuando t—«o la diferencia de velocidades es ~3'6 m's para los mismos espesores, lo que hace que estos valores cobren importancia en la velocidad del flujo en tiempos prolongados. Esto se debe a que el espesor se encuentra en el numerador de la EVIF. Entonces, a mayor espesor de flujo mayor velocidad, y la ecuación 8 representada por la linea punteada en la figura 1 toma valores mucho más grandes si se toma a H>lm, lo que a su vez aumenta el tiempo de convergencia como se puede apreciar en la Figura 2.
La Figura 3 muestra la influencia de la viscosidad dinámica del componente fluido en la velocidad de la mezcla, a mayor viscosidad dinámica, menor velocidad. La velocidad puede diferir mucho para los posibles valores de viscosidades dinámicas en un fluido con sólidos suspendidos (arcillas y limos).
Según Montserrat, et al. (2005), mientras las partículas más grandes pueden ser las responsables de otorgar la inercia suficiente como para dar al finjo un carácter inercial, las fracciones más finas pueden alterar en forma dramática las propiedades Teológicas del fluido intersticial. Esta reologia de la mezcla agua-finos no solo depende de la concentración de finos, sino también de las características electroquímicas del material. Por otra parte, altos valores de viscosidad dificultan la resuspensión (ya que disminuyen los niveles de turbulencia) y reduce el grado de interacción entre partículas.
En la Figura 4a, se puede observar como la densidad de la mezcla del flujo de material desagregado afecta muy poco el resultado de la velocidad en un tiempo de 200s, ya que la diferencia es del orden de 2,4 m's si la densidad de la mezcla está entre los 1500 kg'in3 y 2400 kg'm3. Para t>300s la influencia de la densidad de la mezcla empieza a ser importante y aun más cuando t—wo, como se puede apreciar en la Figura 4a. La proporcionalidad de esta relación se puede decir que es: a mayor densidad mayor velocidad.
La explicación matemática de este comportamiento es que la densidad está en el numerador de la EVIF, de esta manera si la densidad aumenta también lo hará la velocidad. La explicación física, es que la densidad está siendo multiplicada por la gravedad, lo que se tendría con este producto es una fuerza unitaria. Asi, un flujo que tiene una masa m, mayor que un flujo de masa ni,, el flujo de ni será impulsado con mayor fuerza que el flujo de m,. Entonces a mayor masa, mayor fuerza, mayor velocidad y mayor aceleración.
La figura 4b, muestra la influencia de la fracción de volumen de fluido en la EVIF es un poco mayor que de la densidad de mezcla, aproximadamente 7.37 m's de diferencia, para un tiempo de 200s, si se tienen valores de fracción de volumen de fluido entre 0,3 a 0,7. Para t>200s la influencia de la densidad de la mezcla empieza a ser importante y aun más cuando t—«o, como se puede apreciar en la Figura 4b. Esta relación se puede decir que es inversa, a mayor fracción de volumen de fluido, menor velocidad.
Esto se debe a que la fracción de volumen de fluido esta directamente relacionada con la densidad promedio ponderada de la mezcla. Al aumentar la fracción de volumen de fluido (que es el componente de menor densidad), la fracción de volumen de sólidos disminuye de una fonna inversa (que es el componente de mayor densidad), y a su vez hace que la densidad de mezcla disminuya. Esta disminución de la densidad de la mezcla se ve reflejada en la disminución la velocidad del flujo como se ve en la Figura 4a.
También se analizó cual era la influencia del ángulo de talud 0, ángulo de fricción del lecho y fracción de presión de poros X. variables que hacen parte del parámetro 0 (ecuación 4). En este análisis de sensibilidad se encontró que si se ingresan al modelo valores dentro de los rangos posibles de estas variables, se tienen resultados de velocidad instantánea negativas a partir de un valor determinado. Este comportamiento del modelo se puede ver claramente en las figuras 5, 6 y 7, para ángulo de talud 0, ángulo de fricción del lecho tp^, y fracción de presión de poros X, respectivamente.
La Figura 5 muestra que a mayor ángulo de talud mayor velocidad. Para este caso especifico, con un ángulo de talud 0< a 16° la velocidad empieza a tener valores negativos. Según Suarez (1998), los movimientos tienden a comportarse como en caída libre cuando la pendiente superficial es mayor a 75°, en taludes de ángulo menor generalmente, los materiales rebotan y en los taludes de menos de 45° los materiales tienden a rodar.
La Figura 6 muestra que a menor ángulo de fricción del lecho mayor velocidad. Asi los materiales de fricción interna baja alcanzan los valores de velocidad más altas. Según (Baum, et al., 2003) los flujos de tierra más rápido se producen en zonas de depósitos de arcillas. Para este caso especifico, con un ángulo de fricción del lecho o_bed>44: la velocidad empieza a tener valores negativos.
En la Figura 7 se puede ver que a mayor fracción de presión de poros mayor velocidad. Aá, la máxima velocidad de acuerdo a este parámetro se alcanza cuando A = 1. Para este caso específico, con valores de fracción de presión de poros A < 0,2 la velocidad empieza a tener valores negativos. De estas observaciones se puede concluir que los parámetros de ángulo de talud (0), ángulo de fiicción del lecho (o^,) y fracción de presión de poros (A) son los que tiene mas influencia que los demás parámetros considerados por el modelo como la densidad de mezcla (p), el espesor de flujo (H), la viscosidad dinámica (p) y la fracción de volumen de fluido (nr).
De acuerdo con estas observaciones, se buscó el valor limite en el cual da como resultados valores positivos del parámetro 0 (sin tener en cuenta las otras variables de la EVIF). Este parámetro consecuentemente hace que el valor de la velocidad tenga el mismo signo (positivo). En el caso contrario en que el parámetro 0 de valores negativos, consecuentemente la velocidad tendrá valores negativos, que se pueden asociar a un estado estático del talud.
La búsqueda de esos valores limites están representados en la Figura 8, que refleja la importancia de la influencia del ángulo de talud, el ángulo de fricción y la fracción de presión de poros, ya que estos tres parámetros establecen si en el talud puede existir o no un movimiento. Si se ingresa en la Figura 8 con un ángulo de fricción entre los rangos posibles, cruzando con una linea de fracción de presión de poros, se puede detennmar cuales son los valores de ángulos de inclinación de tahid 0 en los que puede existir un movimiento. Por ejemplo, si se tiene un ángulo de fricción de 30° (Arena) y una fracción de presión de poros de 0,6; el ángulo de talud en el cual puede existir un flujo de material desagregado es 0>13,1° (linea punteada en la Figura 8), en el caso en que el ángulo de inclinación del talud sea <13,1° la posibilidad de que el talud presente inestabilidad disminuye
Con la ecuación de desplazamiento instantáneo del flujo (EDIF) (6) se puede conocer la posición del centro de masa de un flujo de material desagregado en un instante de tiempo detenninado. o si se despeja la ecuación se puede determinar cuanto tiempo tarda un flujo en recorrer una distancia cualquiera. En la Figura 9 muestra como se comporta la EDIF de matenal desagregado respecto al tiempo, y se puede apreciar que la posición x(t) tiende en foroia asintótica a la recta punteada cuando t-wo (ecuación 6).
El modelo de Iverson and Denlmger (2001) puede describir a aquellos tipos de movimientos en masa que estén compuestos por dos fases como: flujos hiper-concentrados, flujos de lodos, flujos de detritos, flujos de suelos y deslizamientos traslacionales, siempre y cuando se tenga presente que la presión de poros tana linealmente desde el un máximo en el fondo hasta cero en la superficie; y que se tienen esfuerzos cortantes por fricción entre sólidos.
El comportamiento general de la ecuación de velocidad instantánea del flujo (EVIF) de matenal desagregado tiende de manera asintótica a una velocidad constante, por lo que el flujo nunca se detiaie, principalmente como consecuencia de suponer que la pendiente de la trayectoria del flujo es constante, al igual que la fricción del lecho y la fracción de presión de poros.
Si el ángulo de talud, el ángulo de fricción del lecho y la fracción de presión de poros (dado como: 0 = tan 0 - (1-Z) tan <p bed) varían como una función arbitraria de la posición o el tiempo, la ecuación de velocidad instantánea del flujo (EVIF) y la ecuación de desplazamiento instantáneo del flujo (EDIF) se pueden utilizar como una base para el cálculo por etapas del movimiento del centro de masa del flujo de material desagregado.
Los parámetros que más influyen en la estabilidad de un talud haciendo uso de la EVIF son el ángulo de talud, el ángulo de fricción del lecho y la fracción de presión de poros.
El espesor de flujo influye de manera importante en la velocidad, ya que desde el inicio este parámetro hace que den diferentes resultados de velocidad.
La viscosidad dinámica del componente fluido influye significativamente en la velocidad, ya que con el aumento de la viscosidad, se desacelera el flujo considerablemente.
La ecuación de velocidad instantánea del flujo (EVIF) y la ecuación de desplazamiento instantáneo del flujo (EDIF) pueden ser utilizadas como insumo para evaluar el nesgo por flujos de material desagregado.
1. Baum. R_ L., Savage, W. Z. & Wasowski, J., 2003. Mechanics of Earth Flows. Sorrento, Italy, sn.. pp. 1-8.
2. Denlinger, R. P. & Iverson R M., 2001. Flow of Vanably Ruidized Granular Masses Across Three-Dimensional Terrain 2. Numerical Predictions and Experimental Test. Reviews of Geophysics, Volumen 106, pp. 553-566.
3. Frmini L. & Casagh, N., 2003. Prediction ofthe behaviour of landslides dam using a geomorphological dimensionless index. Earth Surface Processes and Landforms, Enero, 28(1), pp. 31-47.
4. Hutchinson J. N., 1986. A shdmg-consolidation model for flow slides. Canadian Geotechnical Journal, Mayo, 23(2), p.
115-126.
5. IDEAM. 2012. Instituto de hidrología, meteorología y estudios ambientales. [En linea] Available at http://www. pronosticosyaleTta5.gov.co''jsp;'loader.jsf?lServicio=Publicacione3&lTipo=pubhcacione3&lFuncion=loadContenidoPubl icacion&id=895 [Último acceso: 7 Marzo 2012],
6. Iverson, R. M., 1997. The physics of debris flows. Reviews of Geophysics, August, 35(3), pp. 245-296.
7. Iverson, R_ M., 2005. Debris-flow mechamos. En: Debris-flow hazards and related phenomena. Berlin Heidelberg: Springer Berlin Heidelberg, pp. 105-134.
8. Iverson, R. M. & Denhnger. R P., 2001a. Flow of variably fluidized granular masses across three-dimensional terrain 1. Coulomb mixture theory'. Journal of Geophysical Research, 10 January, 106(B 1), pp. 537-552.
9. Peralvarez, J. d., Chacón, J., El Hamdouni, J. & Irigaray, C., 2008. Análisis de susceptibilidad a los movimientos de ladera mediante un SIG en la cuenca vertiente al embalse de Rules. Granada. Madnd, s.n, pp. 15-27.
10. Pudasaim. S. P, Wang, Y. & Hutter, K, 2005. Modelling Debris Flows Down General Channels. Natural Hazards and Earth System Sciences, 26 Octubre, Volumen 5, pp. 799-819.
11. Quan Lima. B.y otros, 2012. Analysis of Debris Flows Behavior with a one Dimensional run-out Model Incoiporating Entrainment. Engineering Geology; 9 Marzo, Volumen 128, pp. 63-75.
12. Rickenmann. D., Laigle, D. M. B. W. & HhbL J., 2006. Comparison of 2D Debris-Flow Simulation Models with Field Events. Computational Geosciences. Marzo, 10(2), pp. 241-264.
13. Shrestha, B. B_ Nakagawa, H.. Kawaíke, K. & Baba, Y., 2008. Numerical simulation on debris-flow deposition and erosion processes upstream of a check dam with experimental verification. Annual of Disas. Prev. Res. Inst., Issue 51B, pp. 613-623.
14. Suarez, J., 1998. Deslizaminetos y estabilidad de taludes en zonas tropicales. Bucaramanga(Santader): Universidad Industrial de Santander.
15. Vargas, R. A., 2000. Seminario estudios de nesgos por fenómenos de remoción en masa. Bogotá D.C.(Cundinamarca): Dirección de Prevención y Atención de Emergencias de Santa Fe De Bogotá.
16. Villacorta. S. y otros, 2007. Análisis de la suceptibilidad a los movimientos de ladera en la cuenca del río Llammchán (Cajamarca, Peni). Revista del Instituto de Investigaciones FIGMMG,10(19), pp. 103-112.
17. Wang, C., Li, S. & Esaki, T, 2008. GIS-Based Two-Dimensional Numencal Simulation of Rainfall-Induced Debris Flow. Natural Hazards and Earth System Sciences, 4 Febrero, Volumen 8, pp. 47-58.