Jesús Salgado Patrón1, Mayra Alejandra Peralta2 y Luis Camilo Gómez T3
Este trabajo presenta una alternativa de identificación y predicción, cualitativa y cuantitativa, de los problemas en el equipo de subsuelo de sistemas de bombeo mecánico, reflejados en los dmagramas de fondo para establecer una metodología en análisis de la información de 512 dinagramas de 8 pozos de la región norte del departamento del Huila, proporcionada por ECOPETROL Luego de hacer una recolección y clasificación manual de los dinagramas, y de formar una base de datos, se identificó si el problema era adecuado para ser resuelto por medio de redes neuronales. Postaioimente se aclara el procedimiento para extraer las características más significativas de cada dinagrama por medio de un método de procesamiento de señales llamado Transformada Wavelet.
Se diseñó y probó distintos algoritmos de la transformada para obtener los coirespondientes coeficientes de aproximaciones y detalles de las señales, para luego aplicarlos al entrenamiento de una red neuronal de mapas auto organizados (Self Organazing Maps SOM), capaz de realizar su inteipretación de una forma más rápida y asertiva. Los resultados de la investigación se adaptaron a un software final que suministra además de identificación, predicción de manera ágil y precisa a los problemas en los equipos de bombeo mecánico con el fin de minimizar los costos de operación y maximizar la producción en la industria.
Palabras clave: SOM: wavelet; bombeo mecánico; dinagrama; redes neuronales
This paper presents an alternative for identification and prediction, qualitative and quantitative, of the problems in the equipment subsoil system rod pumping, reflected in the downhole dynamometer charts to establish a methodology' for data analysis of 512 dynamometer charts of 8 wells the northern region of Huila. provided by Ecopetrol. After making a collection and manual classification of dynamometer charts, and to form a database, if the problem identified was suitable to be solved by neural network. Subsequently clarifying the method for extracting the most significant characteristics of each dinagrama by a signal processing method called Wavelet Transform.
Was designed and tested different algorithms transform to the corresponding coefficients of approximations and details of the signals, and then apply them to the training of a neural network of self-organizing maps (SOM), capable of performing his own interpretation was faster and more assertive. The research results were adjusted to final software also provides identification, prediction swiftly and accurately to problems m mechanical pumping equipment in order to minimize operating costs and maximize production m the industry.
Keywords: SOM; wavelet; mechanical pumping; dinagrama; neural networks.
La industria del petróleo cada día busca optimizar sus métodos tanto para la exploración, explotación como para la producción de petróleo (Svinos, 1998). Es así, como las empresas encargadas de este medio tratan de encontrar técnicas Neuro-computacionales que les garanticen de forma eficiente y óptima buenos resultados, contrano, a lo que las técnicas antiguas o convencionales ofrecen.
En la actualidad hay muchos estudios en distintas áreas de la Neuro-computación, acerca de la forma de aplicar las redes neuronales a las tareas dianas éste es el caso de las industrias, que han retomado ostensiblemente tales técnicas (redes nemorales), debido al aumento de la capacidad de procesamiento de las máquinas y la posibilidad de poder aplicar este método de análisis a tareas dispendiosas, realizadas por personas expertas.
La producción promedio de crudo actualmente en Colombia se ubicó en 955.000 barriles por dia (bpd), es decir un 5,4% más frente a los 906.000 barriles que se registraron en abril de 2011. Por esta razón Colombia está ubicada en la posición 25 de los paises productores de petróleo. Gran parte de esta producción proviene de pozos que utilizan el bombeo mecánico como su método de levantamiento artificial debido a que es el más económico y más fácil de mantener cuando es diseñado y operado apropiadamente. Es asi como en Colombia, la Universidad Industrial de Santander (UIS), con su Grano de Investigación en Exploración y Explotación de Hidrocarburos, poseen varios estudios de este tipo de aplicación de redes neuronales.
En el Huila, en la Universidad Surcolombiana está naciendo el interés de desarrollar proyectos basados en las técnicas de Neuro-computación (redes nemorales), pero no existen grupos de investigación que propicien el desarrollo más acelerado de este tema. Por eso, esta investigación se ha interesado en continuar el trabajo iniciado por el ingeniero Leonardo Franco y el Ingeniero Carlos Pérez, con el fin de que sirva de inspiración para los que quieran continuar con el desarrollo en el campo de las redes neuronales y la aplicación de técnicas de procesamiento de señales, y con ello ampliar el conocimiento y mejorar la calidad de la investigación en la universidad.
La supervisión del bombeo mecánico produce un gran flujo de datos e información (dinagramas. perfiles de exploración, etc.) que necesita ser analizado e interpretado. En muchos casos el análisis de toda esta información se hace de forma manual y ésto se toma tedioso, lento y agotador para los ingenieros expertos, por tanto es necesario desarrollar herramientas expertas para el análisis automático aplicado a la detección, predicción de problemas que permitan tomar de forma rápida decisiones acertadas y eficientes para la solución de los mismos.
Motivados por los nuevos adelantos de anáfisis de señales, como la Transformada de Wavelet (TW) y redes de clasificación autorganizados, SOM, que han demostrado ser una herramienta muy poderosa en Minería de Hiatos (Data Mining) y en metodología de Descubrimiento de Conocimiento en Base de Datos (Knowledge Discovery Database (KDD)) y con una gran variedad de aplicaciones de ingeniería tales como reconocimiento de patrones, análisis de imágenes, monitoreo de procesos y detección de fallas por nombrar algunas, el software DinaSOM. busca aplicar estos conceptos para el anáfisis e identificación de la información representada en cartas dinagráficas. además se desarrolló una herramienta experta que permite optimizar unidades de bombeo mecánico de forma más apropiada.
Para el trabajo propuesto se desarrolló un software experto para la optimización de unidades de bombeo mecánico, agregando descripciones de comportamientos el cual contiene: anáfisis de registros históricos, el estudio de trayectorias de fallas asociadas y el monitoreo de múltiples pozos presentándolos por medio de una interfaz gráfica tipo radar, con múltiples sub-pantallas para que se puedan realizar distintos tipos de observaciones sobre el comportamiento de las fallas.
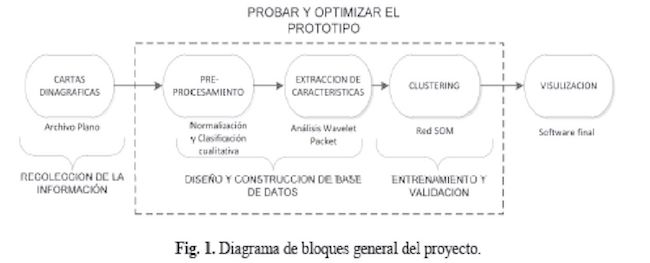
El diagrama de bloques general que se observa en la Figura 1., inspiró la producción del algoritmo aplicado al software, donde se describen cuatro etapas principales, presentes en cualquier proyecto Neuro-computacional: Recolección de la información. Diseño y construcción de la base de datos, Entrenamiento y validación de la red neuronal y visualization o Software final. A lo largo de las etapas centrales también se prueba y optimiza el prototipo diseñado.
El siguiente diagrama (Figura 2), ilustra claramente y de fonna detallada cada una de las etapas descñtas en el diagrama de bloques anterior. Basados en este esquema se procedió a realizar el desarrollo del trabajo.
En la etapa 1 los registros de los diferentes dinagramas provenientes del ECHOME I EK (ECHOME IEK, 2006), se han guardado en un archivo plano pasando a la etapa 2 donde se clasificaron de forma manual para saber qué clase de información se tenia del proyecto. Luego se analizaron a través de procesamiento digital de señales (DSP por sus siglas en inglés) para luego seguir con la etapa 3 en la cual se procedió con la construcción del software, donde a la base de datos de los dmagramas ya pre procesados se le aplicó la transformada wavelet, debido a que estas señales son de naturaleza no estacionarias siendo esta una poderosa herramienta para este trabajo, y finalmente en la etapa 4 se construye la red SOM y la visualización de los resultados por medio de un software adaptado a las necesidades de la industria.
En el caso de diagnóstico de problemas si el equipo de subsuelo de unidades de bombeo mecánico las técnicas tradicionales hablan concretamente de la interpretación y análisis de dmagramas. Esta tarea se basó en la identificación de formas o comportamientos que han sido preestablecidos para determinar los problemas y dependiendo de si estas formas patrón estaban implícitas en el dmagrama de fondo o no, el equipo de subsuelo presentaba el problema relacionado con dicha forma patrón o se encontraba funcionando nonnalmenie.
De esta forma se describe el problema en una tarea de reconocimiento de patrones y clasificación de dmagramas con base en un conjunto de datos, ejercicio que se desarrolló por medio de la red SOM como herramienta.
El proceso de entrenamiento y ajuste de la red SOM file posible cuando se realizó el análisis de los patrones de entrenamiento, para asegurar un reconocimiento e identificación de problemas con un error minino. Por lo tanto el esfuerzo más grande se debió concaitrar en construir una base de datos de entrenamiento con ejemplos óptimos en cuanto a definición de los problemas y extraer cada uno de los problemas más relevantes que caracterizaban cada situación. Además es fundamental en este tipo de proyectos la utilización de una topología adecuada de las SOM y una cantidad de neuronas mayor a los patrones detectados, que en el caso del proyecto son las clases, para que no existiera ambigüedad y que permita cumplir los objetivos propuestos (reconocimiento, clasificación y predicción de los datos del dinagrama de entrada a la red).
La información la proporcionó la empresa Ecopetrol con base en pruebas tomadas a algunos pozos cercanos a la ciudad de Neiva. estos pozos se encuentran ubicados en los campos Bnsas. Cebú y Santa clara.
Los datos del dinagrama de fondo del pozo que fueron analizados son coordenadas tipo (x,y), que corresponden a las coordenadas de posición del pistón y caiga soportada por la primera sarilla después de la bomba, respectivamente. Los datos fueron extraídos del software TWM (Total Well Management) Echometer y guardados separadamente en archivos planos (tipo XLS) para su posterior pie-procesamiento índmdual y pre-clasificación.
En esta etapa se estableció y organizó la información necesaria sobre cada dinagrama. De esta forma se realizó un pre-procesamiento. que consiste en una clasificación cualitativa de los pozos y una normalización, seguido de la codificación de los datos para el entrenamiento por medio de la TW.
Ya que no todos los pozos son iguales, se requirió de diferentes herramientas para diagnosticar problemas dependiendo de las condiciones del pozo. Se dividió entonces los pozos con bombeo mecánico en dos grupos. El primer grupo recibió el nombre de “grupo 1”, incluye pozos mayores de 4000 ft de profundidad con cualquier tamaño de pistón, y pozos con menos de 4000 ft y pistones de 2 m o menos. El segundo grupo, al cual se llamó “grupo 2”, incluye pozos con menos de 4000 ft y con pistón mayores de 2.00 m. Estos dos grupos de pozos poseen características únicas que se debe conocer para diagnosticar problemas con precisión.
La razón para separar los pozos someros de alta producción del grupo 2 de los pozos profundos (grupo 1) es porque los mismos son afectados por las fuerzas de inercia de los fluidos, que con frecuencia duplican la carga sobre el pistón. Debido a que los pistones en estos pozos son grandes, éstos deben recoger el fluido y acelerarlo a la tubería en tazas mucho mayores que en pozos más profundos. Además la sarta de cabillas está rígida y no provee ningún nivel de amortiguación.
En pozos del grupo 1, para reducir la caiga de la sarta de cabillas se debe usar un pistón de poco diámetro. La sarta de cabillas actúa como un amortiguador estirándose al aumentar la carga en el pistón; ésto absorbe efectivamente el “golpe" de recibir la caiga de fluido en la carrera ascendente y no aparecen fuerzas de dinámica de fluido en la caita dinagráfica de fondo. Por lo tanto, sólo en pozos del Grupo 1 la condición de la bomba se puede identificar por la comparación con fomias conocidas de cartas dinagráficas.
Una vez se organizaron los dmagramas en los dos tipos de pozos, se clasificaron manualmente teniendo en cuenta la fonna aparente del dmagrama. Ésto se hizo con el fin de reconocer a pnon las fallas o patrones dominantes que podrían llegar a poseer los pozos.
Como se conoce, un dmagrama está representado por impar de vectores columnas (x e y). Pero al tener datos reales se descubre que cada dinagrama posee diferaites longitudes y diferentes tazas de muestreo, por lo que es indispensable su normalización. Este proceso consiste en agrupar los valores en el rango entre cero y uno en cada eje coordenado, lo que permite estandarizar los datos para que trabajen a una misma escala y así se puedan correlacionar más fácilmente para un mejor reconocimiento en la red neuronal.
La ecuación 1 empleada para este fin es la siguiente:
Una vez se normalizaron los datos de cada dinagrama se igualaron sus dimensiones para finalmente compilar la información en una gran matriz M_180xl038. Esta matriz se obtiene de agrupar un total de 519 dinagramas. donde cada dinagrama contiene 180 datos que son obtenidos dependiendo del tiempo de muestreo de la señal tomada físicamente en el pozo.
Para la extracción de características por medio de TU' se seleccionó sólo la información de carga de cada dinagrama quedando reducida la matriz a un tamaño de 180X519. Sus respectivas gráficas en 2D y 3D se muestran en las Figuras 3 y 4.
Se optó por hacer un análisis multnresolución (Hernández. 2003) mediante wavelet packet debido a la naturaleza no estacionaria de las señales (Misiti et al., 1997), se seleccionó primero la wavelet madre que mejor se adapte a cada diagrama, luego un nivel óptimo de descomposición y posteriormente la mejor base (Best Basis), que contiene los nodos con la información más predominante de la señal.
A partir de un conjunto de 17 wavelet básicas que comprenden las familias Daubechies, Biorihogonal, Reverse Biorthogonal y Coiflets con sus respetivas órdenes, se realizó la selección de la wavelet madre en base a un criterio de información (Bemal et al., 2009).
Se calculó la función de costo de información basada en la Entropía de Shannon (Orozco, 2005) para cada señal de dinagrama con cada wavelet base del conjunto preestablecido, de tal manera, que la selección final de la wavelet madre recayó sobre la ftmción que tuviera el menor valor.
De lo anterior se encontró que para el 98% del total de las señales, la wavelet madre seleccionada fue la Daubechies de orden 25 (db25), debido a que es la wavelet que más momentos de desvanecimiento posee, o sea, con mayor capacidad para representar el comportamiento polmonnal de la señal.
Después de que se escogió la wavelet madre se tuvo en cuenta un número adecuado de niveles de descomposición basados en la naturaleza de la señal y se buscó una reducción significativa en la longitud del vector de coeficientes que caracterizan el dmagrama sm sacrificar la información que éste contenía.
En este sentido, la idea fundamental consistió en relacionar la longitud del vector de los coeficientes del anáfisis wavelet packet y el error de aproximación a la señal original de manera que el nivel óptimo de descomposición conserve la relación más equitativa. (Tabla 1).
Este análisis se hizo para 60 dinagramas en general con resultados mostrados en el Tabla 2. En el 80% de los casos el nivel más óptimo fue el 4 y en el 20% restante fue el nivel 5.
El árbol binario de cuatro niveles que resultó del análisis wavelet packet permite 24 diferentes caminos para codificar la señal. Escoger la descomposición más adecuada significa analizar cada nodo del árbol y cuantificar la información que se puede obtener de la realización de cada división mediante el algoritmo de análisis de entropía.
Finalmente, se obtuvo un nuevo vector de coeficientes de aproximaciones y detalles de 114 elementos por cada dinagrama que se proporcionó a la red SOM para su postenor clasificación.
La SOM por ser una red neuronal de clasificación no supervisada, también conocida como técnica de clustering, no necesita conocer de antemano la pertenencia de cada dato de entrenamiento a un grupo preestablecido para realizar los agrupamientos. Sin embargo, como se disponía de esa información, se utilizó posteriormente para evaluar la calidad de los clusters y para “etiquetarlos” (poner nombre).
El éxito de las redes SOM se debe a su propiedad especial de crear de forma efectiva representaciones internas espacialmente organizadas de varias características de las señales de entrada y sus abstracciones (Kohonen, 1990).
El siguiente paso luego de que se obtuvieron los dinagramas en el formato deseado para la entrada de la red SOM, fue realizar el entrenamiento. En este punto se le proporcionó además de los datos, las características de la red a entrenar como son: la topología (posiciones físicas de las neuronas), función de distancia, útil para calcular la distancia entre las neuronas, distancia inicial de vecindario y tamaño del mapa de salida.
La topología de la red puede ser rectangular, hexagonal o aleatona, y las funciones de distancia existentes son: distancia euclidiana, distancia cuadrada (boxdist), distancia de pasos (linkdist) y distancia manhattan (Beale et al., 2012).
Aunque la evaluación o validación sobre esta red no tendría ningún impacto en la formación de la función de entrenamiento por ser no supervisada, si puede servir como medidas independientes de generalización de la red.
La evaluación se realizó teniendo en cuenta la respuesta a los patrones de prueba constituidos por dinagramas diferentes a los del entrenamiento, si la evaluación de la red arroja resultados buenos en cuanto al reconocimiento de uno y dos problemas, entonces se termina el proceso de evaluación de la red, si es el caso contrano es necesario modificar la estructura de la red y volver a realizar el proceso.
El prototipo se convirtió en el modelo oprimo cuando el sistema fue confiable, es decn que produzca las soluciones requeridas en la fase de prueba. Para cubnr este aspecto se debió ejecutar diferentes pruebas entre las cuales se evaluaron las entradas de la red, el tamaño de los mapas de salida (número de neuronas) y las diferentes topologías en cada caso.
Cuantificar la eficiencia de una SOM no es una tarea fácil. puesto que no hay un objetivo claramente especificado en el entrenamiento al cual se tenga que adaptar la red para asi poder determinar un error. Sin embargo, en este trabajo se infirieron los siguientes dos métodos que proporcionan alguna medida del comportamiento de la SOM:
a) Distancia del vector de entrada y su neurona ganadora.
Con este método se intentó medir que tanto se ajusta la red a la topología del conjunto de entrada, calculando el promedio de las distancias entre los vectores de entrada (r,) y sus correspondientes neuronas ganadoras (/). Siendo iVel número de vectores o muestras de entrada, y m el vector de pesos de la neurona ganadora para el vector de entrada x, este promedio se define en la ecuación 2 como:
Luego se encontró en la literatura que este promedio es llamado error de cuantización(Arsuaga et al,. 2005).
b) Error Topográfico de Kiviluoto. Aparte de estudiar la precisión con que las neuronas se adaptan a la topología de entrada, se hace necesario evaluar que tanto conservan las redes sus diferentes topologías iniciales basados en el error topográfico propuesto por Kiviluoto en la ecuación (3) (Kiviluoto, 1996):
Donde, N: número de muestras, x: la muestra i-ésima del conjunto de datos, i/(x): valor en función de la posición relativa entre las dos principales neuronas ganadoras de las muestras x en el espacio de salida.
u(κ)= 1 Si las dos principales neuronas ganadoras no son adyacentes. 0 Si son adyacentes
De este modo el menor error significa que conserva su topología original. Se observó que en la mayoría de los casos, el promedio de distancia (o error de cuantización) decreció conforme el tamaño del mapa aumenta. Esto es lógico pues como el número de neuronas aumenta, hay más neuronas para representar los datos y cada vector estar más cerca de su neurona ganadora. Pero este criterio fue suficiente para determinar cuál era el tamaño del mapa y la topología más adecuada. Había que fijarse entonces que tanto conservan esas redes su topología. El error topográfico no demostraba una tendencia aparente, lo más notono era que las redes aleatorias poseen los errores más altos, tal vez porque no tenían una distribución definida y era difícil evaluar si ésta se conserva.
Para efectos prácticos en este trabajo se optimizó la red a una con topología hexagonal de 60 unidades, pues presentó el menor error topográfico, y la distancia promedio de la neurona ganadora también es una de las más bajas.
En esta sección se presentan los resultados del entrenamiento y la simulación de la red neuronal con toda la base de datos conformada y se presenta la visualización de estos resultados mediante un software final.
En la Figura 5 se muestra la topología inicial donde las neuronas se distribuyen de forma equidistante en un mapa de dos dimensiones. Por lo tanto, es posible visualizar un espacio de entrada de alta dimensión en las dos dimensiones de la topología de la red.
En esta figura, cada punto rojo es una neurona y las lineas azules, la forma en cómo se interconectan. Las dimensiones son 10x6, asi que hay un total de 60 neuronas.
Finalizado el entrenamiento, las neuronas lian cambiado sus distancias entre ellas de acuerdo con los clusters presentes en los datos de entrada. Esta información se conoce como matriz de distancia de los vectores de pesos de las neuronas o matriz U, y se puede observar en la Figura 6.
Los hexágonos azules representan las neuronas. Los colores en las regiones que contienen las lineas rojas indican las distancias entre las neuronas, mientras más oscuro es el color mayor es la distancia.
Las neuronas en la mayor parte del mapa poseen las menores distancias entre ellas, esto se puede atribuir a que haya una mayor densidad de datos en esta zona y por ende se requiera más neuronas para su clasificación. Por otra parte, hay 5 o 6 neuronas muy separadas del resto del conjunto, útiles para representar fallas atipicas o información diversa.
En la Figura 7, se muestra cómo la SOM clasifica el espacio de entrada, mostrando puntos de color azul gnsáceo por vector de pesos de cada neurona y la conexión de las neuronas vecinas con lineas rojas. Los vectores de entrada están dibujados como puntos verdes.
Hay que advertir que la Figura 7, solo proyecta 2 de los 114 valores que posee cada vector de pesos. La máxima visualización que se puede obtener es en tres dimensiones, y se muestra en la Figura 8.
La Figura 9 indica cuantos de los datos de entrenamiento están asociados a cada neurona. El máximo número de muestras con alguna neurona es 22.
Las trayectorias se utilizan principalmente para predicción, pues muestran la tendencia de las fallas próximas a ocurrir a lo largo de los eventos. Cada trayectoria se obtiene a partir de las distancias ascendentes, desde la neurona ganadora hasta la décima neurona.
Se inició con la gráfica de todas las trayectorias posibles para cada una de las clases obtenidas. Luego se estudió cual es la clase más frecuente para cada uno de los eventos calculando su porcentaje de ocurrencia, para finalmente establecer una sola trayectoria que muestre la predicción más adecuada.
El software DinaSOM usa una red SOM entrenada para la optimización de unidades de bombeo mecánico. Se diseñó lina interfaz gráfica en donde el operano puede encontrar descripciones de comportamientos como: análisis de registros históricos, el estudio de trayectorias de fallas asociadas y el monitoreo por medio de tina interfez gráfica tipo radar. Esta interfaz permite relacionar formas de dinagramas con los nombres de las fallas brindándole al usuario una base de conocimiento rápida y acertada para realizar la interpretación de dinagramas, agilizando la identificación de problemas en los sistemas de bombeo mejorando el tiempo de respuesta en caso de una contingencia.
El software DinaSOM se destaca porque además de ser tura herramienta de identificación y anáfisis muestra las tendencias de las fellas en forma de trayectorias, permitiendo tener un panorama general de la situación futura del pozo ya que no solo identifica la falla en el momento sino que muestra una serie de fallas cercanas en formas de trayectoria, con las cuales se puede prevenir un daño que saque totalmente de funcionamiento el pozo.
Por ser un software basado en una red de entrenamiento no supervisada su validación es más complej a, porque no existe una función especifica para evaluar el performance de esta red neuronal.
Se realizaron 70 pruebas para poder hacer la validación del programa y asi observar el éxito del clasificador. Los resultados se muestran en el Cuadro 3 y la Figura 13.
Se observa que el 85,71% del total de los casos evaluados fueron exitosos frente a un 14,28% que fueron confusos o no acertados. La ocurrencia de estos casos erróneos se debe principalmente al dinagrama escogido para la visualization de cada falla, es decn que el dinagrama representativo de cada neurona, en pocos casos, no fríe el más adecuado. Se corrobora esta afirmación con los valores de los porcentajes promedios de asertividad de las neuronas ganadoras; en las dos opciones este valor fue superior al 90%. esto quiere decir que la neurona ganadora en cada caso se aproxima bastante bien a los datos de entrada. Cabe destacar que cuando la identificación es positiva la neurona sanadora tiene un porcentaje de acierto por encima del 92%.
La visualización de cada falla, es decir que el dinagrama representativo de cada neurona, en pocos casos, no fue el más adecuado. Se corrobora esta afirmación con los valores de los porcentajes promedios de asertividad de las neuronas ganadoras; en las dos opciones este valor fríe superior al 90%, esto quiere decu que la neurona ganadora en cada caso se aproxima bastante bien a los datos de entrada. Cabe destacar que cuando la identificación es positiva la neurona ganadora tiene un porcentaje de acierto por enama del 92%.
Fue diseñada con Matlab utilizando el GUIDE como se observa en la Figura 14. Esta interfaz es de manejo fácil y puede ser ejecutada por cualquier persona con o sin conocimientos de Matlab.
DinaSOM cuenta con dos posibilidades para el ingreso de datos, estos datos deben estar en formato (.xls) o extensión (csv) en forma de tabla con dos columnas con datos mayores de 180 filas.
La primera columna debe contener los datos correspondientes a la carga de los dmagramas y la segunda columna corresponde a los datos del desplazamiento tomados por el dinamómetro de la bomba y al final lo que se le ingresa al software DinaSOM en una matnz de dos columnas por 180 o más filas.
En la pantalla principal, en el Toolbar, se le da clic izquierdo al icono universal de Abrir. Al seleccionar Abrir se muestra otro sub-menu como se ve la Figura 14. Luego se busca, se selecciona y se abre el dinagrama que se desea cargar.
Después de que el archivo ha sido cargado al programa, se le da clic en el botón “Identificar falla” y se tendrá un resultado como la Figura 14.
El dinagrama que se ha cargado presamente se muestra en el panel “Dinagrama ingresado”, y en el panel “Identificador” se muestra la falla a la cual ha sido asociado.
También posee un panel de “Diagnóstico” donde se visualiza una breve descripción de la falla asignada por el diseñador para una mejor identificación del problema, ésto pensando en la posibilidad de identificar de forma más rápida la falla para que el experto formule las correcciones de los daños en los equipos de fonna más ágil.
Y el panel “Radar”, que apoya el proceso de identificación, puede seguir el comportamiento del pozo a medida que se van identificando las fallas y ésto da la posibilidad de tener una gráfica del estado de las fellas de la bomba y cuál seria su tendencia.
La red neuronal SOM que contiene el identrficador toma las características de la carta dinagráfica ingresada y selecciona la falla que más acerca a esas características. Esta buena asociación de patrones es producto del entrenamiento y la robustez con la que cuentan las redes SOM sin importar que el dmagrama de entrada nunca haya sido procesado en el entrenamiento déla red neuronal.
En la casilla con el nombre de: porcentaje de acierto, ubicada bajo el panel de diagnóstico, se visualiza porcentaje de semejanza del dmagrama ingresado y el dinagrama identificado por el software.
Esta opción se implemento como herramienta para visualizar las trayectorias de las posibles futuras fallas más cercanas al dinagrama de entrada y evaluar su grado de certeza, mejorando de esta forma la confianza a la hora de tomar decisiones para ejecutar trabajos en los equipos de fondo.
Al presionar el botón “Predecir comportamiento” corno se muestra en la Figura 15, el programa calcula la trayectoria de las posibles fellas más próximas a ocurrir.
La gráfica muestra la trayectoria de las posibles fallas futuras sino se realiza un mantenimiento a tiempo de la bomba. Cada punto de la trayectoria hace referencia a la falla más próxima en cada evento por ocurrir.
El desarrollo de esta aplicación inteligente y además efectiva, requiere conocimientos previos de interpretación de dmagramas, métodos para realizar procesamiento de señales y aplicación de redes neuronales artificiales SOM, debido a que si existen falencias de conocimientos en estos campos se hace muy laborioso desarrollar un algoritmo para la identificación de problemas en los equipos de subsuelo de las unidades de bombeo mecánico de manera exitosa.
El hecho de igualar las dimensiones de todos los vectores de entrada de los dmagramas para su entrenamiento, hace que se pierda cierta información de la señal que puede ser relevante en el momento de la clasificación.
Las redes SOM crean mapas autoorganizados para clasificar muestras con tanto detalle como se desee, seleccionando el número de neuronas en cada dimensión del mapa de salida. Así proyectan datos de entradas de altas dimensiones en bajas dimensiones respetando la densidad espacial de los datos.
Después de probar varios métodos de procesamiento para la extracción de características relevantes de los dmagramas, se encontró que el más adecuado para este tipo de señales, que tienen una frecuencia de muestreo variable o dinámica, es la Transformada Wavelet; debido a que este método utiliza un algoritmo matemático que se adapta a esa variación de la señal y proporciona diferentes resoluciones de tiempo y frecuencia.
La información obtenida de la transformada wavelet viene discriminada en fonna de niveles, donde cada nivel contiene coeficientes de aproximaciones y detalles, formando un árbol jerárquico. Esto quiere decir, que luego de analizar una señal existen diversas rutas o caminos que contienen nodos con la información de descomposición más notable de la señal.
Las redes neuronales artificiales (SOM) presentaron un mejor reconocimiento al involucrar en su etapa de aprendizaje dmagramas con fallas combinadas, acorde a los problemas reales presentes en los pozos.
En las redes SOM, debido a la ausencia capas ocultas yporposeerun algoritmo no supervisado, el tiempo de entrenamiento toma de 6 a 10 segundos. Tiempo considerablemente bajo comparado con el de otras redes de carácter supervisado.
1. Arsuaga U., Diaz M., 2005. Topology Preservation in SOM. International Journal of Mathematical and Computer Sciences, p. 19.
2. Beale, M., Demuth. H., Hagan, M, The Matworks, 2012. Neural Network Toolbox User's Guide. Self-Organizing and Learning Vector Quantization Nets. p. 6.2-6.47.
3. Bemal, H. Rodríguez, A. 2009. Identificación de zonas productoras de hidrocarburos aplicando DSP y métodos de correlación de registro de perfilaje. Trabajo de grado Ingeniero Electrónico. Neiva. Tesis de grado. Universidad Surcolombiana. Facultad de Ingeniería, 55 p.
4. ECHOMETER COMPANY, 2006. Well Analyzer and TWM Software Operation Manual, REV C. Consultado el 15 de septiembre de 2012. httph'www.echonieter.com'supporimanuals.
5. Hernández, M., 2003. Análisis Comparativo de Algoritmos para Reducción de Ruido en Señales Utilizando Wavelets. Cholula. Puebla, México. Tesis de grado. Universidad de las Americas Puebla. Escuela de ingeniería. Departamento de Ingeniería Electrónica
6. Kivihioto, K., 1996. Topology preservation m self-organizing maps. Proceedings of the IEEE International Conference on Neural Networks, 249-299.
7. Kohonen, T., 1990. The Self-Organizing Map. Proceedings of IEEE, vol. 78, no. 9, p. 1464-1480.
8. Misiti, M., The Math Works, 1997. Wavelet Toolbox for use with MATLAB. 626 p.
9. Orozco, M. 2005. Selección efectiva de características wavelet en la identificación de bioseñales 1-D y 2-D usando algoritmos genéticos. Manizales. Tesis de grado. Universidad Nacional de Colombia. Ingeniería eléctrica, electrónica y computación.
10. Sainos, J. G., 1998. Optimización de bombeo mecánico. Theta Enterprise, Inc. 292 p.