|
|
|
|
Freddy H. Escobar M.1, John Francisco Carvajal2 y Edinson Cortés C.3
Resumen
En este artículo se presenta el proceso de diseño de un algoritmo para deconvolver la derivada de presión, el cual elimina el efecto de almacenamiento e indica el comportamiento del flujo radial. El diseño está basado en el método de deconvolución iterativo propuesto por Jansson (1984). En la validación del algoritmo, se ha encontrado que funciona bien en conjuntos consistentes de datos de presión contra tiempo. Sin embargo, se produce un error, cuando se utiliza con datos inconsistentes. Un cierto grado de incompatibilidad normalmente está presente en los datos de prueba real.
Palabras Clave: deconvolución; algoritmo; presión; almacenamiento; flujo radial.
Abstract
This article presents the process of designing an algorithm for deconvolved pressure derivative, which eliminates the effect of storage and indicates the radial flow behavior. The design is based on iterative deconvolution method proposed by Jansson (1984). In the validation of the algorithm, we have found that works even on data sets consisting of pressure versus time. However, there is an error, when used with inconsistent data. Acertain degree of inconsistency is normally present in real test data.
Keywords: deconvolution; algorithm; pressure; storage; radial flow.
1. Introducción
Desde 1930 muchos investigadores se han dedicado a buscar métodos iterativos que den solución al problema de la deconvolución, uno de los pioneros dentro de este método es sin duda Van Cittert (Van C, 1931). Quien propuso un método lineal para la deconvolución de señales, el cual es base fundamental de toda una serie de métodos iterativos entre los cuales se encuentra el método de deconvolución iterativa de Jannson (Jansson P, 1984).
La deconvolución del cambio de la presión es un gran problema del análisis delas pruebas de pozos que ha sido objeto de investigación de muchos autores. Una variedad de diferentes algoritmos de deconvolución han sido propuestos en la literatura, sin embargo ninguno de estos es lo suficientemente robusto como para ser implementado en un software comercial del análisis de pruebas de pozos altamente usado en la industria. En la actualidad el uso de las pruebas de pozos se ha hecho más necesario debido al uso de un nuevo algoritmo para la deconvolución desarrollado por Shroeter (von Shroeter T, 2001). El cual ha demostrado trabajar bien cuando un nivel razonable de ruido está presente en los datos de caudal y presión.
El comportamiento de la presión de fondo o de pozo en respuesta a una prueba de flujo constante es una función de respuesta característica del sistema en el pozo. La respuesta depresión transitoria a velocidad de flujo constante depende de la reserva y propiedades del pozo como permeabilidad, heterogeneidades a gran escala y el factor de daño. También depende de la geometría del flujo del depósito definido por la geometría de la terminación del pozo y por los límites del yacimiento. Por lo tanto, estas reservas y características del yacimiento son reflejadas por la respuesta de los sistemas para declinación de la presión transitoria a tasa de flujo constante, y muchas de estas reservas y características del pozo pueden ser potencialmente recuperadas de la función de respuesta por medio de métodos convencionales de análisis de pruebas de pozos.
La medición directa de la respuesta de presión transitoria aflujo constante no suele producir datos de buena calidad debido a nuestra incapacidad para controlar con precisión las variaciones y porque la presión es muy sensible a la variación de la tasa de flujo. Por esta razón, las pruebas de pozo típicas no son a tasa de flujo constante sino variable. Una secuencia de pruebas de pozos normalmente incluye varios períodos de flujo. Durante uno o varios de estos períodos de flujo, el pozo es cerrado. Después solamente los datos de presión adquiridos durante un periodo de cierre tienen la calidad requerida para el análisis de presión transitoria. El comportamiento de la presión durante un período de flujo individual de una secuencia de prueba multiflujo depende de la historia del flujo anterior antes que de dicho periodo de flujo. Por lo tanto, la función de respuesta no es igual a la función para una tasa de flujo constante. La teoría de análisis de pruebas de pozos desarrollada en los últimos 50 años ha sido construida en torno a la idea de aplicar un tiempo especial para transformar los datos de presión entonces el comportamiento de la presión durante un periodo de flujo individual puede ser similar al comportamiento dela declinación de la presión para una tasa de flujo constante. El tiempo comúnmente aplicado para este propósito no remueve completamente los efectos de la variación previa. A veces hay efectos residuales de superposición, y esto a menudo complica el análisis de la prueba.
El proceso de convertir los datos de presión adquiridos durante una prueba de tasa de flujo variable a los datos depresión equivalentes que se hubieran obtenido si el pozo hubiera fluido a una tasa constante durante toda la prueba. Es llamado deconvolución de los datos de presión. La deconvolución de la tasa de presión ha sido objeto de investigación de muchos autores en los últimos cuarenta años. Esta deconvolución se reduce a la solución de una ecuación integral. El núcleo y el lado derecho dela ecuación vienen dados por la velocidad y los datos de presión adquiridos durante una prueba. Este problema está mal condicionado, lo que significa que pequeños cambios en la entrada (prueba depresión y ratas de flujo) dan lugar agrandes cambios en los resultados de salida. El mal acondicionamiento natural del problema de la deconvolución de la velocidad de la presión, combinado con errores siempre presentes en las pruebas de velocidad y datos de presión, hacen el problema bastante inestable (Levitan M, 2005). Una variedad de algoritmos deconvolución han sido propuestos en la literatura. Sin embargo, ninguno es lo suficientemente robusto como para ser implementado en un software comercial de análisis de pruebas de pozos ampliamente utilizado en la industria (Levitan M, 2005).
Una variedad de algoritmos de deconvolución han sido propuestos en la literatura. Sin embargo, ninguno es lo suficientemente robusto como para ser implementado en un software comercial de análisis de pruebas de pozos ampliamente utilizado en la industria (Levitan M, 2005).
En este artículo se describe el proceso de diseño de un algoritmo de deconvolución que permite su uso sin problemas con datos de pruebas de pozos reales.
Se de muestran aplicaciones de análisis de deconvolución de la derivada de la presión para varios ejemplos
2. Metodología
2.1 Deconvolución de los datos depresión
En un sistema lineal, la presión de pozo durante una prueba de rata variable está dada por la convolución integral.
Donde, q (t) es la velocidad del pozo, p (t) es la presión de fondo de pozo, and p es la presión inicial de la reserva. p (t) en la Ec. 1 es la respuesta de la presión a velocidad normalizada para una producción a flujo constante, asumiendo que, al principio de la producción, el yacimiento está en equilibrio y la presión es uniforme en todas partes de este. La Ec. 1Se conoce como la integral de Duhamel's y es una expresión del principio de superposición resultante del carácter lineal del sistema.
La deconvolución de los datos de presión tiene por objeto la reconstrucción de la respuesta de la presión transitoria aflujo constante p (t) y la presión inicial del depósito p delos datos depresión y velocidad de flujo, p (t) y q (t), adquiridos durante una prueba de pozo de velocidad variable. Este problema es equivalente a resolver la Ec. 1 para p (t) con p dado p (t) y q (t) medidos durante la prueba. Muchos métodos para la solución de esta ecuación integral han sido propuestos en la literatura (Thompson L et al, 1986). Mas sin embargo, la solución dada por estos algoritmos resulta ser inestable y no podría tolerar errores que están normalmente presentes en los datos de pruebas de pozos (Kuchuk: Fetal, 1990).
2.2 Algoritmo de Deconvolución presentado por von Schroeter El nuevo algoritmo de deconvolución presentado por von Schroeter ha demostrado avances significativos en comparación con los esfuerzos anteriores. Este algoritmo está basado en varias ideas nuevas (von Schroeter Tetal, 2001).
2.2.1 Codificación apropiada de la solución. La Ec. 1 no es resuelta para la respuesta de flujo constante del sistema p?(t), sino para la función
Donde cr = ln(t). en términos dela función z(cr), la Ec. l se reduce a
La selección de z(σ) como una variable de solución asegura que dpu(t)/dlnt sea positiva, lo cual es la condición necesaria que una respuesta del sistema a flujo constante debe cumplir. Sin embargo, una consecuencia indeseable de la selección de esta variable es que la Ec. 3 pasa a ser no lineal.
2.2.2 Regularización por la curvatura. incluso por encima de la selección de la variable de solución, el problema sigue siendo mala condicionado y es muy sensible al ruido, en los datos depresión y velocidad de flujo. La imposición de restricciones adicionales en forma de una sanción a la curvatura de z(σ) impone un cierto grado de suavidad de la solución y mejora el condicionamiento del problema.
2.2.3 Formulación Total de Mínimos Cuadrados. El problema es formulado como una minimización no lineal sin restricciones con la función objetivo definida para incluir residuos de la Ec.3, los posibles errores en el flujo de datos y limitaciones de regularización de curvatura.
Existen muchos otros detalles relacionados específicamente con la implementación del algoritmo. La aplicación está dirigida a las secuencias de prueba que se estructuran similar a las pruebas de pozos convencionales, con una función q(t) a velocidad constante. La solución z(σ) es aproximada a trozos a una función lineal sobre un gráfico de puntos σi con incrementos constantes Δσ Los valores zi de la solución z(σ) en el nodo del grafico σi son determinados en el proceso de minimización. El autor usa el algoritmo de proyección variable (Bjorck A, 1996).Para minimización no lineal de mínimos cuadrados.
2.3 Método para deconvolución iterativa (Jansson)
En la Figura l. Se muestra un diagrama de bloques del proceso de deconvolución en forma iterativa. El algoritmo propuesto por Jansson se descompone en las siguientes ecuaciones (Jansson P, 1984).
En donde: es la k-ésima estimación de una observación basada en la convolución de h(m)
, en el caso en el que k = O, xº(n) = y(n){n = 1,2,3,...,N}, h(m) es el vector de la respuesta al impulso acotada por m muestras, e(n) es el criterio de error mínimo entre la salida observada y una estimación de la misma,
es el k-ésimo valor para la función de relajación la cual depende de
es la k+1 estimación de x(n) y xe (n) es la estimación final de x(n) {k = O,1,2,...,K}.
Las ecuaciones (7) -(9) se utilizaron como funciones de relajación para la restauración tres tipos de señales consideradas en este trabajo: la suma de senoides, onda cuadrada y diente de sierra respectivamente, pues estas fueron las funciones con las que se obtuvieron los mejores resultados.
En donde i representa el número de iteraciones realizadas.
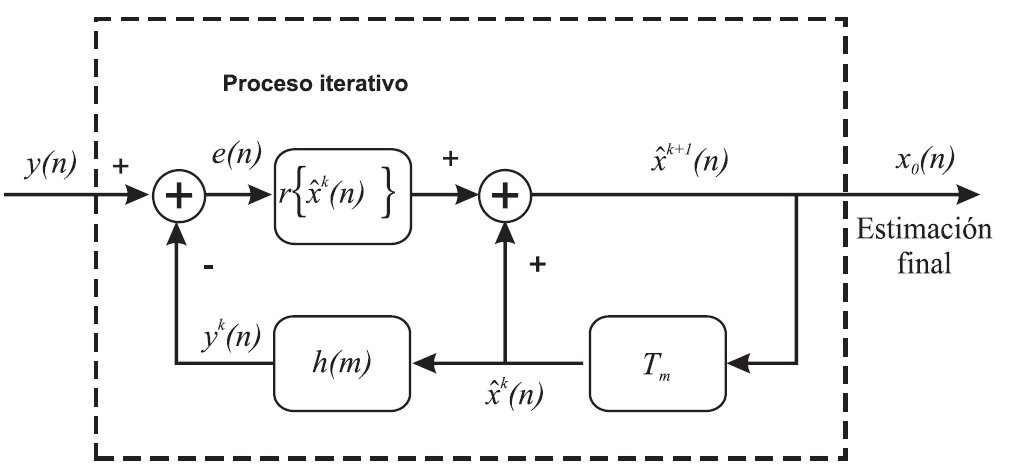
Figura l. Esquema para deconvolución iterativa
2.4 Implementación del algoritmo de deconvolución
Debemos notar, que el algoritmo diseñado para deconvolver la derivada de presión no es idéntico al algoritmo original de Jansson. Por lo tanto, el rendimiento del algoritmo generado en este trabajo es el de nuestra variante del algoritmo y no del algoritmo inicial.
El algoritmo es diferente en una serie de puntos, en lugar de usar dos procesos iterativos nuestro algoritmo solo usa uno, las realimentación usada para calcular el error es unitaria lo cual suprime el bloque h(m) usado en el algoritmo original, los datos de entradas son atenuados a rangos entre O y 1, ya que esto mejora considerablemente la eficiencia del algoritmo, los datos de salida son amplificados para eliminar la atenuación inicial en la entrada y la función de relajación usada es una variación de la función usada para la restauración de suma de senoides en el algoritmo inicial.
La Figura 2. Muestra el diagrama de flujo, donde puede verse los procesos que corresponden al diseño del algoritmo para la deconvolución.
Los datos de presión son sometidos al algoritmo de Home para determinar la derivada de presión, la deconvolución normaliza los datos de esta derivada e inicia un recorrido desde X1 primer dato hasta X''' el último dato donde m=1,2, 3, 4,......n. el último dato de la derivada, convirtiéndose en un ciclo que se repite n-esimas veces, donde se compara la entrada real con una estimada por la ecuación de relajación.
La ecuación de relajación usa 2 constantes ""C' y ""r0"". Las cuales fueron determinadas a través de una serie de pruebas con datos reales depresión, estas obtienen la constante que junto con la entrada real normalizada de la derivada se compara con el error de los valores actuales y generan el valor de salida estimada m+1 que corresponde un adelanto respecto al ciclo del algoritmo.
Esta comparación de la salida estimada y la entrada real eliminara el efecto de almacenamiento sobreponiendo los valores de la derivada deconvuelta sobre la real, realizándolo con cada valor hasta llegar al n-esimo dato deconvuelto; al llegar a esta instancia se amplifican los valores normalizado de la deconvolución a los valores correspondiente y reales.
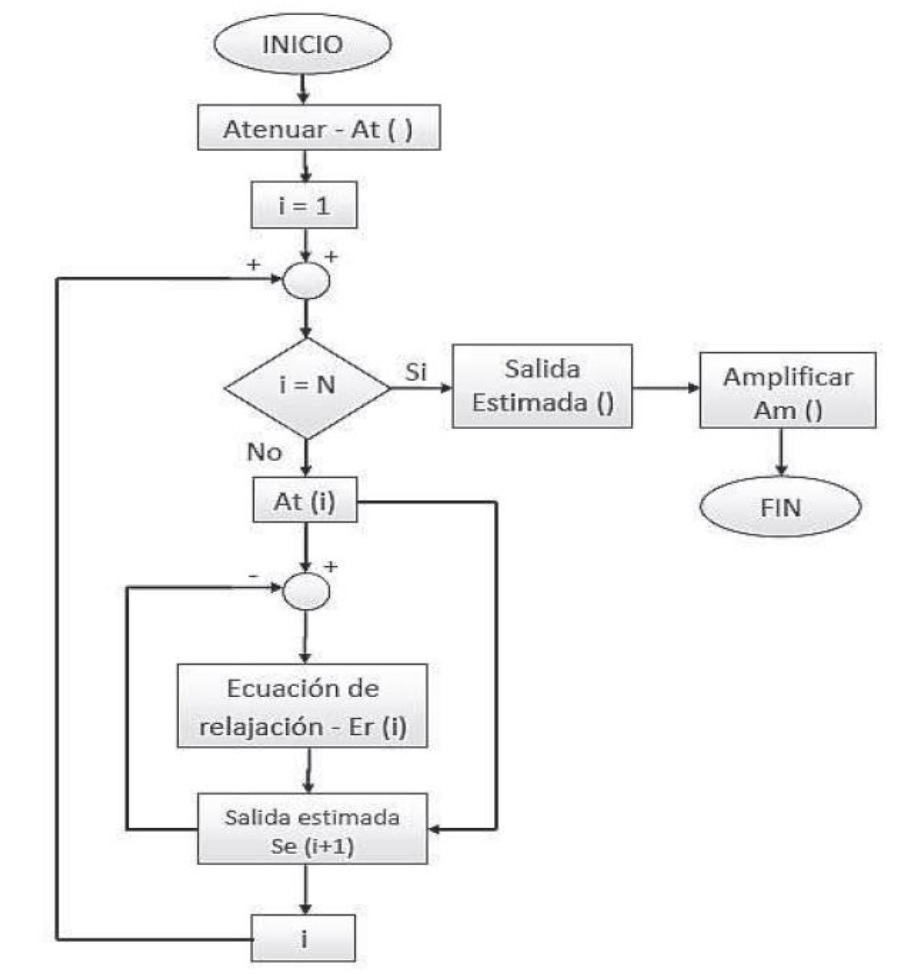
Figura 2. Diagrama de flujo de la deconvolución, donde "N" corresponde a la longitud del vector de entrada
3. Resultado
3.1 Validación del Algoritmo.
Se ilustra aquí el desempeño del algoritmo de deconvolución en dos conjuntos de datos de prueba. El primer ejemplo está diseñado para validar el código y evaluar su desempeño en datos que no han sido altamente degenerados por las perturbaciones durante la prueba, el segundo ejemplo comprueba el funcionamiento del algoritmo en datos que incluyen un alto grado de ruido.
Aplicación l. Se deconvuelve la curva que es solución para una prueba de calda de presión que consta de 64 datos de presión. Tomados a diferentes tiempos, la curva incorpora el coeficiente de almacenamiento y el factor de daño del pozo, los cuales no cambian durante toda la secuencia de prueba.
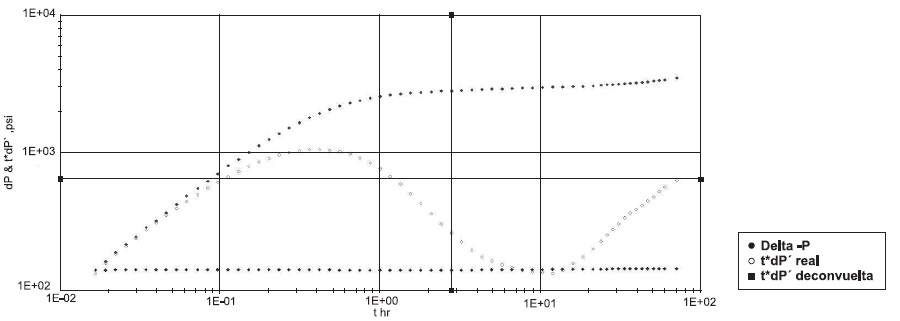
Figura 4. Gráfica (dP', t*dP' & t*dP' deconvolucionada), psi vs t,hr
La respuesta obtenida de la deconvolución muestra la usual línea recta que caracteriza el flujo radial y cómo se ha corregido totalmente el factor de almacenamiento.
Aplicación 2. Se deconvuelve la curva que es solución para una prueba de caída de presión que consta de 181 datos depresión tomados a diferentes tiempos, con un nivel significativo de ruido inmerso, al igual que en el ejemplo 1. El coeficiente de almacenamiento y el factor de daño son constantes durante todo el periodo de prueba.
Esta respuesta muestra cómo el algoritmo detecta el flujo radial que es un parámetro indispensable en el análisis de pruebas, aunque no es posible corregir totalmente el efecto de almacenamiento, esta incapacidad de restaurar totalmente la señal obedece a la elevada cantidad de ruido inmersa en los datos de prueba.
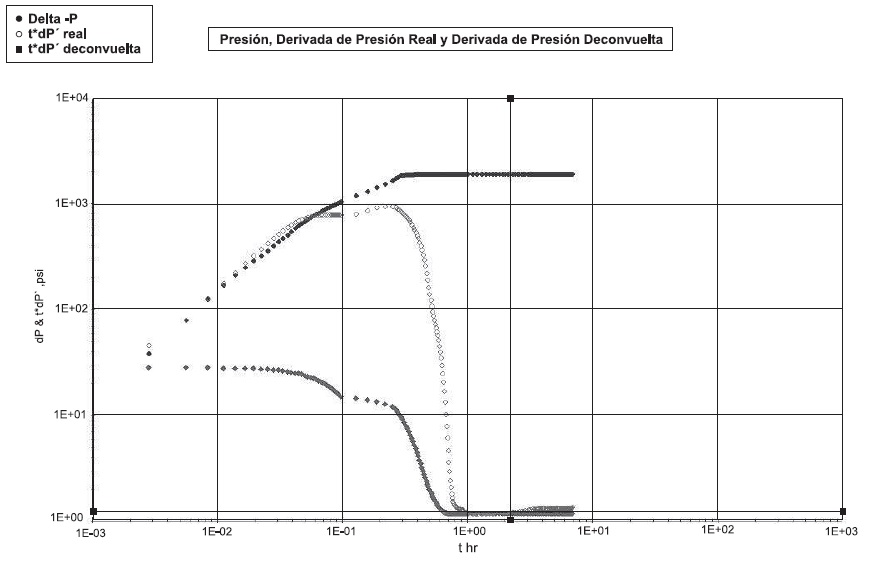
Figura 5. Gráfica (dP', t*dP' & t*dP' deconvolucionada), psi vs t,hr
4. Conclusiones
Se encontró que el algoritmo de deconvolución diseñado es extremadamente útil y de fácil uso para detectar el comportamiento de los yacimientos, lo cual abre nuevas oportunidades para el análisis permanente de datos de medidas de presión, además de ser un importante aporte para el conjunto de técnicas utilizadas en el análisis de pruebas de pozos.
Se demostró el rendimiento del algoritmo de deconvolución en las aplicaciones 1 y 2, donde los datos corresponden a pruebas reales, eliminado el efecto almacenamiento, determinando adecuadamente el factor de daño y permeabilidad de los pozos analizados.
Se logra remover parcial o totalmente el efecto de almacenamiento de los registros obtenidos durante pruebas decaída depresión o pruebas de restauración depresión.
5. Referencias Bibliográficas
1. Bjorck, A., 1996. Numerical Methods for Least Square Problems, Soc. For Industrial and Applied Mathematics (SIAM), Philadelfia, Pennsylvania. 269-279 p.
2. Jansson P.A., 1984.Deconvolution with Applications in Spectroscopy, Academic Press, Chap. 3, 4, 7, pp. 69-91, 96-132,188-225.
3. Kuchuk, F.J., Carter, R.G., and Ayestaran, L., 1990. Deconvolution of Wellbore Pressure and Flow Rate, SPEFE, 53 p.
4. Levitan, M.M. 2005. Practical Application of Pressure/Rate Deconvolution to Analysis of Real Well Test paper SPE 84290.16 presentado enel2003Annual Technical Conference and Exhibition de la SPE, Denver, 113p.
5. Thompson, L.G. and Reynolds, A.C., 1986. Analysis of Variable-Rate Well-Test Pressure Data Using Duhamel's Principle, SPEFE, 453 p.
6. Von Schroeter, T., Hollaender, F., and Gringarten, A.C., 2001. Deconvolution of Well Test Data as a Nonlinear Total Least Squares Problem, paper SPE 71574 presentado en el 2001 SPE Annual Technical Conference and Exhibition, New Orleans, 30 September-3 October. 1-1Op.