Introducción a las redes complejas: El modelo del mundo pequeño

Niber Rojas Cano

Universidad Surcolombiana, Colombia

rojascanoniber@gmail.com

Mauro Montealegre Cárdenas

Universidad Surcolombiana, Colombia

mmonteal@usco.edu.co

Se presenta en este ensayo, la historia y las herramientas matemáticas necesarias para la comprensión y posterior interpretación del modelo del mundo pequeño. Comenzando con un pequeño relato sobre la ciencia de redes junto con una definición para redes complejas, después se describen las dos propiedades características del fenómeno del mundo pequeño y finalmente se comenta y expone el modelo del mundo pequeño de Duncan J. Watts y Steven H. Strogatz.

Introducción

Desde distintos puntos de vista, el siglo XXI es sinónimo de información y globalización, al fin y al cabo, es la cuna del mundo interconectado en el que estamos inmersos y hogar de gran parte de los desarrollos tecnológicos que hoy nos tienen más conectados que nunca. Entender este periodo, la era de la conectividad como se le conoce, parece una tarea titánica, pues gran parte de los fenómenos que tienen lugar en ella, o mejor, los eventos que generan mayor interés son excesivamente complejos, sin embargo, no solo nuestro mundo cambió, también lo hizo nuestra visión científica y con ella la sorpresiva aparición de las renombradas ciencias de la complejidad se hizo inminente.

En concreto, aquí se abordará una de ellas, la ciencia de las redes, que encarna la esencia de nuestro mundo, ya que, vivimos en medio de redes tangibles, como redes eléctricas e internet, asimismo percibimos redes abstractas, como redes de conocidos, incluso, “somos nosotros, como individuos, las unidades de una red de relaciones sociales de diferentes tipos y, como sistemas biológicos, el resultado delicado de una red de reacciones bioquímicas” (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006). Precisamente por eso es importante el estudio de las redes y mucho más el análisis de uno de los dos grandes eventos que propicio su aparición, el fenómeno del mundo pequeño, de ahí que el objetivo central de esta revisión sea el de analizar e identificar cada una de las características y propiedades estructurales que debe poseer una red para que sea una red de mundo pequeño, tomando como base el modelo de redes de mundo pequeño propuesto por Duncan J. Watts y Steven H. Strogatz en el año de 1998.

Ciencia de redes

La ciencia de las redes, según Duncan Watts, “es la ciencia del mundo real, del mundo en el que viven los seres humanos de la amistad, de los rumores, de las enfermedades, de las tendencias y modas culturales y de las crisis financieras” (Watts, Seis grados de separación. La ciencia de las redes en la era del acceso, 2006). Se trata de una manera distinta de ver el mundo, donde las unidades dinámicas de un sistema y sus interacciones se sustituyen por los vértices y las aristas de un grafo, hecho “que permite pasar de los niveles individuales a las agrupaciones colectivas menos conflictivamente que otros formalismos” (Reynoso, 2008), a través de una monumental abstracción de la realidad, en la cual se desprecian los detalles y prima lo esencial, la idea es resumir la gran cantidad de detalles característicos del sistema a la simple existencia o no de un vínculo entre vértices, de ahí que sea posible obtener representaciones extremadamente sencillas de fenómenos extremadamente complejos como nuestra sociedad, la World Wide Web e incluso el cerebro humano, en consecuencia, este enfoque meramente topológico, condujo a la ciencia de redes hasta el discernimiento de propiedades aparentemente universales como el fenómeno del mundo pequeño y las redes libres de escala, características inherentes que se derivan de sistemas particularmente complejos.

El origen de todo este proceso tiene una historia bastante larga y excesivamente confusa; para los matemáticos, su punto de partida se remonta a los orígenes de la teoría de grafos, en el año de 1736, cuando como por arte de magia Leonard Euler resolvió el mítico problema de los siete puentes de Königsberg, sin embargo, lo cierto es que solo fue hasta los auspicios del siglo XXI, cuando el estudio de las redes se transformó en ciencia, debido a dos acontecimientos, el primero de ellos, la incursión de un grupo de físicos en un campo conocido como el análisis de redes sociales – ARS y el ́ultimo pero no menos importante, el desarrollo tecnológico de aquella época; de entonces acá las redes “devinieron complejas, caóticas, dinámicas y no lineales en el sentido técnico de la palabra” (Reynoso, 2008).

Así y con todo, definir qué es una red compleja, parece ser una tarea complicada, no obstante, a continuación, se presenta una definición.
Definición (Red Compleja): Una red compleja R, por lo general consiste en una gran colección de elementos heterogéneos y dinámicos relacionados a través de múltiples relaciones dinámicas y no lineales, que surgen a partir de la retroalimentación del sistema con su entorno.

Estructura de las redes complejas

A continuación, se presentan las propiedades estructurales necesarias junto con algunos conceptos fundamentales en la comprensión del fenómeno del mundo pequeño:

Distancia media

En una red, las conexiones que conectan algún par de vértices forman un camino, en ese sentido un camino geodésico es el camino más corto entre dos vértices. Dicho esto, la distancia media l cuantifica el promedio de las longitudes geodésicas en todas las parejas de vértices de la red, es decir, define el número medio de pasos que hay que recorrer a través del camino más corto para todos los posibles pares de vértices de la red. En una red no direccionada la distancia media se calcula de la siguiente manera:

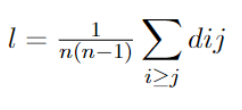
Donde n representa el número de vértices; d_ij es la distancia geodésica desde el vértice i hasta el vértice j y n(n−1) representa el número total de variaciones sin repetición de dos elementos, es decir el número de parejas distintas de vértices en la red. Nótese que, en este promedio se ha incluido d_ij=0, debido a que la distancia de cada uno de los vértices consigo mismo es cero. (Newman, 2003) (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006)

Coeficiente de agrupamiento

Heredado directamente de las redes sociales, es un concepto intuitivo que mide la tendencia de agrupación que tienen los vértices de una red. Concretamente, en una red social, determina la probabilidad que tienen dos individuos totalmente desconocidos para entablar una relación a través de un amigo en común. Su estimación tiene dos fases, local y global, en la primera se cuantifica la densidad de conexiones próximas a determinado vértice y en la siguiente se calcula el promedio de los resultados obtenidos. Así que, dada R=(V, E) una red y v_i un vértice en la red con k_i conexiones que lo conectan a él con k_i otros vértices, entonces el coeficiente de agrupamiento local está determinado por la razón entre el número |ei| de conexiones existentes entre el vértice v_i y sus k_i primeros vecinos y el número total de conexiones posibles entre v_i y sus k_i primeros vecinos, tal como se ve a continuación,

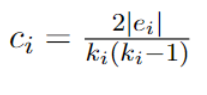
Donde 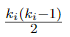corresponde al número total de aristas posibles y |ei| representa las aristas existentes. Finalmente, el coeficiente deagrupamiento de la red o coeficiente medio de agrupamiento, se obtiene a partir del promedio entre el coeficiente local y el número total de vértices de la red.

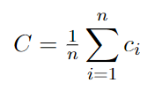
Donde C ∈ [0,1]. (Newman, 2003), (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006)

El fenómeno del mundo pequeño

Es una característica inherente a una inmensa cantidad de sistemas (Newman, 2003). Significa que a pesar de que una red esté compuesta por un gran número de vértices, la distancia media de la red alcanza valores pequeños y el coeficiente medio de agrupamiento obtiene valores altos. Inicio como una suposición sociológica, luego fue el foco de inspiración de algunos textos, después en manos de Stanley Milgram se convirtió en uno de los experimentos empíricos más importantes de la psicología social que consecuentemente se transformó en la conjetura de los seis grados de separación, la cual dice que “en este planeta estamos todos separados únicamente por seis personas. Seis grados de separación. Entre nosotros y todos los demás seres humanos de este mundo”. Al final, su punto máximo lo alcanzo calando sobre el rigor matemático, de donde se obtuvo el modelo con espíritu de universalidad que intentaremos exponer y que por supuesto alberga las propiedades citadas arriba.

El modelo del mundo pequeño

Corría el año 1998 cuando en la revista Nature se publicó el artículo Colective dynamics of ‘small-world’ networks, autoría del sociólogo Duncan J. Watts y el matemático Steve H. Strogatz; en el cual, además de corroborar la conjetura de los seis grados de separación se exponían las dos condiciones necesarias para que cualquier mundo llegara a ser un mundo pequeño.

Resulta, pues, que Watts y Strogatz tomando como base el experimento de Milgram junto con sus propias experiencias sociales, lograron concluir que, “nuestra sociedad está compuesta por un gran número de grupos que se solapan entre sí, en cuyo interior existe una alta densidad de conexiones, sin embargo, bajo esta aparente fragmentación, cualquier par de individuos puede estar relacionado a través de una corta cadena de intermediarios” (Watts, Seis grados de separación. La ciencia de las redes en la era del acceso, 2006)

Después de hacer semejante aseveración, Watts y Strogatz empezaron a desarrollar un modelo que les permitiera construir redes de mundo pequeño, sin embargo, se vieron forzados a trastear con un modelo previo, el modelo alfa como lo nombraron; con él demostraron la existencia de mundos pequeños mediante simulación dinámica a través del ordenador. El proceso reproduce el tránsito entre dos mundos heterogéneos con respecto a las interacciones sociales de sus habitantes, siguiendo una ley de interacción donde solo amigos mutuos posibilitan nuevas conexiones.

Bajo esta perspectiva, el siguiente paso, la generalización, consiguió desligar la mayor parte de las suposiciones sociológicas iniciales y así crear el modelo definitivo. Aquí se establece una relación entre interacciones ordenadas e interacciones desordenadas o en su defecto la interpolación entre una red regular y una red aleatoria a través de un proceso de reconexión de aristas con probabilidad p, ver ilustración 1. El modelo toma como base un retículo periódico unidimensional (anillo) de L vértices, en el cual cada vértice está simétricamente conectado a sus 2k primeros vecinos más cercanos, con 1≥ k ≥L, de manera que resulten Lk aristas. Luego, elegimos un vértice y la arista que lo conecta a su vecino más cercano en el sentido de las agujas del reloj. Con probabilidad p reconectamos esta arista a un vértice elegido uniformemente al azar sobretodo el anillo, excluyendo bucles, de lo contrario dejamos la arista en su lugar. De modo que si p=0, entonces no se produce ninguna modificación, y terminamos justo allí donde empezamos, un retículo perfectamente regular. En el otro extremo, cuando p=1 cualquier enlace individuales renovado y el resultado es una red muy desordenada que se asemeja a un grafo aleatorio. Para valores 0< p <1, el resultado es una red de mundo pequeño: muy agrupada como un grafo regular, pero con una distancia media pequeña como un grafo aleatorio, ilustración 1. (Boccaletti, Latora, Moreno, Chavez, & Hwang,2006), (Newman, 2003), (Watts & Strogatz, Collective dynamics of ’small-world’ networks, 1998).

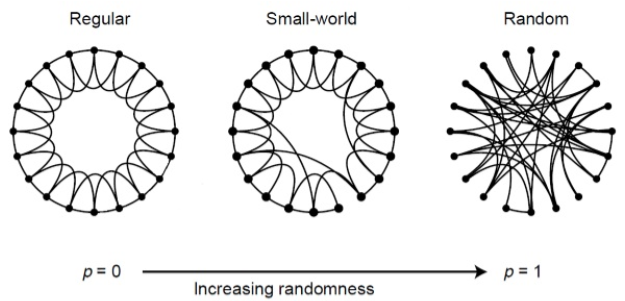
lustración 1. Construcción de redes de mundo pequeño. Adaptado de (Watts & Strogatz, 1998)

La estimación del coeficiente de agrupamiento l y la distancia media C, en función de la probabilidad p desvelaron los siguientes resultados:

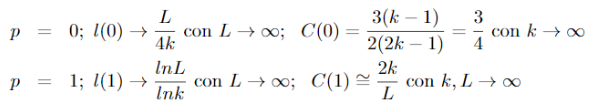
Para valores intermedios de p los resultados fueron normalizados para valores de C(0) y l(0) espectivamente. Ver ilustración 2.

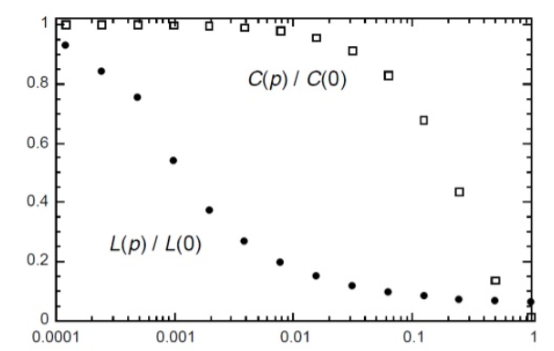
Ilustración 2. Normalización para valores de C(0) y l(0) respectivamente. Adaptado de (Watts & Strogatz, 1998)

En la ilustración 1, se puede ver la rápida caída del (p), demostrando que la red se comporta como una red de mundo pequeño. Durante la caídadel (p), C(p) permanece prácticamente constante, lo que indica que la transición a una red de mundo pequeño es prácticamente imperceptible localmente.

Conclusiones

El fenómeno del mundo pequeño es una propiedad topológica inherente a una gran cantidad de sistemas de diferentes tipos, como una red de amistad, internet, la Word Wide Web y redes metabólicas, por citar algunas; las cuales presentan un alto coeficiente de agrupamiento y una baja distancia media entre cualquier par de vértices de la red.

El fenómeno del mundo pequeño representa una propiedad global que es imperceptible de manera local, ya que el coeficiente de agrupamiento permanece constante cuando la distancia media cae abruptamente. La razón, los vértices previamente aislados han empezado a conectarse, entonces la longitud promedio entre vértices disminuye sorprendentemente, por eso es más fácil contactar o establecer relación con otros vértices distintos a los vecinos, sin embargo, cada vez son más los vértices con los que se pueden conectar, esto es, un aumento en el coeficiente de agrupamiento.

Referencias

Boccaletti, S., Latora, V., Moreno, Y., Chavez,M., & Hwang, D.-U. (2006). Complex networks: Structure and dynamics. Physics reports, 175-308.

Newman, M. E. (2003). The structure and function of complex networks. SIAM review, 167-256.

Reynoso, C. (2008). Hacia la complejidad por la vía de las redes: nuevas lecciones epistemológicas. Desacatos, 17-40.

Watts, D. J. (2006). Seis grados de separación. La ciencia de las redes en la era del acceso. México: Paidós.

Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ’small-world’ networks. Nature, 440-442.