DETERMINANTES DEL RENDIMIENTO ACADÉMICO EN NEIVA: UNA APROXIMACIÓN A TRAVÉS DE UN MODELO MULTINIVEL

RESUMEN

Este trabajo analiza (os determinantes del rendimiento académico para las áreas de lenguaje y matemáticas de los estudiantes de grado once del sector público de la ciudad de Neiva, durante el periodo 2008-2011. El objetivo general de esta investigación es determinar los factores que influyen en el rendimiento académico de la educación media para el sector de educación pública del municipio de Neiva. La metodología desarrollada se divide en dos: i) métodos de investigación etnográficos, en donde se aplicó una entrevista a una serie de agentes que tienen que ver con el proceso educativo, con el objetivo de conocer su percepción respecto a temas referentes a calidad educativa, rendimiento académico y pruebas Saber 11 y ii) métodos de investigación cuantitativos, en donde además de desarrollar la estadística descriptiva, se estimó un modelo multinivel con el que se busca determinar el peso relativo de la escuela y el hogar en el rendimiento académico de los estudiantes. Los resultados muestran que la comunidad educativa en general, presenta un grado alto de desconocimiento respecto a temas relacionados con calidad educativa y las pruebas Saber 11°. Del mismo modo se encontró que variables como la jornada académica y el ratio estudiante profesor (variables de nivel 2), acceso a internet y el género de estudiante (variables de nivel 1), son las que mayor significancia estadística y empírica presentan. Además, se encontró que el efecto colegio tiene mayor peso sobre el rendimiento académico que el efecto estudiante tanto en matemáticas como en lenguaje.

Determinants of Academic Performance in Neiva: An Approach through a Multilevel Model

ABSTRACT

This paper analyzes the determinants of academic performance in the areas of language and mathematics in eleventh grade students in the public sector of the city of Neiva, during the period 2008-2011. The overall objective of this research is to identify factors that influence the academic performance of secondary education for the public education sector of Neiva. The methodology is divided into two i) ethnographic research methods, where an interview was applied to a number of agents that have to do with the educational process in order to know their views on issues concerning quality of education, Knowing academic performance and testing 11°; and ii) quantitative research methods, where in addition to developing descriptive statistics, we estimated a multilevel model that seeks to determine the relative importance of school and home in the academic performance of students. The results show that the educational community in general, has a high degree of ignorance on issues related to educational quality and testing Saber 11°. Similarly it was found that variables such as academic day and the teacher student ratio (level 2 variables), internet access and gender of student (level 1 variables) are the greatest statistical significance and empirical present. Furthermore, we found that the effect is strongest school on academic performance that the effect both math student in language.

Key Words: Educational quality, academic performance, Saber 11 ° test, multilevel models, school factor, student factor.

INTRODUCCIÓN

El objetivo de cualquier sociedad del mundo es buscar un crecimiento económico sostenible en el largo plazo, interesados siempre por el mejoramiento del bienestar de toda su población. Algunos autores enfatizan que el crecimiento se genera en el seno de la economía bien por el capital humano (Lucas 1998), por la existencia de rendimientos constantes a escala en la función de producción (Rebelo 1991), por las externalidades tecnológicas (Romer 1986), o por la ausencia de distorsiones en el mercado (Easterly, 1993). Lucas, propone que el factor fundamental para lograr un aumento continuo del producto en el largo plazo, es la cualificación del capital humano, a mayores años de estudio mayor será la producción per cápita (productividad).

En general la educación es analizada desde tres perspectivas: i) Cobertura, ii) Eficiencia y iii) Calidad. Esta investigación se ubica en el último punto, pero no abarca su concepto en general, sino que se limita al tema del Rendimiento Académico. Es por esto que en el presente estudio se pretende determinar los factores que influyen en el rendimiento académico de la educación media en contextos de bajo desarrollo económico, en este caso se analizaron datos correspondientes al municipio de Neiva, capital del Departamento del Huila. El análisis se realizó teniendo en cuenta los resultados de la prueba Saber 11° para las áreas de matemáticas y lenguaje, estudiando solamente los estudiantes de las instituciones de educación públicas de la ciudad.

Para resolver el problema propuesto se utilizó dos métodos. Por un lado, se desarrolló del enfoque teórico de la Función de Producción Educativa propuesto por Hanusheck (1986), en donde el producto final está representado por el puntaje obtenido por el estudiante en las Pruebas Saber 11° para las áreas de lenguaje y matemáticas. Los insumos o factores productivos, están representados por las características del estudiante, de la familia y de la escuela. Por otra parte, la metodología econométrica aplicada obedece a los modelos multinivel o modelos jerárquicos, los cuales permiten realizar el análisis tanto a nivel individual como por escuela.

También se utilizaron métodos de investigación etnográficos, usando la entrevista como el método de recolección de la información. Con esto se busca conocer la opinión de los distintos agentes involucrados con la educación, en los temas referentes a la calidad educativa y el rendimiento académico.

Debido a todo lo anterior, con esta investigación se busca resolver la siguiente pregunta:

¿Cuáles son los factores que determinan el rendimiento académico de la educación media en contextos socioeconómicos menos favorables durante el periodo 2008-2011? Para resolver esto, se utilizaron los datos de los alumnos de grado once o último año de bachillerato de colegios del sector público del casco urbano de la ciudad de Neiva.

El documento se divide en seis apartados. El primero recoge la introducción; el segundo se orienta al planteamiento del problema, en el tercero se examina el referente teórico; el cuarto apartado se centra en la metodología; el quinto recoge los resultados obtenidos en el análisis empírico; y en el sexto y último, se presentan las principales conclusiones del trabajo.

PLANTEAMIENTO DEL PROBLEMA

Al revisar los resultados las pruebas Saber 11° desde el 2000 hasta el 2011, se observa que los puntajes promedio a nivel nacional, departamental y municipal tienen comportamientos similares. El promedio de la prueba de lenguaje a nivel municipal se ubicó por encima del promedio nacional y departamental para todo el periodo estudiado, a excepción del año 2009 donde el promedio nacional superó al promedio municipal y departamental. La década empezó con promedios relativamente bajos (46 puntos); fue aumentando paulatinamente hasta llegar a su punto más alto en toda la década, donde Neiva alcanzó un promedio de 52,44 puntos, 0,89 puntos más que el promedio departamental y 0,25 masque el promedio nacional. A partir de allí los promedios empezaron a disminuir producto de las diferentes metodologías y reformas que se agregaban año tras año a las pruebas. En 2010 volvió a tener un sobre salto, pero en el 2011 el departamento presentó uno de los promedios más bajos para todo el periodo estudiado. Desde este punto de vista es poco relevante que el promedio nacional siempre haya estado por debajo del promedio municipal y departamental, debido a que Colombia es un país con grandes desigualdades económicas y sociales, y seguramente este bajo promedio nacional es jalonado por las regiones más pobres del país, entre esos el departamento del Huila; aunque también se debe recalcar que la diferencia entre los tres niveles es poco significativa.

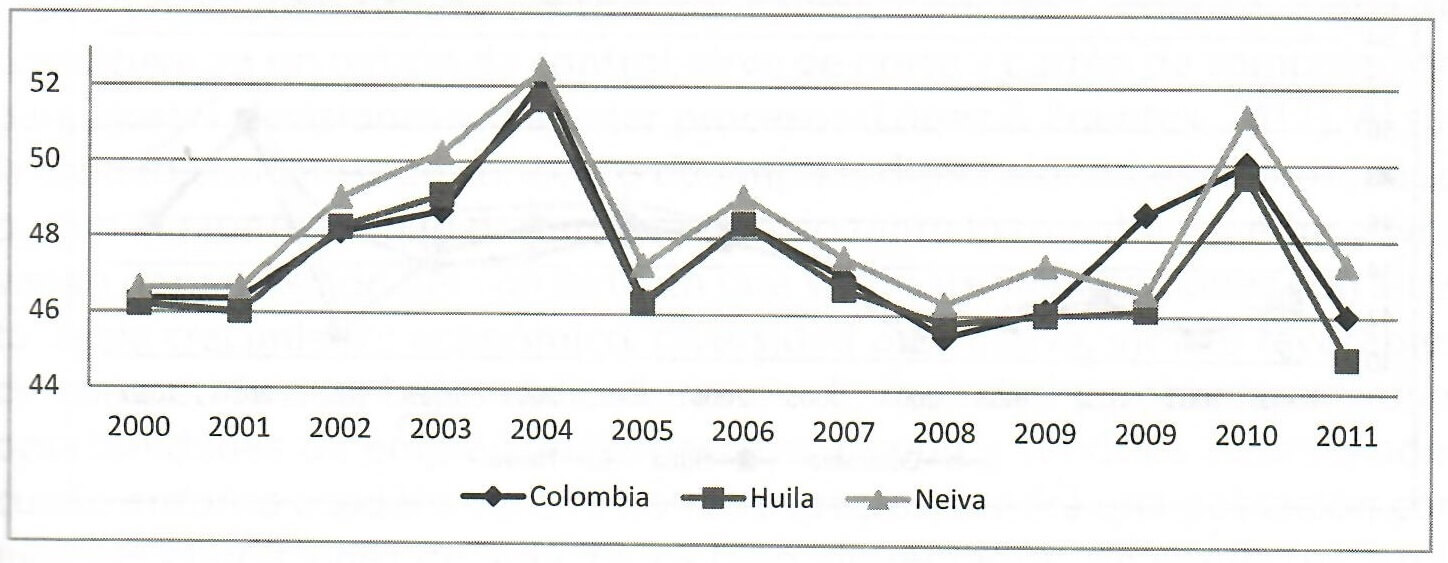
Fuente: Elaboración propia con base en los resultados históricos del ICFES.

Pero los resultados empeoran cuando se observa los puntajes de la prueba de matemáticas; el gráfico número 2 registra el comportamiento de los promedios nacional, departamental y municipal en la prueba de matemáticas para el mismo periodo anterior. Del 2000 al 2011 el promedio para cualquier nivel no superó los 43 puntos, siendo el 2004 el año en que peores resultados se registraron (41,04 puntos a nivel nacional, 40,77 a nivel departamental y 41,13 a nivel municipal). De nuevo el puntaje promedio municipal siempre estuvo por encima del promedio nacional y departamental a excepción del año 2009 donde el puntaje promedio nacional fue ligeramente superior. La diferencia promedio para todo el periodo de estudio entre Neiva y Colombia apenas llega a 0,69 puntos, mientras que entre Neiva y Huila asciende a 0,98 puntos.

De nuevo es preocupante en este análisis, el bajo puntaje promedio presentado en cada nivel; en esta ocasión el promedio de matemáticas a nivel municipal registrado en las pruebas Saber 11° llego a 44,92 puntos, 0,98 puntos por encima del promedio departamental y 0,69 por arriba del promedio nacional. Las pruebas en matemáticas presentan en promedio 3,4 puntos menos que las pruebas en lenguaje, ambas por debajo de los 50 puntos.

Fuente: Elaboración propia con base en los resultados históricos del ICFES.

Según cifras de la Secretaria de Educación Municipal, para el periodo 2001-2010, el rendimiento promedio de colegios de Neiva anualmente en promedio sólo 7% de los colegios estuvieron en la categoría muy superior, 8% en la superior, 16% en la categoría alto, 35% en el nivel medio y 34% en el nivel bajo e inferior. Estos resultados muestran una posición favorable con respecto a los promedios departamentales, aunque no deja de preocupar, la cantidad de instituciones categorizadas en los niveles bajo e inferior y la alta dispersión entre categorías.

El municipio de Neiva es una región que se caracteriza por presentar altos niveles de desigualdad y pobreza; es una de las ciudades que registra las mayores tasas de inflación y desempleo del país; la actividad económica está representada especialmente por el sector primario, en donde los sectores de explotación de minas y canteras y la agricultura, tienen la mayor participación en el PIB. La actividad empresarial se basa fundamentalmente en las organizaciones unipersonales de tipo familiar. Todos estos elementos permiten clasificar a Neiva, como una región de bajo desarrollo y crecimiento económico.

Resulta interesante preguntarnos si existe alguna relación entre el panorama socioeconómico de Neiva y el rendimiento académico de los estudiantes. Hay evidencia empírica acerca de la relación positiva que existe entre el crecimiento y desarrollo económico y social, con el desempeño académico y/o resultados escolares de una determinada región.

Autoras como Inés Aguerrondo, caracterizan la calidad de la educación como un concepto complejo totalizante y multidimensional, como concepto social e históricamente determinado, como concepto que se constituye en imagen-objeto de transformación educativa, concepto que se constituye en un patrón de control, sirve de norte y patrón de comparación para ajustar decisiones y reajustar procesos (López & Puentes, 2011). Al ser la calidad educativa un concepto de amplias dimensiones, es determinado por un conjunto amplio de variables; por lo tanto, los resultados educativos varían dependiendo del contexto en que se desarrollen. Regiones con altas tasas de crecimiento económico, diversidad productiva, índices favorables de competitividad, bajos indicadores de desigualdad y pobreza, mayores oportunidades de empleo, mayor acceso a salud y servicios básicos, adecuado entorno académico, entre otros aspectos, tendrá una población con mejores condiciones de vida, niños bien alimentados, sin conflictos familiares, y en condiciones favorables para la enseñanza educativa y el desempeño académico.

Seguros del efecto del entorno socioeconómico sobre el resultado académico, se puede argumentar sin temor a equivocarnos que el preocupante panorama económico y social de Neiva y por extensión del departamento del Huila, influye decididamente sobre una educación de mayor o menor calidad. Lo que se busca con esta investigación es tratar de responder y/o explicar a qué se deben las diferencias de rendimiento académico (puntajes en pruebas estandarizadas) entre individuos, determinando los principales factores que influyen en un menor o mayor resultado escolar.

Por lo tanto, conociendo la realidad económica y social del Municipio de Neiva, y el bajo rendimiento escolar, se busca responder preguntas como: ¿a qué se deben estas diferencias en rendimiento escolar?, ¿Cuáles son los factores que determinan un mayor o menor puntaje?, ¿La escuela tiene un peso importante sobre el rendimiento académico?, ¿Diferentes características socioeconómicas afectan diferentes áreas del conocimiento (matemáticas y lenguaje)? Además, se busca resolver al siguiente objetivo: "Determinar los factores que influyen en el rendimiento académico de la educación media para el sector de educación pública del municipio de Neiva durante el periodo 2008-2010".

REFERENTE TEÓRICO

Referentes Documentales

El aprendizaje estudiantil depende de muchos factores que en algunos casos no presentan aparentes relaciones, pero que en la práctica pueden influir; es tos elementos van desde la educación del padre y los valores de la sociedad, hasta la infraestructura escolar y el calendario agrícola. El último elemento parecería curioso, pero si se piensa en una región rural, donde económicamente depende de la agricultura, en épocas de cosechas toda la población, incluido niños y maestros, se dedican a la recolección de los productos, bien sea por escases de mano de obra, por necesidades económicas o porque el costo de oportunidad de hacer cualquier otra actividad es mayor (remuneraciones altas).

Desde la publicación del Informe Coleman, en 1966, en los estudios sobre calidad educativa se ha encontrado consistentemente que las condiciones socioeconómicas de los estudiantes y sus antecedentes familiares causan los mayores efectos sobre el rendimiento académico. Estudios posteriores a Coleman (en Inglaterra el informe Plowden y en Francia el estudio longitudinal 1962-1972, que condujo el Instituí National EtudesDámographiques-NED) demostraron de forma clara el peso del origen social sobre los destinos escolares, llegando a la misma conclusión de Coleman.

Según Vegas y Petrow (2008), la edad de entrada a la primaria puede afectar la trayectoria y los logros educativos de un niño en el sistema educativo; pero esta correlación tiene diferentes implicaciones en diferentes países. En Estados Unidos, los padres tienden a retardar la entrada de sus hijos a la escuela primaria con el fin de aumentar sus oportunidades de éxito en el colegio; en países en desarrollo por su parte, la entrada retardada al colegio se debe a factores económicos y sociales.

Fertig y Schmidt (2002), utilizando los datos individuales de PISA 2000, analizan cómo se relacionan los resultados en la prueba de lectura con la información individual y los antecedentes familiares y con las características de la escuela; encuentran que la educación materna tiene un mayor efecto en el aprendizaje general del niño, pero que la educación paterna es más importante cuando han llegado al nivel de educación terciaria.

Caro (2000), en un estudio realizado para la ciudad de Bogotá, determina los factores asociados al logro académico de los alumnos de 3° y 5° de primaria. Al igual que Fuchs y Woessmann (2005) encuentran una fuerte correlación entre los antecedentes socioeconómicos y el resultado escolar; además encuentra que el ausentismo y el trabajo infantil tienen efectos negativos en el desempeño académico de los alumnos.

Chica, Galvis, y Ramírez (2010), usando los resultados en las áreas de lenguaje y matemáticas de las pruebas Saber 11 ° para el segundo semestre del año 2009, identifican los determinantes del rendimiento académico en Colombia utilizando un modelo Logit Ordenado Generalizado. Los autores comprobaron que las variables socioeconómicas juegan un papel primordial en la calidad de la educación; tener condiciones económicas favorables afecta en gran medida la probabilidad de obtener un puntaje medio y alto tanto en matemáticas como en lenguaje, esto puede explicarse debido a que un entorno socioeconómico favorable le permite al estudiante contar con las condiciones esenciales para dedicarse a sus estudios. En este sentido, variables como tener computador en casa, nivel de ingreso y nivel de escolaridad de los progenitores se relacionan positiva y significativamente con el resultado escolar. Padres con mayor nivel educativo pueden apoyar favorablemente el proceso de enseñanza y aprendizaje de sus hijos; este mayor nivel educativo por lo general se asocia con un mayor nivel de ingreso necesario para adquirir la infraestructura suficiente como computadores, libros, etc. Los autores también concluyen que por lo general los hombres se desempeñan mejor en el área de matemáticas, mientras que las mujeres lo hacen mejor en lenguaje.

Según Sanders y Rivers (1996), las características y el comportamiento del personal docente, en especial de los maestros, influyen de manera considerable en el aprendizaje estudiantil. Un maestro ineficaz reduce potencialmente el desempeño de un estudiante durante años, pero varios maestros bajo las mismas características multiplican el efecto. Algo claro es que determinar las características y comportamientos de los maestros eficaces o ineficaces es un tema complejo, debido especialmente a la escasez de información, en especial en los países en desarrollo, debido a esto son pocas las experiencias que avalan el impacto de variables especificas del maestro sobre el resultado escolar.

"Calidad de la Educación y Rendimiento Académico en Bogotá", estudio realizado por Gavira y Barrientos en 2001, estudian los efectos del entorno familiar y las características del plantel sobre el rendimiento escolar en Bogotá, con base en los resultados de las Pruebas Saber 11° para el año 1999. Tres conclusiones principales se desprenden del trabajo, i) la educación de los padres tiene un efecto sustancial sobre el rendimiento académico, ii) el efecto de la educación de los padres se transmite principalmente a través de la calidad de los planteles educativos y iii) la incidencia de los planteles sobre el rendimiento supera la incidencia conjunta de las características familiares y es mayor que la observada en otros países. Según los autores, estas tres premisas sugieren que, la existencia de restricciones en el acceso a la buena educación constituye un factor muy importante de inmovilidad social en Colombia.

Las tecnologías de información y comunicaciones (TIC) tienen gran potencial para mejorar los procesos de aprendizaje. Según Hepp y otros (2004), la inversión en TIC en la educación se considera como una forma primaria de preparar a las personas para las nuevas necesidades del mercado laboral y permitir que regiones rezagadas desarrollen las competencias necesarias para igualar las oportunidades de acceso al empleo. Fuchs y Woessmann (2004), hallaron que el uso de computadores en el colegio no tiene efecto alguno sobre el puntaje del PISA; por el contrario, el uso de computador en casa, en especial con acceso a internet, correo electrónico y software educativo, garantiza un mayor rendimiento académico.

Pineros y Rodríguez (1999), encuentran que "las escuelas tienen un efecto pequeño pero considerable sobre el logro académico, teniendo entre 15% y 18% de la varianza entre alumnos en escuelas privadas y 12% y 16% en escuelas públicas", Otro de los hallazgos del estudio son las grandes diferencias de desempeño en las pruebas que hay entre y dentro de las escuelas especialmente del sector privado; esto puede deberse a las diferencias en dotación física de los establecimientos educativos. La infraestructura académica y los materiales didácticos muestran una correlación positiva con el logro escolar; por tanto, laboratorios de ciencias, bibliotecas, instalaciones deportivas, tiene un efecto estadística y empíricamente significativo y positivo sobre el rendimiento académico de los alumnos; es decir, un suministro adecuado de insumos repercute positivamente en el logro escolar. Los autores también sostienen que los estudiantes matriculados en escuelas de jornada completa muestran un rendimiento significativamente mayor que los estudiantes matriculados en escuelas con jordanas de medio día.

López (2010), a partir de las pruebas nacionales del ICFES Saber 11° desde 1980 a 2009, estima el porcentaje de la variabilidad del logro académico atribuible al plantel educativo dentro de un análisis multinivel discriminado por sector educativo. El "efecto colegio" ha sido siempre mayor para el promedio total de la prueba que para el área de matemáticas, esto sugiere que el colegio tiene menos espacio en el rendimiento de los estudiantes en pruebas de matemáticas, siendo sus condiciones innatas el mayor determinante en el rendimiento. Otro punto importante es el cambio de forma y fondo realizado a las pruebas de Estado después de la última década; estos cambios de metodología incidieron en los resultados de las pruebas, pues los puntajes promedios bajan drásticamente en especial en el sector público lo que produce que el coeficiente del factor colegio baje considerablemente en ambos sectores, siendo constantes hasta el final de la década; entonces a partir del 2000 se modificó la importancia del colegio en el rendimiento académico de los estudiantes colombianos.

Marco Teórico

El aporte de Hanushek (1986) es una referencia obligada para el tratamiento económico de la educación ya que da las pautas y menciona los problemas a los que se puede enfrentar el investigador "La economía puede analizar la educación con un enfoque de insumo-producto, es decir, un marco en el cual la calidad de la educación es determinada por una serie de factores” (Hanushek, 1986).

Una función de producción en educación se refiere al análisis estadístico que permite observar los resultados de los estudiantes3 Estos resultados se derivan por lo general de las pruebas estandarizadas..., en función de un conjunto de características que pueden ser propias como la edad, el sexo, características familias y de la escuela. De lo expuesto se desprende que su uso en el campo educativo ha sido potencial para el análisis y definición de políticas.

El gráfico N. 3, representa la función de producción en educación desarrollada por Hanushek en 1978. En este tipo de investigaciones, el nivel de desagregación generalmente se presenta a nivel del estudiante (tomando promedios escolares, test en las asignaturas necesarias, resultado de pruebas estandariza-das, etc.) o captando promedios por zonas.

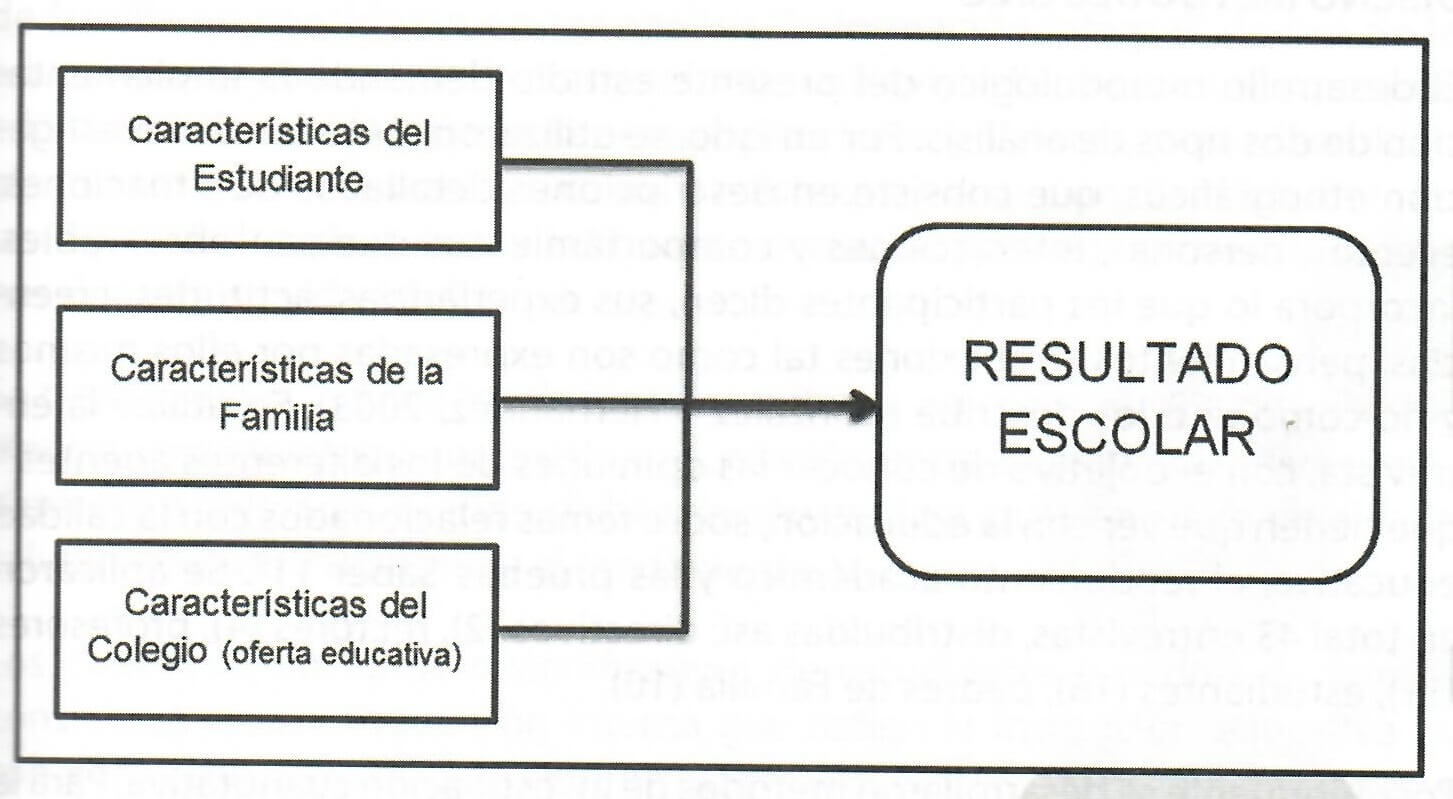
Fuente: Hanushek (1978).

El modelo conceptual generalmente aceptado para establecer la función de producción en educación tiene la siguiente especificación:

Donde, i representa el i-ésimo estudiante y t el periodo de tiempo,

= resultado escolar en el tiempo t

= vector de características familiares en el tiempo

= vector de compañeros de aula en el tiempo

= vector de insumos escolares en el tiempo

= vector de habilidades innatas

Esta forma funcional relaciona los resultados escolares a nivel del estudiante con grupos de variables o insumos con los cuales se establece una relación teórica directa (familia, compañeros, insumos escolares y habilidades innatas).

DISEÑO METODOLÓGICO

El desarrollo metodológico del presente estudio demando la implementación de dos tipos de análisis. Por un lado, se utilizaron métodos de investigación etnográficos, que consiste en descripciones detalladas de situaciones, eventos, personas, interacciones y comportamientos que son observables. Incorpora lo que los participantes dicen, sus experiencias, actitudes, creencias, pensamientos y reflexiones tal como son expresadas por ellos mismos y no como uno los describe (González y Hernández, 2003). Se utilizó la entrevista, con el objetivo de conocer las opiniones de los diferentes agentes4 Se entrevistaron a directivos, rectores, profesares, estudiantes y padres de familia..., que tienen que ver con la educación, sobre temas relacionados con la calidad educativa, el rendimiento académico y las pruebas Saber 11°. Se aplicaron en total 43 entrevistas, distribuidas así: directivos (2), rectores (4), profesores (11), estudiantes (16), padres de Familia (10).

Posteriormente se desarrollaron métodos de investigación cuantitativa. Para la aplicación de este método se consultó dos fuentes de información: i) al ICFES quien suministró la información de orden personal y socioeconómico de los individuos, junto con su respectivo resultado en las pruebas Saber 11 ° para cada uno de los años objeto de análisis; ir) a la Secretaria de Educación de Neiva, donde distribuyeron la información referente a la planta docente de cada una de las instituciones públicas de educación media de la ciudad.

Una vez compilada la base de datos, el paso a seguir fue caracterizar la población objeto de estudio a través de la estadística descriptiva. Posteriormente, se estimó un modelo multinivel de dos niveles explicativos (nivel estudiante y nivel escuela) del rendimiento en lenguaje y matemáticas usando el puntaje en la prueba Saber 11 con el objeto de determinar cuáles de las variables escolares e individuales afectan el rendimiento académico de los estudiantes. Para el desarrollo estadístico, se consideró un número total de estudiantes de 11.195, distribuidos así 2.758 en 2008, 3050 en 2009, 2,804 en 2010 y 2.583 en 2011; los estudiantes estuvieron matriculados en las 23 instituciones de educación pública que se analizaron durante todo el periodo de estudios.

RESULTADOS

Análisis de las Entrevistas

Los resultados de las entrevistas realizadas, permiten argumentar que es preocupante la concepción de calidad educativa que tienen los agentes entrevistados. Un poco más de la mitad de los rectores, profesores y padres de familia no consideran en sus análisis "la formación integral" dentro de la educación de calidad. Todas las personas entrevistadas insisten en que una educación de calidad tiene inmersos principios y valores, pero descuidan elementos que se desarrollan cuando existe una educación de calidad, como las capacidades, destrezas y actitudes necesarias para equiparar a los jóvenes durante su vida adulta.

Se resalta que el 25% de los docentes y rectores, así como el 10% de los estudiantes consideren que no existe una relación entre calidad educativa y rendimiento académico, cuando dicha relación es clara, pues en cierta medida la calidad educativa determina el rendimiento.

Los directivos, un número significativos de estudiantes y padres de familia consideran que la evaluación interna que realiza la institución educativa es coherente con la evaluación externa que realiza el ICFES. El problema con esta afirmación es que según ellos dicha relación se explica por su parecido en el tipo de preguntas que aplican. Se supone que las pruebas Saber 11 “están diseñadas para medir ciertas competencias y saberes de los estudiantes; su diseño y aplicación tienen una regularidad de alto nivel que la hace diferente a una simple preguntas con respuesta de selección múltiple. Esto lo que demuestra es que existe un desconocimiento total por el tipo de preguntas que realiza ICFES, es probable que directivos y padres de familia nunca hayan leído una pregunta de la prueba Saber 11° y que los estudiantes recién las conozcan el día que presentan la prueba, por tanto, ante este desconocimiento es difícil hacer una comparación clara y coherente entre los métodos internos y externos de evaluación.

Es interesante señalar que los directivos, rectores, docentes y estudiantes dicen conocer la estructura e intencionalidad de las pruebas saber 11°, pero realmente no tienen claro cuál es la intención de la prueba ni mucho menos su estructura. Respeto a la intencionalidad se limitan a comentar que es una prueba que evalúa el conocimiento de los estudiantes, sirve para ingresar a la educación superior y miden ciertas competencias que en muy pocos casos mencionan. En cuanto a la estructura no se hicieron referencias claras.

De acuerdo con los determinantes de la calidad educativa, todos los agentes le dan prioridad especialmente a los factores de la escuela (infraestructura y profesores) y de la familia, aspectos importantes en la generación de una educación de calidad. Hay ciertos factores a los que no les dan mayor importancia, como el aporte del estudiante, los factores sociales, las condiciones socioeconómicas entre otras.

Respecto al papel que juega el gobierno departamental y municipal en el mejoramiento del rendimiento académico, se limita no solo a acompañar el proyecto educativo en general, sino también a intervenir en el mejoramiento de los ambientes escolares (tanto de planta física como de profesores) necesarios para un mejor desempeño académico tanto de estudiantes como de instituciones educativas. Sin duda el papel del Estado es importante, pero a nuestro parecer descuida elementos fundamentales que también contribuyen en la calidad educativa y el rendimiento académico de los estudiantes tales como el mejoramiento de las condiciones socioeconómico de los estudiantes.

La mayoría de los profesores coinciden en afirmar que los métodos de evaluación los diseñan pensando en que van a cumplir con los lineamientos de las pruebas Saber 11°. Resulta interesante preguntarse si es pertinente educar a los estudiantes pensando en que deben responder eficientemente a una prueba, o si el tipo de preguntas que los mismos docentes desarrollan cumplen con las características de las preguntas implementadas por el ICFES.

Tres cuartas partes de los estudiantes están de acuerdo con la manera como los evalúan en la institución educativa, pues según ellos, en la evaluación se tratan los temas aprendidos en clases. Otro número considerable de estudiantes manifiesta que la evaluación interna es tipo ICFES, esto les permite repasar para la prueba Saber 11°. Tanto los estudiantes como los profesores, olvidan ciertos aspectos que deben contener los procesos de evaluación, necesarios para garantizar una adecuada formación académica.

Análisis Estadístico Descriptivo

El análisis estadístico descriptivo permite caracterizar la población objeto de estudio, en este caso, los estudiantes del grado once de las instituciones de educación pública de la ciudad de Neiva.

AÑO	Puntaje Matemáticas		Puntaje Lenguaje		% Estudiantes
2008	45,74	-	46,15	-	24,64%
2009	45,18	-0,50	46,94	0,8	27,24%
2010	46,43	0,69	46,21	0,07	25,05%
2011	48,55	2,81	47,21	1,06	23,07%

El cuadro N. 1 muestra el porcentaje de estudiantes analizados distribuidos a lo largo del periodo evaluado (última columna). Se puede observar una distribución con proporciones similares y cierta tendencia a la baja a medida que transcurren los años. Esta reducción en el número de estudiantes, se puede explicar por la disminución en las tasas de matrícula que se registraron en los últimos años en la ciudad. Del cuadro también se observan los puntajes promedios por área de conocimiento evaluada para cada uno de los años; los puntajes de lenguaje y matemáticas tendieron a aumentar, siendo más significativo el aumento en matemáticas, donde el puntaje promedio para el año 2011 llego a 48,55 puntos, 2,81 puntos por encima del puntaje promedio registrado en el año 2008.

En el 2008 el 55% del total de estudiantes eran mujeres, mientras que para el 2011 la cifra aumentó a 58%. Los hombres (47,64) tienden a obtener un puntaje promedio más alto en matemáticas que las mujeres (45,48) tal y como se muestra en otros estudios; mientras que en lenguaje tanto hombres (46,63) como mujeres (46,62) tienden a obtener resultados similares.

La edad promedio de los estudiantes durante el periodo 2008-2011 es de 16,76 años. El 97% de los estudiantes tiene 19 años o menos, y el 82% tiene menos de 17 años. A medida que la edad de los estudiantes aumenta, el puntaje promedio para las dos áreas evaluadas disminuye; pero esta diferencia es más pronunciada en matemáticas que en lenguaje.

El 47% de los padres de familia de los estudiantes de grado once de la ciudad de Neiva, tienen un nivel educativo de secundaria, el 32,9% alcanzaron primaria. Solo el 9,15% de los papás de familia tiene algún tipo de educación superior. El impacto de la educación del padre de familia sobre el rendimiento de los estudiantes,es mayor en matemáticas que en lenguaje. Los estudiantes cuyo padre tienen nivel de educación primaria (44,97),obtienen en promedio 4,39 puntos menos en matemáticas que los estudiantes con padre de nivel de educación superior; mientras que los estudiantes con padre de nivel de educación superior (48,79), obtiene en promedio 3,16 puntos más en lenguaje que aquellos estudiantes cuyo papá solamente alcanzó el nivel de educación de primaria.

El 54,4% de los estudiantes de grado once de la ciudad de Neiva, tienen madres con nivel de educación de secundaria, el 28,8% tienen madres que solamente alcanzaron el nivel de educación de primaria. La proporción de padres con nivel de educación superior (9,15%) es mayor a la proporción de madres con el mismo nivel de educación (8,1%), La evaluación de la madre tiene un mayor impacto en el rendimiento de matemáticas del estudiante. Los estudiantes con madres de nivel de educación superior (49,55), obtienen en promedio 4,92 puntos por encima del puntaje promedio de estudiantes con madres de nivel de educación de primaria, y 5,53 puntos más que aquellos estudiantes con madres que no presentan ningún nivel de educación en el área de matemáticas. Los alumnos con madres que no registran ningún nivel de educación (44,74), obtienen en promedio 2 puntos menos en lenguaje que aquellos alumnos con madres de nivel de educación secundario, y 4 puntos menos que las madres con nivel de educación superior.

El 95,23% del total de estudiantes pertenecen a estratos socioeconómicos 1 y 2, mientras que sólo el 0,68% pertenecen a los estratos 4, 5 y 6. Como era de esperarse, las características en las regiones poco desarrolladas y con problemas económicos y sociales, la mayoría de su población se clasifican entre los estratos socioeconómicos más bajos. Los estudiantes de estrato socioeconómico 6 obtienen en promedio 48,33 puntos en lenguaje, 2,5 puntos por encima de los de estrato 1, y 1,32 puntos más que los estudiantes de estrato 2. En cuanto a los resultados de matemáticas, los estudiantes de estrato 3 (48,03) obtienen en promedio 3 puntos más que los estudiantes de estratos 1, y 0,94 puntos más que los estudiantes de estrato 2.

Un poco más del 80% de los alumnos convive en hogares que cuentan con menos de 2 salarios mínimos legales vigentes. El 51,78% de los estudiantes vive en hogares que cuentan con ingresos entre uno y menos de dos salarios mínimos. Sólo el 14,22% de los hogares analizados, reciben como ingresos entre dos y menos de tres salarios mínimos; a su vez el 5,44% de los hogares reciben ingresos mayores a 3 salarios mínimos. Del gráfico N. 4 se observa que, a mayores ingresos económicos del hogar, mayores rendimientos académicos se registran.

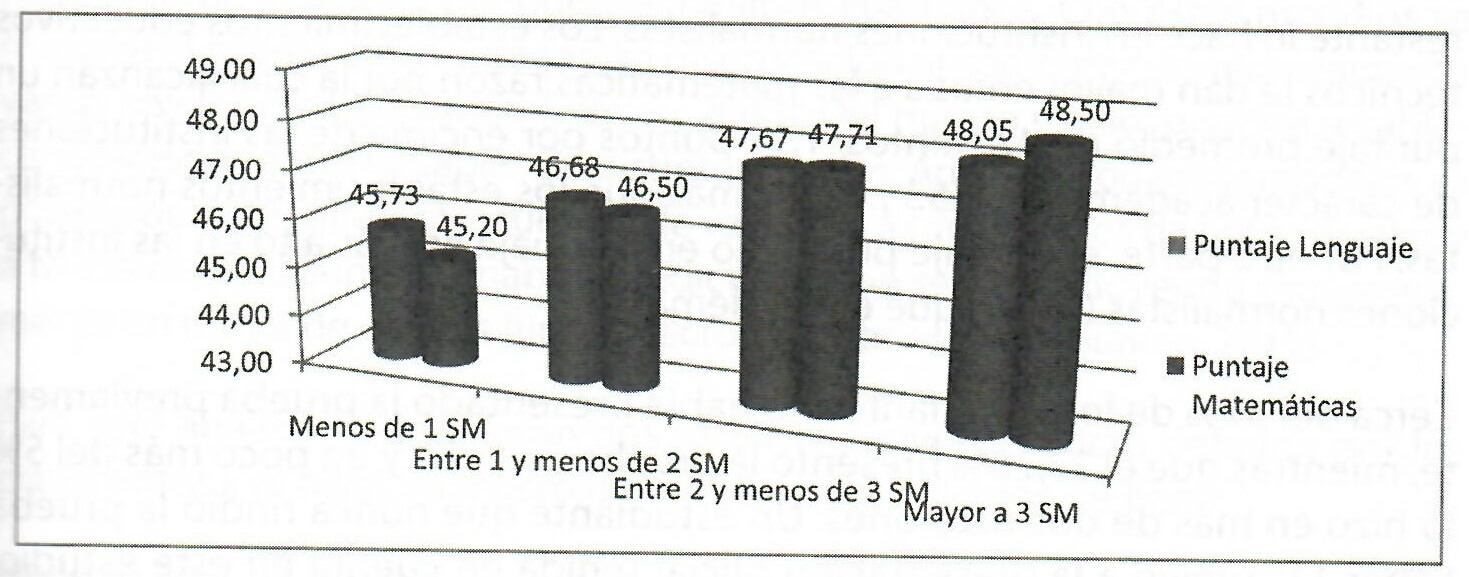
Los estudiantes con computador en el hogar, obtiene en promedio 47,4 puntos en lenguaje, 1,49 puntos por encima de aquellos estudiantes que no tienen computador. El efecto sobre el puntaje de matemática es mayor, los alumnos con computador en el hogar obtuvieron 47,72 puntos, 2,51 puntos más que los alumnos que no tienen computador. Tener internet en casa implica obtener en promedio 47,33 puntos en matemáticas, 1,6 puntos por encima de los estudiantes sin acceso a internet. En el área de lenguaje, dicha diferencia alcanza los 1,42 puntos.

Entre el año 2008 a 2011, el 7,2% de los estudiantes trabajó. Del total de estudiantes que trabajan, el 45,78% son mujeres, y el porcentaje restantes son hombres. El 88,51% de los estudiantes mayores de 22 años trabajan, y obtienen en promedio menos puntaje que aquellos estudiantes que no trabaja. Este efecto es mayor en matemáticas, debido a que los estudiantes que trabajan (4434) obtienen en promedio 2,23 puntos menos que aquellos que no trabajan. En lenguaje, los estudiantes que no trabajan obtienen 1,96 puntos más que aquellos estudiantes que si lo hacen (44,81).

Cerca del 46% de los estudiantes pertenecen a la jornada mañana, un 30,92% pertenecen a la jornada de la tarde, el 20,10% a la jornada completa, y el 2,99% a la jornada nocturna o sabatina. Los estudiantes de jornada completa obtienen en promedio 47,07 puntos en lenguaje, 0,49 puntos por encima de los estudiantes de la jornada mañana y 4,23 puntos por encima de los estudiantes de la jornada nocturna o sabatina. En matemáticas, los estudiantes de la jornada tarde obtienen un puntaje promedio de (47,21), 7,67 puntos más que los estudiantes de la jornada nocturna y sabatina.

El 67,59% de los estudiantes, asiste a clases en instituciones de educación técnica, y el 26,86% lo hace en instituciones de carácter académico, el porcentaje restante lo hace en instituciones normalistas. Los establecimientos educativos técnicos le dan mayor énfasis a las matemáticas razón por la cual alcanzan un puntaje promedio de 47 puntos, 1,97 puntos por encima de las instituciones de carácter académico y 1,53 puntos más que los establecimientos normalistas, Por otro parte, el puntaje promedio en lenguaje es más alto en las instituciones normalistas (47,40) que en las demás.

Cerca del 67% de los estudiantes no había presentado la prueba previamente, mientras que el 27,26% presentó la prueba una vez, y un poco más del 5% lo hizo en más de dos ocasiones. Un estudiante que nunca rindió la prueba Saber 11° previo a la presentación oficial tenida en cuenta en este estudio, obtiene en promedio 45,29 puntos en matemáticas, 2,78 puntos menos que quienes la presentaron una vez, 5,83 puntos menos que aquellos estudiantes que rindieron la prueba dos veces, y 8,51 puntos por debajo de los estudiantes que presentaron la prueba tres veces o más. El puntaje promedio de lenguaje de los estudiantes que nunca presentaron la prueba, alcanza los 45,9 puntos, 1,95 puntos menos que aquellos estudiantes que presentaron la prueba una vez, y 4,41 puntos por debajo de los alumnos que rindieron la prueba tres veces o más.

Al observar el puntaje promedio de matemáticas distribuidos por grupos de estudiantes, los resultados indican que grupos de alumnos de matemáticas de 20 a 25 personas, obtienen un puntaje promedio de 48,13 puntos, 4,2 puntos por encima de grupos con menos de 15 estudiantes, y 2,14 puntos más que los grupos con más de 30 alumnos. En cuanto al puntaje promedio de lenguaje, se encontró que los grupos de alumnos de lenguaje con más de 30 estudiantes obtuvieron un puntaje promedio de 47,16 puntos, un punto más que los grupos con menos de 15 estudiantes, y 0,15 puntos por encima de grupos de alumnos entre 20 y 25 individuos.

Análisis Multinivel

En los inicios de la investigación sobre eficacia escolar y rendimiento educativo se utilizó el modelo de regresión múltiple con datos de estudiantes sin agregar, mediante un procedimiento de mínimos cuadrados (e.g. Coleman et al. 1966 y Jencks et al. 1972). Esta estrategia olvida el contexto en el que la conducta se desarrolla. Esto implica que la matriz de varianza - covarianza de los resultados no refleja la homogeneidad intragrupos, es decir, olvida la correlación intragrupos.

Los modelos multinivel resuelven este y otros problemas que se presentan al momento de aplicar el método de mínimos cuadrados. Con estos modelos se resuelve el dilema entre agregación disgregación al combinar simultáneamente varios niveles (Vallejo, Arnau & Bono, 2008). Del mismo modo, permite establecer relaciones entre variables de distintos niveles. Además, con estos modelos es posible detectar diferentes fuentes de variación a través de los distintos niveles y a través de las distintas variables predictoras que se van incluyendo progresivamente en forma de efectos fijos o efectos aleatorios (Peña Suarez, 2011).

Para este análisis se definieron dos niveles: el nivell o micro definido por los estudiantes y el nivel 2° macro definido por los colegios, se tiene:

Nivel 1:

     Variables Individuales (1)

Nivel 2:

     Var. Grupales (2)

Remplazando (2) en (1), y reordenando, se obtiene la formulación convencional de un modelo multinivel, en donde al principio se colocan los efectos fijos, y al final los efectos aleatorios (entre paréntesis):

      (3)

En donde, Y_ij representa el puntaje en la prueba saber del estudiante i que pertenece al colegio j para las áreas de matemáticas y lenguaje; X_ij representa el conjunto de variables de nivel 1 que caracterizan al estudiante i que pertenece al colegio j; W_J son el conjunto de variables de nivel 2 que caracterizan la institución educativa j; y_00 es el rendimiento medio en la población de escuelas; U_0j rendimiento diferencial de la escuela j; y_01 es el incremento o disminución en el rendimiento esperado de la escuela por cada unidad que aumente W; y_10 es el incremento en el rendimiento del estudiante por el aumento de X en la población de escuelas; U_1j es el incremento diferencial en el rendimiento de estudiante por el aumento en X en la escuela j; y_11 es el incremento o disminución en el rendimiento por cada cambio en X y W, ε_ij variación residual del estudiante i, es decir lo que se aparta del rendimiento esperado según su X, donde ε_ij∼N(0, σ_ε^2), se asume varianza homogénea para todas las escuelas.

Análisis de Datos

Los modelados multinivel suelen componerse de una serie de pasos comunes recogidos entre distintos autores (Heck&Scoot, 2000; Kim, 2009; Murillo, 2007); en vista de esto, a continuación, se estiman una serie de modelo partiendo del más simple al más complejo. Estos modelos se estimaron utilizando el software IBM SPSS Statistics 19.

El modelo multinivel más simple se obtiene substrayendo del modelo (3) el conjunto de variables independientes y. De esta forma se obtiene un modelo sin variables independiente que recibe el nombre de modelo incondicional o nulo.

Las estimaciones del modelo nulo, que incluye el efecto del factor colegio, arrojaron unos valores para el -2LL5 Estadísticos de ajuste global indican en qué medida el modelo... de -9011,041 para lenguaje y- 3124,649 para matemáticas, este valor obedece al modelo que incluye la constante y el factor de efectos aleatorios. El efecto del colegio puede evaluarse comparando el modelo que incluye ese efecto con el modelo que no lo incluye. El valor del estadístico -2LL del modelo que únicamente incluye la variable dependiente y la constante asciende a -8591,82 para lenguaje y -2498,38 para matemáticas6 Para obtener estos valores basta can ajustar el modela que únicamente.... La diferencia entre ambos valores es de 419,22 en el caso de lenguaje y 026,26 en el caso de matemáticas, estos valores se distribuyen según chi-cuadrado con 1 grado de libertad (el que corresponde al parámetro asociado al factor colegio, que es el único parámetro en el que difieren ambos modelos). La probabilidad de encontrar valores chi-cuadrado ¡guales o mayores a 455,61 y 673,91 es menor a 0.0005; por lo tanto, se puede rechazar la hipótesis nula de que el efecto del factor colegio es nulo.

El cuadro número N. 2, muestra el valor estimado de la constante, que es el único parámetro de efectos fijos que presentan estos dos modelos (el que utiliza el logpuntleng y el logpuntmat como variable dependiente). Esta constante no es otra cosa que la estimación de la media poblacional de las 23 instituciones educativas en el rendimiento de lenguaje () y matemáticas ()7 Este valor expresa la media en logaritmo; en valores naturales la media.... Dicha estimación aparece acompañada de su error típico, los grados de libertad su valor tipificado (que se obtiene dividiendo la estimación entre su error típico) y el nivel crítico obtenido al contrastar la hipótesis de que el parámetro vale cero. En este caso esto nos indica que el puntaje promedio tanto de lenguaje como de matemáticas es mayor a cero.

Modelo	Parámetro	Estimación	Error típico	gl	t	Sig.
Puntaje Lenguaje	Intersección	3,816676	,008876	21,872	430,013	,000
Puntaje Matemáticas	Intersección	3,791713	,013024	21,875	291,135	,000

El cuadro N. 3 ofrece las estimaciones de los parámetros de covarianza, es decir, las estimaciones de los parámetros asociados a los efectos aleatorios del modelo. La varianza del factor colegio indica cuanto varía la variable dependiente entre los colegios de toda la población, para el puntaje de lenguaje la varianza del factor colegio es 0,001725 y para matemáticas es de 0,003753. La varianza de los residuos indica cuanto varía la variable dependiente dentro de cada colegio, para el puntaje de lenguaje la varianza de los residuos es 0,02599 y para matemáticas es de 0,04395. Los resultados indican que hay una mayor varianza entre y dentro de los colegios en el puntaje de matemáticas que en el puntaje de lenguaje. La variabilidad entre las instituciones educativas en el rendimiento en lenguaje representa el , o 6,22% de la variabilidad total, mientras que en matemáticas representada el o 7,867% de la variabilidad total8 Este cociente recibe el nombre de coeficiente de correlación....

Modelo	Parámetro		Estimación	Error típico	Wald Z	Sig.
Puntaje Lenguaje	Residuos	Varianza	,025990	,000348	74,739	,000
	InstituciónEducativa		,001725	,000547	3,151	,002
Puntaje Matemáticas	Residuos	Varianza	,043951	,000588	74,739	,000
	InstituciónEducativa		,003753	,001179	3,184	,001

Del cuadro N. 3 se puede extraer información que permite contrastar la significancia de cada estimación. Se quiere contrastar la hipótesis H_0:σ_β^2=0, de que la varianza poblacional del factor colegio vale cero. Para esto se utiliza el estadístico Z de Wald. Dado que la significancia es menor a 0,05, se puede rechazar la hipótesis nula y afirmar que la varianza del factor escuela es distinta de cero. De esta forma se concluye que el rendimiento académico no es el mismo en todas las instituciones académicas.

Ya se comentó que existen diferencias entre las medias de los colegios que ofrecen grado once en la ciudad de Neiva; ahora se estimó el modelo: medias como resultados (RMR) con el que se busca determinar si esta variación se debe a la incorporación de variables de nivel 2. Para esto se agregaron inicialmente las variables Ratio estudiante/profesor, Jornada Académica de la Institución Educativa, Tipo de bachiller de la Institución Educativa. De las primeras estimaciones resultaron ser no significativas el tipo de bachiller de la institución educativa en ambos modelos, y el ratio estudiante/profesor en el modelo de lenguaje.

El cuadro N. 4 muestra el resultado de dichas las estimaciones. La primera parte del cuadro describe el modelo RMR utilizando como variable dependiente el logaritmo del rendimiento en lenguaje. La intercepción arrojó un resultado de 3,709, mientras que las variables explicativas de nivel 2 resultaron ser todas significativas tanto estadística como empíricamente. Por ejemplo, el valor del coeficiente de la variable Jornada Completa indica que las instituciones educativas que ofrecen jornada completa obtienen en promedio un 12,6% más puntaje en lenguaje que las instituciones que ofrecen jornada nocturna y sabatina.

Modelo	Parámetro	Estimación	Error típico	gl	t	Sig.
Puntaje Lenguaje	Intersección	3,709356	0,0135528	98,121	274,196	0
	Jornada Completa	0,126696	0,01589	276,242	7,973	0
	Jornada Mañana	0,10481	0,010035	10741,995	10,444	0
	Jornada Tarde	0,101565	0,010134	10734,155	10,022	0
Puntaje Matemáticas	Intersección	3,618309	0,022562	81,916	160,37	0
	Jornada Completa	0,243559	0,021891	443,49	11,126	0
	Jornada Mañana	0,182783	0,013005	11051,216	14,055	0
	Jornada Tarde	0,197169	0,013133	11035,358	15,013	0,016
	Ratio estu./prof.	-0,001254	0,00052	1067,251	-2,415	0,016

El cuadro N. 4, también describe el modelo RMR utilizando como variable dependiente el logaritmo del rendimiento en matemáticas. Las instituciones educativas que ofrecen jornada completa obtienen en promedio un 24,35% más puntaje en matemáticas que aquellas instituciones que ofrecen jornada nocturna o sabatina. Del mismo modo el ratio estudiante/profesor de matemáticas se relaciona negativamente con el rendimiento en matemáticas, un estudiante adicional por clase de matemáticas disminuye el puntaje promedio por institución en 0,125%.

Modelo	Parámetro		Estimación	Error típico	Wald Z	Sig.
Puntaje Lenguaje	Residuos	Varianza	0,025734	0,000344	74,732	0
	InstituciónEducativa		0,001698	0,000541	3,137	0,002
Puntaje Matemáticas	Residuos	Varianza	0,043026	0,000576	74,722	0
	InstituciónEducativa		0,004817	0,001572	3,064	0,002

El cuadro N, 5 muestra las estimaciones de los parámetros de covarianza. En el modelo de lenguaje, la estimación de la varianza de los residuos (0,02573) es similar a la obtenida en el modelo nulo (0,02599); por lo tanto, no parece que la variabilidad de nivel 1 se vea afectada por la presencia de la variable tipo de jornada académica. Del mismo modo la variabilidad entre los colegios tampoco ha sufrido grandes variaciones paso de 0,001725 en el modelo AEA a 0,001698 en el modelo RMR, por lo tanto, la variabilidad del nivel 2 se ha visto afectada, pero en menor proporción por la presencia del tipo de jornada de cada institución educativa. El nivel crítico asociado al estadístico de Waid (Sig,=0,002) indica que después de controlar por el conjunto de variables de nivel 2, se rechaza la hipótesis nula de que la variación en los puntaje promedio entre colegios es igual a cero.

Para el caso de matemáticas, la estimación de la varianza de los residuos (0,043026) varía relativamente poco en relación con la obtenida en el modelo nulo (0,043951), por lo tanto, no parece que la variabilidad de nivel 1 se vea afectada por la presencia de las variables que indican la jornada académica y el ratio estudiante/profesor. Por otro lado, la estimación de la variabilidad entre los colegios pasó de 0,003753 en el modelo nulo a 0,004817 en el modelo RMR, esta variación permite concluir que la variabilidad de nivel 2 se vio ligeramente afectada por la inclusión de las variables de nivel 2. El nivel crítico asociado al estadístico de Waid (Sig,=0,001), indica que después de controlar por las variables de nivel dos, los colegios difieran en el rendimiento promedio de matemáticas. De nuevo se observa que el efecto colegio en mayor en matemáticas que en lenguaje.

Si se comparan los estadísticos -2LL se concluye que la varianza entre los colegios es distinta de cero, pues tanto el -2LL de lenguaje (-9101,206) como de matemáticas (-3325,728) es menor al -2LL del modelo nulo, por lo que se concluye que el ajuste global de los dos modelos mejoró con la incorporación de las variables de nivel 2.

El CCI del modelo RMR para el rendimiento en lenguaje asciende a 6,24%, mientras que para el modelo de matemáticas llega a 10,06%. Esta variación fue mayor, de nuevo, en matemáticas. Comparando las estimaciones de los parámetros de covarianza del modelo nulo y del modelo RMR puede conocerse la proporción de varianza explicada en el nivel 2. De esta forma, el 28,25% y el 1,56% en matemáticas y lenguaje respectivamente, de las diferencias observadas entre los colegios son atribuibles a las variables que indican la jornada académica de las instituciones educativas y al ratio estudiante/profesor de matemáticas (variables de nivel 2).

El desarrollo de la metodología propone ahora determinar que parte de la variabilidad intracentro (variabilidad de nivel 1) puede ser explicada por las variables de nivel 1 que se agregaron al modelo. Para resolver esto, es necesario obtener una ecuación de regresión para cada colegio y analizar como varían las intercepciones y las pendientes de esas ecuaciones. Al proceder de esta manera, se asume no solo que los colegios pueden diferir en el rendimiento académico promedio, sino también que la relación entre el rendimiento promedio y cada una de las variables de nivel 1 pueden no ser la misma en todos los colegios. Este tipo de modelos es denominado Modelo de Coeficientes Aleatorios, porque deja que la intercepción y la pendiente varíen aleatoriamente de colegio a colegio.

Después de varias estimaciones individuales y grupales incluyendo cada una de las variables independientes, con el propósito de determinar la significancia no solo estadística sino también empírica de los parámetros estimados, se construyó el modelo de lenguaje y matemáticas con las variables de nivel 1 que resultaron tener significancia estadística y empírica.

Modelo	Parámetro	Estimación	Error típico	gl	t	Sig.
Modelo de Lenguaje	Intersección	3,80434	0,007873	18,166	483,21	0
	Presen_ Prueba	0,03234	0,005207	11,087	6,211	0
	estutrabaja	-0,027395	0,00824	17,971	-3,325	0,004
	internetHog	0,012964	0,003671	19,349	3,532	0,002
Modelo de Matemáticas	Intersección	3,747666	0,012056	21,306	310,855	0
	Presen_ Prueba	0,049986	0,007007	12,78	7,133	0
	genero	0,056901	0,012431	21,088	4,577	0
	EP_terciaria	0,045072	0,010188	11,05	4,424	0,001

El cuadro N. 6 ofrece las estimaciones de los parámetros fijos de ambos modelos. El valor de los coeficientes asociados a las variables independientes agregadas son todos estadísticamente significativos. En la primera parte se evidencia que el coeficiente de la variable presento la prueba, indica que los estudiantes que presentaron la prueba previamente obtienen un 3,23% más de puntaje en lenguaje con respecto a quienes no presentaron la prueba antes. El estadístico y su nivel crítico (Sig.=0,000) permiten afirmar que el coeficiente es significativamente distinto de cero. Del mismo modo, los estudiantes que trabajan obtienen en promedio un puntaje menor (un 2,73% menor) que los estudiantes que no trabajan.

En la segunda parte del cuadro N. 6 se muestran los resultados del modelo del rendimiento en matemáticas. Los hombres obtienen en promedio un 5,7% más de puntaje en matemáticas que las mujeres. Mientras que los estudiantes con padres de nivel de educación terciaria obtienen en promedio 4,5% más de puntaje que los estudiantes con padres sin educación formal.

Las estimaciones de los parámetros de covarianza para los dos modelos, muestran que la varianza estimada de los residuos del modelo de lenguaje y de matemáticas es _^2 es 0,025592 y 0,04210, respectivamente, en ambos casos inferior a la obtenida en el modelo nulo. Al obtener la proporción de la varianza explicada en el nivel 1 de lenguaje (0,0153) y matemáticas (0,04211), se puede concluir que al incluir variables de nivel 1 en el modelo de regresión utilizando una ecuación separada para cada colegio, la variabilidad intracentro se reduce aproximadamente 1,53% y 4,21%, respectivamente.

La varianza de las medias o intercepciones, o variación entre las medias de las instituciones educativas resultaron ser significativas; esto indica que el rendimiento promedio de las instituciones educativas tanto en lenguaje como en matemáticas no es igual en todos los colegios.

La varianza de las pendientes de ambos modelos resultó ser no significativas, por lo tanto, no se puede concluir que las pendientes de las ecuaciones de regresión son diferentes en todos los colegios. Por otro lado, la covarianza entre las medias y las pendientes de ambos modelos para todas las variables de nivel 1 consideradas en las estimaciones, resultaron ser no significativas, por lo tanto, se concluye que las pendientes no parecen estar relacionadas con las medias. De la aplicación de este modelo, se concluye que la incorporación de las variables de nivel 1 afecta realmente poco la variabilidad de nivel 1, siendo mayor en el modelo que utiliza el rendimiento en matemáticas como variable dependiente. De este modo, pueden existir otras variables características del estudiante que no fueron consideradas en estos modelos y que pueden afectar en mayor proporción el rendimiento académico.

Habiendo encontrado que la medias (las constantes e intercepciones) varía entre los colegios, el paso a seguir es averiguar que variables o que interacción de variables de distinto nivel podrían dar cuenta de esta variabilidad. Esto se averigua con la aplicación del último modelo análisis de regresión: medias y pendientes como resultados (RMPR). De esta forma, se estiman los modelos finales de lenguaje y matemáticas, que incluyen variables de nivel 1 y 2, así como variables que indiquen interacciones entre los dos niveles.

Después de una secuencia de estimaciones, en donde se excluyeron las variables que no presentaban significancia estadística y empírica, se estimó el modelo final para cada una de las áreas evaluadas; las ecuaciones 4 y 5 muestra la estimación de los parámetros del modelo final para lenguaje y matemáticas. La omisión de algunas variables que resultaron ser no significativas, no afectaron la bondad del ajuste, pues el estadísticos -2LL se mantuvo en -9120,13 para el caso de lenguaje, y -3549,053 para matemáticas.

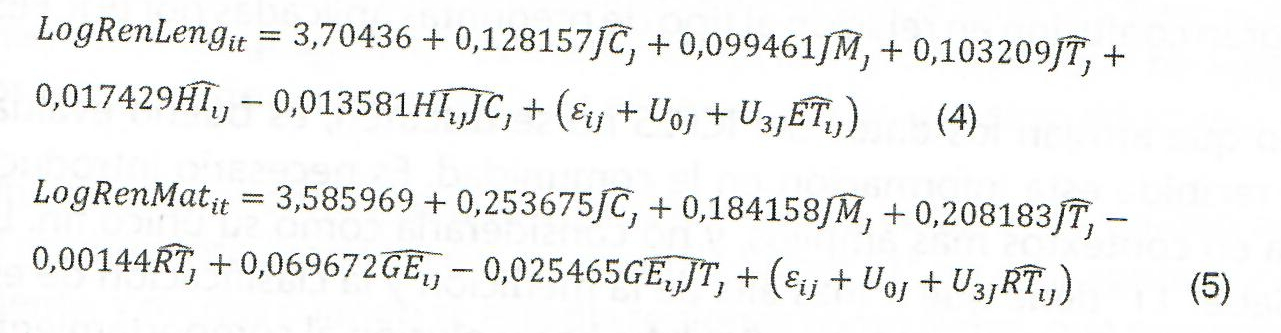
Las variables indicativas de la jornada académica (variables de nivel 2) junto con la variable internet en el hogar, y la interacción con la jornada académica tarde (variable de nivel 1) hacen parte del modelo final que incluye al rendimiento en lenguaje como variable independiente. Por el lado de matemáticas, las variables indicativas de la jornada académica, así como el ratio estudiante/profesor de matemáticas (variables de nivel 2) y el género, junto con la interacción entre la jornada tarde y el género del estudiante (variables de nivel 1), integran el modelo multinivel de matemáticas. Estas dos ecuaciones representan los modelos multinivel finales tanto de lenguaje como de matemáticas.

Al comparar el modelo nulo con el actual, se observa que la incorporación de las variables de nivel 2 incrementaron las varianza de las medias entre los colegios tanto en el rendimiento de lenguaje (20,92%) como de matemáticas (34,1%); es decir, las variables de nivel 2 agregadas, explican el 20,92% y el 34,1% de las diferencias en el rendimiento de lenguaje y matemáticas entre los colegios, Es evidente que el factor colegio tiene mayor peso sobre el rendimiento de matemáticas que sobre el rendimiento de leguaje.

El CCI aumento levemente con respecto al registrado en el modelo de medias como resultado; para el modelo de lenguaje el CCI alcanzó un valor de 4,82% mientras que para el modelo de matemáticas dicho valor ascendió a 10,08%. Esto indica que el 10,08% de la variabilidad total es atribuible a las diferencias entre las medias y/o rendimiento promedio en matemáticas de las instituciones educativas.

CONCLUSIONES

El desarrollo de la presente investigación, permite formular las siguientes conclusiones:

Del análisis etnográfico se deriva que los agentes entrevistados presentan un alto grado de desconocimiento y desinformación respecto a la calidad educativa, el rendimiento académico y las pruebas Saber 11°, pues los agentes que tienen que ver con la educación regional presentan una limitada percepción acerca del concepto de calidad educativa, en general se evidencia un total desconocimiento respecto a la intencionalidad y estructura de la prueba Saber 11° y un gran confusión en relación al tipo de preguntas aplicadas por el ICFES.

Si bien, lo que arrojan los datos del ICFES no se discuten, es bueno evaluar como es recibida esta información en la comunidad. Es necesario introducir la prueba en contextos más amplios, y no considerarla como su único fin. La prueba Saber 11° tiene que ir más allá de la medición y la clasificación de estudiantes, docentes e instituciones. Se debe hacer alusión al comportamiento del sujeto en un orden social dado, en donde se incluyan la formación, apropiación e internalización de valores. Se debe sacar la prueba de esa concepción esencialmente disciplinaria, en donde predomina una posición epistemológica muy distinta a la interdisciplinariedad, la transversalidad y la integralidad, elementos determinantes en los procesos educativos más complejos.

Tanto la escuela como las características propias del individuo determinan el rendimiento académico de los estudiantes. El factor escuela tiene mayor peso que el factor estudiante, tanto en matemáticas como en lenguaje; esto se presenta porque al analizar los estudiantes de las instituciones de educación pública de la ciudad de Neiva, caracterizados por tener bajos niveles de desarrollo socioeconómico, y por no presentar grandes diferencias entre las instituciones, el factor estudiante (la casa, los padres, etc.) difiere poco entre los alumnos, por lo tanto el factor escuela es el que registra mayor variabilidad. De esta forma, al presentar pocas diferencias en las características económicas y sociales de los estudiantes, el factor escuela es quien determina en mayor proporción las diferencias en el rendimiento académico.

La situación socioeconómica del estudiante no afecta el rendimiento académico; esto resulta lógico, pues como se mostró en el planteamiento del problema, las características socioeconómicas de los estudiantes de las instituciones de educación públicas de Neiva, no difieren mucho entre ellos, por tanto, no afecta el rendimiento académico de los estudiantes.

La educación de los padres sin duda afecta el rendimiento académico de los estudiantes; las diferencias en el nivel educativo de los padres no son tan importante en el rendimiento de lenguaje, pero sí en el rendimiento de matemáticas, en donde un mayor nivel académico del padre o la madre, garantiza un mayor logro escolar. Del mismo modo, las clases con menor número de estudiantes favorece el rendimiento académico de matemáticas. En la medida que el profesor puede atender de manera personalizada a los estudiantes, la probabilidad de que el estudiante capte mejor los conceptos es mayor. Los estudiantes de género masculino presentan mayores rendimientos en matemáticas que los estudiantes de género femenino. Esto no ocurre con el rendimiento en lenguaje, en donde tanto hombres como mujeres registran el mismo resultado académico. El acceso a las tecnologías en especial al internet, favorece el rendimiento en lenguaje. Este resultado refleja la importancia que ha adquirido en los últimos años la tecnología en el desarrollo del proceso educativo.

Finalmente, se concluye que la problemática a cerca de la calidad educativa, el rendimiento académico y las pruebas Saber 11° no está agotada completamente, y menos cuando se estudia regiones como Neiva, que presentan tantas desigualdades económicas y sociales. Está es apenas un primero estudio que debe servir de base para futuras investigaciones sobre el tema, que tiendan a contribuir en la solución del problema planteado.

Referencias bibliográficas

Aguerrondo, I. (1993). La calidad de la educación: ejes para su definición y evaluación. La Educación N° 116, p. 561-578.

Caro, B. L. (200). Factores asociados al logro académico de los alumnos de 3o y 5o de primaria de Bogotá. Coyuntura Social. No. 22, mayo. Fedesarrollo, 65-80.

Chica, S. M., Galvis, D. M., & Ramírez Hassan, A (2010). Determinantes del Rendimiento Académico en Colombia. Revista Universidad EAFIT. Vol. 46. No 160,48-72.

Coleman, J. (1966). Equality of educational opportunity. Washington; US Government Printing Office. Fertig, M., & Schmidt, M. C. (2002). The Role of Background Factors for Reading Uteracy: Straight National Scores in the PISA 2000 Study. Documentoparadis- cusión 545, Institute for the Study of Labor (IZA), Bonn.

Fuchs, T., &Woessmann, L. (2005). What Accounts for International Differences in Student Performance? A Re-ExaminationUsing PISA Data. EmpiricalEconomics32, 433-464.

Gavira, A., & Barrientos, J. (2001). Determinantes de la calidad de la educación en Colombia, de Economía. No. 159 Departamento Nacional de Planeación.

González, P, Mizala, A., & Romaguera, R (2004). Vouchers, Inequalitiesand the Chilean Experience. National Center for the Study of Privatisation in Education, Nueva York.

Hanushek, E A. (1986). The economics of Schooling. Journal of Economic Literature, vol. 24, núm.3, 1141-1171.

Hepp, P. K., Hinostoza, E., Laval, E., & Rehbein, L. (2004). Technology in Schools: Education, ICT, and the Knowledge Society. Human Development Network, Banco Mundial, Washington, DC.

López Jiménez, N., & Puentes, A. V. (2008). Acerca de la Problemática de la Evaluación de la Calidad de la Educación en Colombia. Entornos N. 21 Universidad Surcolombiana, 9-20.

López Jiménez, N., & Puentes, A. V. (2011). Evaluación de la Calidad de la Educación en Colombia. Estado del Arte. Segunda Fase. Neiva: Editorial Universidad Surcolombiana, Grupo de Investigación PACA.

López Jiménez, N., Mantilla, M., & et al. (1995). Currículo y Calidad de la Educación Superior en Colombia. Bogotá D.C.: Colciencias-ICFES.

Murillo Torrecilla, J. (1999). Los Modelos Jerárquicos Lineales aplicados a la Investigación sobre Eficacia Escolar. Revista de Investigación Educativa, 17(2), 453-460.

Piñeros, L. A., & Rodríguez, A. (1999). Los insumos escolares en la educación secundaria y su efecto sobre el rendimiento académico de los estudiantes: un estudio en Colombia. LCSHD Paper Series No. 36. World Bank Human Development.

Sanders W, & Rivers, J. (1996)-Cumulative and Residual Effects of Teachers en Future Student Academic Achievement.University of Tennessee, Valué-Added Research and Assessment Center, Knoxville,TN.

Vegas, E., & Petrow, J. (2008). Incrementar el Aprendizaje Estudiantil en América Latina. Washington D.C.: Banco Mundial.

---