Resumen: Durante el transcurso de los procesos de enseñanza-aprendizaje de los seres humanos, las matemáticas desempeñan un papel significativo en su vida cotidiana, les permite orientarse, realizar apreciaciones sobre formas y distancias, o calcular la distribución de objetos en el espacio. Considerando el aprendizaje como un proceso diario de construcción de conocimientos, la enseñanza tendrá como objetivo orientar dicho proceso. En ese sentido, el presente trabajo expuso una estrategia pedagógica que permitió que la enseñanza-aprendizaje de la matemática aplicada en geometría plana y expresiones algebraicas, pasaran de ser una temática más, a cautivar al aprendiz en la comprensión de las formas que ofrece la naturaleza. Desde esta realidad, el objetivo de esta investigación fue diseñar e implementar estrategias apoyadas en herramientas de plataformas robóticas para el mejoramiento de las competencias matemáticas en estudiantes de octavo grado de la Tecnoacademia de Neiva, teniendo en cuenta la Teoría de las Inteligencias Múltiples de Gardner y el Aprendizaje Significativo de Ausubel y Vygotsky. La metodología fue de enfoque cuantitativo, seleccionando 36 estudiantes como grupo experimental en dos momentos, donde se pusieron en práctica herramientas robóticas para la enseñanza de las matemáticas, validando la efectividad de dicha estrategia recurriendo a la prueba estadística de Rangos de Wilcoxon. Como resultados se obtuvo el diseño de dos robots que permiten en los aprendices facilitar e incrementar el mejoramiento significativo en resolución de problemas de área, perímetro, expresiones algebraicas e inferir que la planificación de estrategias pedagógicas son determinantes en el desarrollo cognitivo de los estudiantes en un ambiente de formación.

Palabras clave: enseñanza-aprendizaje, matemáticas, pedagogía, robótica, tecnoacademia.

Abstract: During the teaching-learning process of human beings, mathematics play a significant role in their daily lives, allows them to orient, make judgments about shapes and distances, or calculate the distribution of objects in space. Considering learning as a daily process of building knowledge, teaching will aim to guide the process. In that sense, this paper presented a pedagogical strategy that allowed the teaching-learning of applied mathematics in plane geometry and algebraic expressions, move to be from a simple thematic, to engage the learner in understanding the ways that nature offers. From this view, the aim of this research was to design and implement strategies supported on robotics platforms tools to improve math skills among eighth grade students at Tecnoacademia from Neiva, considering the theory of Multiple Intelligences by Gardner and Meaningful Learning of Ausubel and Vygotsky. The methodology was of quantitative approach, selecting 36 students as experimental group at two points. It was implemented robotic tools for teaching mathematics. Likewise, it was validated the effectiveness of this strategy using the statistical test of Wilcoxon Rank. As a result, it was obtained the design of two robots that allow for learners to facilitate and increase the significant improvement in problem solving about area, perimeter, algebraic expressions and also infer that the planning of teaching strategies are crucial to cognitive development of students in a training environment.

Keywords: teaching-learning, mathematics, pedagogics, robotics, tecnoacademia.

Introducción

La enseñanza de las matemáticas en su práctica pedagógica se rige bajo los parámetros que establece el Ministerio de Educación Nacional (MEN, 1998), los cuales se apartan de las necesidades específicas de cada región en sus diferentes contextos educativos.

A través del tiempo, las matemáticas se desarrollan como el eje central en los procesos de enseñanza-aprendizaje de los estudiantes. Alrededor de ella se desenlazan metodologías y estrategias que generan conocimiento científico, al tiempo que desarrollan la comprensión en cálculos aritméticos, permitiendo así el progreso social, cultural y científico en la solución de problemas que impliquen la aplicación de dichos conocimientos adquiridos a través del razonamiento lógico en las actividades cotidianas de los estudiantes.

En la región la necesidad de implementar estrategias pedagógicas para el fortalecimiento del aprendizaje en áreas como las ciencias básicas y, en particular, las matemáticas, se hace evidente cuando se encuentran deficiencias en el aprendizaje, lo que implica desarrollar las habilidades de los educandos que en ocasiones están directamente relacionadas con el mundo en el que viven; es en estos espacios donde es posible la aplicación de estrategias diferentes que evidencien empíricamente la calidad en una mejor asimilación de cualquier tema que forme parte de las actividades tendientes al logro de los objetivos y metas propuestas en el currículo de cada institución educativa; de esta forma se busca aplicar, desde la Tecnoacademia de Neiva, estrategias didácticas para el mejoramiento en el área de matemáticas fundamentadas a partir de herramientas en plataformas robóticas.

Tecnoacademia es una línea programática del SENA; nació en el país en 2008 como un escenario de aprendizaje dotado de tecnologías emergentes para desarrollar competencias encaminadas a la innovación, a través de la orientación por proyectos de formación y/o investigación aplicada, para optimizar el conocimiento útil que habilite en el aprendiz su capacidad para el mundo del trabajo con soluciones innovadoras para las empresas y los sectores productivos (SENA, 2010).

En Neiva, la Tecnoacademia está adscrita al Centro de la Industria, la Empresa y los Servicios de la Regional Huila; los estudiantes de grado octavo hacen parte de los procesos de formación al unirse en el llamado que se realiza en las instituciones educativas para participar en contra jornada al horario de clases habitual en la línea que prefieran, según su vocación. Nanotecnología, Biotecnología, Ingeniería y Diseño, Ingeniería TIC y Ciencias Básicas en áreas específicas como Matemática Aplicada, Física Aplicada y Química Aplicada, son las opciones para que los aprendices disfruten de un espacio en el que se les incentiva por la investigación en ciencia, de tal forma que se privilegie la aplicación del conocimiento para resolver problemáticas cotidianas, y es desde este proceso de formación con los estudiantes de Neiva, donde se espera fomentar y fundamentar el aprendizaje por el área de las matemáticas.

En el aprendizaje de las matemáticas que perciben los estudiantes en la capital del Huila se demuestran grandes falencias que se ven reflejadas en pruebas Icfes o Saber Pro, que realizan anualmente las instituciones educativas (Icfes, 2016).

Desde la Tecnoacademia se evidencia que los estudiantes, en el momento que se inscriben para iniciar su proceso de formación, no demuestran interés por hacer parte de los cursos de matemáticas: consideran que son difíciles, aburridos y sin importancia; desde esta realidad se pretende promover el aprendizaje y aplicar los conocimientos de las matemáticas apoyados en áreas que a los educandos les parecen atractivas, como la robótica. Construir un robot les despierta la curiosidad y les permite explorar sus capacidades. Se espera entonces, de acuerdo con esta perspectiva, enseñar matemática aplicada a la robótica.

1. Marco Teórico

Desde las primeras civilizaciones, el uso de las matemáticas ha estado presente en la generación de conocimiento científico, avances tecnológicos y progreso en general, como un prerrequisito necesario para acceder a mayores niveles de calidad de vida. En todas las actividades cotidianas de la gran mayoría de personas en el mundo, las matemáticas tienen un protagonismo excepcional, desde una simple cuenta o suma para comprar alimentos, hasta la solución de complejas ecuaciones para determinar condiciones ambientales en planetas distantes, entre otras (Viloria & Godoy, 2010), (Benedito, 2000).

No es secreto que el estudio de las matemáticas requiere concentración y dedicación; no obstante, se ha creado un prejuicio que las define como una materia complicada y difícil, que los únicos que sobresalen en su entendimiento deben considerarse como ‘nerds’ o ‘superdotados’, muchas veces tildados de locos (Ausubel D., 1998).

Constantemente se realizan investigaciones con el fin de proponer nuevas herramientas que aporten en el mejoramiento de la asimilación de los conceptos matemáticos. No obstante, el panorama no es alentador y siguen presentándose bajos resultados en las pruebas sobre esta área, como lo demuestra el Informe del Programa Internacional para la Evaluación de Estudiantes PISA, cuyo objetivo es el análisis del rendimiento a través de la formulación de exámenes que se aplicaron cada tres años. En el año 2012 se realizó en 65 países de los cinco continentes, incluyendo los 34 que pertenecen a la OCDE, para determinar la valoración internacional académica de los estudiantes en diferentes áreas de conocimiento, en las cuales en nuestra nación se evidencian resultados bajos en relación con otros países, aunque en los últimos años se mostró una leve mejoría en relación con las pruebas pasadas; no obstante, el promedio nacional para Colombia es deficiente con respecto a otros países (OCDE, 2013).

La estrategia fue fundamentada en el enfoque teórico de Gardner, con su aporte referido a las inteligencias múltiples, donde se identifican ocho formas diferentes de inteligencia que se desarrollan para aprender (Gardner, 1983). Para el desarrollo del proyecto se seleccionaron la Inteligencia Múltiple, lógico matemática y la corpóreo-kinestésica. Lógico matemático se considera una de las principales áreas del conocimiento básico y fundamental, por lo que se ha definido como una de las más destacadas áreas en conjunto con el aprendizaje del lenguaje; todos los desarrollos y diseños de currículo deben contemplar las matemáticas en uno de sus ejes principales (Morin, 2008).

La matemática aplicada es particularmente el uso específico de herramientas matemáticas adaptadas a procesos y actividades de diferentes ciencias, acuñándoles nombres y definiciones; técnicas que hacen parte del uso del lenguaje científico que se desarrolla en las diferentes profesiones y áreas del conocimiento como, por ejemplo, economía matemática, biomatemáticas, matemática financiera o matemáticas para ingenieros, entre otras.

La importancia de las matemáticas en el desarrollo académico de los escolares, y previendo que en el proceso de aprendizaje de ellas se necesita una acumulación de conocimientos básicos que poco a poco se han transformado en procesos más elaborados, hace necesario que las bases teóricas y prácticas sean asimiladas de la mejor manera por los escolares, de acuerdo a su maduración y avance intelectual (Markarian, 2002). Los niveles generales de desempeño en el área de matemáticas en Colombia dan evidencia de grandes variaciones, falta de constancia, evolución progresiva y creciente volatilidad en los desempeños.

Por estas razones se propone la aplicación de una estrategia didáctica implementando la robótica que sirva de apoyo para mejorar el aprendizaje en el área de matemáticas, con participación activa en la construcción de conceptos, a través de actividades pensadas y secuenciales para el desarrollo de habilidades; la formulación y resolución de problemas. Dicha propuesta se fundamentó a partir de la teoría que indica que el aprendiz debe obtener y permitir un aprendizaje significativo según a estructura cognitiva existente en cada uno de ellos (Ausubel, 2002), (Vygotski, 1935/1984) desde la cual se motiva para iniciar los procesos que se desarrollan con la construcción de robots en proyectos de investigación aplicada.

En los ambientes de aprendizaje de la Tecnoacademia, la construcción de robots, en los proyectos de investigación son aplicados como estructuras mecánicas que operan con cierto grado de autonomía, bajo el control de una programación para realizar una tarea que dispone de un sistema sensorial diseñado para obtener información de su entorno; programación que se plantea según las necesidades del educando a través de software con un específico lenguaje de programación.

La robótica se divide en dos áreas: manipulación y móvil, que en conjunto han dado lugar a infinidad de aplicaciones en áreas muy diversas (Saavedra & Acosta Sánchez, 2005).

A partir del aprendizaje significativo se debe lograr interacción en la enseñanza de las matemáticas, para ello se implementarán plataformas robóticas en los ambientes. Para el desarrollo de esta investigación se utilizaron las plataformas VEX y Arduino para solucionar problemas del entorno.

VEX se encuentra diseñada para el aprendizaje de las áreas de las STEM (Ciencia, Tecnología, Ingeniería y Matemáticas); se convierte en un espacio donde los estudiantes logran explorar mediante la tecnología robótica, los principios científicos y de ingeniería. Además, los proyectos de robótica VEX fomentan el trabajo en equipo, el liderazgo y la capacidad de resolución de problemas, lo que hace posible que los maestros incentiven a los jóvenes teniendo en cuenta las habilidades de cada uno de sus estudiantes. “Es una de las plataformas que se está expandiendo más rápidamente, está orientada desde secundaria a laboratorios universitarios, aunque también es una plataforma óptima para los aficionados a la robótica y los amantes de las competencias” (System, 2002). En lo que refiere Arduino, es una plataforma electrónica de código abierto basado en hardware y software fácil de usar, está diseñada de tal manera que cualquier persona pueda realizar proyectos interactivos de robótica, aplicados en diferentes áreas o temáticas (Arduino, 2005).

Con las herramientas robóticas que genera el presente proyecto, se logra identificar las temáticas que los estudiantes pueden relacionar con problemáticas cotidianas; en donde se define la enseñanza-aprendizaje por la geometría en aplicaciones de área y perímetro, igualmente las aplicaciones de las expresiones algebraicas de ecuaciones lineales y cuadráticas.

Para el desarrollo del proyecto es vital la utilización de geometría para identificar las formas que se encuentran en el plano o en el espacio se utilizó específicamente la geometría plana que estudia las figuras planas, las cuales se destacan por tener dos dimensiones: largo y ancho. Comprender la geometría plana de manera más clara, requiere tener en cuenta conceptos elementales para pasar a conceptos más complejos, como por ejemplo “polígono”, región del plano limitada por tres o más segmentos, en que intervienen algunos elementos como lo son los lados, vértices, ángulos, diagonal, perímetro y área.

Por otro lado, se definen temáticas en las que intervienen las expresiones algebraicas en concepciones de ecuaciones. Según Euler define las ecuaciones como la Teoría de los "cálculos con cantidades de distintas clases", los cuales se pueden realizar con números reales; una ecuación de primer orden es aquella que tiene una incógnita, también denominada ecuación lineal, y una ecuación de segundo orden es aquella que tiene una variable con dos incógnitas. Al definir ecuación se especifica como una expresión donde su lenguaje simbólico se representa de la forma donde x es la expresión de una incógnita o variable y a,b,c son constantes; los términos están relacionados por medio de la operación adición o sustracción (Moreno & Castellano, 1997).

El presente proyecto generó dos herramientas robóticas para fortalecer el proceso de enseñanza-aprendizaje en matemáticas, específicamente en geometría plana, donde se intervienen conceptos de área y perímetro de figuras geométricas; además, temáticas de expresiones algebraicas que definen conceptos de ecuaciones lineales y cuadráticas en los estudiantes de la Tecnoacademia del SENA en Neiva, programa de enriquecimiento científico para jóvenes de bachillerato que sigue el modelo de formación por proyectos, enmarcado en el Acuerdo 009 de 2010, a través de la ejecución de proyectos de investigación e innovación aplicada, de tal forma que se privilegie la aplicación del conocimiento en los jóvenes desde temprana edad, para el desarrollo de competencias para la innovación, el emprendimiento y el mundo del trabajo, (SENA, 2016). Además, fortalecer la educación media para facilitar la movilidad de los jóvenes hacia la educación superior de nivel tecnológico y universitario.

2. Metodología

La investigación consideró el enfoque cuantitativo, descriptivo, experimental, longitudinal. Su principal objetivo estuvo dirigido a analizar y evaluar dichas estrategias pedagógicas para la enseñanza-aprendizaje de las matemáticas de los estudiantes de la Tecnoacademia.

Se determinó cuantitativo, porque está asociado a la medición de variables; descriptivo, al identificar el nivel de conocimiento de los estudiantes; además, longitudinal, porque su inicio es anterior a los hechos estudiados y los datos se recopilaron a medida que fueron sucediendo.

Para desarrollar el enfoque se realizó un análisis en dos fases. En la primera fase de datos, se identificó el nivel de conocimiento de los aprendices de la línea de Ciencias Básicas- Matemática Aplicada de la Tecnoacademia del SENA de Neiva, para así determinar las temáticas a enseñar y el diseño de dos prototipos como estrategias pedagógicas en plataforma robótica para la enseñanza de geometría y ecuaciones. En la segunda fase se evaluaron los resultados obtenidos después de aplicar la estrategia pedagógica propuesta en plataformas robóticas en los aprendices de grado octavo del curso complementario de Matemática Aplicada. Se implementó para el análisis de la información la prueba estadística de Rangos de Wilcoxon, que permite verificar si existen diferencias significativas entre las medianas de las variables en consideración, en la cual la hipótesis nula contempla igualdad entre las medianas de la calificación obtenida y la hipótesis alterna no contempla igualdad (Smits, 2011); es decir, supone que son diferentes las medianas de las calificaciones obtenidas de los temas de matemáticas desarrollados en conceptos de geometría y ecuaciones, implementada para encontrar la efectividad de la estrategia de enseñanza.

3. Resultados y Discusión

Después de realizar el procesamiento de la información de los aspectos caracterizados de los aprendices seleccionados como grupo experimental aplicando el aprendizaje significativo, teniendo en cuenta la I.M de cada uno de los participantes de la formación complementaria en matemáticas se encontró lo siguiente:

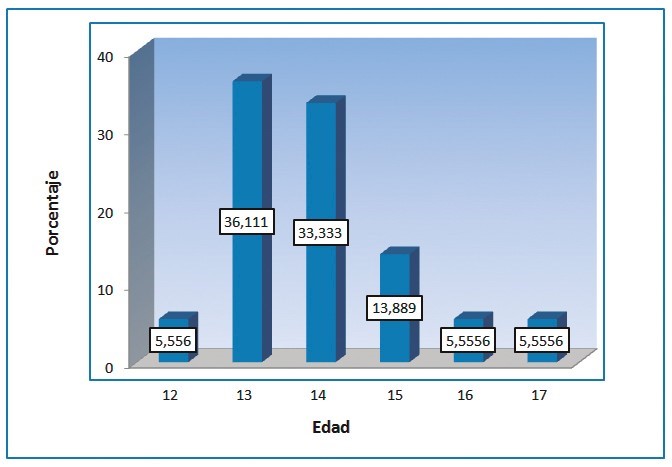
Figura 1. Edad.

Al realizar el análisis por edad se encontró que la edad promedio está entre 13 y 14 años, que permitió establecer la relación del aprendizaje y desarrollo intelectual en la edad de los estudiantes, como lo explica Vygotsky.

El diagnóstico permitió identificar el nivel de conocimiento de los aprendices de Matemática Aplicada de la Tecnoacademia SENA Neiva, caracterizando los siguientes aspectos:

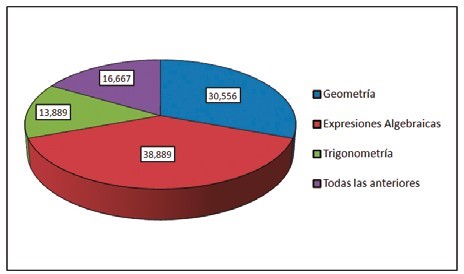
Figura 2. Porcentaje de temáticas que se dificultan en los aprendices.

La Figura 2 permitió dar un diagnóstico de las temáticas en las cuales los estudiantes tenían mayor dificultad de aprendizaje en matemáticas. 38% de los estudiantes expresan que conceptos de expresiones algebraicas son complejos; el 30% considera que la geometría, por ser tan extensa, los conceptos son difíciles de aprender y aplicarlos en el mundo que los rodea. Este diagnóstico permitió implementar el método científico en un primer momento para determinar las áreas de conocimiento en las que los estudiantes tienen falencias y dificultades a la hora de resolver problemas que se presentan en la vida cotidiana; a partir de estos resultados se construyen los conocimientos de acuerdo con la teoría de Vygotsky, que se basa en el aprendizaje sociocultural de cada individuo mediante la relación con el mundo que los rodea y su importancia en el contexto social. Para el reconocimiento de las temáticas en el primer momento se tuvo como referencia el diagnóstico realizado, del cual se infiere la baja interpretación de conceptos de ecuaciones y de geometría. Por ello se inician actividades en talleres en los cuales intervienen problemas de aplicación con dichas temáticas.

Además, se caracterizó, según el desarrollo de las Inteligencias Múltiples (I.M.) propuestas por Gardner, que los aprendices perciben su conocimiento como lo representa la siguiente Figura:

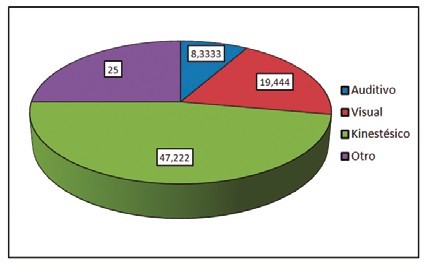
Figura 3. Caracterización de Inteligencia Múltiple desarrollada en los aprendices.

La Figura 3 representa que el 47% de los estudiantes encuestados, consideran que tienen desarrollada la I.M Kinestésica y el 25% responden “Otro” en los cuales se tuvo en cuenta en señarles mediante procedimientos lógicos matemáticos.

Teniendo en cuenta lo anterior, a los estudiantes se les facilita realizar exámenes escritos y, además, se infiere facilidad por realizar talleres.

También se identificó sí a los estudiantes les gustaría aprender matemáticas a través de la robótica. Se encontró que el 94% considera necesario implementar herramientas robóticas en un ambiente de formación que estimule y fomente un aprendizaje significativo que logre integrar la ciencia, la tecnología, la ingeniería y las matemáticas en los proyectos realizados en un momento de clase.

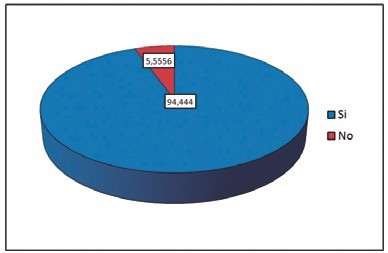
Figura 4. Porcentaje de aprendices que desean aprender matemáticas a través de la robótica.

Luego de reconocer y tener claridad en las temáticas, se inició con la construcción de dos robots implementando las plataformas robóticas VEX y Arduino, utilizadas para la creación y programación de prototipos robóticos, donde se realizó la socialización de ideas de cada uno de los aprendices de la forma o apariencia de los dos prototipos robóticos a realizar; así mismo, se seleccionan dos diseños y dos nombres para cada uno de los robots: MATROB para las temáticas de área y perímetro de las figuras geométricas, y ECUMAT para las ecuaciones matemáticas.

Se logró construir dos robots matemáticos programados para realizar cálculos geométricos y algebraicos. El diseño de las herramientas robóticas fue apoyado por la imaginación y aporte de los 36 aprendices de matemática aplicada, dando como resultado “MATROB” y “ECUMAT”.

MATROB es un prototipo robótico tipo automóvil, al que se le instalaron llantas lisas tipo vehículo particular. Los cables que transmiten la potencia a los actuadores y las señales de los sensores al microcontrolador son dispuestos de tal forma que queden ordenadas.

Figura 5. Robot “Matrob”.

Lo que permite el cálculo de área y perímetro de cualquier cuadrado, rectángulo o circunferencia que recorra y reconozca a través de sus sensores.

De otro lado, ECUMAT permite encontrar las raíces de las ecuaciones lineales y cuadráticas a través del reconocimiento de su ecuación general, haciendo que el aprendiz no memorice las fórmulas sin saber la aplicación o utilidad de dichas expresiones en problemas cotidianos.

Figura 6. Aprendices en formación.

Figura 7. Prototipo ECUMAT.

A través de los análisis estadísticos se logra comprobar que las plataformas robóticas VEX y Arduino utilizadas en un ambiente de formación generan cambios significativos en los procesos de enseñanza- aprendizaje de matemáticas.

Se realizó la prueba de Kolmogorov-Smirnov, elaborada para inferir si las variables de las calificaciones, denominadas Nota 1 (examen diagnóstico realizado en primer momento cuando los aprendices se inscriben a iniciar el curso complementario de matemáticas) y Nota 2 (examen realizado a los aprendices que recibieron formación de matemáticas con herramientas robóticas) se distribuyen o no se distribuyen normalmente.

Tabla 1

Prueba de Kolmogorov-Smirnov.

Prueba de Kolmogorov-Smirnov para una muestra		Nota1	Nota2
N	Media	36	36
Parámetros normalesa,b	Desviación	1,422	3,858
	estándar	,7702	,4087
Máximas diferencias extremas	Absoluta	,196	,279
	Positivo	,109	,279
	Negativo	-,196	-,135
Estadístico de prueba		,196	,279
Sig. asintótica (bilateral)		,001c	,000c

De la tabla 1 se logra reconocer que los datos no se distribuyen normalmente planteándose la siguiente hipótesis:

HNULA: Los datos analizados se ajustan a una distribución normal.

HALTERNA: Los datos analizados no se ajustan a una distribución normal.

Como resultado se obtuvo el p-valúe (Sig. asintótica) menor a 0,05; por lo tanto, se rechaza la hipótesis nula, es decir, se acepta la hipótesis alterna, porque el p-valúe encontrado es igual a 0,0004 en los resultados obtenidos de las variables Nota 1 y Nota 2, lo que indica que los datos no se distribuyen normalmente. Para analizar dichas variables que resultan ser no paramétricas, según la prueba de Kolmogorov-Smirnov, se aplicó la prueba de rangos de Wilcoxon por ser apropiada para hallar diferencias significativas en dos muestras dependientes o variables tomadas en diferente momento, en este caso la nota 1 y la nota 2.

Lo anterior contribuyó a la condición de analizar las variables de las calificaciones obtenidas en los dos momentos empleando la prueba estadística de Wilcoxon, la cual se toma para analizar las medianas de las calificaciones obtenidas en los dos diferentes momentos denominadas Nota1 y Nota 2.

Tabla 2

Prueba de Wilcoxon de los rangos con signo.

Rangos		N	Rango promedio	Suma de rangos
Nota 2 - Nota 1	Rangos negativos	0a	,00	,00
	Rangos positivos	36b	48,50	666,00
	Empates	0c
Total		36

Tabla 3

Estadísticos de pruebaa.

	Nota 2 - Nota 1
Z	-5,240b
Sig. asintótica (bilateral)	,0004

De las tablas 2 y 3 se identifican la Hipótesis nula H0 y la Hipótesis alterna H1 como: H0=Las medianas son iguales, por lo tanto, no hay diferencias significativas aplicando la estrategia para la enseñanza de las matemáticas.

H1= Las medianas son diferentes, por lo tanto, sí hay diferencias significativas aplicando la estrategia para la enseñanza de las matemáticas.

Se encuentra que el p-valúe es menor a 0,05; por lo tanto, se acepta la hipótesis alterna, rechazando la hipótesis nula, con la que se concluye que sí se dan diferencias significativas entre las dos notas, es decir, la planificación de estrategias pedagógicas fundamentadas con herramientas en plataformas robóticas son determinantes en el desarrollo cognitivo de los estudiantes. Enseñar a partir de herramientas robóticas como VEX y Arduino contribuyen a mejorar el aprendizaje de matemáticas, pues permite la integración de conceptos con la construcción de problemáticas del contexto real.

4. Conclusiones

Los aprendices presentan características distintas de acuerdo con su contexto y personalidad, lo que los lleva a desarrollar uno o varios tipos de inteligencia múltiple, y según sus preferencias, se construye un modelo de aprendizaje que surge a partir del conocimiento de sus necesidades y el desarrollo de sus cualidades en un ambiente de formación.

Los resultados del diagnóstico permitieron identificar los conceptos de matemáticas con los que llegan los estudiantes en el primer momento de formación; paralelamente permitió integrar los saberes de grado octavo en el que se encuentran vinculados, se reconoce que en los temas de geometría y ecuaciones tienen mayor dificultad. A partir de esta información se crearon espacios basados en la participación activa para fomentar el autoaprendizaje y el aprendizaje colaborativo desde diversas situaciones.

Así se logró visualizar, manipular activamente el proceso de enseñanza-aprendizaje, que se fundamente no sólo en un aprendizaje significativo, sino la construcción de valores, la comunicación, la aceptación de la diferencia y el trabajo en equipo.

En relación con el diseño de prototipos robóticos, se encontró que manipular este tipo de plataformas como herramientas en los ambientes de formación estimula el pensamiento lógico-matemático y creativo, propiciándoles la oportunidad de ser intérpretes de su propio aprendizaje a partir de la construcción colaborativa de los aprendices, según su contexto.

Igualmente se identificó que las plataformas empleadas VEX y Arduino, facilitaron el uso y la programación de temas de las ciencias básicas en robótica, haciendo de esto una experiencia sencilla y agradable, a su vez reduciendo el temor a las matemáticas, generando espacios de diversión, pues a través del aprendizaje de dichas plataformas los estudiantes descubren que las matemáticas se pueden aplicar para resolver problemas cotidianos, lo que los conduce a ejercitar la memoria mediante el sentido común de problemáticas cotidianas; adquirieron rapidez en los cálculos matemáticos aplicando conceptos de búsqueda de área y perímetro de figuras geométricas, y de ecuaciones lineales y cuadráticas; a su vez, consolidaron en su mayoría competencias básicas del bloque de contenido geometría, expresiones algebraicas y lograron establecer mejores relaciones de liderazgo, creatividad, amistad y solidaridad.

Los resultados obtenidos con la aplicación de la estrategia pedagógica propuesta en plataformas robóticas en los aprendices de grado octavo de la Tecnoacademia se evaluaron mediante el análisis de la prueba estadística de Rangos de Wilcoxon, que permite verificar que la aplicación de estrategias didácticas a partir de herramientas robóticas es significativamente preferente a la enseñanza con un modelo tradicional en el que no se implementen recursos diferentes en un ambiente de aprendizaje.

En general, se puede afirmar que implementar plataformas robóticas para la enseñanza de las matemáticas enriquece la adquisición de conocimientos científicos en los estudiantes; involucrar en el contexto herramientas con la manipulación de robots cambia la disposición de los educandos para el aprendizaje de las matemáticas. La enseñanza permite el desarrollo de las habilidades de pensamiento, análisis, comunicación, visualización y lectura del mundo, pero es necesario cambiar los métodos de enseñanza tradicional y abstracta, por unos métodos activos, que motiven el aprendizaje e interés por las matemáticas; además, que permita con ello la resolución de problemas en matemáticas, aplicados al mundo real desde las concepciones adquiridas en un ambiente de formación.

5. Recomendaciones

Es necesario instruir desde la educación básica secundaria conceptos de geometría y ecuaciones en la enseñanza de las matemáticas, que motiven al aprendiz a reconocer su importancia en el perfeccionamiento de habilidades y destrezas para resolver problemas de aplicación, que benefician los métodos de enseñanza-aprendizaje en diferentes áreas del conocimiento. Además, debe estar sustentada en la aplicación de estrategias innovadoras que se adapten a las tendencias actuales en esta materia, entendidas éstas como la construcción a través de las ideas que resulten luego de la observación y el razonamiento. Todos estos aspectos están relacionados con la teoría constructivista, la cual reconoce que el estudiante es partícipe en la construcción de significados asociados a su propia experiencia.

Al realizar este tipo de actividades en los ambientes de aprendizaje, se debe tener en cuenta la conformación de equipos heterogéneos, que permitan la participación y la motivación de cada uno de los miembros, para estimular el buen desempeño de trabajo colaborativo.

Al momento de implementar estrategias robóticas en los procesos de enseñanza aprendizaje, es necesario establecer una finalidad que permita construir un aprendizaje, pues si bien el uso de los computadores cuando se utilizan para la programación de los robots en la enseñanza de cualquier área, además de motivar al estudiante, también se pueden convertir en un distractor. Por ello, el maestro es el encargado de guiar al aprendiz en su práctica pedagógica, brindando un espacio donde sea el aprendiz el que construye su propio conocimiento.

Implementar la robótica como herramienta para la educación desde los primeros grados de bachillerato en las instituciones educativas genera motivación para el estudiante que se encuentra en grado octavo, pues despierta la creatividad, lo que permite desarrollar interés por áreas como las matemáticas.

Se recomienda constituir semilleros de estudiantes de matemática que lideren los procesos de crear, diseñar e implementar estrategias que desarrollen la matemática de manera interactiva, para que las estrategias sean efectivas, que brinden una interacción significativa con otros estudiantes. Vincular al estudiante con experiencias de aprendizaje a partir de otros en clases permite incentivar interés por los aprendices que no se sienten motivados.

En el diseño e implementación de estrategias constructivistas para el aprendizaje de las matemáticas, el maestro debe tener en cuenta que esta disciplina constituye uno de los ejes fundamentales sobre los que se sostiene la formación de los estudiantes, no solo porque a través del tiempo se da gran importancia en los niveles educativos como lo referencia el MEN, sino también porque su aprendizaje contribuye significativamente al desarrollo del pensamiento lógico y la relación con el mundo que los rodea.

Revista Paca 9, Diciembre 2019, ISSN 2027-257X