Resumen: ¿Qué sucede con la Autoevaluación Institucional en los establecimientos educativos del sector oficial? ¿Existe una cultura de la autoevaluación en las instituciones educativas? ¿Es hora de resignificar la Autoevaluación Institucional?

Para caracterizar las prácticas evaluativas del profesor de matemáticas se identificó la tipología sugerida por Zambrano (2014), y para el diseño metodológico el Análisis Didáctico desde la perspectiva de Gómez (2015), que promoviera buenas prácticas evaluativas. Este referente aportó información relevante desde la didáctica de las matemáticas, las matemáticas mismas y el contexto para el diseño de las tareas matemáticas. Como producto final de esta investigación se tiene como resultado cinco tareas que buscan mejorar las prácticas evaluativas, utilizando el análisis didáctico. La propuesta de evaluación presentada motiva los intereses de los estudiantes, y busca generar escenarios de reflexión acerca de lo que están aprendiendo los estudiantes, cómo lo está aprendiendo y cuál es la responsabilidad del profesor en el diseño e implementación de estrategias de aula que permitan que los estudiantes se acerquen a los aprendizajes y capacidades.

Palabras clave: prácticas evaluativas, análisis didáctico y buenas prácticas.

Abstract: The document shows the results of the research project entitled “Understanding the evaluative practices of the mathematics teacher to improve the learning of the linear function”, defining the purposes of characterizing the evaluative practices carried out by the mathematics teacher associated with the mathematical content linear function, identifying from the curricular model Didactic Analysis good evaluative practices and propose a methodological strategy to promote good evaluation practices that contribute to the improvement in the understanding of the linear function in the mathematics classroom.

To characterize the evaluative practices of the mathematics teacher, the typology suggested by Zambrano (2014) was identified and for the methodological design the Didactic Analysis from the perspective of Gómez (2015), which promoted good evaluative practices, this reference provided relevant information from the didactics of mathematics, mathematics itself and the context for the design of mathematical tasks.

Keywords: evaluative practices, didactic analysis, good practices.

Introducción

La pregunta que guió la investigación presentada fue: ¿Cómo promover buenas prácticas de evaluación que aporten al mejoramiento en el aprendizaje de la función lineal?. Para su desarrollo se planteó como propósito comprender las prácticas evaluativas del profesor de matemáticas con el fin de promover buenas prácticas de evaluación para el aprendizaje de la función lineal. En el marco de los intereses investigativos, las categorías conceptuales que se abordaron para su sustento teórico corresponden a los siguientes referentes: Evaluación: Popham (1990); Castillo y Cabrerizo (2003) y Zambrano (2014). Tipos de evaluación: Stenhouse (1984), Bordas y Cabrera (2001), Stiggins (2002), Eisner (2002), Litwin (2005), Freire (2002), Carr (2005) Moreno y Ortíz (2008), Flores y Gómez (2009), y Zambrano (2014). La evaluación de los aprendizajes en matemáticas: Chevellard (1991) y Rico (1997). Las buenas prácticas: González (2001), Epper y Bates (2004); Escudero, Gonzáles y Martínez (2009); De Pablos, Colás y González (2010) y Boza y Toscano (2011). El análisis didáctico como modelo curricular para promover buenas prácticas evaluativas: Rico (1997); Gómez (2006-2015); Cañadas, Gómez y Pinzón (2015) y Hurtado, Ochoa y Triviño (2017); y la función lineal como contenido matemático escolar: Lineamientos Curriculares para el área de Matemáticas (1998); Estándares Curriculares en Matemáticas (1997) y Derechos Básicos de Aprendizaje (2016).

En virtud a los elementos que fundamentan el referente teórico y a los intereses de la investigación, esta se sustentó en una perspectiva interpretativa y crítica de las ciencias sociales, asociada a los métodos cualitativos de la investigación social (Kemmis y Carr, 1986), los cuales reivindican la dimensión subjetiva de las prácticas investigativas en el aula de matemáticas.

Respecto a sus resultados, el proyecto permitió describir las prácticas evaluativas que ponen en funcionamiento los profesores en el aula de matemáticas, asociadas a la función lineal, identificadas desde el modelo curricular “Análisis Didáctico”, buenas prácticas evaluativas asociadas al contenido a partir del reconocimiento de su diversidad de significados, formas de representación y los fenómenos que le dan sentido. Finalmente, el proyecto aportó una construcción metodológica para favorecer buenas prácticas evaluativas asociadas a la función lineal, desde el diseño de cinco tareas de aprendizaje, sustentadas desde el modelo curricular.

Los resultados de la investigación contribuyen a la educación matemática, aportando una propuesta metodológica innovadora que promueve mejoras en las prácticas evaluativas del profesor de matemáticas en el aula referidas al contenido función lineal, reconociendo desde las mismas matemáticas y el contexto, información útil y necesaria para su comprensión.

Referentes teóricos

Teniendo en cuenta los intereses de la investigación, las categorías conceptuales que la sustentan son: la evaluación, tipos de evaluación, la evaluación de los aprendizajes en matemáticas, las buenas prácticas, el análisis didáctico como modelo curricular para promover buenas prácticas evaluativas y la función lineal como contenido matemático escolar.

Respecto a la evaluación, Freire (2002) y Carr (2005) señalan que la evaluación simboliza el sendero que permite en los estudiantes el desarrollo de sus habilidades cognitivas y sociales, que los convertirán en seres autónomos y conscientes de sus responsabilidades sociales. Las prácticas evaluativas del profesor no deben sustentarse en la medición del conocimiento, sino en la promoción de competencias y habilidades para que los estudiantes se acerquen a las formas de pensar y resolver problemas que les permitan comprender el mundo en que habitan.

coherencia a la perspectiva de Freire y Carr, Chevellar (1991), refiriéndose a la evaluación del aprendizaje de las matemáticas, señala que esta hace parte del funcionamiento didáctico en la relación de la tríada profesor, saber matemático y estudiante. La evaluación es parte del contrato didáctico, lo cual hace que no se convierta en una acción periférica del proceso didáctico, sino que hace parte de las reglas, las estrategias y los procesos de enseñanza, de aprendizaje y de comunicación.

En cuanto a las buenas prácticas, Escudero, Gonzáles, y Martínez (2009) señalan que la buena práctica no debe entenderse como algo objetivo, fijo o predeterminado y externo a la acción de los sujetos y sus contextos; requiere, más bien, ser construída a través de procesos juiciosos y propósitos morales situados en contextos, procesos que han de implicar reflexión e interpretación por parte de los actores y procesos que al mismo tiempo han de quedar expuestos a ser contrastados y validados en la acción debidamente fundada, no separados de ella. Los autores enfatizan que desde esta concepción, una buena práctica se entiende como un empeño reflexivo, interpretativo, dialogado y personal, también social y cultural.

Finalmente, Gómez (2006) identifica el Análisis Didáctico como una herramienta útil para el diseño de currículos locales (diseño de una clase de matemáticas) y se estructura alrededor de los organizadores del currículo. Estos últimos, según Rico (1997), se definen como elementos conceptuales y metodológicos que posibilitan al profesor la recolección, organización y selección de información acerca de los diferentes significados de los objetos matemáticos. El Análisis Didáctico como modelo curricular implica procesos de reflexión y análisis de las matemáticas, su enseñanza y su aprendizaje; este incorpora cuatro tipos de análisis que se sustentan desde los componentes curriculares: contenido (análisis de contenido), objetivos (análisis cognitivo), metodología (análisis de la instrucción) y evaluación (análisis de la actuación). Los tres primeros análisis se ocupan del diseño, mientras que el análisis de actuación se centra en la puesta en práctica, implementación y la posterior evaluación de los resultados obtenidos.

Metodología

La investigación se inscribe en un enfoque de investigación cualitativa, exploratoria y transformadora. Su carácter cualitativo se sustenta en que centra su interés en comprender las prácticas evaluativas que realiza el profesor de matemáticas; es de carácter exploratorio porque constituye un acercamiento a los escenarios del aula de clase de matemáticas para caracterizar las prácticas evaluativas que realiza el profesor, asociadas a la función lineal; y es de carácter transformador, porque su reconocimiento crítico busca promover buenas prácticas evaluativas en el aula de matemáticas a partir de un diseño metodológico desde un modelo curricular. Teniendo en cuenta los objetivos de la investigación, la estructura metodológica se sustentó en tres fases: caracterización, análisis y diseño. La Tabla 1 presenta las fases y su relación con los objetivos específicos, las actividades, categorías de análisis, fuentes e instrumentos de información.

Fases de la investigación	Objetivos específicos	Actividades	Categoría de análisis	Fuentes de información	Instrumentos de recolección de información
Fase de caracterización.	Caracterizar las prácticas evaluativas que realiza el profesor de matemáticas asociadas al contenido matemático función lineal.	Descripción del tipo de prácticas evaluativas que realiza el profesor de matemáticas cuando evalúa los aprendizajes asociados a la función lineal.	Tipos de prácticas evaluativas según:El momento¿Cuándo evaluar?La finalidad¿Para qué evaluar?La extensión¿Qué dimensiones evaluar?El origen de sus agentes¿Quién evalúa?Su normotipo¿Qué tipo de referente?	Observación de clasesRevisión de instrumentos de evaluación diseñados y gestionados por el profesor.Entrevista a profesores en ejercicio.	Rejilla de observación.Instrumentos de evaluación.Cuestionario de entrevista.
Fase de Análisis	Identificar desde el análisis didáctico buenas prácticas evaluativas para el contenido función lineal.	Definición de elementos desde el modelo curricular “análisis didáctico” que puedan promover buenas prácticas evaluativas en el aula de matemáticas.	Desde el modelo curricular:¿Cuándo evaluar?¿Para qué evaluar?¿Qué dimensiones evaluar?¿Quién evalúa?¿Qué tipo de referente?	Organizadores curriculares del modelo curricular análisis didáctico.	Instrumentos de análisis del modelo curricular.
Fase de diseño	Proponer una estrategia metodológica para promover buenas prácticas de evaluación que aporten al mejoramiento en el aprendizaje de la función lineal.	Diseño de propuesta metodológica para promover buenas prácticas evaluativas en el aula de matemáticas, asociadas al contenido función lineal.	¿Qué significados están asociados al contenido función lineal?¿Qué sistemas de representación?¿Qué fenómenos del contexto social sustenta el contenido?¿Qué objetivos de aprendizaje, capacidades y competencias matemáticas promueve el contenido matemático?¿Qué dificultades y errores se pueden presentar cuando se aprende el contenido matemático?¿Qué tareas matemáticas, materiales y recurso didáctico se pueden diseñar para promover buenas prácticas evaluativas?¿Cómo gestionar tareas matemáticas y como evaluar los aprendizajes logrados en los estudiantes?	Modelo curricular.	Instrumentos de análisis del modelo curricular.

Análisis y tratamiento de datos

En este apartado se presenta cómo se analizaron y se trataron los datos desarrollados en la investigación, por medio de la caracterización de las prácticas evaluativas asociadas a la función lineal que realizaron los profesores de matemáticas. Para ello, se asumieron como fuente de información: la observación de planeaciones y sesiones de clase, el desarrollo de entrevistas semiestructuradas y el análisis de los instrumentos de evaluación que diseñan y gestionan los profesores en el aula.

Las observaciones de las planeación y sesiones de clase

Las observaciones se realizaron teniendo en cuenta los diferentes momentos de la clase y las prácticas evaluativas que realizaron los profesores en cada uno de ellos; de manera específica: el momento uno, “preparación o planeación de la clase”; momento dos, “presentación o introducción del contenido en la clase”; momento tres, “desarrollo de la clase”; y momento cuatro, “cierre de la clase”. La información se registró en la siguiente rejilla, teniendo como referentes los diferentes criterios tipológicos de evaluación sugeridos por Zambrano (2014).

Criterio de observación:__________________	Pregunta que orienta la observación:__________________
	A continuación se presentan las actuaciones de los profesores observadas en las diferentes sesiones de clase, que sustentan lo afirmado
Profesor uno	Profesor dos	Profesor tres
Generalidad:	Generalidad:	Generalidad:
La evaluación al inicio de la clase (evaluación inicial): R:	La evaluación al inicio de la clase (evaluación inicial): R:	La evaluación al inicio de la clase (evaluación inicial): R:
La evaluación durante la clase (evaluación como proceso): R:	La evaluación durante la clase (evaluación como proceso): R:	La evaluación durante la clase (evaluación como proceso): R:
La evaluación al cierre de la clase (evaluación final): R:	La evaluación al cierre de la clase (evaluación final): R:	La evaluación al cierre de la clase (evaluación final): R:

Observación momento dos: “Presentación o introducción del contenido en la clase

Esta observación se realizó con el interés de describir el uso que hacen los profesores de la evaluación en la presentación o introducción del contenido en el aula.

Profesor uno	Profesor dos	Profesor tres
Generalidad:	Generalidad:	Generalidad:
A continuación se registra la actuación del profesor en la que hace uso de la evaluación.	A continuación se registra la actuación del profesor en la que hace uso de la evaluación..	A continuación se registra las actuaciones del profesor en la que hace uso de la evaluación.
A1:	A1:	A1:

Observación momento tres: “Desarrollo de la clase”

Esta observación se realizó con el interés de describir el uso que hacen los profesores de la evaluación durante la enseñanza y el aprendizaje del contenido en el aula.

Profesor uno	Profesor dos	Profesor tres
Generalidad:
	A continuación se presentan las actuaciones de los profesores observadas en las diferentes sesiones de clase, que sustentan lo afirmado
A1: A2:	A1: A2:	A1: A2:

Observación momento cuatro: “Cierre de la clase

Esta observación definió como propósito identificar la forma como el profesor cierra el estudio del contenido en el aula y el papel de la evaluación en ese proceso.

Profesor uno	Profesor dos	Profesor tres
Generalidad:
	A continuación se presentan las actuaciones de los profesores observadas en las diferentes sesiones de clase, que sustentan lo afirmado.
A1:	A1:	A1:

Fuente:Elaboración propia.

Análisis de la información de las observaciones y planeación de las sesiones de clase

Con la información obtenida a partir de observaciones de diferentes sesiones de aula se registra la caracterización de las prácticas evaluativas del profesor de matemáticas en la siguiente rejilla.

Tipos de evaluación	Caracterización de las prácticas evaluativa del profesor de matemática
Según el momento:	Prácticas evaluativas en “la planeación de la clase Prácticas evaluativas en el “desarrollo de la clase Prácticas evaluativas “al cierre de la clase”
Respecto al criterio ¿cuándo evaluar?,	se concluye que:
Según la finalidad	Prácticas evaluativas en “la planeación de la clase Prácticas evaluativas en el “desarrollo de la clase Prácticas evaluativas “al cierre de la clase”
Se concluye respecto al criterio ¿para	qué evaluar?, que
Según el origen de sus agentes	Prácticas evaluativas en “la planeación de la clase Prácticas evaluativas en el “desarrollo de la clase Prácticas evaluativas “al cierre de la clase”
Respecto al criterio ¿quién evalúa? se	concluye que
Según el normotipo	Prácticas evaluativas en “la planeación de la clase Prácticas evaluativas en el “desarrollo de la clase Prácticas evaluativas “al cierre de la clase”
Se concluye que frente a la cuestión ¿qué a evaluación criterial	tipo de referentes usa el profesor al evaluar?,

Fuente:Elaboración propia.

Desarrollo de entrevistas semiestructuradas

Se realizaron entrevistas semiestructuradas a los profesores de matemáticas que permitieran identificar, desde sus discursos, las prácticas evaluativas que realizan asociadas a la función lineal. En la siguiente tabla se registró la información obtenida en las entrevistas realizadas, teniendo como referentes los diferentes tipos de evaluación sugeridos por Zambrano (2014).

Criterio: Según el momento Pregunta orientadora: ¿Cuándo evaluar?
Profesor uno	Profesor dos	Profesor tres
Al inicio:	Al inicio:	Al inicio:
Durante:	Durante:	Durante:
Al finalizar:	Al finalizar:	Al finalizar:
Se puede inferir que
Criterio: Según la finalidad Pregunta orientadora: ¿Para qué evaluar?
Profesor uno	Profesor dos	Profesor tres
Para diagnosticar:	Para diagnosticar:	Para diagnosticar:
Para formar:	Para formar:	Para formar:
Para alcanzar desempeños:	Para alcanzar desempeños:	Para alcanzar desempeños:
Se puede inferir que
Criterio: Según la extensión Pegunta orientadora: ¿Qué dimensiones evaluar?
Profesor uno	Profesor dos	Profesor tres
Global:	Global:	Global:
parcial:	parcial:	parcial:
Se logra identificar que
Criterio: Según el origen de sus agentes Pregunta orientadora: ¿Quién evalúa?
Profesor uno	Profesor dos	Profesor tres
Autoevaluación:	Autoevaluación:	Autoevaluación:
Coevaluación:	Coevaluación:	Coevaluación:
Heteroevaluación:	Heteroevaluación:	Heteroevaluación:
En cuanto
Criterio: Según su normotipo Pregunta orientadora: ¿Qué tipo de referente?
Profesor uno	Profesor dos	Profesor tres
Normativo:	Normativo:	Normativo:
Criterial:	Criterial:	Criterial:
Se puede evidenciar que

Fuente:Elaboración propia.

Análisis del desarrollo de entrevistas semiestructuradas

La información obtenida en las entrevistas permite identificar características asociadas a las prácticas evaluativas de los profesores de matemáticas desde sus discursos. Se propuso la siguiente rejilla para su análisis.

Tipos de evaluación	Caracterización de las prácticas evaluativas del profesor de matemáticas
Según el momento	Al inicio: Durante: Al finalizar:
Según la finalidad	Diagnóstica: Formativa: Sumativa:
Según la extensión	Global: Parcial:
Según el origen de sus agentes	Autoevaluación: Coevaluación: Heteroevaluación:
Según el normotipo	Normativo: Criterial:

Fuente:Elaboración propia.

Los instrumentos de evaluación que diseñan y gestionan los profesores en el aula

En la siguiente tabla se registra la información obtenida de los instrumentos usados por los profesores en sus prácticas evaluativas. Se registró una tabla por cada instrumento analizado.

Criterio: Según la extensión Pregunta orientadora: ¿Qué dimensiones evaluar?
Categorías de análisis (Capacidades matemáticas)	Descripción de prácticas matemáticas
Capacidades desde el saber
C1: Identifica una función lineal en su representación tabular
C2: Identifica una función lineal en su representación gráfica
C3: Identifica una función lineal en su representación algebraica o simbólica
C4: Hace conversiones entre diferentes formas de representación de la función lineal
C5: Hace la gráfica de una función linea
C6: Identifica la variable independiente y la variable dependiente en una función lineal
C7: Identifica el dominio, el codominio y el rango de una función lineal
C8: Explica por qué el codominio y el rango de una función lineal es el mismo
C9: Argumenta la relación entre una función lineal y la proporcionalidad entre dos magnitudes
C10: Halla el valor de la pendiente en una función lineal
C11: Explica el significado de una pendiente negativa en una función lineal
C12: Explica el crecimiento o decrecimiento en una función lineal
C13: Explica la incidencia en la gráfica de una función lineal cuando se suma o resta una cantidad cualquiera
C14: Extrapola valores en la gráfica de una función lineal
Capacidades desde el saber hacer
C1: Identifica y expresa en lenguaje natural situaciones de la vida cotidiana que se puedan modelar con funciones lineales
C2: Grafica funciones utilizando recursos tecnológicos como computador (Geogebra, Derive, etc.) o su celular (aplicaciones como Malmath, Grapher Math Draw, Algeo, etc.)
C3: Modela situaciones de su vida cotidiana mediante una función lineal
C4: Explica el significado de la proporcionalidad en una situación cotidiana
C5: Resuelve problemas relativos a funciones lineales
C6: Crea problemas que se puedan modelar mediante funciones lineales
C7: Predice resultados en situaciones que se comporten como una función lineal
Capacidades desde el saber ser
C1: Aporto ideas al trabajo en equipo
C2: Apoyo a los compañeros que presentan alguna dificultad en algún tema
C3: Me apoyo en los compañeros para aclarar mis dudas
C4: Me esfuerzo por realizar todas las actividades propuestas
C5: Consulto por mi propia cuenta lo que se me dificulta y practico en casa
C6: Me esfuerzo por realizar mis trabajos con calidad

Fuente:Elaboración propia.

Análisis de los instrumentos de evaluación que diseñan y gestionan los profesores en el aula.

Criterio: Según la extensión Pregunta orientadora: ¿Qué dimensiones evaluar?
Categorías de análisis (Capacidades matemáticas)	Descripción de prácticas matemáticas
Capacidades desde el saber
C1: Identifica una función lineal en su representación tabular
C2: Identifica una función lineal en su representación gráfica
C3: Identifica una función lineal en su representación algebraica o simbólica
C4: Hace conversiones entre diferentes formas de representación de la función lineal
C5: Hace la gráfica de una función linea
C6: Identifica la variable independiente y la variable dependiente en una función lineal
C7: Identifica el dominio, el codominio y el rango de una función lineal
C8: Explica por qué el codominio y el rango de una función lineal es el mismo
C9: Argumenta la relación entre una función lineal y la proporcionalidad entre dos magnitudes
C10: Halla el valor de la pendiente en una función lineal
C11: Explica el significado de una pendiente negativa en una función lineal
C12: Explica el crecimiento o decrecimiento en una función lineal
C13: Explica la incidencia en la gráfica de una función lineal cuando se suma o resta una cantidad cualquiera
C14: Extrapola valores en la gráfica de una función lineal
En los instrumentos de evaluación se evidencia
Capacidades desde el saber hacer
C1: Identifica y expresa en lenguaje natural situaciones de la vida cotidiana que se puedan modelar con funciones lineales
C2: Grafica funciones utilizando recursos tecnológicos como computador (Geogebra, Derive, etc.) o su celular (aplicaciones como Malmath, Grapher Math Draw, Algeo, etc.)
C3: Modela situaciones de su vida cotidiana mediante una función lineal
C4: Explica el significado de la proporcionalidad en una situación cotidiana
C5: Resuelve problemas relativos a funciones lineales
C6: Crea problemas que se puedan modelar mediante funciones lineales
C7: Predice resultados en situaciones que se comporten como una función lineal
En relación con las capacidades del saber hacer
Capacidades desde el saber ser
C1: Aporto ideas al trabajo en equipo
C2: Apoyo a los compañeros que presentan alguna dificultad en algún tema
C3: Me apoyo en los compañeros para aclarar mis dudas
C4: Me esfuerzo por realizar todas las actividades propuestas
C5: Consulto por mi propia cuenta lo que se me dificulta y practico en casa
C6: Me esfuerzo por realizar mis trabajos con calidad
Capacidades desde el saber ser

Fuente:Elaboración propia.

Resultados

En este apartado se presentan los resultados logrados con el desarrollo de la investigación articulados a cada uno de los objetivos propuestos.

Resultados asociados a la caracterización de las prácticas evaluativas que realiza el profesor de matemáticas asociadas al contenido matemático de la función lineal

Para caracterizar las prácticas evaluativas que realiza el profesor de matemáticas en el aula, se acogió la tipología de evaluación propuesta por Zambrano (2014), quien realiza una adaptación a las aportaciones de Castillo y Cabrerizo (2010), para plantear una caracterización de la evaluación asociada a las siguientes cuestiones: ¿cuándo evaluar?, referida a los momentos de la evaluación; ¿para qué evaluar?, asociada a la finalidad de la evaluación; ¿qué dimensiones evaluar?, que definen si la evaluación es global o parcial; ¿quién evalúa?, que describe los actores que participan en la evaluación; y ¿qué tipo de referente sustenta la evaluación?, que son aquellas normas o criterios que sustentan la evaluación.

A partir de los elementos aportados desde el referente teórico, para caracterizar las prácticas evaluativas asociadas a la función lineal que realizaron profesores de matemáticas en ejercicio, se asumieron como fuentes de información: la revisión de las planeaciones, la observación a sesiones de clase, el desarrollo de entrevistas semiestructuradas y el análisis de los instrumentos de evaluación que diseñan y gestionan en el aula. A continuación se presentan los resultados obtenidos en cada asunto:

a) Caracterización desde la planeación de la clase de matemáticas:
Se identificó que dentro de las componentes que sustentan el diseño: contenidos, objetivos, metodología y evaluación, esta última es la que menos considera el profesor; los escasos desarrollos que realizan están asociados a la aplicación de pruebas para conocer los desempeños de los estudiantes que permitan generar los reportes institucionales. Desde las cuestiones sugeridas por Zambrano (2014), se identificó que respecto a la pregunta ¿cuándo evaluar?, los profesores consideran evaluar al finalizar la clase, particularmente al cierre de la enseñanza del contenido, con el interés de conocer los niveles de alcance de logros de aprendizaje en los estudiantes; en cuanto a la cuestión ¿para qué evaluar?, los profesores evalúan para conocer desempeños de los estudiantes que permitan promover los reportes de notas. Esta perspectiva deja desprovisto el carácter formativo y permanente de la evaluación, reducida a evaluar, no para conocer la forma en que avanzan los estudiantes en el proceso formativo, sino para informar sobre los desempeños logrados, asignando un carácter instrumental al proceso de evaluar.

En cuanto a la pregunta ¿qué dimensiones se evalúan?, las planeaciones mostraron que los profesores centran el interés en la dimensión cognitiva sobre la dimensión afectiva; ninguna de las planeaciones registró interés por conocer cómo se siente el estudiante cuando aprende el contenido; el interés se fija en qué aprende del contenido, con una mirada fragmentada del mismo. En la misma perspectiva, al indagar sobre ¿quién evalúa?, se identifica únicamente la voz del profesor (heteroevaluación), y es desde su voz que se valoran las diferentes producciones esperadas en los estudiantes. Finalmente, respecto a la cuestión ¿qué tipo de referente sustenta la evaluación?, tal como se ha señalado, el único referente válido es el nivel de alcance de logros en los estudiantes.

b) Caracterización desde la gestión de la clase de matemáticas:
Las prácticas de evaluación de los profesores se caracterizaron por: a) presentación expositiva del contenido; a los estudiantes, con ausencia de tareas que promuevan la comprensión del contenido, b) favorecimiento de la evaluación final como forma de validar si el estudiante resolvió de manera adecuada las actividades sugeridas, y no con intereses formativos que promovieran el aprendizaje de la función lineal a partir de las motivaciones y posibilidades de los estudiantes; c) los profesores se consideran los únicos agentes evaluadores dentro del proceso, ya que todas sus prácticas evaluativas se realizaron desde la heteroevaluación; y d) la evaluación desarrollada por los profesores asume como única norma válida el alcance de logros desde los desempeños de los estudiantes.

Por otra parte, los tres profesores desarrollaron prácticas de aula mediadas por talleres y actividades centradas en la resolución de ejercicios, de manera que los estudiantes pudieran aprender especialmente procesos algoritmizados de la función lineal, con ausencia de actividades que promovieran su comprensión. Desde esta perspectiva, los instrumentos y prácticas evaluativas se centraron en conocer los desempeños de los estudiantes desde la dimensión cognitiva, para generar los registros institucionales de calificaciones. Los profesores desconocen las formas de aprender de sus estudiantes, así como sus formas de negociar significados, validar los conceptos aprendidos, enfrentar y resolver las dificultades.

c) Caracterización desde los discursos de los profesores:
: Fue posible evidenciar que no hay coherencia entre los discursos de los profesores y lo que sucede en realidad en el aula. En las entrevistas los profesores reconocen el papel de la evaluación durante todo el proceso formativo, pero la reducen al cierre de la clase con intereses puramente cognitivos.Desde las cuestiones sugeridas por Zambrano (2014), en los discursos de los profesores se identificó que en la cuestión ¿cuándo evaluar?, consideran importante evaluar al inicio de la clase para identificar los saberes previos de los estudiantes (evaluación inicial), durante el desarrollo de la clase (evaluación como proceso), para conocer la forma en que aprenden los estudiantes y al final de la clase para identificar las capacidades y logros alcanzados (evaluación final). En cuanto al ¿para qué evaluar?, los profesores expresaron la importancia de evaluar para conocer lo que saben los estudiantes antes de abordar el contenido (evaluación diagnóstica), para identificar la forma en que aprenden los estudiantes y acompañar la construcción de conocimiento matemáticos (evaluación formativa) y para determinar los desempeños alcanzados por los estudiantes (evaluación sumativa).

En lo que respecta a ¿qué dimensiones se evalúan?, los profesores consideran relevante evaluar desde la integralidad, es decir, desde el ser, el saber y el saber hacer; sin embargo, resaltan la importancia de la evaluación asociada al saber, sobre las otras dos. En lo referido a ¿quién evalúa?, los profesores consideran importante reconocer la voz de los estudiantes en la evaluación y, por supuesto, la suya. La coevaluación no está presente en sus relatos. En cuanto a ¿qué referente se evalúa?, tanto en la observación de clase como en las entrevistas se reconoce el alcance de los indicadores de logros concretos y prefijados por la institución como sustento para valorar de forma homogénea a los estudiantes y determinar el grado de dominio de la función lineal.

d) Caracterización desde el análisis de los instrumentos de evaluación:
Este se realizó con el interés de identificar lo que evalúan los profesores de la función lineal. El análisis mostró el interés por conocer el dominio de los estudiantes asociados a la representación simbólica de la función lineal, seguida de la representación tabular y gráfica. Hay ausencia de conversiones entre los distintos sistemas de representación. Las actividades para evaluar están desprovistas de ambientes de aprendizaje enriquecidos con información del contexto; son actividades con uso de algoritmos sin la mediación de situaciones problema que impliquen el uso de la función lineal. Desde este referente se identifica el interés de evaluar con fines cognitivos asociados al saber, obviando el saber hacer y el ser. Los instrumentos diseñados permiten al profesor conocer los desempeños de los estudiantes; no se diseñan ni aplican instrumentos para conocer el avance en el aprendizaje desde la voz de los estudiantes; finalmente, solo se evalúa al cierre de la clase.

Resultados asociados a la identificación de buenas prácticas evaluativas desde el análisis didáctico para el aprendizaje de la función lineal

El Análisis Didáctico incorpora conocimientos didácticos de las matemáticas para que los profesores fortalezcan el diseño de currículos locales (preparación de una clase de matemáticas). La siguiente tabla muestra la información que aporta el análisis didáctico para promover buenas prácticas desde la tipología de prácticas sugerida por Zambrano (2014).

Tabla 2

Buenas prácticas evaluativas desde el Análisis Didáctico.

Resultados asociados a la propuesta metodológica para promover buenas prácticas de evaluación que aporten al mejoramiento en el aprendizaje de la función lineal

El diseño de la propuesta metodológica acogió los elementos conceptuales y procedimentales del modelo curricular Análisis Didáctico, lo que favoreció el diseño de tareas matemáticas que permitieran movilizar a los estudiantes a la solución de situaciones problema, en las que activen prácticas matemáticas y, desde esas prácticas, activar capacidades y competencias orientadas al alcance de los objetivos de aprendizaje.

Se diseñaron cinco tareas matemáticas, cada una pensada para favorecer prácticas evaluativas asociadas a los diferentes momentos de enseñanza del contenido función lineal. Todas las tareas incorporaron el diseño de instrumentos que promovieron la autoevaluación, la coevaluación y la heteroevaluación, reconociendo todas las voces de los actores en el proceso de formación, especialmente construir conocimiento matemático a partir de las negociaciones con el otro.

Igualmente, cada una de las tareas incorpora actividades para situar la evaluación como un proceso permanente ligado a las prácticas de enseñanza: al inicio, durante y al cierre de la clase. Las tareas promueven la evaluación formativa, en la que no solo importa el saber, sino el saber hacer y el ser. La siguiente tabla consolida información respecto a las tareas diseñadas:

Momento de la clase	No. tarea	Nombre de la tarea	Tipo de tarea	Propósito de la tarea	Contenidos
Inicio	1	Aprender comprando	Diagnóstica	Explorar los conocimientos previos que tienen los estudiantes respecto a las características de la función lineal y su relación con otros tipos de funciones (afín y constante)	Uso del plano cartesiano, uso de tablas, lenguaje algebraico, operaciones con números reales, diferencia de la relación de función, solución de ecuaciones de primer grado, notación funcional y hallar el valor numérico de expresiones algebraicas
	2	Aprendiendo con los autos	De aprendizaje: presentación del contenido matemático función lineal	Lograr que los estudiantes construyan significados de conceptos básicos de la función lineal: identifique variable dependiente e independiente, dominio, rango, relación de proporcionalidad, pendiente de una función lineal con su respectivo significado y su incidencia en la gráfica.	Variable dependiente e independiente, dominio, rango, relación de proporcionalidad, pendiente de una función lineal con su respectivo significado y su incidencia en la gráfica, así como en su interpretación en términos de la situación dada.
Desarrollo	3	Arroz con leche	De aprendizaje: Sistemas de representación de la función lineal.	Lograr que los estudiantes exploren y comprendan diversas formas de representar la función lineal en situaciones de cambio y variación.	Formas de representación de la función, algebraica, tabular y gráfica.
	4	COVID-19	De aprendizaje: Construcción de modelos usando la función lineal.	Lograr que los estudiantes construyan modelos usando la función lineal para comprender situaciones cotidianas de cambio y variación.	Modelación de funciones lineales, gráficas de funciones lineales por medio de recursos tecnológicos, la proporcionalidad en situaciones cotidianas, creación y predicción de problemas en situaciones que se comporten como una función lineal.
Cierre	5	Transporte y COVID-19	De evaluación: Conocer aprendizajes logrados	Identificar los conocimientos y capacidades matemáticas que los estudiantes adquirieron durante las sesiones anteriores.	Representar gráficamente en el plano cartesiano, identificar los elementos de una función, resolver y proponer problemas de la vida diaria.

Para el diseño de las tareas se definieron las expectativas de aprendizaje como referente para sustentar la enseñanza y evaluación del contenido matemático. La siguiente tabla registra las decisiones tomadas al respecto:

Tabla 4.

Objetivos de aprendizaje, capacidades y competencias matemáticas asociadas a la función lineal.

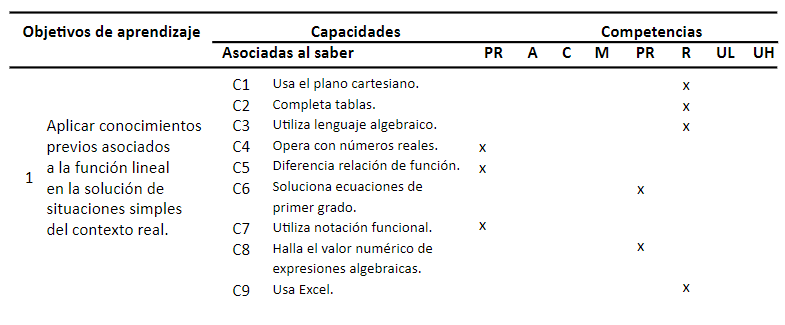
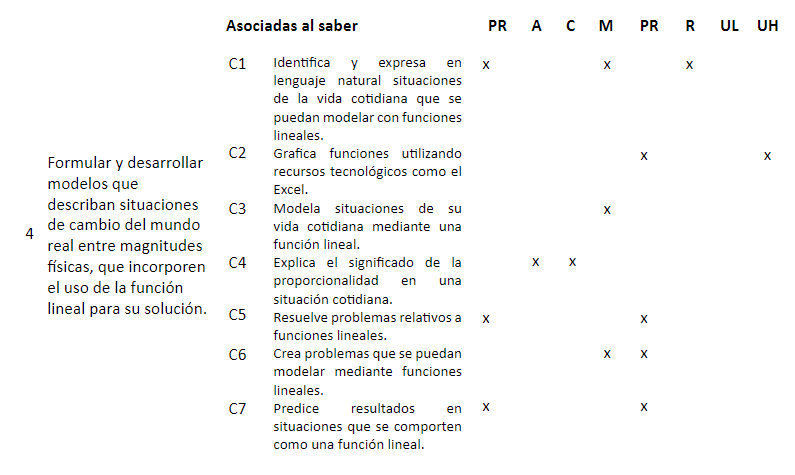
Las competencias corresponden a las definidas en el proyecto PISA: Pensar y razonar (PR), Argumentar (A), Comunicar (C), Modelar (M), Plantear y resolver problemas (PR), Representar (R), Utilizar el lenguaje simbólico, formal y técnico y las operaciones (UL), Usar herramientas y recursos (UH).

Para este documento se presenta el diseño de la tarea matemática cuatro, la cual acoge el objetivo de aprendizaje 4 registrado en la tabla anterior:

Actividades para evaluar al inicio de la clase conocimientos previos.

Descripción de la tarea:

El COVID-19 ha provocado la muerte de personas en todo el mundo; para prevenir su contagio existen los elementos de protección personal, como el tapabocas, guantes y gel antibacterial. Teniendo en cuenta que varios padres de familia del salón han tenido que suspender sus actividades laborales por el confinamiento decretado por el gobierno nacional, uno de los padres consideró vender tapabocas como posibilidad de ingresos para su casa. A continuación, se registran los tipos, costos de los tapabocas y quiénes los compran:

No.	Tipo de tapabocas	Valor por unidad	Usuarios
T1	Tapabocas desechable con filtro	$ 996	Ciudadanos en general
T2	Tapabocas tres capas, lavable	$2000	Personal de servicio doméstico
T3	Tapabocas filtro N95 micropartícula	$ 5000	Operarios y jardineros
T4	Tapabocas N95 antivirus con filt	$7900	Taxistas

El papá de Santiago logró identificar el siguiente comportamiento de la venta de tapabocas durante cada una de las cuatro semanas de los meses de abril y mayo en su negocio, teniendo en cuenta el tipo de clientes que los compran:

• La primera semana inició con un comportamiento en ventas en cada tipo de tapabocas como se registra en la siguiente tabla:

Comportamiento ventas S1, mes de abril según tipo de tapabocas

Tipo de tapabocas	Cantidad de ventas
T1	200
T2	28
T3	50
T4	80

• Cada semana la venta de los tapabocas T1 aumentó en un 15%, lo tipo T2 en u 2%, los tipos T3 en un 5% y los tipos T4 en un 10%.

Con la información registrada realiza las siguientes actividades:

A1:Registra en tablas la información que se deriva de la venta de cada uno de los tipos de tapabocas durante las diferentes semanas de los meses de análisis. Registra las conclusiones que obtienes.
A2:Ubica la información que obtienes de las tablas asociadas al comportamiento de ventas de los diferentes tipos de tapabocas en diferentes planos cartesianos. Registra las conclusiones que obtienes.
A3:Teniendo en cuenta que ya conoces los diferentes significados de la pendiente de la recta, describe para este caso qué sentido le asignas en la venta de tapabocas
A4:Con la información identificada, construye la ecuación lineal que muestra el comportamiento de las ventas en los meses de abril y mayo de cada tipo de tapabocas.

Con las actuaciones de los estudiantes para encontrar las soluciones a las diferentes preguntas planteadas en el contexto de la tarea, se espera que los estudiantes identifiquen cómo, a través de unos datos contextualizados, se pueden formular y desarrollar modelos que describan situaciones involucrando la función lineal.

Actividades para evaluar el desarrollo de la clase

De acuerdo con el problema anterior y con la tabla que se presenta, registra la información correspondiente y responde las diferentes cuestiones.

Tipo de tapabocas	Semanas	Cant. Ventas	Tipo de tapabocas	Semanas	Cant. Ventas	Tipo de tapabocas	Semanas	Cant. Ventas	Tipo de tapabocas	Semanas	Cant. Ventas
T1 Mes Abril	S1 S2 S3 S4		T2 Mes Abril	S1 S2 S3 S4		T3 Mes Abril	S1 S2 S3 S4		T3 Mes Abril	S1 S2 S3 S4
T1 Mes Mayo	S1 S2 S3 S4		T2 Mes Mayo	S1 S2 S3 S4		T3 Mes Mayo	S1 S2 S3 S4		T3 Mes Mayo	S1 S2 S3 S4

A1: ¿Cómo es el comportamiento de las ventas en cada tipo de tapabocas?
A2: ¿Qué diferencias estableces en la cantidad de ventas de cada tipo de tapabocas?
A3: ¿A qué le atribuyes las diferencias?
A4: ¿Qué analizas del tipo de tapabocas y los roles de las personas que los compran?
A5: ¿Qué tipo de tapabocas usas y por qué?
A6: ¿Consideras importante usar el tapabocas y por qué? ¿En dónde debes usarlo?
A7: Ubica la información que obtienes de la tabla en un solo plano cartesiano y registra conclusiones.

Con las actuaciones de los estudiantes para encontrar soluciones a las diferentes preguntas planteadas en el contexto de la tarea, se espera que identifiquen cómo, a través de unos datos contextualizados, se pueden graficar ecuaciones en el plano cartesiano, y formular y desarrollar modelos que describan situaciones involucrando la función lineal.

Actividades para evaluar el cierre de la clase:

Teniendo en cuenta la información suministrada respecto a las dinámicas de ventas de los diferentes tapabocas:

A1: Diseña para el papá de Santiago un análisis financiero que le permita conocer cuál ha sido la cantidad de dinero que ha ganado teniendo en cuenta:

El valor de compra de los tapabocas, así: T1: $650, T2: $1240, T3: $3150, T4: $6480; igualmente, que a cada tapabocas le debe adicionar $100, de gastos operativos (mensajería, gastos de envíos, etc.).

Con la información suministrada, usando la representación que consideres, muestra los gastos generados al papá de Santiago en la compra de los diferentes tapabocas (no olvides considerar los gastos operativos).

A2: Realiza el análisis de cada gasto generado.

A3: Construye la ecuación lineal que muestre las dinámicas de gastos.

A4:Realiza un análisis entre las ventas y los gastos; para ello utiliza gráficas y tablas, que le permitan conocer al papá de Santiago las ganancias por cada tipo de tapabocas y las ganancias totales.

Con las actuaciones de los estudiantes para encontrar las soluciones a las diferentes preguntas planteadas en el contexto de la tarea, se espera que identifiquen cómo formular y desarrollar modelos que describan situaciones involucrando la función lineal

Conclusiones

La investigación permitió reconocer el papel de la evaluación en los procesos de enseñanza del contenido matemático en cada uno de los momentos de la clase; igualmente permitió identificar desde el Análisis Didáctico información útil para favorecer buenas prácticas evaluativas en el aula de matemáticas, prácticas que aprovechan la riqueza del contenido, del contexto y de los estudiantes que aprenden. En la misma perspectiva se contribuyó en mostrar las aportaciones de la evaluación formativa en el favorecimiento de la comprensión del contenido, al conocer no solo lo que aprenden los estudiantes en términos del saber sino, especialmente, cómo se sienten mientras aprenden, desde el ser y saber hacer. Otro elemento a destacar es el alto componente participativo en la evaluación, no solo del profesor, quien tradicionalmente es quien evalúa, sino especialmente de los estudiantes.

Revista Paca 11, Diciembre 2021, ISSN 2027-257X