Artículo de Investigación

Recibido: 11 Agosto de 2018 / Aceptado: 4 Abril de 2020

Diseño y aplicación de secuencias didácticas para fortalecer el aprendizaje de los números enteros y operaciones básicas: suma y multiplicación en estudiantes de séptimo grado de la Institución Educativa Juan Pablo I

Design and application of teaching sequences to trengthen the learning of whole numbers and basic operations: sum and multiplication in seventh grade students of the Juan Pablo I Educational Institution

Desenho e aplicação de sequências didáticas prafortalecer o aprendizado dos números enterros e operações básicas: Suma e multiplicação em estudantes de XXXX série da Instituição Educativa Juan Pablo I

Magister en Educación

Institución Educativa Juan Pablo I

johnnymepe@hotmail.com

Resumen

Los números enteros se encuentran inmersos en la realidad, pues representan situaciones cotidianas como temperaturas bajo cero, deudas, profundidades, pérdidas, años de eventos o etapas históricas, altitudes, entre otros; por lo anterior se detectó la necesidad de realizar una investigación en donde el objetivo general fue: Implementar secuencias didácticas fundamentadas en la teoría del aprendizaje significativo, que fortalezca el aprendizaje de los números enteros y operaciones básicas: suma y multiplicación en los estudiantes de éptimo grado de la Institución Educativa Juan Pablo I. En esta propuesta pedagógica la construcción del conocimiento lo realizaban los estudiantes de manera grupal e individual, aplicando estrategias de lúdica matemática y planteamientos de situaciones problema del contexto cotidiano. La investigación tuvo un enfoque investigativo cualitativo y de tipo Investigación Acción, ya que buscó mejorar las prácticas en el sistema educativo, con acciones de indagación generando una constante reflexión del problema de investigación.

La propuesta pedagógica aludió a una Secuencia didáctica, compuesta por cuatro situaciones didácticas, así mismo fundamentada en la teoría del aprendizaje significativo de David Ausubel. Se desarrollaron actividades secuenciadas en complejidad descritas de la siguiente manera: actividad de apertura, actividades de desarrollo y actividad evaluativa o de cierre. Al finalizar mediante la observación directa, los resultados de la prueba final o evaluativa y las opiniones descritas por los estudiantes se pudo concluir que el uso de estrategias innovadoras como la Secuencia didáctica, lograron motivar a los estudiantes a construir conceptos y sus representaciones, promoviendo de esta manera el aprendizaje significativo.

Palabras clave: Aprendizaje significativo, números enteros, secuencia didáctica, investigación acción.

Summary

The integers are immersed in reality, due to they represent everyday situations such as temperatures below zero, debts, depths, losses, years of events or historical stages, altitudes, among others; Therefore, the need to carry out an investigation was detected where the general objective was: Implement didactic sequences based on the theory of meaningful learning, which strengthens the learning of whole numbers and basic operations: addition and multiplication in seventh-grade students from the Juan Pablo I Educational Institution. In this pedagogical proposal, the construction of knowledge was carried out by the students in a group and individual way, applying mathematical play strategies and problem situations approaches in the daily context. The research had a qualitative and action-type research approach since it sought to improve practices in the educational system, with research actions generating constant reflection on the research problem. The pedagogical proposal alluded to a didactic Sequence, made up of four didactic situations, also based on David Ausubel’s theory of significant learning. Sequential activities in complexity were carried out, described as follows: opening activity, development activities, and evaluative or closing activity. When concluding through direct observation, the results of the final or evaluative test and the opinions described by the students, it was possible to conclude that the use of innovative strategies such as the didactic sequence, managed to motivate the students to build concepts and their representations, promoting this way meaningful learning.

Keywords: Meaningful learning, integers, didactic sequence, action research.

Resumo

Os números inteiros encontram-se imersos na realidade, pois representam situações cotidianas como temperaturas embaixo de zero, dívidas, profundidades, perdas, anos de eventos ou fases históricas, altitudes, entre outros; Por isso detectou-se a necessidade de realizar uma pesquisa onde o objetivo geral foi implementar sequências didáticas fundamentadas na teoria do aprendizado dos números inteiros e operações essenciais: suma e multiplicação nos estudantes de XX série da Instituição Educativa Juan Pablo I. Nesta proposta pedagógica a construção do conhecimentos era realizada por estudantes de forma grupal e individual, usando estratégias de lúdica matemática e exposições de situações problema do contexto cotidiano. A pesquisa teve um foco de pesquisa qualitativa e de pesquisa-ação, pois procurou melhorar as práticas no sistema educativo, com ações de indagação gerando uma reflexão constate do problema de pesquisa.

Palavras-chave: Aprendizagem significativa, números inteiros, sequência didática, pesquisa-ação.

Introducción

El aprendizaje significativo es una de las teorías más utilizadas en el contexto educativo, y en la presente investigación es el enfoque y objetivo que se desea alcanzar en los estudiantes del grado séptimo de la Institución Educativa Juan Pablo I, esta teoría fue creada por David Ausubel quien en 1976 describió según Rodríguez (2004):

El aprendizaje significativo es el proceso según el cual se relaciona un nuevo conocimiento o información con la estructura cognitiva del que aprende de forma no arbitraria y sustantiva o no literal. Esa interacción con la estructura cognitiva no se produce considerándola como un todo, sino con aspectos relevantes presentes en la misma, que reciben el nombre de subsumidores o ideas de anclaje. (p.2)

Además, Ausubel también da importancia a la predisposición del estudiante frente al proceso de construcción de significados o nuevo conocimiento, por ello la presente investigación buscó promover la motivación al estudiante y que de esta manera se pudiera facilitar el aprendizaje significativo del que alude Ausubel en su teoría, el cual fundamenta también esta investigación.

Se planteó una propuesta pedagógica representada como una Secuencia didáctica, la cual se define según González, Kaplan, Osua & Reyes (2010) como una sucesión planificada y estructurada de actividades, que se desarrollarán en un período de tiempo determinado. Esta tiene como objetivo implementar secuencias didácticas fundamentadas en la teoría del aprendizaje significativo, que fortalezca el aprendizaje de los números enteros y operaciones básicas: suma y multiplicación. Para el desarrollo de la misma se tuvo en cuenta la recomendación de Ausubel en 1991 acerca del trabajo de pequeños grupos en el contexto escolar, la cual junto a las situaciones problema Guzmán en 1993 citado en Mazarío, Mazarío y Horta (2002), indica que “La tarea de solución de problemas será más efectiva cuando se resuelva en pequeños grupos de trabajo, pues proporciona posibilidad de enriquecimiento, el grupo proporciona apoyo y estímulo, permite contrastar los progresos” (p.42). También se utiliza la lúdica matemática y estrategias lingüísticas como sopas de letras, crucigramas, entre otros.

La propuesta pedagógica se plantea para abordar una solución a la problemática detectada con relación a las dificultades en la comprensión de las nociones semánticas, sintácticas y estructurales de los números enteros, y sus representaciones simbólicas, gráficas y verbales; repercutiendo en el desempeño académico y el no cumplimiento de los logros académicos.

Conceptos de número entero

El conjunto de los números enteros está definido como una relación de equivalencia del conjunto N × N (N = números naturales) tal que (a, b) R (c, d) ↔ a + d = b + c donde cada pareja de elementos (a, b) le corresponda un numero llamado entero Z = (a − b), ejemplo: la pareja (2,5) le corresponde el número entero Z = (2 − 5) = −3.

Según Rodríguez (2013) el conjunto Z es un conjunto de números dotado de una operación interna (+) en el que sus elementos tienen un simétrico respecto de (+), y este contiene los naturales N, Z⁻ (números negativos) y el cero, manteniendo un isomorfismo entre sus componentes, que conserve la adición, multiplicación y el orden, pudiéndose identificar los elementos de ambos conjuntos.

Conceptos de número negativo

Alber Girard (citado en Maz, 2005) considera a “los negativos como valores algebraicos, cuyo significado no tiene por qué estar vinculado a una magnitud física; estos números se usan como distintos de las cantidades aritméticas” (p.8).

El número negativo es aquel número natural precedido de un signo -, y su valor es menor que cero, Según Velasco, Rojas y Gallardo (s.f) para indicar la posición o desplazamiento de un cuerpo, hemos necesitado además de los números naturales, de otros números que se escriben en la recta numérica a la izquierda del cero, en su relación de orden es mayor aquel que está más cercano al número cero, contrario a los números naturales. Se utilizan para representar situaciones como temperaturas bajo 0, altitudes con relación al nivel del mar, pérdidas o déficits, para referirnos históricamente a los años antes de Cristo e indicar superficies subterráneas.

Según Glaeser (Citando en Cid, s.f.) los obstáculos que han existido durante la evolución histórica de la noción de número negativo han sido:

- Falta de aptitud para manipular cantidades negativas aisladas.

- Dificultad para dar sentido a las cantidades negativas aisladas.

- Dificultad para unificar la recta real.

- La ambigüedad de los dos ceros: un cero que significa la ausencia de cantidad, a un cero de origen elegido.

- El estancamiento en el estadio de las operaciones correctas.

- Deseo de un modelo unificador.

Concepto de número cero

Según Mónaco (2009) el cero “pertenece al conjunto de los números enteros que sigue al -1 y precede al 1” (p. 14), así mismo el cero se considera como elemento de los números naturales, porque representa al conjunto vacío que no tiene elementos; también representa la suma entre un número y su opuesto.

El número cero representa el origen o inicio de algo, se le toma como punto de referencia, también significa la ausencia total de algo por lo tanto el número cero describe el inicio o fin de un proceso.

Según Glaeser citado en (Cid. s.f) la ambigüedad de los dos ceros hace alusión a:

Las dificultades que hubo entre los matemáticos (Stevin, McLaurin, D’Alembert, Carnot, Cauchy y, quizá, Euler y Laplace) para pasar de un cero absoluto, un cero que significaba la ausencia de cantidad de magnitud, a un cero origen elegido arbitrariamente. Uno de los razonamientos más extendidos entre los matemáticos que se oponían a la consideración de las cantidades negativas como cantidades reales y no como meros artificios del cálculo, era que no se podía admitir la existencia de cantidades que fueran menos que nada. (p. 4)

Con relación a las operaciones básicas de suma y multiplicación, el cero en la suma se considera el elemento neutro, lo que significa que cualquier cantidad sumada con el cero da como resultado la misma cantidad; y en la multiplicación es considerado como el elemento anulativo, pues cualquier cantidad multiplicada por cero da como producto, cero.

Relación de orden

Los números enteros al ordenarlos presentan tres situaciones:

- Si son positivos ambos enteros, será mayor el de mayor cantidad, en una recta numérica se puede observar como el que esté más alejado del cero o más hacia la derecha.

- Si ambos enteros son negativos será mayor el de menor cantidad. En la recta se puede ver como el que está más cercano al número cero.

- Si un entero es positivo y el otro es negativo será mayor siempre el positivo.

A continuación, se definirán las propiedades que se cumplen en el orden de los números enteros descritos por Olivan (s.f):

Definición: Sean a, b ∈ Z. Se dice que a ≥ b ⇔ a − b ∈ N.

Proposición: El orden de los números enteros tiene las siguientes propiedades:

a) Reflexiva: ∀a ∈ Z : a ≥ a

b) Antisimétrica: Si a ≥ b y b ≥ a ⇒ a = b

c) Transitiva: Si a ≥ b y b ≥ c ⇒ a ≥ c

d) Conexa: ∀a, b ∈ Z ⇒ a ≥ b ó b ≥ a, es decir, todos los elementos de Z son comparables.

Suma de números enteros

La suma de números enteros está definida como la relación: Z × Z → Z siendo (a, b),(c, d) ∈ N × N se tiene [(a, b)] + [(c, d)] = [(a + c.b + d)].

La adición de números enteros puede presentarse en tres casos según Rodríguez (2013, p.164).

1°) Suma de dos enteros positivos.- [(a, 0)] + [(b, 0)] = [(a + b, 0 + +0)] = [(a + b, 0)] → resultado positivo.

2°) Suma de dos enteros negativos.- [(0, a)] + [(0, b)] = [(0 + 0, a + +b)] = [(0, a + b)] → resultado negativo.

3°) Suma de un entero positivo y otro negativo, o viceversa. [(a, 0)] + [(0, b)] = [(a + 0, 0 + +b)] = [(a, b)], de donde deducimos que:

- El resultado es positivo si a > b, ya que ntonces (a, b) ≈ (a–b, b–b) =⇒ (a, b) ≈ (a–b, 0), lo cual simboliza un entero positivo, pues a–b ∈ N∗.

- El resultado es negativo si a < b, ya que ahora (a, b) ≈ (a–a, b–a) −→−→ (a, b) ≈ (0, b–a), lo cual simboliza un entero negativo, pues b–a ∈ N∗.

-El resultado es nulo si a = b, dado que (a, b) ≈ (a, a) ≈ (0, 0).

Al sumar dos números enteros a, b ∈ Z se debe tener en cuenta lo siguiente:

- Si es a > 0 y b > 0 entonces a + b > 0 significa que al sumar dos números positivos se tiene como resultado otro número positivo entero. Ejemplo:

- Si a = 3 y b = 5 entonces 3 + 5 = 8 > 0

- Si a < 0 y b < 0 entonces a + b < 0 expresa que al sumar dos números negativos se tiene como resultado otro número entero negativo, ejemplo:

- Si a = −2 y b = −5 entonces −2 + (−5) = −2 − 5 = −7 < 0.

- Si a > 0 y b < 0 la suma de a + b es igual a la resta del mayor valor absoluto con el menor valor absoluto y su resultado lleva el signo del número que tenga mayor valor absoluto, ejemplo:

- Si a = 8 y b = −12 entonces 8 + (−12) = 8 − 12 = −4

Multiplicación de números enteros

La multiplicación de números enteros está definida como la relación: Z × Z → Z. Siendo (a, b),(c, d) ∈ N x N se tiene [(a, b)] · [(c, d)] = [(a · c + b · d, a · d + b · c)] = [(ac + +bd, ad + bc)].

Según Rodríguez (2013, p. 174) en la multiplicación de números enteros pueden presentarse tres casos, considerando a, b ∈ N∗:

1°) Producto de dos enteros positivos. [(a, 0)]·[(b, 0)] = [(a·b, 0)] −→ resultado positivo.

2°) Producto de dos enteros negativos. [(0, a)]·[(0, b)] = [(a·.b, 0)] −→ resultado positivo; es decir que al multiplicar dos cantidades negativas se tiene como producto una cantidad positiva. Ejemplo: (−3).(−5) = 15

3°) Producto de un entero positivo y otro negativo, o viceversa.

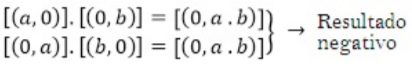
Al multiplicar dos números enteros a,b ∈ Z se debe tener en cuenta lo siguiente:

Si es a > 0 y b > 0 entonces a · b > 0 significa que al multiplicar dos números positivos se tiene como producto otro número positivo entero. Ejemplo:

Si a = 7 y b = 9 entonces 7 · 9 = 63 > 0.

Si a < 0 y b < 0 entonces a · b > 0 expresa que al multiplicar dos números negativos se tiene como producto un n´umero entero positivo. Ejemplo:

Si a = −5 y b = −6 entonces (−5) · (−6) = 30 > 0.

Si a > 0 y b < 0 entonces a · b < 0 al multiplicar un entero positivo con un negativo da como producto un número entero negativo. Ejemplo:

Si a = 4 y b = −15 entonces 4 · (−15) = −60 < 0.

Secuencia didáctica

El docente juega un papel importante en el aprendizaje de los estudiantes, siendo éste un orientador y guía haciendo utilidad de procesos de intervención reflexivos, intencionales, colaborativos, que promuevan el descubrimiento de nuevos conocimientos que refuercen los adquiridos previamente; por lo tanto hace uso de la secuencia didáctica siendo esta según González, Kaplan, Osua & Reyes (2010)una sucesión planificada y estructurada de actividades, que se desarrollarán en un periodo de tiempo determinado, así mismo representa una herramienta de suma importancia para el aprendizaje autorregulado, puesto que las actividades son secuencialmente preparadas por un facilitador, en este caso el docente.

Según Pérez y Roa (2010) la secuencia didáctica es “una estructura de acciones e interacciones relacionadas entre sí, intencionales, que se organizan para alcanzar algún aprendizaje”, además se pueden diseñar con la finalidad de construir saberes, debido a que son unidades de trabajo que se focalizan en un trabajo específico, por lo tanto, también hace uso de la vinculación de saberes y saberes hacer n particular. Es necesario que dentro de la secuencia didáctica se evidencie claramente la construcción sucesiva de complejidad entre las actividades. Continuando con la importancia de la secuencia didáctica Díaz (s.f) indica que estas permiten desarrollar un aprendizaje significativo, es por ello que para su creación o elaboración el docente debe tener conocimientos sobre la asignatura, así como una clara comprensón del programa de estudio y tener una visón pedaógica establecida.

Por otra parte, Díaz (S.f) plantea una estructura de las secuencias didácticas donde deja observar dos elementos los cuales son realizados de manera paralela, y estos son la secuencia de las actividades para el aprendizaje y la evaluación para el aprendizaje; contemplando estos dos principios en sus tres dimensiones: diagnóstica, formativa y sumativa.

Desde el principio de la secuencia es necesario tener claridad de las actividades de evaluación para el aprendizaje, incluso es importante lograr una visión integral de las evidencias de aprendizaje, superar la perspectiva de sólo aplicar exámenes, sin necesidad de eliminarlos completamente, pero sobre todo reconociendo que los principios trabajo por problemas y perspectiva centrada en el aprendizaje significan lograr una articulación entre contenidos (por más abstractos que parezcan) y algunos elementos de la realidad que viven los alumnos. De esta manera, construcción de una secuencia de aprendizaje y evaluación son elementos que van de la mano y se influyen mutuamente (p.4).

Para el desarrollo del proyecto investigativo se hará utilidad de la herramienta pedagógica de secuencia didáctica con la finalidad de lograr el aprendizaje significativo de los estudiantes con relación a los números enteros y las operaciones básicas de suma y multiplicación, debido a que es una herramienta flexible que permite la creación y afianzamiento de nuevas conceptualizaciones, las cuales a su vez apoyen los conocimientos previos y que amplíen una nueva comprensión de la matemática.

Teoría de Aprendizaje significativo

Ausubel (citado en Rodríguez, 2010) plantea en su teoría del aprendizaje significativo un marco teórico donde la finalidad es poder dar cuenta de aquellos mecanismos por los que se adquiere y se logra la retención de significados que son manejados en la etapa escolar; haciendo énfasis en lo que ocurre en el aula cuando un estudiante aprende, así como en la naturaleza del aprendizaje, las condiciones y los resultados consecuentes a la evaluación de estos. En la actualidad la teoría del aprendizaje significativo ha tenido gran acogida en el lenguaje de los docentes, puesto que su fin es el de ocuparse de facilitar los aprendizajes en el aula, si bien es cierto no es tan vivencial en sus prácticas educativas, posiblemente por el desconocimiento acerca de las herramientas que brinda. Ausubel (citado en Martin, 2005) ofrece una nueva perspectiva en la que la estructura cognitiva de los estudiantes es ahora tenida en cuenta para el desarrollo de herramientas metacognitivas permitiendo en la actualidad a los docentes ejecutar una labor de enseñanza no con “mentes en blanco” ni comenzando desde “cero”, sino al contrario investigando que es lo que el estudiante “ya sabe” y a partir de allí enseñar consecuentemente (p.2).

Además, Pozo (1989) considera esta teoría como una teoría cognitiva de reestructuración, en donde expresa “se ocupa específicamente de los procesos de aprendizaje/enseñanza de los conceptos científicos a partir de los conceptos previamente formados por el niño en su vida otidiana [. . . ]. Ausubel desarrolla una teoría sobre la interiorización o asimilación, a través de la instrucción” (p. 209), por lo que da realce a la concepción de que el propio individuo es el que genera y construye su aprendizaje. Por otro lado con relación a la perspectiva ausubeliana, para que se produzca un aprendizaje significativo han de darse dos condiciones fundamentales según Palermo (2004):

- Actitud potencialmente significativa de aprendizaje por parte del aprendiz, o sea, predisposición para aprender de manera significativa.

- Presentación de un material potencialmente significativo. Esto requiere, por una parte, que el material tenga significado lógico, es decir, que sea potencialmente relacionable con la estructura cognitiva del que aprende de manera no arbitraria y sustantiva; y, por otra parte, que existan ideas de anclaje o subsumidores adecuados en el sujeto que permitan la interacción con el material nuevo que se presenta. (p.2)

Es importante resaltar que una de las condiciones que nombra Ausubel (citado en Moreira, 1997) acerca de su teoría es que los nuevos aprendizajes se relacionan de una manera no arbitraria y sustantiva. Cuando el autor habla acerca de la no-arbitrariedad hace referencia a que el nuevo material no se va a relacionar con toda la estructura cognitiva, sino con los aspectos relevantes los cuales también son denominados por el autor como los “subsumidores”, siendo por lo tanto el conocimiento anterior una matriz ideacional y los nuevos conocimientos puntos de anclaje que se relacionen con los anteriores. Por otra parte, Ausubel considera la sustantividad como una característica que define que lo que se llega a incorporar es la sustancia del nuevo conocimiento, es por ello por lo que si se utilizan diferentes signos para expresar un concepto o idea pueda de igual manera el estudiante comprenderla por que anteriormente la ha aprendido (p.2).

Metodología

La investigación se encuentra enmarcada en un enfoque investigativo de tipo cualitativo, el cual hace referencia, según Hernández Sampieri (2014), a un proceso inductivo contextualizado en un ambiente natural, en este tipo de enfoque las variables no se manipulan experimentalmente; en esta no se reduce a números las conclusiones obtenidas de los datos, buscando ser más amplia que los contrastes delimitados del enfoque cuantitativo. Este tipo de enfoque abarca una mayor cantidad de ideas e interpretaciones, puesto que busca comprender un fenómeno social, más allá de la sola medición de variables.

Seguidamente se afirma que el proyecto se encuentra enmarcado en el tipo de investigación acción, termino proveniente de Kurt Lewis, en donde hace referencia a múltiples estrategias que se desarrollan con la intencionalidad de mejorar el sistema educativo y social. Este tipo de investigación liga el enfoque experimental de la ciencia social con la acción social, según Murillo (2011). Además, se trata de una constante reflexión sobre las acciones humanas con relación a las situaciones vividas en el aula de clase, pudiendo de esta manera comprender de manera amplia los problemas que se presentan en dicho contexto.

Por otro lado, Kemmis (citado en Morris, 2011) describe a la investigación acción como no solamente una ciencia práctica y moral, sino además como una ciencia crítica, puesto que indica que esta es:

[. . . ] una forma de indagación auto reflexiva realizado por quienes participan (profesorado, alumnado, o dirección, por ejemplo) en las situaciones sociales (incluyendo las educativas) para mejorar la racionalidad y la justicia de: a) sus propias prácticas sociales o educativas; b) su comprensión sobre las mismos; y c) las situaciones e instituciones en que estas prácticas se realizan (aulas o escuelas, por ejemplo).

Debido a lo que este tipo de investigación tiene como objetivo en las ciencias sociales, es qué ha tenido gran auge dentro de la comunidad educativa, además es por ello por lo que se considera de vital importancia enmarcar este proyecto investigativo en ella. Por otra parte, la investigación acción posee diversas fases, las cuales serán tenidas en cuenta como desarrollo metodológico del presente proyecto investigativo.

Según Tamayo y Tamayo (1997), Cuando seleccionamos algunos elementos con la intención de averiguar algo sobre una población determinada, nos referimos a este grupo de elementos como muestra. Por supuesto, esperamos que lo que averiguamos en la muestra sea cierto para la población en su conjunto. La exactitud de la información recolectada depende en gran manera de la forma en que fue seleccionada la muestra.

El estudio referente al diseño y aplicación de secuencias didácticas para fortalecer el aprendizaje de los números enteros y operaciones básicas: suma y multiplicación, requiere de la selección de la muestra con respecto a la población, la cual constituye la fuente de la investigación; por ello el número de participantes o muestra son treinta y seis estudiantes del grado séptimo 7-01 de la jornada de la tarde sede principal de la Institución Educativa Juan Pablo I.

Para la recolección de información se utilizarán instrumentos tales como: Diario de campo o pedagógico, prueba diagnóstica, videos, prueba final, entrevistas, otras.

Diario pedagógico: El diario pedagógico es un instrumento que permite describir los acontecimientos registrados entre el docente y los estudiantes durante los diferentes momentos de clases en el proceso de aprendizaje, elemento que permite analizar y llevar a un plan de mejor la práctica pedagógica del docente, ya que permite plasmar literalmente las situaciones expresadas por los estudiantes y analizar las mismas fundamentadas en la teoría.

Observación directa: Según Benguria, Alarcón, Valdés, Pastellides y Colmenarejo (2010), la observación directa es aquella en la ue el observador se pone en contacto directa y personalmente con el hecho o fenómeno a observar.

Prueba diagnóstica: La prueba diagnóstica permite identificar las debilidades y fortalezas que poseen los estudiantes referente a la comprensión del concepto de números enteros, la relación de orden de los enteros, identificación de los signos, conceptualización del cero y negatividad, permitiendo conocer qué presaberes poseen los estudiantes y como se encuentra el nivel de competencias matemáticas que facilitan el aprendizaje de los números enteros en los estudiantes de séptimo grado, 7-01, de la Institución Educativa Juan Pablo I.

Prueba final: La prueba final permite valorar los aprendizajes alcanzados en el aprendizaje de los números enteros por los estudiantes de grado séptimo, 7-01, de la Institución Educativa Juan Pablo I cada vez que se hayan aplicado las secuencias didácticas diseñadas en la implementación de esta estrategia pedagógica. Dicha prueba será igual a la prueba final.

Resultados

El proyecto de investigación plantea una propuesta pedagógica con el objetivo de implementar secuencias didácticas fundamentadas en la teoría del aprendizaje significativo, que fortalezca el aprendizaje de los números enteros y operaciones básicas: suma y multiplicación en los estudiantes de séptimo grado de la Institución Educativa Juan Pablo I. Esto con la finalidad de lograr un aprendizaje significativo en los estudiantes haciendo uso fundamental de los presaberes que poseen.

Según Pozo en Rodríguez (2004) la teoriza de Ausubel acerca del aprendizaje significativo es “una teoría constructivista, ya que es el propio individuo- organismo el que genera y construye su aprendizaje” (p. 2).

El proyecto se desarrolló en 32 sesiones, cada una con duración de 60 minutos, las cuales se concretaron en un total de 8 semanas; se aplicó una secuencia didáctica con cuatro situaciones didácticas denominadas de la siguiente manera:

- Concepto de numero entero.

- Orden de los números enteros.

- Suma de números enteros.

- Multiplicación de números enteros.

A su vez cada una de las situaciones didácticas se componían de actividades de apertura, desarrollo y evaluativas. Se abordan conceptualizaciones referentes a la temática tales como, número negativo, número cero, número natural, elemento simétrico o inverso aditivo, valor absoluto, recta numérica, concepto y propiedades de la suma y multiplicación; lo anterior con la finalidad de que el estudiante logre aportar soluciones con base en los números enteros y sus operaciones básicas a situaciones problemas cotidianos.

Debido a la naturaleza del proyecto de tipo investigación acción los resultados fueron obtenidos mediante la aplicación de los instrumentos de investigación como el diario de campo, prueba diagnóstica, prueba final y la observación directa, se especifica que, según Huamán (2005), la observación directa es un “proceso activo y voluntario gracias a la atención prestada y teniendo siempre presente el objeto que se pretende conseguir” (pp. 13-16). Así mismo, este autor especifica a la observación directa como la puesta en contacto personal del investigador con el hecho o fenómeno que trata de investigar.

Para este proyecto se utilizó la observación de campo el cual, según Huamán (2005), es el “recurso principal de la observación descriptiva, se realiza en los lugares donde ocurren los hechos o fenómenos investigados” (pp.13-16), aclarando que las investigaciones de tipo social y educativas son las que más recurren a este tipo de observación. Así mismo, se plantearon una serie de categorías y subcategorías, con las cuales se organizó la información recolectada y se pudo observar con mayor claridad al objeto de estudio, pudiendo medir el cumplimiento de los indicadores establecidos. Las categorías y subcategorías fueron: conjunto de números enteros (CE 1), siendo subcategorías: conceptualización de Z (CE 1.1) e interpretación y representación de Z (CE 1.2). La segunda categoría se denominó interrelación cognitiva (IC 1), teniendo como subcategorías el aprendizaje significativo (IC 1.1) y las situaciones problema (IC 1.2). La tercera categoría fue el desempeño del estudiante (DE 1), en donde se incluyeron las subcategorías de participación e interacción grupal (DE 1.1) y evaluación (DE 1.2).

Con relación a los aprendizajes significativos obtenidos por los estudiantes durante el proceso de desarrollo de la secuencia didáctica, se evidenció según la categoría DE 1 en la subcategoría DE 1.1 mayor disposición a ejecutar las actividades propuestas a causa de la proporción del material didáctico e innovador tales como: dados, juegos de cartas, rompecabezas, laminas para dibujar figuras geométricas, actividades de sopa de letras y crucigramas, fichas adhesivas; permitiéndoles una experiencia nueva a desarrollar. Respecto a la subcategoría DE 1.2 se infiere que el conocimiento que fue adquirido no fue directamente trasmitido, sino vivenciado mediante las actividades y la participación de cada uno, observándose actitudes de trabajo colaborativo mediante la formación de equipos de trabajo y participación en debates, así como la socialización de opiniones. Con relación a la categoría CE 1 específicamente la subcategoría CE 1.1, los estudiantes desarrollaron elpensamiento numérico y variacional, la aplicación de conceptos matemáticos como el concepto de número entero y así mismo la aplicación de las operaciones básicas en el contexto sociocultural y escolar. También se logró en la subcategoría CE 1.2 que relacionaran cantidades mayores, menores o iguales entre sí como diferenciar la cantidad de dinero que poseen para comprar en la tienda escolar, la diferencia de edades entre ellos; utilizar el cero en situaciones que representan el inicio o el fin de un proceso teniendo ahora mayor claridad de las representaciones de sucesos. Por ejemplo: como el nacimiento de Cristo como un punto de inicio para indicar fechas, el inicio y el final de actividades escolares programadas como actos culturales y deportivos, se observó que el lenguaje utilizado por los estudiantes con respecto a situaciones tales como deudas adquiridas por préstamo de dinero y pérdidas al realizar negocios entre ellos, las expresaban como un número negativo. De esta manera obtuvieron una visión ampliada de las matemáticas en el mundo real.

Además en la subcategoría CE 1.2 lograron diferenciar una cantidad de otra a través de su valor absoluto, sumar cantidades positivas y negativas que originan en algunos casos diferencias, observándose que algunos estudiantes sumaban sus deudas y diferenciaban con el dinero que poseían para lograr saber cuánto dinero les quedaba; así como escribir de diferentes formas una suma y una multiplicación a través de las propiedades, lograron comprender que existen sistemas de referencia como el nivel del mar para determinar profundidades y alturas. Además, identificaron que las temperaturas bajo cero se pueden representar con números negativos y tuvieron en cuenta el sentido de las cantidades al operar, comprendieron la ley de los signos.

Según la categoría IC 1 con relación a la subcategoría IC 1.1, el docente logra la planeación de estrategias pedagógicas en donde presentó los nuevos conocimientos teniendo en cuenta la estructura cognitiva e ideacional que ya poseían los estudiantes, favoreciendo de esta manera el aprendizaje significativo de nuevos conocimientos, lo cual se evidencia en los debates y opiniones emitidas por los estudiantes frente a la resolución de problemas con números enteros. Así mismo la subcategoría IC 1.2 arrojó resultados favorables, ya que las situaciones problemas de la cotidianidad y del contexto escolar, permitieron a los estudiantes aportar soluciones manejando la conceptualización de números enteros, y sus operaciones de suma y multiplicación. Continuando con el análisis se logro implementar una propuesta pedagógica fundamentada en secuencia didáctica consiguiendo de esta manera favorecer el aprendizaje de sus estudiantes, así como lograr la participación y motivación de estos frente a las actividades planteadas, resolvió dudas e inquietudes de los estudiantes. Según Ausubel (1983) “el docente es un facilitador del aprendizaje, además es un conocedor de la estructura cognitiva del alumno, no únicamente se trata de saber la cantidad de información que posee, sino cuales son los conceptos y proposiciones que maneja, así como su grado de estabilidad” (p. 2).

Finalmente, en algunas ocasiones una minoría de los estudiantes manifestaron cosas tales como “tengo dolor de cabeza”, “permiso para ir al baño” y otros posicionaron su cabeza sobre el pupitre manifestando sueño como un medio de evasión a la ejecución de las actividades.

Conclusiones

Se concluye con relación a la pregunta de investigación, que mediante la aplicación de la propuesta pedagógica de una secuencia didáctica se logró fortalecer el aprendizaje de los números enteros y las operaciones básicas de suma y multiplicación en los estudiantes del grado 7- 01 de la Institución Educativa Juan Pablo I, para ello fue importante la aplicación de actividades secuenciadas en complejidad, teniendo en cuenta la estructura cognitiva de presaberes de los estudiantes y el uso de material didáctico, además se observó una participación activa y grupal, con responsabilidad de construcción del conocimiento.

Mediante una prueba diagnóstica se logró detectar que los estudiantes inicialmente no tenían apropiación de conceptos como número entero, número negativo y el número cero, además desconocían que se podía operar mediante una suma y/o multiplicación un número positivo con uno negativo, o dos números negativos. También desconocían la relación de orden entre números negativos, confundían las propiedades de la suma y la multiplicación, se les dificultaba definir e identificar un sistema de referencia y representar situaciones problema de la cotidianidad con números enteros u operaciones de enteros.

Además, se tuvo en cuenta la identificación de los presaberes que tenían los estudiantes con respecto a la temática a trabajar, seguido a esto se diseñó una secuencia didáctica con cuatro situaciones didácticas teniendo en cuenta que cada una aumentaría en complejidad con relación a la conceptualización, utilización de signos y los ejercicios a trabajar.

También fue de gran utilidad la realización de debates, mesas redondas, preguntas verbalizadas por el docente y situaciones problema planteadas de acuerdo con la realidad de los estudiantes; ya que se favoreció que los conceptos fueran trasladados a contextos reales y puestos en práctica. Finalmente se tuvieron en cuenta las representaciones graficas o ilustraciones que permitieron la comprensión con mayor facilidad de la temática. Posteriormente, se concluye que la mayoría de los estudiantes del grado 7- 01 lograron comprender la temática de números enteros, incluyendo ahora los números negativos en su representación mental y hacer uso de ellos para representar situaciones. También se observó una nueva perspectiva del aprendizaje de la matemática debido a la estrategia de la lúdica matemática y la construcción del conocimiento, viéndose reflejado en el rendimiento académico del área de matemáticas. Se concluye a partir de lo descrito anteriormente, que la secuencia didáctica diseñada y puesta en práctica fue de gran impacto para los estudiantes, permitió incentivar la responsabilidad por la construcción del conocimiento, favoreció la exploración del material proporcionado para abordar soluciones de las situaciones problema. Además, el implementar una propuesta pedagógica innovadora trajo consigo un componente importante tal como la motivación del estudiante, y con ello la participación activa y propositiva individual y grupal.

Referencias

Benguría, S., Alarcón, B., Valdés, M., Pastellides, P., & Gómez, L. (2010). Métodos de investigación en Educación Especial. Recuperado de http://uam.es/personal pdi/stmaria/jmurillo/InvestigacionEE/Presentaciones/Curso_10/Grup_discusion_2-trabajo.pdf

Blanco, D. (2014). Implementación de Scratch para potenciar el aprendizaje significativo a través lógica de programación en los estudiantes de Nivel Básica Secundaria. Recuperado de https://www.researchgate.net/publication/270880545 Implementacion_de_Scratch_para_potenciar_el_aprendizaje_significativo>_a_traves_logica_de_programacion_en_los_
estudiantes_de_Nivel_Basica_Secundaria

Blasco, J., & Pérez, J. (2007). Metodoloía de investigación en las ciencias de la actividad física y el deporte: Ampliando horizontes. Recuperado de https://rua.ua.es/dspace/bitstream/10045/12270/1/blasco.pdf

Barros, P. (s.f.). Historia de los inventos. Recuperado de http://www.librosmaravillosos.com/inventos/pdf/Historia%20de%20los%20Inventos%20-%20Sucesos%20N%2012.pdf

Bruno, A., & Cabrera, N. (2006). La recta numérica en los libros de texto en España. Recuperado de http://www.redalyc.org/pdf/405/40518306.pdf

Camacho, J. (2016). Diseño de un software educativo educativo para el aprendizaje de operaciones con números enteros en las y los estudiantes de octavo año de educación general básica en la Institución educativa fiscal ”Pichincha”. Recuperado de http://www.dspace.uce.edu.ec/handle/25000/6249

Carrillo, J., Contreras, L., Climent, N., Montes, M., Escudero, D., & Flores, E. (2016). Didáctica de la matemáticas para maestros de educación primaria. Recuperado de https://books.google.com.co/books?id=GxJMDwAAQBAJ&lpg=PA64&dq=dificultad%20sumas%20de%20cantidades%20negativas&hl=es&pg=PR3]v=onepage&
q=dificultad%20sumas%20de%20cantidades%20negativas&f=false

Carrión, C. (2005). Discusiones necesarias entorno a la evaluación de la educación. Revista Mexicana de Investigación Educativa, 10 (27), 1259-1263. Recuperado de http://www.redalyc.org/pdf/140/14002718.pdf

Chaparro, O., Póveda, D., Fernández, R., Ministerio de Educación Nacional, & Universidad del Valle. (s.f.). Jugando con los números enteros. Recuperado de http://www.colombiaaprende.edu.co/html/mediateca/1607/articles-110453 archivo.pdf

Chehaybar, & Kuri. (2012). Técnicas para el aprendizaje grupal- grupos numerosos (4a ed.). Recuperado de http://132.248.192.241/editorial/wp-content/uploads/2014/10/T%C3%A9cnicas-de-aprendizaje-PDF.pdf

Cid, E. (s.f.). Obstáculos epistemológicos en la enseñanza de los números negativos. Recuperado de http://www.ugr.es/jgodino/siidm/cangas/Negativos.pdf

Colombia aprende, & Ministerio de educación Nacional. (s.f.). ¿Qué hay que saber de las competencias matemáticas? Recuperado de http://www.colombiaaprende.edu.co/html/home/1592/article-103987.html

Contreras, L. (1989). El concepto de número en preescolar. Recuperado de https://revistasuma.es/IMG/pdf/3/029-033.pdf

Corporación Universitaria del Caribe. (s.f.). Matemáticas aplicadas. Recuperado de file:///C:/Users/Cpe.Cpe-PC/Downloads/MATEMATICA%20APLICADA MATEMATICA%20APLICADA.pdf

Cubillos, A., & León, C. (2016, junio). El proyecto de aula: Una historia de por qué y para qué de los números enteros. VIDYA, 36(1), 43-52. Recuperado de https://www.periodicos.unifra.br/index.php/VIDYA/article/viewFile/567/1714

Díaz B, A., & Universidad Nacional Autónoma de México. (s.f.). Gu´ıa para la elaboración de una secuencia didáctica. Recuperado de http://www.setse.org.mx/ReformaEducativa/Rumbo%20a%20la%20Primera%2
0Evaluaci%C3%B3n/Factores%20de%20Evaluaci%C3%B3n/Pr%C3%A1ctica%20Profesional/Gu%C3%ADa-secuencias-didacticas_Angel%20D%C3%ADaz.pdf

Domínguez, E., Matos, R., Molina, C., & Gómez, I. (2011). El ABP mediado con tecnología móvil como estrategia pedagógica para el desarrollo de la competencia matemática en resolución de problemas: un caso con la adición de números enteros negativos. Zona Próxima. Universidad del Norte, 1 (14), 12-27. Recuperado de http://rcientificas.uninorte.edu.co/index.php/zona/article/viewArticle/3714/4734

Díaz, G. (2013). El trabajo colaborativo como estrategia de aprendizaje que produce aprendizaje significativo: Estudio de Caso de estudiantes de la carrera de Tecnología en Programación de Aplicaciones Web de la Universidad Autónoma de Bucaramanga. Recuperado de https://repositorio.itesm.mx/bitstream/handle/11285/619724/TESIS%20Gonzalo%20D%C3%ADaz%20C.pdf?sequence=1

Espada, B. (2017, 12 junio). Sistema de numeración Maya y números Mayas [Foto]. Recuperado 11 junio, 2018, de https://sobrehistoria.com/sistema-de-numeracion-maya-y-numeros-mayas

Gallardo, A., & Hernández, A. (s.f.). Emergencia de los números enteros. Recuperado de http://www.matedu.cinvestav.mx/maestriaedu/docs/asig5/Agallardo.pdf

García, L. (2011). Uso de Tecnología Informática en el Aprendizaje del Algebra con Números Enteros. Recuperado de https://repositorio.itesm.mx/bitstream/handle/11285/571150/DocsTec 12132.pdf?sequence=1

Gómez, B. (2001). “La justificación de la regla de los signos en los libros de texto: ¿Por qué menos por menos es más? In P. Gómez, & L. Rico (Eds.), Iniciación a la investigación en didáctica de la matemática (pp. 289-309). Recuperado de https://www.uv.es/gomezb/4Lajustificaciondeladeregla.pdf

González, M., Kaplan, J., Osua, G., & Reyes, M. (2010). La secuencia didáctica, herramienta pedagógica del modelo educativo ENFACE. Universidades, 1(46), 27-33.Recuperado de http://www.redalyc.org/pdf/373/37318636004.pdf

Guía para la elaboracón de la propuesta pedagógica. (s.f.). Recuperado 28 mayo, 2018, de http://faud.mdp.edu.ar/files/11 guia elaboracion propuesta pedagogica.pdf

Huamán, H. (2005). Manual de Técnicas de Investigación. Conceptos y aplicaciones. Recuperado de https://books.google.com.co/books?id=OEHABAAAQBAJ&lpg=
PA13&dq=observacion%20%20investigativo&hl=es&pg=PA3]v=onepage&q=observacion%20%20investigativo&f=false

Iriarte, M., Jimeno, M., & Vargas, I. (1991). Obstáculos en el aprendizaje de los números enteros. SUMA, 7, 13-18. Recuperado de http://funes.uniandes.edu.co/7868/

Maca, A. (2016). La enseñanza de los números enteros un asunto sin resolver en las aulas. Recuperado de http://ridum.umanizales.edu.co:8080/xmlui/bitstream/handle/6789/2640/
TRABAJO%20FINAL%20MAESTR%C3%8DA%20LA%20ENSE%C3%91ANZA%20DE%20LOS%20NUMEROS%20ENTEROS%20
UN%20ASUNTO%20SIN%20RESOLVER%20EN%20LAS%20AULAS.pdf?sequence=1&isAllowed=y

Madroñero, J. (2016). Guía de matemáticas elementales. Recuperado de http://www.digitaliapublishing.com.aure.unab.edu.co/a/47597/guia-de-matematicas-elementales

Masachs, A., Camprubí, G., & Naudi, M. (2005). El aprendizaje significativo en la resolución de problemas matemáticos. Recuperado de http://funes.uniandes.edu.co/2624/1/OlayaElvalorAsocolme2012.pdf

Maz, A. (2005). Los números negativos en España en los siglos XVIII y XIX. Recuperado de http://digibug.ugr.es/bitstream/handle/10481/556/15378184.pdf;jsessionid=BF732A
F0928CD91F91AAD73BA68C1653?sequence=1

Mazarío, I., Hernández, R., Lavin, M., Hortan, M., & Mazaríp, A. (2002). Reflexiones sobre un tema polémico: la resolución de problemas. Recuperado de http://libros.metabiblioteca.org/bitstream/001/358/5/978-959-16-0676-1.pdf

Ministerio de Educación Nacional. (s.f.). Estándares Básicos de Competencias en Matemáticas. Recuperado de https://www.mineducacion.gov.co/1621/articles-116042_archivo_pdf2.pdf

Ministerio de educación nacional. (1994, 8 febrero). Ley 115, ley general de educación. Recuperado de https://www.mineducacion.gov.co/1621/articles-85906 archivo_pdf.pdf

Ministerio de Educación Nacional. (2016). Derechos Básicos de aprendizaje matemáticas. Recuperado de http://aprende.colombiaaprende.edu.co/siemprediae/93226

Molina, S. (2005). Los conocimientos previos de los estudiantes de tercer curso de Magisterio acerca de la Organización Escolar: implicaciones para la docencia universitaria. Recuperado de https://dialnet.unirioja.es/descarga/articulo/2044872.pdf

Mónaco, N. (2009). Matemática e historia. El número cero. Recuperado de file:///C:/Users/Cpe.Cpe-PC/Downloads/Dialnet-MatematicaEHistoria-3045279.pdf

Moreira, M., Caballero, M., & Rodríguez, M. (Eds.). (1997). Aprendizaje significativo: un concepto subyacente (-). Recuperado de https://www.if.ufrgs.br/_moreira/apsigsubesp.pdf

Mucía, J. (1996). Filosofía de los números Mayas [Foto]. Recuperado 10 junio, 2018, de http://mysticomaya.com/a_05_aut/Filosofiade los numeros mayas_esp.pdf

Números negativos [Foto]. (s.f.). Recuperado de http://numerosnegativos.wikispaces.com/file/view/recta 1.GIF/172001649/773x232/recta_1.GIF

Olaya, L. F., & Forigua, J. E. (2012). El valor absoluto: una mirada desde la metodología de la ingeniería didáctica. In G. Obando (Ed.), Memorias del 13er Encuentro Colombiano de Matemática Educativa (pp. 460-465). Recuperado de http://funes.uniandes.edu.co/2624/

Oteyza, E., Lam, E., Hernández, C., Carrillo, A., & Ramírez, A. (2001). Geometría analítica y Trigonométrica. Recuperado de https://books.google.com.co/books?id=4bHgbXfpDrkC&lpg=PA3&dq=inverso%2
0aditivo&hl=es&pg=PP1]v=onepage&q=inverso%20aditivo&f=false

Pérez, A. (2016). Análisis de los números enteros en el tercer ciclo de educación primaria. Comparación entre dos libros de dicha etapa. Recuperado de file:///C:/Users/Cpe.Cpe-PC/Downloads/Prez_Osorio_Antonio_TFG_EducacinPrimaria.pdf

Pérez, M., & Roa, C. (2010). Herramientas para la vida: Hablar, Leer y Escribir para comprender el mundo. Recuperado de http://repositoriosed.educacionbogota.edu.co/jspui/bitstream/123456789/100/1/referenteslenguajeciclo1.pdf

Pluvinage, F., & Flores, P. (2016). Génesis Semiótica de los Enteros. Bolema: Boletim de Educação Matemática, 30 (54), 120-141. Recuperado de http://www.scielo.br/scielo.php?script=sciarttext&pid=S0103-636X2016000100120&lng=es&tlng=es

Psicología educativa y la labor docente. (s.f.). Recuperado 27 mayo, 2018, de file:///C:/Users/Estudiante/AppData/Local/Temp/Temp2_tesis_modelo.zip/3.%20tesis%20tamgran%20geoplano.pdf

Ramírez París, X. (2009, 10 julio). La lúdica en el aprendizaje de las matemáticas. Zona próxima, 10(1), 140-145. Recuperado de http://www.redalyc.org/pdf/853/85312281009.pdf

Rodríguez, M. (2010). La teoría del aprendizaje significativo en la perspectiva de la psicología cognitiva. Barcelona, España: Octaedro.

Rodríguez, R. (2013). Conjuntos numéricos estructuras algebraicas y fundamentos de álgebra lineal. Madrid, España: TEBAR FLORES, S.L...

Rodríguez, R. (2013). Matemáticas I: Conjuntos numéricos, estructuras algebraicas y fundamentos de álgebra lineal. Volumen II: Estructuras algebraicas y fundamentos de álgebra lineal. Madrid, España: Tébar.

Rojas, J., & Ariza, A. (2013). Propuesta didáctica para la enseñanza de los números enteros1. Revista Científica. Universidad Distrital Francisco José de Caldas, 1, 542-545. Recuperado de http://funes.uniandes.edu.co/6706/1/Ariza2012Propuesta.pdf

Ruiz, G. (2013). Orden de los números naturales. Recuperado de http://webcache.googleusercontent.com/search?q=cache:rt-lpPd2D2IJ:www.fumtep.edu.uy/index.php/didactica/item/
download/8965d07f949af50235d25b850d8b804bfc7+&cd=1&hl=es&ct=clnk&gl=co

Sánchez, H., Parcero, R., Romo, L., Becerra, E., & Goytia, K. (2001). Historia Universal (Ed. rev.). Recuperado de https://books.google.com.co/books?id=YyMfRyEc2ZEC&lpg=PA8&dq=etapas%2
0de%20la%20historia%20antigua%20moderna&hl=es&pg=PP1]v=onepage&q=etapas%20de%20la%20historia%20antig
ua%20moderna&f=false

Sánchez, O. (2012). Propuesta didáctica para la enseñanza de (Z, +,) a estudiantes de séptimo grado. Recuperado de http://recursosbiblioteca.utp.edu.co/tesisd/textoyanexos/510712S211.pdf

Santiago, A., & Santiago, M. (2011). Resúmenes de matemáticas I con notas históricas. Recuperado de https://books.google.com.co/books?id=P8UbiqT87EMC&printsec=frontcover&hl=es]v=onepage&q&f=false

Velasco, J., Rojas, L., & Gallardo, Y. (s.f.). Matemáticas 7◦ grado. Recuperado de https://edwinnieves.files.wordpress.com/2009/11/matematicas-7.pdf

Velez, D., & Varela, O. (2014). El descubrimiento de los números negativos.

Número de la obra: 31

Título: Chiva “El Lucerito”

Autora: Margarita Chávarro Castro

Lugar: Municipio La Plata, Huila

Fecha de captura: Abril de 2013

Técnica: Fotografía digital

Fuente: Colección Margarita Chávarro Castro